带电粒子在磁场中做圆周运动的磁场种类

福建 连彬星

带电粒子在磁场中的运动问题是高考的热点与难点，对考生的空间想象能力、作图能力、物理过程分析能力以及物理规律的综合应用能力都有很高的要求。不仅涉及动力学知识，还要用到数学平面几何中的解析几何知识。本类题目通常为大的计算题，分值大，难度大，必须处理好。难点之一，就是如何画出运动轨迹，如何找到圆心，如何找到旋转半径与已知长度、角度的数量关系。难点之二，就是极限条件的取得。本文就五种常见的磁场种类可能出现的临界问题进行整理归类，供大家参考。

一、单边界磁场

【例1】如图1所示S为电子射线源，能在图示纸面上和360°范围内向各个方向发射速率相等的质量为m、带电-e的电子，MN是一块足够大的竖直挡板且与S的水平距离OS=L，挡板左侧充满垂直纸面向里的匀强磁场；①若电子的发射速率为v0，要使电子一定能经过点O，则磁场的磁感应强度B的条件？②若磁场的磁感应强度为B，要使S发射出的电子能到达挡板，则电子的发射速率多大？③若磁场的磁感应强度为B，从S发射出的电子的速度为meBL2，则挡板上出现电子的范围多大？

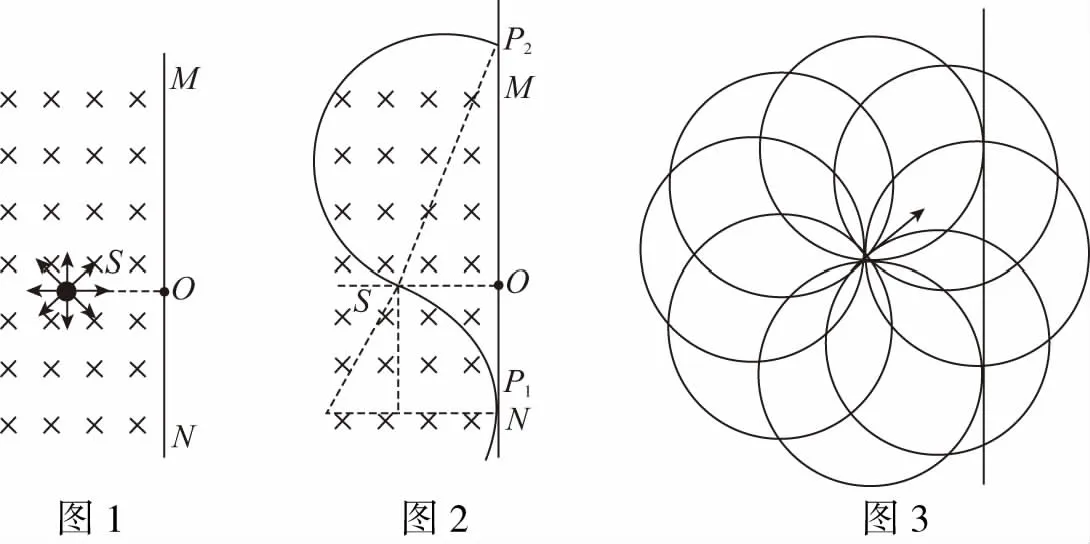
【解析】电子从点S发出后受到洛伦兹力作用做匀速圆周运动，由于电子从点S射出的方向不同将使其受洛伦兹力方向不同，导致电子的轨迹不同，过射出点作速度的垂线—半径垂直于速度(速度沿圆的切线方向)，试着把8个对称方向射出的粒子轨迹工工整整画出来，如图3所示，分析知只有从点S向与SO成锐角且位于SO上方发射出的电子才可能经过点O。由于粒子从同一点向各个方向发射，粒子的轨迹构成绕S点旋转的动态圆，动态圆的每一个圆都是顺时针旋转，这样可以作出打到最高点与最低点的轨迹，如图2所示，最低点为动态圆与MN相切时的交点，最高点为动态圆与MN相割，且SP2为直径时的交点，P2为最高点。

本题利用了动态圆法寻找满足范围的“临界轨迹”及“临界半径R0”，然后利用粒子运动的实际轨道半径R与R0的大小关系确定范围。

二、双边界磁场

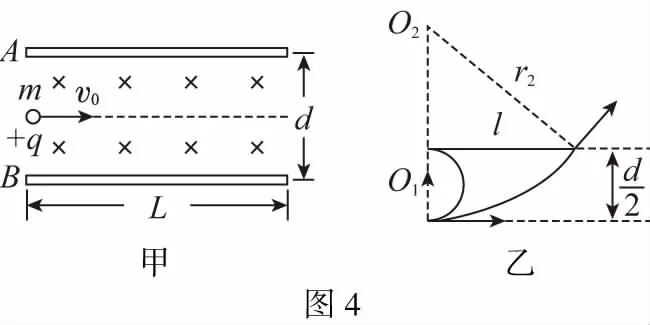
【例2】如图4甲所示，A、B为一对平行板，板长为L，两板距离为d，板间区域内充满着匀强磁场，磁感应强度大小为B，方向垂直纸面向里，一个质量为m，带电量为+q的带电粒子以初速度v0，从A、B两板的中间，沿垂直于磁感线的方向射入磁场。求在什么范围内，粒子能从磁场内射出？

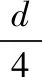
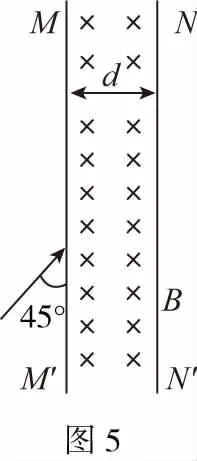
【例3】如图5所示，宽度为d的有界匀强磁场，磁感应强度为B，MM′和NN′是它的两条边界。现有质量为m，电荷量为q的带电粒子沿图示方向垂直磁场射入。要使粒子不能从边界NN′射出，则粒子入射速率v的最大值是多少？

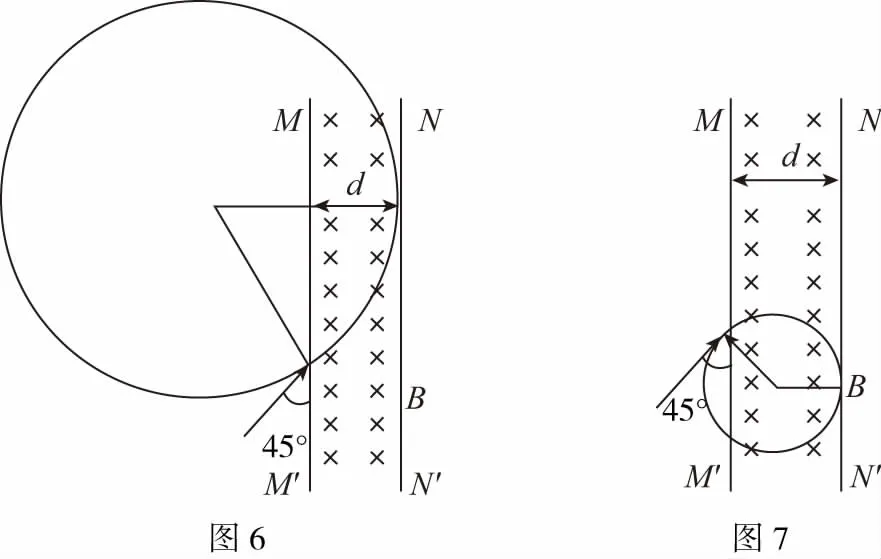
【解析】粒子射入磁场后受到洛伦兹力的作用，将做匀速圆周运动，但是没有说明是正电荷还是负电荷，所以会有向两个方向偏转的可能。过入射点作速度的垂线—半径垂直于速度(速度沿圆的切线方向)，圆周运动的圆心在入射点的左上方(图6)和右下方(图7)。要想使粒子不从NN′射出，两种情况下半径r都必须小于某个值。利用数形结合可以得到两种情况下的临界半径大小，通过半径和速度的关系，从而得到速度的最大值。

三、圆形边界磁场

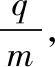
(1)粒子沿环状的半径方向射入磁场，不能穿越磁场的最大速度；

(2)所有粒子不能穿越磁场的最大速度。

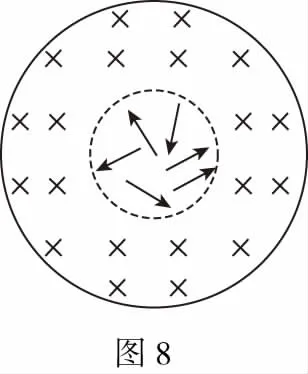
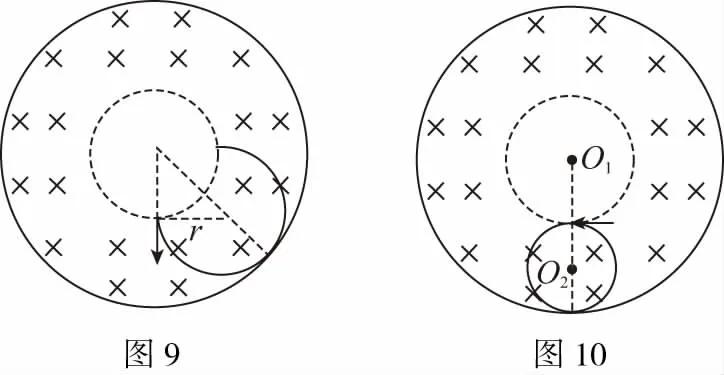
【解析】本题属于临界类问题，寻求“临界轨迹”是解题的关键。要粒子沿环状的半径方向射入磁场，不能穿越磁场，则粒子的临界轨迹必须要与外圆相切(图9)；要使所有粒子都不穿越磁场，应保证沿内圆切线方向射出的粒子不穿越磁场，即运动轨迹与内、外圆均相切(图10)。

四、三角形边界磁场

【例5】如图11所示，左边有一对平行金属板，两板的距离为d，电压为U，两板间有匀强磁场，磁感应强度为B0，方向平行于板面并垂直纸面朝里。图中右边有一边长为a的正三角形区域EFG(EF边与金属板垂直)，在此区域内及其边界上也有匀强磁场，磁感应强度大小为B，方向垂直纸面向里。假设一系列电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入金属板之间，沿同一方向射出金属板间的区域，并经EF边中点H射入磁场区域，不计重力。已知这些离子中的离子甲到达边界EG后，从边界EF穿出磁场，求离子甲的质量。

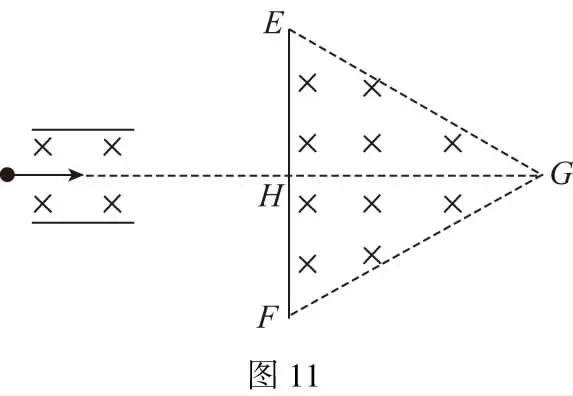
【解析】本题也属于临界类问题，寻求“临界轨迹”是解题的关键。要粒子垂直EF中点方向射入磁场，不能穿出EG边，则粒子的临界轨迹必须要与EG边相切，再回到EF边。过进入点作速度的垂线—半径垂直于速度(速度沿圆的切线方向)，圆心在EH上，圆心到HG的距离和EG的距离要相等(图12)。

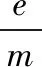
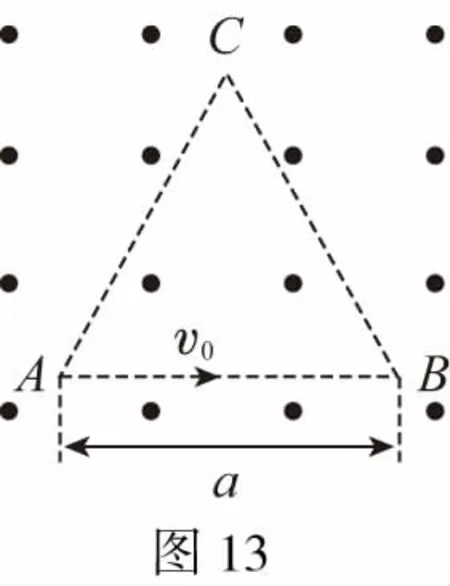
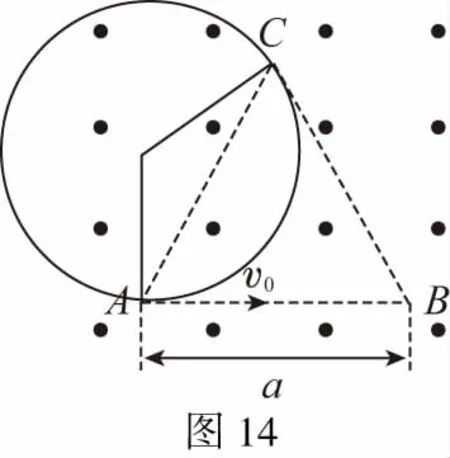
【解析】本题也属于临界类问题，寻求“临界轨迹”是解题的关键。电子进入磁场后会向上偏转做圆周运动，磁感应强度越大，运动轨迹半径越小。电子从C点离开时运动轨迹半径最小，即磁感应强度最大。作AB边的垂线和BC边的垂线，两者相交于一点即为轨迹圆心(图14)，通过角度关系可求出临界半径，然后得到磁感应强度的大小。

五、未知边界磁场

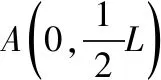
(1)匀强电场的电场强度E的大小；

(2)匀强磁场的磁感应强度B的大小和电子在磁场中运动的时间t；

(3)矩形有界匀强磁场区域的最小面积Smin。

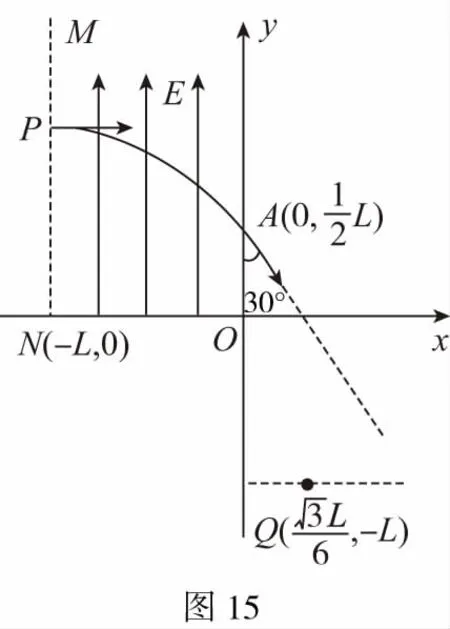
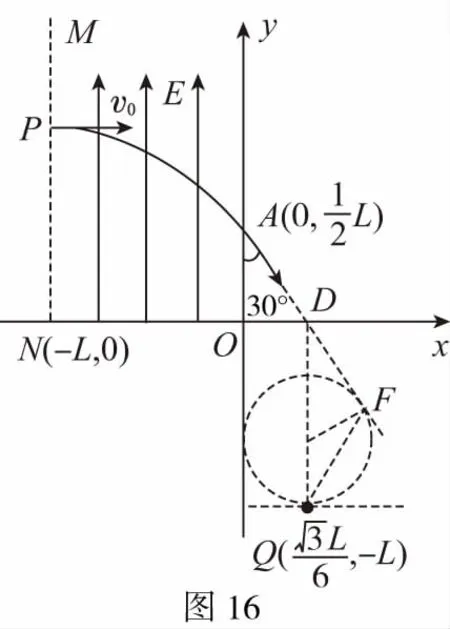
【解析】(1)设电子在电场中运动的加速度大小为a，时间为t，离开电场时，沿y轴方向的速度大小为vy。

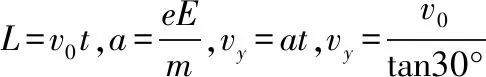
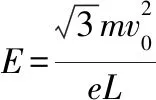
(2)设轨迹与x轴的交点为D，O、D间的距离为xD，则

所以DQ平行于y轴，电子在磁场中做匀速圆周运动的轨迹圆心在DQ上，电子运动轨迹如图16所示。设电子离开电场时速度大小为v，在磁场中做匀速圆周运动的轨迹半径为r，周期为T。

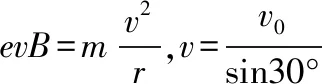
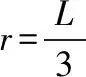
电子在磁场中偏转的角度为120°

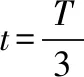
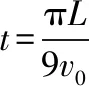
(3)以切点F、Q的连线为矩形的一条边，与电子的运动轨迹相切的另一边作为FQ的对边，此时有界匀强磁场区域面积最小

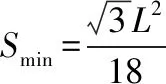
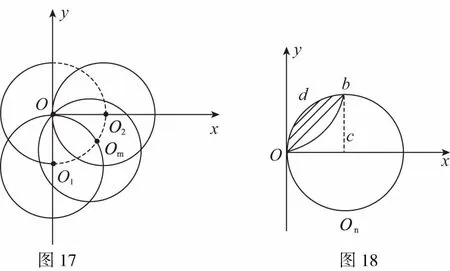
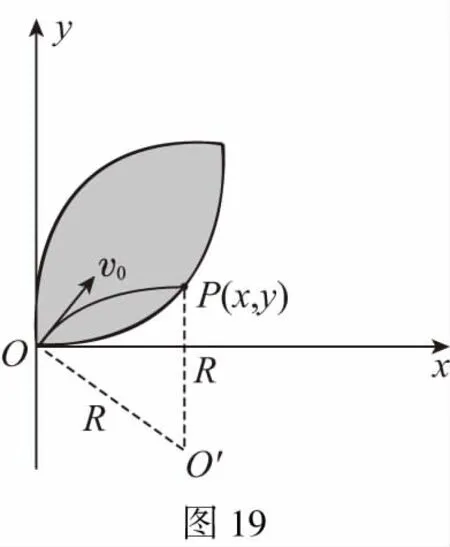
【例8】在xOy平面内有许多电子(质量为m、电荷量为e)，从O点不断以相同速率v0沿不同方向射入第一象限。现加一个垂直于xOy平面向内、磁感强度为B的匀强磁场，要求这些电子穿过磁场后都能平行于x轴向x正方向运动，求符合该条件磁场的最小面积。

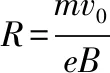
【总结】这类问题的解题步骤可归纳为：

(1)明确轨迹。带电粒子在磁场中的运动为圆周运动，需要首先确定好运动轨迹。有些情境是没有明确告诉轨迹的，需要分析、画图(草图)，有时候画出来图还要经过修改。一般过进入点作速度的垂线，半径垂直于速度(速度沿圆的切线方向)或者作进出点连线的中垂线。

(2)找圆心。确定了大致的运动轨迹后找圆心。圆心一般是两个点的速度的垂线交点。

(3)数形结合。结合题意条件，求出偏转半径R。