都是细绳惹的“祸”
2019-04-24重庆杨天才
重庆 杨天才
细绳是应用广泛的一种工具,以其为素材的问题,在历年高考物理题中都有体现,也是广大考生的难点。细绳按不同标准有不同的分类,按有无质量可分为轻绳和有质量的绳;轻绳按有无约束,可分为自由绳和约束绳;约束绳按约束方式可分为滑轮约束和结点约束;从受力角度看,轻绳所处的状态可分为松弛(FT=0)、绷直(FT≥0)、绷紧(FT>0)、断裂(拉力从较大突变为零)。在不同分类里,与绳相连的物体的受力情况、运动情况有不同的特点,现举例归纳如下。
一、同一轻绳各处的张力大小均相等
(1)若轻绳上有“活结”,如滑轮、光滑挂钩,“活结”把绳子分成两段,但可以沿绳子移动。实际上是同一根绳,所以由“活结”分开的两段绳子上张力的大小一定相等。
(2)若轻绳上有“死结”,“死结”把绳子分成两段,且不可以沿绳子移动。两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力大小不一定相等。
【例1】如图1甲所示,细绳AD跨过固定的水平轻杆BC右端的定滑轮,挂住一个质量为M1的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°夹角,轻杆的G点用细绳GF拉住一个质量为M2的物体,求:
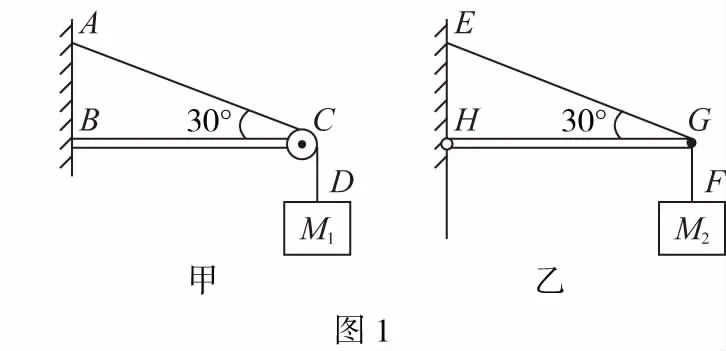
(1)细绳AC段的张力FTAC与细绳EG的张力FTEG之比;
(2)轻杆BC对C端的支持力;
(3)轻杆HG对G端的支持力。
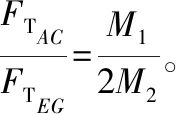
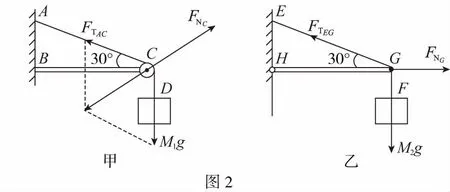
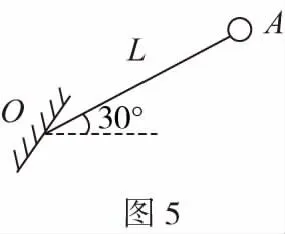
(2)图2甲中,三个力之间的夹角都为120°,根据平衡条件有FNC=FTAC=M1g,方向与水平方向成30°夹角,指向右上方。
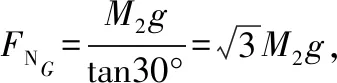
二、轻绳两端连接的物体沿绳方向速度大小相等,方向不同
【例2】(多选)如图3所示,做匀速直线运动的小车A通过一根绕过定滑轮的长绳吊起一重物B,设重物和小车速度的大小分别为vB、vA,则
( )
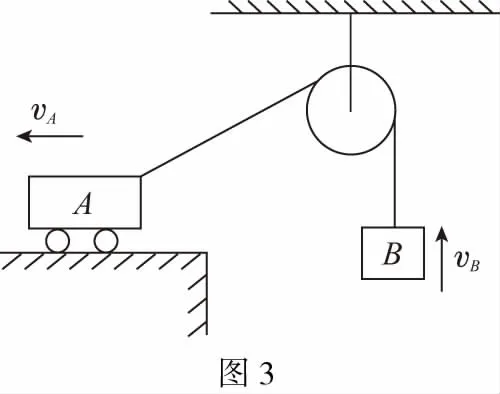
A.vA>vB
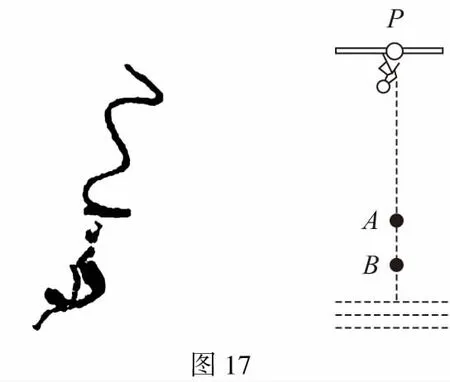
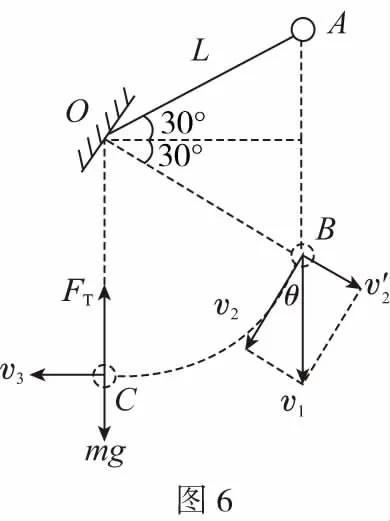
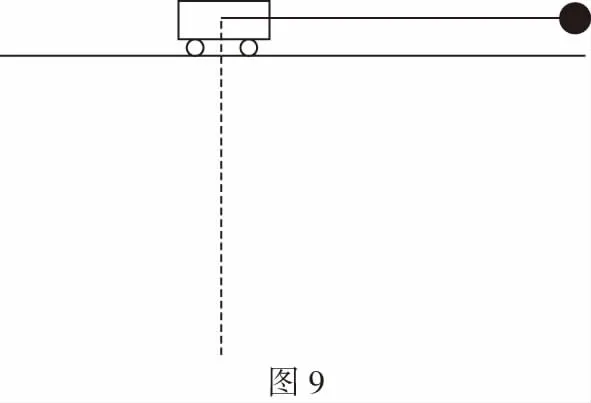
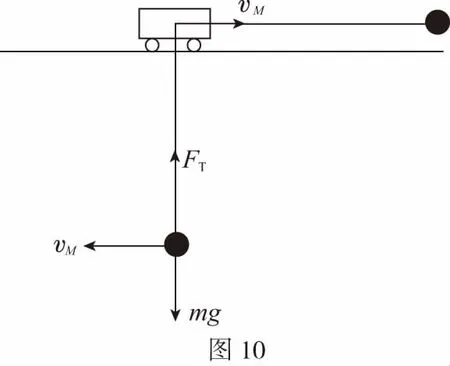
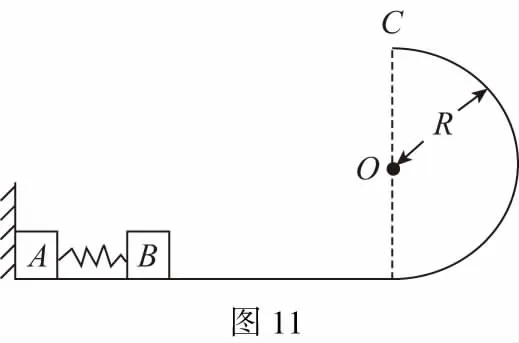
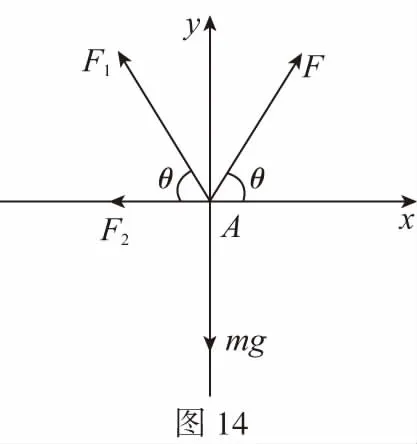
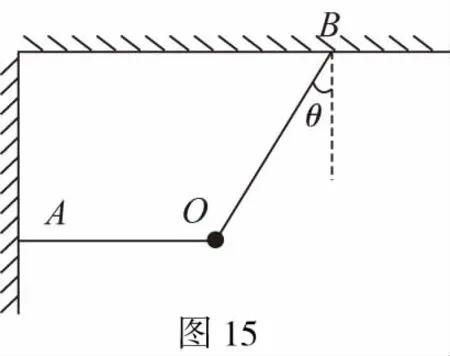
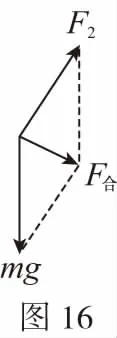
B.vA C.绳的拉力等于B的重力 D.绳的拉力大于B的重力 【解析】小车A向左运动的过程中,小车的速度是合速度,可分解为沿绳方向与垂直于绳方向的速度,如图4所示,轻绳两端连接的物体沿绳方向速度大小相等。由图可知vB=vAcosθ,则vB 1.绳端两物体共速为零 【例3】如图5所示,将一质量为m的小球用长为L的轻绳系住,绳的另一端固定在天花板上O点,现让绳子刚好绷直且与水平方向成30°夹角,松手释放后,求小球运动到最低点时绳的拉力大小。 v2=v1cos30° 从B到C,由机械能守恒定律,有 在C点,对m由合外力提供向心力,有 2.绳端两物体共速且不为零 3.定滑轮约束轻绳后,绳端两物体速度大小相等方向相反 【例5】(2017年天津卷第10题)如图8,物块A和B通过一根轻质不可伸长的细绳连接,跨放在质量不计的光滑定滑轮两侧,质量分别为mA=2 kg、mB=1 kg。初始时A静止于水平地面上,B悬于空中。先将B竖直向上再举高h=1.8 m(未触及滑轮)然后由静止释放。一段时间后细绳绷直,A、B以大小相等的速度一起运动,之后B恰好可以和地面接触。取g=10 m/s2。空气阻力不计。求: (1)B从释放到细绳刚绷直时的运动时间t; (2)A的最大速度v的大小; (3)初始时B离地面的高度H。 (2)设细绳绷直瞬间B速度大小为v0,有v0=gt=6 m/s,细绳绷直瞬间,细绳张力远大于A、B的重力,总动量守恒:mBv0=(mA+mB)v,绳子绷直瞬间,A、B系统获得的速度:v=2 m/s,之后A做匀减速运动,所以A的最大速度为2 m/s; 4.轻绳自由移动,绳端两物体满足动量守恒和机械能守恒。 【例6】如图9,质量为M的小车放在光滑的轨道上,长为L的轻绳一端系在小车上另一端拴一质量为m的金属球,将小球拉开至轻绳处于水平状态由静止释放。求: (1)小球摆动到最低点时两者的速度; (2)此时小球受细绳的拉力是多少。 【解析】(1)由动量守恒定律0=mvm-MvM (2)当小球运动到最低点时,受到竖直向上的拉力FT和重力作用如图10,根据向心力的公式 【例7】光滑水平面上放着质量mA=1 kg的物块A与质量mB=2 kg的物块B,A与B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接),用手挡住B不动,此时弹簧弹性势能Ep=49 J。在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图11所示。放手后B向右运动,绳在短暂时间内被拉断,之后B冲上与水平面相切的竖直半圆光滑轨道,其半径R=0.5 m,B恰能到达最高点C。g=10 m/s2,求: (1)绳拉断后瞬间B的速度vB的大小; (2)绳拉断过程绳对B的冲量I的大小; (3)绳拉断过程绳对A所做的功W。 【解析】(1)设B在绳被拉断后瞬间的速度为vB,到达C点时的速度为vC,有 代入数据得vB=5 m/s。 代入数据得I=-4 N·s,其大小为4 N·s。 (3)设绳断后A的速度为vA,取水平向右为正方向,有 代入数据得:W=8 J。 【例8】(多选)如图12所示,一根长度为2L、质量为m的绳子挂在定滑轮的两侧,左右两边绳子的长度相等。绳子的质量分布均匀,滑轮的质量和大小均忽略不计,不计一切摩擦。由于轻微扰动,右侧绳从静止开始竖直下降,当它向下运动的位移为x时,加速度大小为a,滑轮对天花板的拉力为FT,绳子动能为Ek。已知重力加速度大小为g,下列a-x、Ek-x、FT-x关系图线正确的是 ( ) 【例9】物体A的质量为2 kg,两根轻细绳b和c的一端连接于竖直墙上,另一端系于物体A上,在物体A上另施加一个方向与水平线成θ角的拉力F,相关几何关系如图13所示,θ=60°。若要使两绳都能伸直,求拉力F的大小范围。(g取10 m/s2) 【解析】作出物体A的受力分析图如图14所示,由平衡条件得 Fsinθ+F1sinθ-mg=0 Fcosθ-F2-F1cosθ=0 要使两绳都伸直,则有F1≥0,F2≥0 【例10】如图15所示,一质量为m的物体系于长度分别为L1、L2的两根细绳OA、OB上,OB一端悬挂在天花板上,与竖直方向夹角为θ,OA水平拉直,物体处于平衡状态,现在将OA剪断,求剪断瞬间物体的加速度。 【解析】剪断瞬间,绳OA产生的拉力F1消失,对绳来说,其伸长量很微小,可以忽略不计,不需要形变恢复时间,因此,绳子中的张力也立即发生变化,这时F2将发生瞬时变化,mg与F2的合力将不再沿水平方向,而是沿小球下一时刻做单摆运动的圆弧的切线方向,与绳垂直,如图16所示,F合=mgsinθ,所以a=gsinθ。 【例11】蹦极是一项既惊险又刺激的运动,深受年轻人的喜爱。如图17所示,蹦极者从P点由静止跳下,到达A处时弹性绳刚好伸直,继续下降到最低点B处,B离水面还有数米距离。蹦极者(视为质点)在其下降的整个过程中,重力势能的减少量为ΔE1,绳的弹性势能的增加量为ΔE2,克服空气阻力做的功为W,则下列说法正确的是 ( ) A.蹦极者从P到B的运动过程中,速度一直增大 B.蹦极者与绳组成的系统从A到B的运动过程中,机械能守恒 C.ΔE1=W+ΔE2 D.ΔE1+ΔE2=W 【解析】蹦极者下降过程中,速度先增大后减小,A错误;由于空气阻力做功,故机械能减少,B错误;由功能关系得W=ΔE1-ΔE2,解得ΔE1=W+ΔE2,C正确,D错误。 综上所述,细绳在高中物理试题中扮演着重要的角色,理清不同细绳的特点,具体问题具体分析是解题的关键。对一端松弛,仅另一端连接物体的轻绳,绳中受力为零不再举例。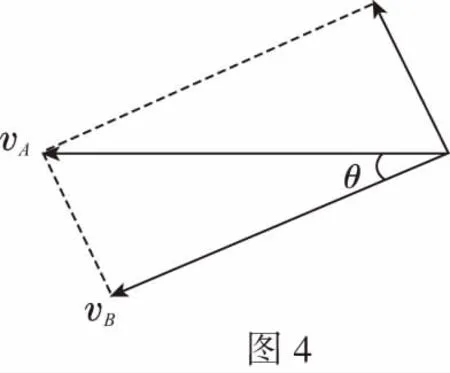
三、绳绷紧,轻绳两端沿绳方向连接的物体瞬间达到共速,此时满足动量守恒,一般机械能有损失
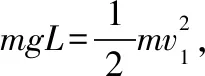
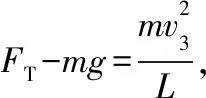
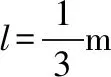
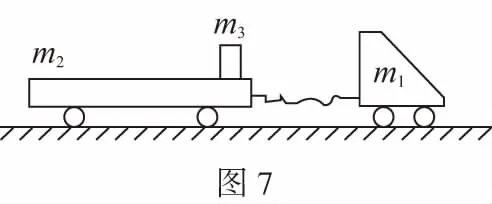
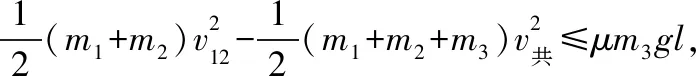
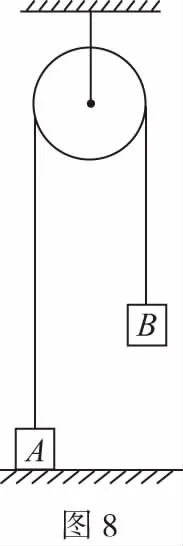
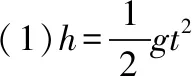
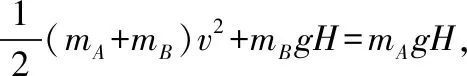
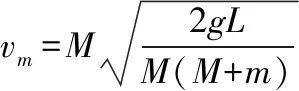
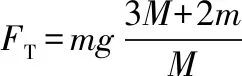
四、绳拉断,轻绳两端沿绳方向连接的物体速度不一定相等,此时满足动量守恒,机械能有损失
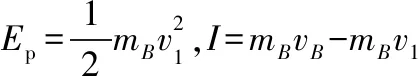
五、有质量的绳不再满足上述轻绳的系列结论,因研究对象会随着绳长的改变而发生改变
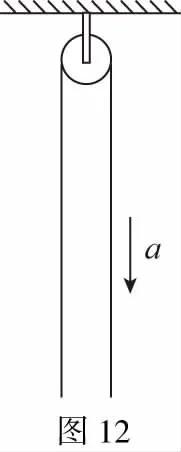
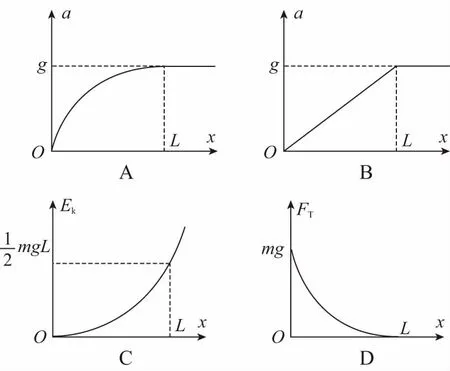
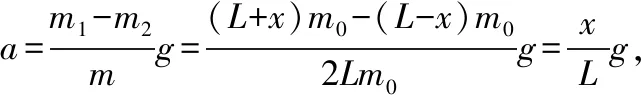
六、轻绳中张力的大小随状态不同而改变
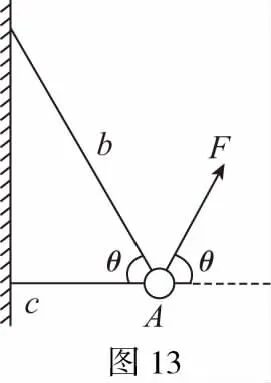
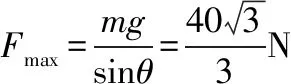
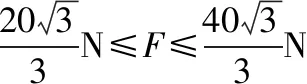
七、轻绳中张力的大小发生突变
八、弹性轻绳等效于轻弹簧,受力时发生明显的弹性形变