挖掘习题内涵提升训练价值

苗培林

在苏教版教材六年级下学期总复习《图形与几何》单元中有这样一道习题：

在备课时，笔者经过精心解读习题，挖掘其内涵，对这道习题进行了四个层次的处理，最终提升了这道习题的思维训练价值，对思想方法进行了有效渗透，现将这道习题的设计与思考加以整理与同行共享。

第一层次：删除增加，寓练习于探索实践之中。

分别出示第一组题目：

（1）如图1，在一块边长6厘米的正方形纸上画一个最大的圆。这个圆的面积是多少平方厘米？这个圆的面积占正方形面积的百分之几？

（2）如图1，在一块边长4厘米的正方形纸上画一个最大的圆。这个圆的面积占正方形面积的百分之几？

（3）如图1，在一块边长10厘米的正方形纸上画一个最大的圆。这个圆的面积占正方形面积的百分之几？

学生计算并交流。

师：比较这一组题目，你发现了什么？

图1

生1：圆的面积占正方形面积的78.5%。

生2：生1的话不完全正确，应加一个前提，在正方形里画一个最大的圆，否则结论就不能成立。

生3：我来总结，在正方形里画一个最大的圆，圆的面积占正方形面积的78.5%。

分别出示第二组题目：(只列式不计算)

（1）如图2，已知正方形的面积是20平方厘米。求圆的面积。

（2）如图3，已知圆的面积是28.26平方厘米。求正方形的面积。

（3）如图4，已知正方形的面积是20平方厘米。求涂色部分的面积。

（4）如图5，已知正方形的面积是20平方厘米。求涂色部分的面积。

（5）如图6，已知正方形的面积是20平方厘米。求涂色部分的面积。

（6）如图7，已知正方形的面积是20平方厘米。求涂色部分的面积。

图2

图3

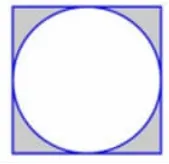
图4

图5

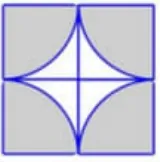
图6

图7

学生列式并说理由。

删除“圆的半径各是多少厘米”，基于以下三点考虑：一是学生在五年级学习《圆》单元时对这个最基本的知识点已经熟练掌握；二是在六年级复习《图形与几何》时已经对这个概念进行了再复习；三是在刚才计算圆的面积时也用到了这个知识。

增加两组习题，因为如果按照教材来实施的话，对学生来说思维跨度比较大，不能深刻理解。增加第一组习题，让学生经历探索，不完全归纳出“在正方形里画一个最大的圆，圆的面积占正方形面积的78.5%”。随后再增加一组变式练习，使学生及时对这一结论进行巩固和内化。这样处理就能寓练习于探索实践中，使学生做到探索与复习、知识与技能的有机融合，顺利达成知识建构。

第二层次：整体推进，聚练习于思维递进之中。

分别出示第三组题目：(只列式不计算)

（1）如图8，已知正方形的面积是20平方厘米。求涂色部分的面积。

（2）如图9，已知正方形的面积是20平方厘米。求涂色部分的面积。

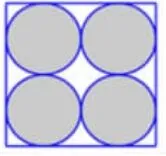
图8

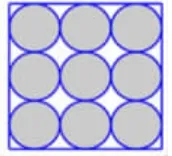
图9

学生列式并说理由。

师：从正方形里画1个最大的圆，到正方形里画4、9个完全一样的圆，那么接下来可能在正方形里画几个完全一样的圆？

生1：正方形里可以画16个完全一样的圆。

生2：正方形里可以画25个完全一样的圆。

师：为什么呢？

生3：其实是有规律可寻的：1 是 12，4 是 22，9 是 32，所以接下来是 42、52、……

师：除了这个外，再看看做的过程，你还发现了什么？

生4：我还发现所有圆的面积之和也是这个正方形面积的78.5%。

生5：我也是这么认为的。因为在正方形里画几个完全一样的圆，可以当作把正方形平均分成几个小正方形，小圆的面积就占小正方形面积的78.5%，那么所有圆的面积之和占大正方形面积的78.5%。

有了前面的铺垫，学生初步建成了“在正方形里画一个最大的圆，圆的面积占正方形面积的78.5%”这个模型，其实这个模型的内涵远远不止于此。笔者出示了教材所呈现的一组探索练习，这组练习又比前面的习题整体推进了一步，让学生以积极的心态，根据刚才探索的规律和积累的经验，尝试解决新问题，同化新知识，并建构新模型，思维得到了递进，创新能力得以培养。

第三层次：回顾反思，蕴练习于思想方法之中。

师：同学们，我们刚才做的题目其实就是数学课本第91页第11题。

学生仔细翻看课本上的这道练习题。

师：我们又是怎么做这道习题的？

（教师依次出示下面图形，帮学生回顾刚才做这几组题目的过程）

师：对你的复习，有什么启发？

生1：做题目的时候，不能只看表面，要深入思考。

生2：要会举一反三。

生3：要把题目做“厚”。

复习的目的是巩固所学的知识，形成技能，这只是浅层次的，更重要的是让学生在教师的引领下学会自我复习。“授人以鱼不如授人以渔”，教人知识，不如教人学会得到知识的方法。笔者让学生先看教材上这道习题，再一起回顾课堂上做这几组习题的过程，通过鲜明的对比让学生强烈地感受到原来这道习题还可以这样处理。然后面对教师的提问“对你的复习，有什么启发？”学生恍然大悟，觉得自己以后在复习、做练习的过程中也可以像老师这样，实现复习的自我拓展、自我发现、自我构建和自我反思，将复习知识技能转化成思想方法指导。如果只进行单纯的知识教学，学到的知识会随着时间的推移而遗忘，而方法的掌握、思想的形成，才能使学生受益终生。

第四层次：拓展提升，融练习于知识整合之中。

师：如果让你接着刚才的题目继续往下想，你还会想到什么？

学生独立思考。如果想不出来，教师可出示下面一两道题目启发学生思考。

（1）如图 10，已知正方形的面积是20平方厘米。求圆的面积。

（2）如图 11，已知长方形的面积是20平方厘米。求涂色部分的面积。

（3）如图 12，一个底面是正方形的长方体，高为10厘米，底面正方形边长为5厘米。如果把它削成最大的圆柱。求圆柱的体积。

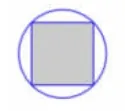
图10

图11

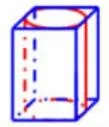
图12

通过前面三个层次的练习，看似结束，其实不然，这只是刚刚开始，为了使学生的思维向深度和宽度发展，整合知识，笔者最后抛出一个问题“如果让你接着刚才的题目继续往下想，你还会想到什么？”这一启发就可能一下子把学生的思路打开，他们可能会由“在正方形里画一个最大的圆”联想到“在圆里画一个最大的正方形”，由正方形联想到长方形、三角形等平面图形，由平面图形联想到立体图形等等。这些联想，看似偏离了教材原本的要求，但正是这种有意的偏离，才使得这一习题内在的思维价值充分彰显，学生的数学思维能力得到了很好的提升。

习题的设计，既要考虑巩固知识、形成技能的短期效应，还要在尊重数学知识本质的前提下，从完善学生的认知能力出发，从培养学生的思维能力出发，有意识地对习题内涵进行挖掘，把习题变“厚”，“借题发挥”，促进习题的功能最大化。