培养探究意识提升核心素养
——《包装的学问》教学设计与思考(二)
2019-04-22章莉莉
章莉莉
【教学内容】
北师大版五年级下册第80、81页。
【教学过程】
一、激发兴趣,导入新课
1.场景引入:课件出示几幅生活中包装的图片。(有单盒包装的图片,也有多盒拼装的图片)
师:看了生活中的包装后你有何感受?
2.定格单盒包装的图片,理解包装的含义。
师:包装纸包了盒子的哪些部分?
预设:表面。
师:求包装纸的大小就是求什么?
预设:表面积。
师:物品经过包装,显得更精美,可包装的目的不仅如此,在包装中还有许多学问,今天我们就来学习《包装的学问》。(板书课题)
【设计意图:通过欣赏图片,理解包装的含义。这样引入既可以让学生感受到包装给人们生活带来的便利,又拉近了数学与生活的距离,还为课堂学习营造了良好的氛围。】
二、动手操作,探究方案
●探究活动一:包装两盒糖果。
1.出示例题,明确包装意义。
师:再过几天就是六一儿童节,淘气要给台湾的小朋友寄糖果,两盒同样的糖果包成一包,怎样包才能节约包装纸?(一盒糖果长20cm、宽15cm、高5cm,接口处不计)
师:根据数据,说说哪个是大面?哪个是中面?哪个是小面?
2.动手操作,探究包装方案。
师:两盒糖果能有几种不同的包装?
(学生独立摆一摆,之后上台展示三种不同的包装方案)

3.计算比较,验证猜想。
(1)观察比较,猜想最节约包装纸的方案。
预设:第一种包装方案最节约。
师:多数同学都觉得第一种方案最节约包装纸,怎样验证?
预设:计算三种包装方案的表面积。
(2)计算验证。
师:观察图形特点,用自己喜欢的方法来计算,验证你的猜想。
请学生交流解题思路,预设∶
①根据包装后的长方体的长、宽、高计算。
②两个长方体表面积之和,减去重合面的面积就是现在的表面积。
③包装后10个长方形面积之和。

(3)小结。
验证和猜想一致,确实是第一种方案最节约。
师:为什么第一种包装方案最节约纸?
预设:包装方案有三种,其中最大的面重合,重合的面积越大,剩下表面积越小,越节约包装纸。通过计算比较得出结论:计算方法一、二简单实用。
【设计意图:两个长方体的包装方案是本课教学的重点,也是多个长方体拼摆的基础,分两个层次进行:先研究包装方案的多样化,再估一估、算一算,探究如何节约包装纸。三种计算方法都预设了,学生不一定都出现,课堂随机而动。计算验证猜想科学严谨,让学生在动手操作、观察、思考、交流中资源共享,寻找策略最优化,培养探究意识,提高探究能力。】
●探究活动二:包装三盒糖果。
师:想一想,哪种包装方案最节约?
(请三名学生上台展示不同的包装方案,教师同步出示课件)
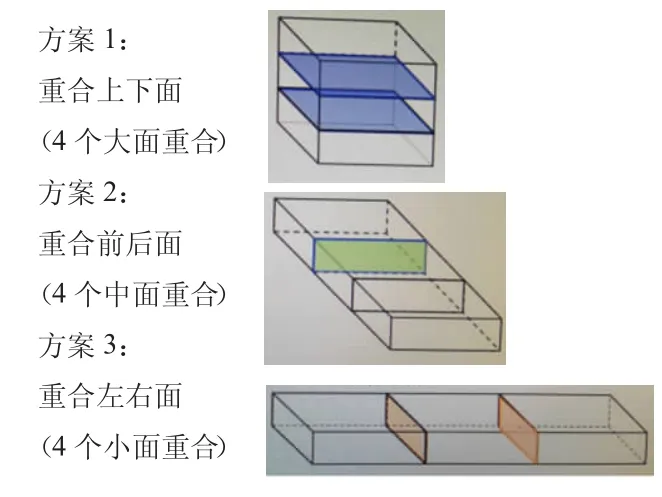
师:结合包装两盒糖果的最节约方案思考,能否不计算就知道哪一种方案最节约包装纸?为什么?
预设:第一种方案最节约包装纸。三种方案都是把三个长方体的表面积之和减去重合的面积。第一种方案减去的是4个大面的面积,第二种方案减去的是4个中面的面积,第三种方案减去的是4个小面的面积。重合的面积越大,剩下的表面积越小。
师:比较包装两盒糖果和三盒糖果,有什么发现?
预设:表面积之和不变,重合面越大,减去的面积越多,其包装面积越小。
【设计意图:在包装两盒糖果的基础上,探究三盒糖果的最优包装策略,通过想一想、摆一摆,再观察比较重合的面,使学生容易得出结论。】
师:是不是所有包装都只要把大面重合在一起就最节约包装纸呢?大家愿意接受更大的挑战吗?
●探究活动三:包装四盒巧克力。
师:一盒巧克力外包装盒的长为110mm、宽为70mm、高为36mm,包装四盒这样的巧克力最少需要多少包装纸?
1.摆一摆或画一画,用学具代替巧克力盒。(小组合作,比赛看哪一组完成时间最短)
出示小组合作要求:
(1)四人小组分工,摆一摆或画一画。
(2)要尽量多的考虑包装方案。
(3)思考最节约的包装方案并说一说理由。
2.说一说。
分两组展示,一组草图展示,一组学具展示,对每种方案作简单介绍,当包装方案有遗漏时,其他小组可补充展示介绍。
3.理一理,想一想。
师生共同按相同的面重合和不同的面重合来进行有序整理,出示课件。
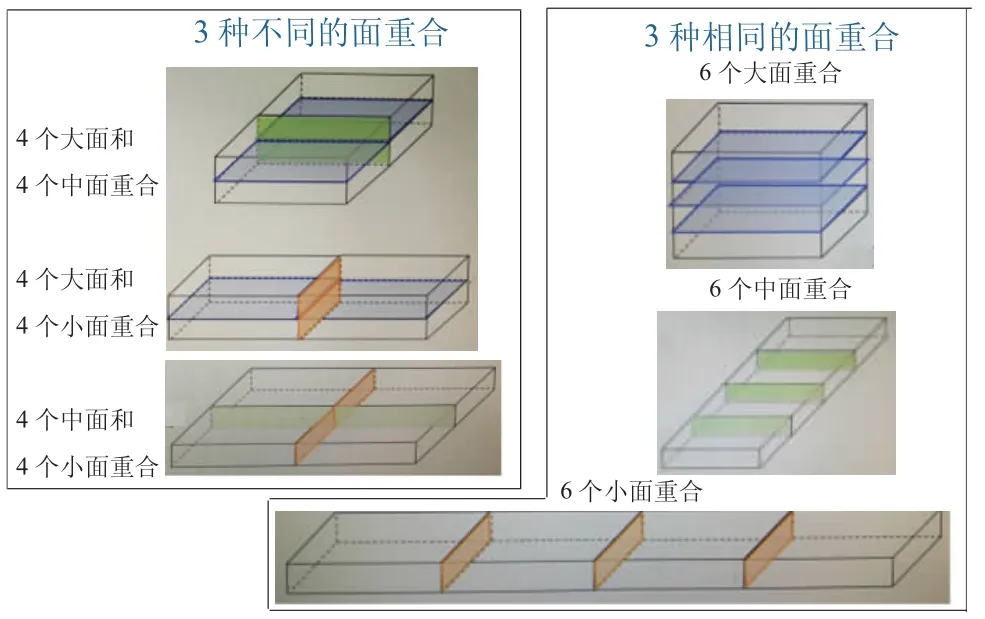
【设计意图:在探究四个相同长方体组合成新的长方体时,虽然大多数学生通过动手操作能得到六种拼摆方法,但可能会思维无序,探究活动有难度,因此小组分工合作非常有必要。在教师展示拼摆方案时要有意识地引导学生进行有序拼摆,不重复不遗漏又节约时间,对于包装方案的多样化和策略的最优化的归纳与总结很有帮助。】
探究思考:不计算,这六种方案中哪种最节约?说说理由。
预设1:6个大面重合的包装方案最节约。
预设2:4个大面和4个中面重合的包装方案最节约。
6个大面重合
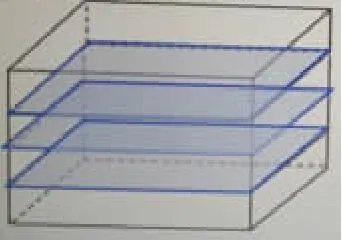
4个大面和4个中面重合
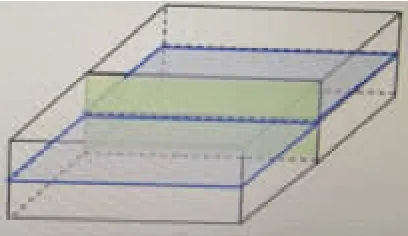
4.探究最节约的方案。
师:大家意见不一致,怎么办?(用数据验证,得出最节约的方案)
独立计算,探究,比较得出最简便的计算方法:
方案 A:110×70=7700(mm2)
方案 B:110×36×2=7920(mm2)
师:由于表面积之和不变,比较两种包装方案的表面积其实就是比较重合的6个大面和4个大面加4个中面的面积大小,也就是比较1个大面和2个中面的面积大小,谁大就是谁节约。四盒巧克力的包装方案中并不是大面重合面积最大,而是4个大面和4个中面重合后面积最大,所以与前面两种包装情况的最节约方案不同。
【设计意图:在包装方案的有序展示后,引导学生观察、比较、计算、交流为什么方案B是最优化策略,让学生通过实践、探究经历“再发现”的过程,帮助学生由直观向抽象迈进,提升数学核心素养。】
5.算一算。
根据最节约方案求出四盒巧克力所需包装纸的面积:
(110×70+110×36+70×36)×2×4-(110×36×4+110×70×4)=66800(mm2)
6.交流体会,归纳小结。
师:经历了两个、三个和四个相同长方体的包装,我们得出结论——重合的面积越大,表面积就越小,就越节约包装纸,这就是包装的学问。用表面积之和减去重合的面积就是包装纸的表面积。
(板书:重合的面积越大,表面积就越小,
表面积之和-重合的面积=包装纸的表面积)
【设计意图:四个长方体的包装是本课的一个难点,教学分三个部分进行:首先探究有多少种包装方案。然后引导学生分析、猜测哪种方案最节约包装纸。因为学生的观察角度不同,在最优策略上可能会有争执,因此开展第三层次的探究,通过计算验证猜测,进一步归纳最节约包装纸的原因,培养学生的探究意识,加深学生的理解。】
三、回顾总结,畅谈收获
师:刚才在研究糖果和巧克力的包装过程中,同学们发现了一些有趣的现象和规律,谁来说说今天的收获?
预设:
1.有多种包装方案。
2.会计算组合长方体的表面积。
3.知道怎样包才能节约包装纸。重合面积越大,表面积越小。
【设计意图:通过回顾梳理,总结反思,让学生对包装的学问有了总体的认识,培养探究意识,提升核心素养。】
四、回归生活,巩固应用
师:(课件再次出示上课前的一些商品包装图片)观察这些包装形式,你认为合理吗?为什么?
总结:同学们,包装虽小,可里面的学问却不少,今天我们只是从数学的角度研究了如何节约包装纸,实际生活中包装还要考虑美观、好保管和便于携带等因素。希望同学们今后在生活中用心观察,细心思考,做个有心人。
【设计意图:让学生进一步体会到数学来源于生活又应用于生活。】
