载人潜水器耐压壳体结构疲劳可靠性分析

李金华，白德乾，刘铁生,3

(1. 齐鲁工业大学(山东省科学院)，山东省科学院海洋仪器仪表研究所，山东省海洋监测仪器装备技术重点实验室，国家海洋监测设备工程技术研究中心，山东 青岛 266061；2. 哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨 150001；3. 青岛中乌特种船舶研究设计院有限公司，山东 青岛 266061)

载人潜水器是进行海洋探索、科学考察和海底施工作业的装备，是和平开发利用海洋资源的重要技术手段，也是海洋开发技术的制高点之一，能够充分展现一个国家的综合技术实力[1]。耐压球壳是保障载人潜水器正常工作和潜水员生命安全的关键结构，载人潜水器每完成一次下潜任务都将承受大幅交变载荷作用，因此，耐压球壳在服役期间会承受周期性的往复应力，由此引起的低周疲劳损伤成为影响其结构安全性的重要因素。目前，国内外潜深超过3000 m的载人潜水器载人舱球壳材料几乎全部采用钛合金材料[2]。陈承皓[3]发现，钛合金结构的失效事故中约有70%是因为疲劳断裂造成的。由于载人深潜器工作环境的特殊性，研究人员无法通过大量的现场实验得到耐压壳体疲劳可靠性数据，国内外许多学者应用多种模型和方法对其进行了分析。王莹莹[4]基于断裂力学的疲劳寿命预报统一方法，将保载效应的裂纹扩展率修正模型和可靠性分析方法相结合，对潜水器载人舱的疲劳可靠性进行了分析；陈承皓等[5]基于全寿命裂纹扩展模型对钛合金球壳进行了可靠性分析；朱永梅等[6]应用FEMFAT软件对完整球壳和开口球壳进行了疲劳寿命的对比分析，结果表明开口球壳的使用寿命与完整球形耐压壳相比下降了32.4%；薛鸿祥等[7]基于响应面法对4500 m级载人深潜器耐压球壳开展了疲劳可靠性分析，得到了失效概率及各随机变量参数敏感性结果；李良碧等[8]应用有限元方法对大深度载人潜水器疲劳寿命进行了计算。由于缺少大量的实验验证，目前应用各种模型计算得到的耐压球壳可靠性的结果并不统一。本文以4500 m级大深度载人潜水器的耐压壳体为研究对象，基于结构可靠性理论和有限元分析方法对其进行疲劳分析；考虑球壳开口处的应力集中的影响，基于应力-干涉模型对壳体的疲劳可靠性进行计算，为载人潜水器耐压壳体的结构设计和疲劳寿命估算提供参考依据。

1 耐压壳体强度计算

1.1 耐压壳体疲劳载荷分析

1.1.1 疲劳载荷

对于载人深潜器，作用在耐压壳上的主要外部载荷是海水静压力，本文采用GL规范[9]推荐公式对海水静压力进行计算：

p=0.010 1×d，

(1)

式中，p为球壳所受外部静水压力，MPa；d为下潜深度，m。

1.1.2 疲劳载荷谱

本文研究对象为4500 m级钛合金球壳载人潜水器，与美国的Alvin号属于同级别。 Alvin号工作环境与我国潜水器相似，且是唯一有详细的下潜数据的现役大深度潜水器。因此，从Alvin号所属单位Woods Hole 海洋研究所网站上获得了详细下潜数据[10]，并对其进行处理得到下潜载荷谱，如图1所示。

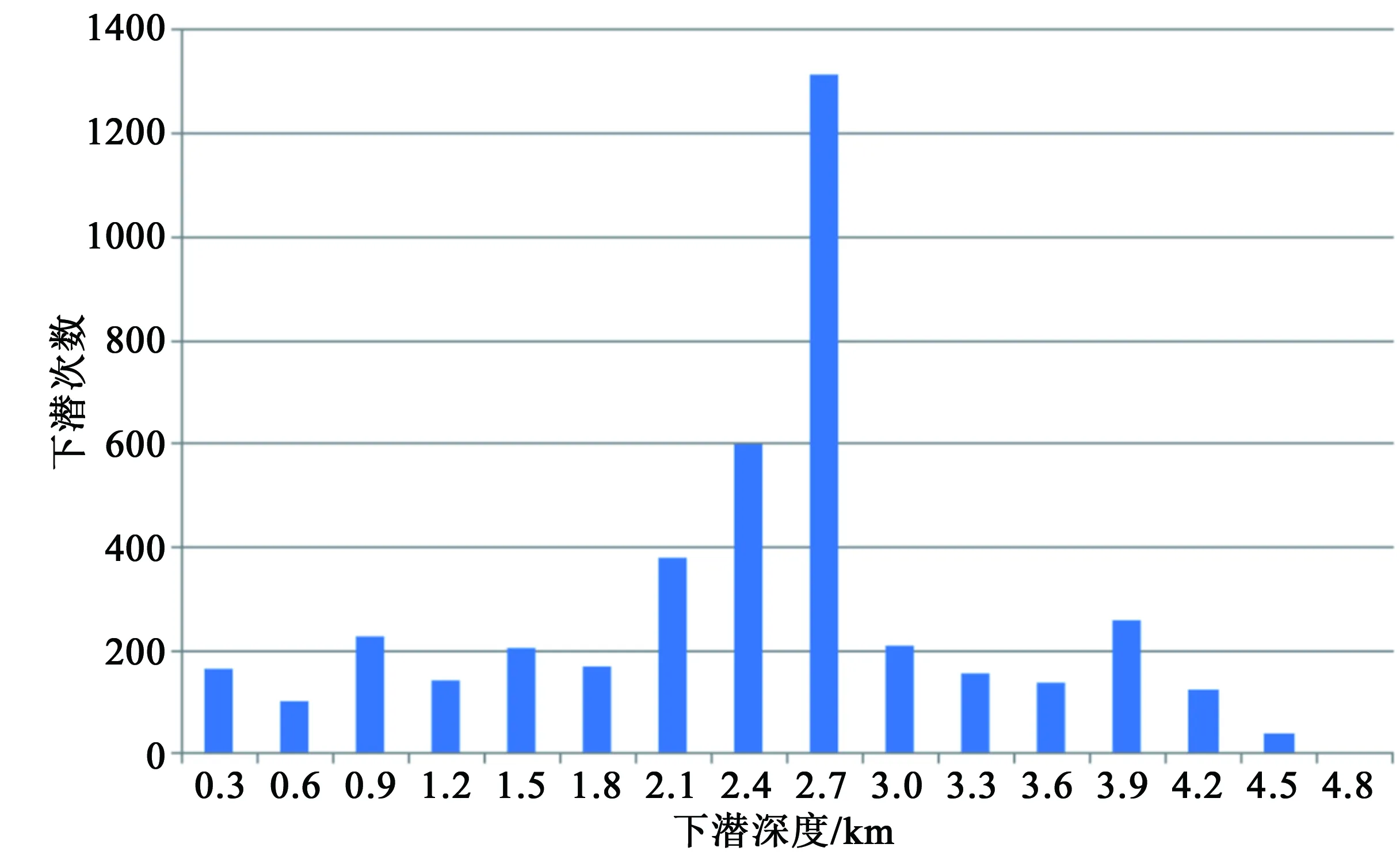
图1 Alvin号下潜载荷谱Fig.1 Alvin′s diving load spectrum

由图1可以看出，Alvin号在2700 m附近下潜次数最多，此时耐压壳所受海水静压力大约是27 MPa，且载荷与下潜深度呈线性关系。对Alvin号下潜数据使用Gumbel分布函数进行拟合，得到下潜深度d的概率密度函数：

(2)

对下潜深度进行等效正态化，获得均值为2 384.13 m，标准差为742.93 m的正态分布。根据国外在役深潜器下潜情况[1]，假定载人深潜器设计寿命是20年，每年下潜作业200次左右，载人耐压壳的疲劳设计循环可设定为4000次。从上述分析可以看出，载人潜水器耐压壳的疲劳问题属于典型的低周疲劳问题。

1.2 耐压壳体参数

本文研究的球形耐压壳体的基本参数为：主尺度内径2.1 m，厚度80 mm；人员出入孔1个，直径500 mm。耐压壳体材料选用Ti80钛合金，本文计算时，Ti80钛合金的屈服强度取785 MPa，弹性模量为1.15×105MPa，泊松比为0.3。

1.3 耐压壳体强度理论数值计算

假设球壳中面的曲率半径为r，厚度为t，根据经典板壳理论，一般把球壳按照厚度-半径比t/r的大小分为薄壳和厚壳两种。薄壳的厚度半径比小于0.05，可按照薄壳理论进行计算；反之则为厚球壳。本文耐压球壳厚度半径比λ：

(3)

属于中厚壳范围，下面分别用薄壳理论和厚壳理论进行计算并对比。

1.3.1 薄壳理论

根据薄壳理论，以壳体中面上的应力来代替球壳因受力变形而产生的应力。壳体中面上的内力可以分为薄膜应力和弯曲应力。根据无矩理论，即在分析球壳应力水平时只计及球壳的薄膜应力而不把弯曲应力计算在内，可得：

(4)

式中，σ为球壳周向薄膜应力，MPa；p为静水压力，MPa；将球壳主尺度数据代入上式，得：

σ=6.812 5p。

(5)

1.3.2 厚壳理论

本文使用受均匀静压力的封闭厚球壳的精确强度理论解[11]来计算载人潜水器耐压壳体的应力水平。径向应力与周向膜应力相比可以忽略不计，故只计及周向膜应力。周向膜应力的表达式如下：

(6)

(7)

将球壳主尺度数据代入得：

σmax=6.550 2p。

(8)

从计算结果来看，在耐压球壳承受相同的外部静水压力时，应用薄壳理论和厚壳理论两种方法所得结果比较接近，厚壳理论计算结果较小。

本文研究的球形耐压壳结构由于设有一个直径500 mm的人员出入口，在出入口位置附近存在应力集中现象，是疲劳计算的关键部位，因此需计算球壳开口处的应力集中系数。应用文献[12]中提供的方法，可计算得到球壳开口处的应力集中系数为1.406。因此计算疲劳可靠性时，球壳的应力应为：

σ=1.406×6.812 5p。

(9)

1.4 耐压壳体有限元分析

1.4.1 耐压球壳有限元模型

ANSYS软件疲劳分析模块是后处理程序的一个模块，以ASME锅炉和压力容器规范(ASME Boiler and Pressure Vessel Code)[13]第三节和第八节第二部分作为计算的依据，采用简化了的弹塑性假设和Mimer累积疲劳准则，因此用于潜水器耐压壳体的疲劳分析是完全合适的。计算中涉及到一些疲劳参数，如：热点位置、应力幅、载荷等。

耐压球壳内径2.1 m，有1个人员出入孔，直径500 mm。耐压球壳厚度半径比0.073 39，属于中厚壳范围。在ANSYS有限元分析软件中建模时采用8节点solid185单元，在厚度方向分成若干层，整个球壳共分成6276个节点，4608个单元，图2 为耐压球壳有限元模型。

图2 耐压球壳有限元模型Fig.2 Finite element model of pressure spherical shell

1.4.2 边界约束

大深度潜器在海底作业时，仅受浮力和重力作用，当对耐压壳体进行分析时，需施加足够多的约束条件，壳体需要3点支持，约束6个位移分量，边界条件对称设置，这样既可以消除整个刚体位移又不妨碍相对变形。如图3所示，在壳体位于x轴和z轴的位置上，相隔90 °取3个点：位于x轴上的节点A和C，令μz=μy=0，位于z轴上的节点B，令μx=μy=0，节点A和C对称于原点。 其中，μx为沿x轴方向的位移，μy为沿y轴方向的位移，μz为沿z轴方向的位移。

图3 边界约束条件Fig.3 Boundary constraints

1.4.3 有限元分析结果

本文研究的4500 m级载人潜水器，耐压球壳所受外部静水压力约为45 MPa，载荷与下潜深度呈线性关系，所以分别取下潜深度为1000 m、2000 m、3000 m、4000 m、5000 m、6000 m时的静水压力(表1)，对耐压球壳外表面进行加载求解，最后对计算结果进行线性拟合，得到耐压球壳应力与静水压力p的函数关系式。

表1 不同外载荷下耐压球壳最大应力

应用MATLAB对表1数据用一次线性拟合并绘制拟合图，见图4。

σmax=9.877 1p+0.466 7。

(10)

图5所示为耐压球壳应力云图，结果显示，在不同外载荷下，耐压球壳应力最大值都出现在人员出入孔附近。对疲劳寿命起关键性影响的部位是应力集中部位，在疲劳可靠性分析中应重点分析，所以提取最大应力点，并记下节点号4981。

1.5 耐压壳体强度校验

从上述分析可知，开口壳体理论上更易发生应力集中，而开口壳体的有限元计算结果大于应用式(9)理论计算的结果，从安全角度出发，选用有限元计算结果进行耐压壳体强度校验。依据文献[14]，耐压球壳应力应满足下式：

σmax≤0.85ReH，

(11)

式中，ReH为材料的屈服强度，σmax是潜水器下潜至4500 m时耐压球壳的应力。本文耐压球壳选用的Ti80钛合金的屈服强度785 MPa：

0.85ReH=0.85×785=667.25 MPa 。

(12)

结合式(1)：

σmax=9.877 1p+0.466 7=9.877 1×0.010 1×d+0.466 7=499.260 25<0.85ReH。

(13)

上述计算结果显示，该耐压壳体在下潜至设计深度时的最大应力满足《潜水系统和潜水器入级与建造规范》[14]对于强度的要求。

2 耐压壳体可靠性计算

通过应用ANSYS的疲劳计算模块，选取4981号节点应力作为第一载荷应力对耐压球壳进行疲劳分析，得到了疲劳分析结果。结果显示耐压球壳的疲劳寿命为1×107次，说明设计寿命4000次是安全的。

下面基于应力-强度干涉模型对耐压壳体结构进行疲劳可靠性分析。应力-强度干涉模型根据结构的疲劳载荷得到结构的疲劳应力，把结构的疲劳极限σD作为疲劳强度。由图1得到的疲劳载荷谱可得到耐压壳的疲劳应力，根据文献[15]提出的多参数经验公式(14)计算耐压壳体材料的疲劳极限σD：

σD=f(E,ReH,Kt,S) 。

(14)

也可以写成

σD=aReH+bE+c，

(15)

其中，Kt是应力集中系数，S是循环载荷的应力比，E是材料的弹性模量。a、b、c是3个系数，分别是：

a=0.139e-0.302KtS2+0.435e-0.395KtS+0.836e-0.480Kt，

b=(0.473e-0.577KtS2+1.479e-0.670KtS+2.842e-0.755Kt)×10-3，

c=12.0KtS+28.2Kt-82.8S-191。

2.1 应力σ与强度s及二者差的概率密度函数

当应力σ与强度s都是正态分布时，其概率密度函数为：

(16)

(17)

(18)

2.2 可靠度表达式

可靠度l由Z为正值时的概率表示：

(19)

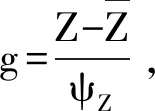
(20)

上式也可以记作：

(21)

上面两个式子中Y为：

(22)

上式是应力强度和可靠度的联结方程，Y称为联结系数，也叫安全指数或可靠性指标，此时用β表示。

2.3 耐压壳可靠度

3 结论

本文通过应用应力-强度干涉模型，对4500 m级载人潜水器进行疲劳可靠性分析，应用ANSYS对载人潜水器耐压壳体结构进行疲劳分析。计算结果显示，耐压壳体在使用周期4000次内是安全的；在不考虑应力集中影响的情况下，计算得到可靠度指标为4.555 2，而考虑应力集中影响，其疲劳可靠度指标降为2.034 5。因此，在设计载人潜水器耐压壳体结构时，应采取必要的加强措施减小出入口、观察舷窗等开口位置的应力集中，从而延长潜水器的使用寿命。