焊接残余应力对深潜器耐压球壳承载能力的影响

徐 磊，黄小平，王 芳

（1.上海交通大学 海洋工程国家重点实验室 高新船舶与深海开发装备协同创新中心，上海200240；2.上海海洋大学 上海深渊科学工程技术研究中心，海洋科学学院，上海 201306）

焊接残余应力对深潜器耐压球壳承载能力的影响

徐 磊1，黄小平1，王 芳2

（1.上海交通大学 海洋工程国家重点实验室 高新船舶与深海开发装备协同创新中心，上海200240；2.上海海洋大学 上海深渊科学工程技术研究中心，海洋科学学院，上海 201306）

耐压球壳通常采用焊接方式将两个半球壳连接成整球，在焊缝处产生的接近材料屈服强度的焊接残余应力对球壳的承载能力有多大的影响，是否需要做焊后消除残余应力处理，将直接影响球壳的安全性和生产成本。而现有对球壳极限强度计算，无论是理论计算还是数值计算，均只考虑了球壳初始缺陷中的几何缺陷对球壳极限强度的影响。该文将在现有的耐压壳极限强度设计公式基础上，采用数值计算的方法对耐压球壳的焊接过程进行数值模拟，得到焊后球壳的焊接残余应力分布，并在此基础上考虑残余应力对球壳极限强度的影响，结果表明，对于大潜深厚球壳，焊接残余应力对耐压球壳承载能力影响不显著，为大深度潜器耐压球罐是否需做焊后消除残余应力处理提供了一定的参考依据。

耐压球壳；焊接；残余应力；极限强度

0 引 言

2012年6月，中国的大深度载人潜水器“蛟龙号”成功进行了深度为“7 000m”的海试，标志着我国的海洋深水资源探测与开发进入世界一流行列。

球型耐压壳是大深度载人潜器的重要结构。在保证球壳极限强度的前提下，耐压球壳的质量越小，则深潜器所能携带的科研设备就会越多，则深潜器在水下的功能就会越大。因此,对耐压球壳的极限强度进行精确的预报就显得至关重要。对于球壳结构的极限强度，已有很多学者对此进行过研究，并进行了相应的实验。陆蓓等[1]运用非线性有限元计算了一系列半径厚度比（t/R）和不同初始扰度（Δ）下的耐压球壳的极限强度，并对几个主要球壳极限强度计算公式进行了比较。文献[2]在前人的基础上考虑了横向剪切变形对耐压球壳极限强度的影响。文献[3]讨论了耐压球壳上的开孔、特征值屈曲模态初扰度缺陷和局部初扰度缺陷对球壳的极限强度的影响，得出了特征值屈曲模态缺陷来处理初扰度是对结构最为不利的一种缺陷形式。文献[4-5]在总结前人的工作上，结合现有的球壳极限强度计算公式，进行了一系列的耐压球壳模型试验，并给出了一条用于计算耐压球壳极限强度的经验公式。

在以上的研究中，均只考虑了初始扰度缺陷对耐压球壳的极限强度影响。然而，在制造深潜器载人耐压球壳时，通常需要对制造好的两个半球耐压球冠进行焊接。当前深潜器耐压球壳的材料绝大多数采用的是钛合金，钛合金的焊接通常采用的是高能真空电子束焊。焊接完成后，耐压球壳的焊缝处将引入焊接残余应力。对于厚度较大的中厚度的耐压球壳，其失效主要是因为材料达到屈服后而引起的材料屈服失效，而不是因为球壳的失稳失效。因此，研究球壳焊接后焊缝处的残余应力对耐压球壳的极限强度的影响就显得极为重要。

1 球壳极限强度理论

1.1 球壳线弹性失稳理论

当球壳的壳厚比t/D≤1/20时，球壳可以按照薄壳来处理。薄壁球壳在外压下失稳的理论解由Zoelly[6]于1915年提出，见（1）式。其中：Pe为失稳压力，E为材料的杨氏模量，R为球壳的半径，t为球壳厚度，μ为泊松比。

通常，大深度载人潜水器的耐压球壳的壳厚比t/R≥1/12，不属于薄壳范围。考虑到材料的非线性与几何形状的非完善性，并且加上焊接时引入的残余应力，经典的弹性球壳失稳极限强度理论与实际的耐压球壳极限承载能力有很大差别，经典理论并不适用于计算深潜器耐压球壳的极限强度。

1.2 球壳材料屈服强度理论

随着t/R的增加，耐压球壳的极限强度不能由失稳来决定，而是当球壳受压时，球壳的应力水平达到材料的屈服，所导致的材料屈服来决定。由结构力学的知识，球壳在外压P的作用下，考虑材料的屈服强度σy，可以在材料非线性的情况下算得球壳的极限承载压力Py，其中Rm为球壳中径，t为壳厚。

1.3 俄罗斯深潜器球壳设计公式

对于深潜器的极限强度研究，俄罗斯学者Paliy和他的同事在克雷洛夫船舶科学研究院对其6 000 m的深海载人潜器研究中做出了一些理论研究和基础实验，并给出了计算钛合金耐压球壳的极限承载外压的经验公式[9]：

其中：rσ是线弹性失稳压力Pe与球壳材料屈服压力Py的比值，Pe由（1）式算得，Py由（2）式算得；r△为初始扰度缺陷对球壳极限承载压力的影响，其值为初始扰度△与球壳厚度t的比值 △/（ ）t。

2 耐压球壳焊接残余应力的数值模拟

2.1 耐压球壳的几何参数

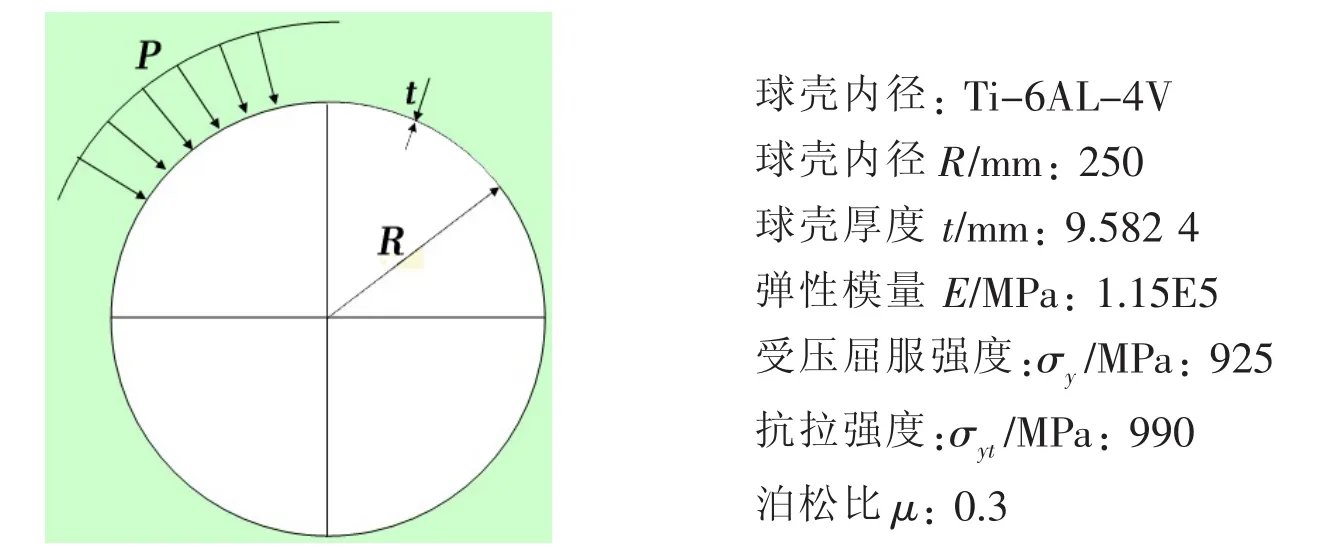
图1 耐压球壳模型图及其物理参数Fig.1 Spherical pressure hull model and parameters

2.2 热源函数的选取

对于大部分焊接而言，焊接热源是实现焊接过程的基本条件。由于焊接热源的局部集中热出入，致使焊接变得十分不均匀。焊接过程中，处于焊点的材料温度迅速达到焊料的熔点，而远离处的材料的温度几乎没有什么改变。因而钛合金耐压球壳在焊接过程中存在十分不均匀和不稳定的温度场，进而导致焊接后耐压球壳出现较大的焊接残余应力。

因此，能否选取合适的热源模型，对耐压球壳的焊接残余应力的计算至关重要。为了比较准确地模拟出钛合金高能电子束焊接的过程，将选取高斯分布面热源与高斯柱状体热源组成的组合热源作为高能电子束焊接的热源模型[7]。

高斯分布面热源：

其中：其中qm1为高斯分布面热源最大热流密度，qm2为高斯柱状体热源最大热流密度；Q为电子束焊接功率，H为电子束焊接穿透厚度，即为球壳厚度t，η=0.2为功率分配系数，r0=2mm为电子束加热光斑半径，r为焊件上各点到电子束光斑中心的距离，z为沿厚度方向距加热表面的距离，m为高斯柱状热源的溶池形状系数，本文根据典型高温合金溶池实际情况，结合参考文献[7]，取m=-0.017 5。

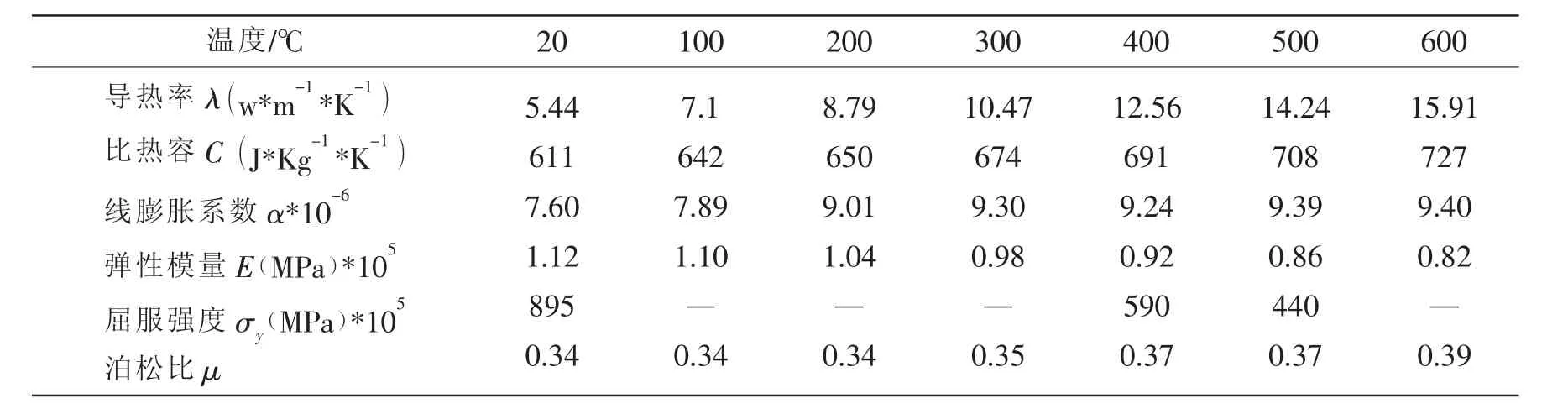
表1 Ti-6AL-4V热物理性能参数[8]Tab.1 The materialproperty coefficients of Ti-6AL-4V[8]

2.3 有限元模型建立

进行耐压球壳的焊接数值模拟时，对焊缝位置需要尽可能的细化，为此将产生数量巨大的网格。若建立整个完整的球壳模型，将以花费巨大的计算时间为代价。考虑到球壳的轴对称结构，进行多次尝试，对计算精度和计算时间进行权衡后，选取1/8球壳的球壳模型来进行有限元计算，整球壳的极限强度是否能用1/8球壳来代替，在表3中进行了讨论。

2.3.1 网格大小

本文中采用商业有限元软件ANSYS作为有限元计算软件，耐压球壳焊接温度场的数值模拟，模型建立采用热体单元solid70。经过多次的计算比较，焊缝处的网格为球壳沿厚度方向分15层，沿球壳周向方向划分360段。焊缝处体单元的大小为0.7×0.85× 1.4（单位mm），能够精确地模拟焊接过程的耐压球壳的温度场。

2.3.2 边界条件

边界条件的施加为：每个对称面施加对称边界条件。对流换热面为内表面与外表面，均施加对流换热系数。有限元模型如图2所示。

2.4 耐压球壳焊接温度场计算与结果

焊接过程的温度场分析：图3（a）为t=5 s时球壳焊缝表面的温度场分布示意图，图3（b）为t=5 s时球壳垂直焊缝方向上的温度场分布。可以看到，焊接过程中，焊接区域的温度场梯度很大，在电子束光斑加热区域，温度迅速达到2 700℃左右，远离热源的区域，温度保持室温不变。随着电子束加热光斑的移动，焊缝表面的温度场呈现狭长的卵形分布特征，热源前方的等温线分布密集，温度梯度巨大，加热光斑后方的等温线拉长成为椭圆形，且热源后方的等温线梯度较热源前方区域等温线梯度低。

图4为垂直于焊缝方向依次选取距离焊缝等间距节点的焊接热循环曲线。可以看到，随着节点距焊缝距离的增加（由0.0mm增加至6.8mm），相对应的节点最高温度依次递减。由节点距离=0.0mm时温度峰值2 700℃左右，到节点距离=6.8mm时峰值温度降为625℃左右。当焊接热源经过所选节点后，温度迅速降为280℃左右，然后进入一个缓慢的室温冷却过程。

图2 耐压球壳的有限元模型网格Fig.2 The FEM modelof sphericalpressure hull

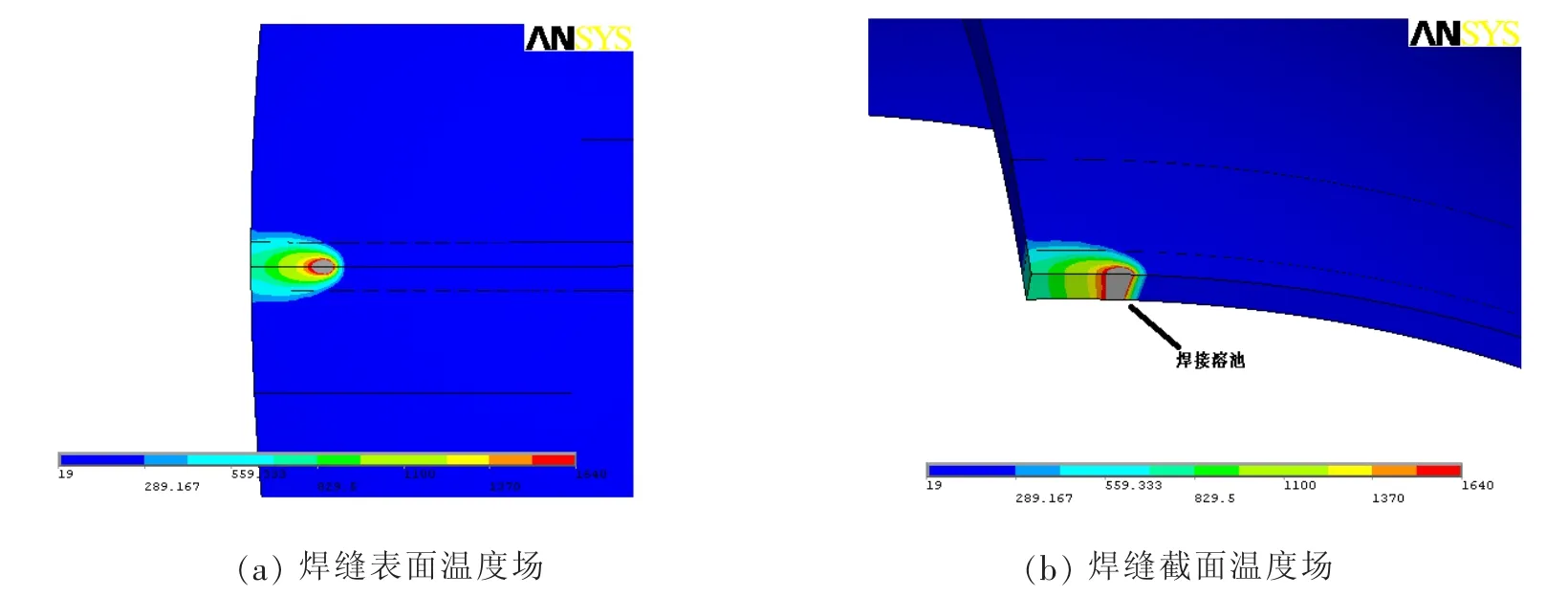
图3 t=5 s时的焊接温度场与焊接溶池形貌Fig.3 Temperature distribution and welding poolattime=5 s

2.5 球壳焊接残余应力分布

2.5.1 应力场求解过程

进行球壳温度场的数值计算后，以温度场为基础进行焊接残余应力场计算。有限元软件ANSYS中有两种耦合场的计算方法，一种是直接耦合法，另一种是间接耦合法。本文中的耦合场为热—结构耦合场。通过多次的实践，权衡求解时间和收敛性及精度后，本文将采用间接耦合场法计算耐压球壳焊接后的残余应力场。求解过程流程图如图5所示。

2.5.2 耐压球壳焊接应力结果

本次计算采用是在焊接电压U=1.4e6 kV，电流I=0.013 3A，焊接速度V≈5 mm/ s的高能电子束焊接工艺下进行的数值模拟，计算得到焊后焊接残余应力沿不同方向的分布结果如图6，图7所示。

由图6（a）得到，纵向应力沿焊缝方向整体表现为较高的拉应力，最大的拉应力在内表面，约为820MPa，由于边界条件的影响，焊接开始端与结束端的应力状态表现得比较复杂。由图7得到，纵向应力垂直于焊缝方向，有一个由正到负再趋向于零的过程：纵向残余应力在焊缝处表现为很大的拉应力，这是由于融化后的金属的冷却收缩造成的。随着距焊缝距离的增大，拉应力逐渐减小且逐步的转变为压应力，直至增大至约200MPa的压应力后，在远离焊缝的区域，又逐渐趋向于0 MPa。

图4 垂直焊缝方向典型节点的温度循环曲线Fig.4 Temperature history at vertical welding direction

图5 ANSYS热—结构耦合场分析流程图Fig.5 ANSYS thermal-structural analysis process

由图6（b）得到，横向应力沿焊缝方向表现得较为复杂，材料由于自身受力平衡的需要，并且球壳在焊接完成后，焊缝处会出现较为明显的“颈缩”现象，拉应力和压应力在焊缝处同时存在。球壳内表面表现为拉应力，最大约为320MPa左右；球壳外表面表现为压应力，约为200MPa左右。在垂直于焊缝方向上，横向残余应力也随着距离焊缝距离的增大，上下表面的拉或压横向残余应力也逐渐趋向于零。

除通常讨论的横向与纵向残余应力以外，球壳厚度方向也还存在这明显的轴向应力。球壳的轴向应力整体表现为拉应力，最大的轴向应力存在于外表面处，约为70 MPa。

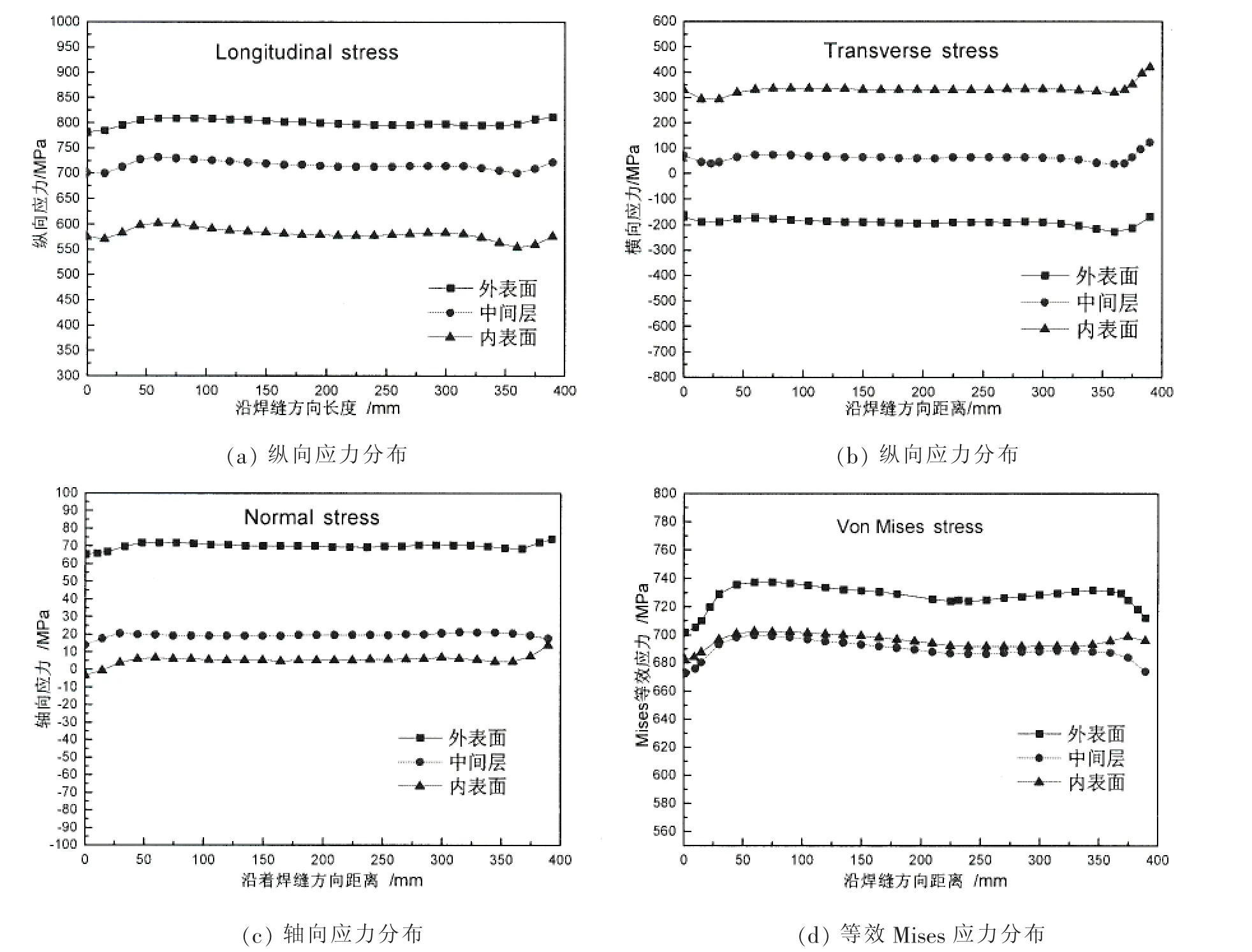
图6 沿焊缝方向球壳内外表面的焊接残余应力Fig.6 Welding residual stress distribution at welding direction

图7 垂直焊缝方向球壳内外表面的焊接残余应力Fig.7 Welding residual stress distribution at vertical welding direction

3 焊接残余应力对耐压球壳极限强度的影响及验证

3.1 残余应力的施加与初始位移缺陷的处理

耐压球壳的焊接残余应力场计算完成以后，将冷却后的残余应力作为应力结果文件保存。建立新的进行极限强度分析的耐压球壳结构模型，对耐压球壳的线弹性模态屈曲分析，求出其1阶模态，对球壳施加与1阶失稳波形一致的初始缺陷并保存，然后将焊接残余应力作为初始应力读入模型中，运用弧长法对球壳进行非线性运算，求得极限压力。图8所示为球壳一阶屈曲模态示意图；图9，10所示为焊接残余应力等效云图和球壳极限压力求解过程。

图8 球壳一阶屈曲模态Fig.8 Spherical pressure hull first mode

图9 焊接残余应力等效云图Fig.9 Mises Stress of welding residual stress

3.2 结果讨论与实验结果验证

本文为验证焊接残余应力对球壳极限强度的影响，选取文献[5]中的2#耐压球罐，分别计算了：① 无焊接残余应力的整球壳极限强度；② 无焊接残余应力1/8球壳极限强度；③ 考虑焊接残余应力1/8球壳极限强度；④公式（1）、（2）、（3）的球壳极限强度理论值；并与实验结果值进行对比。

由表3可知，不考虑焊接残余应力时，整球壳的极限强度Pu值与1/8球壳的极限强度Pu值相差的绝对值最大值为2.17MPa（△=3 mm时），相差百分比最大仅为4%左右，则认为建立1/8耐压球壳模型，并施加相应的对称边界条件，能够准确模拟整个球壳的极限强度。同时也极大地减小了球壳焊接数值计算的代价。

公式（1），Zoelly公式考虑的是球壳的失稳压力，由表3中数据可以看到，球壳的失稳极限压力远大于实际的球壳破坏压力，因此，对于中等厚球壳或者厚球壳，公式（1）并不能准确地预报球壳的极限强度。

公式（2）是以材料屈服为准则，建立在力学知识上的计算公式，其计算结果与初始缺陷较小时的计算值比较接近，而其缺陷是，没有考虑到初始缺陷对球壳极限耐压强度的影响。实验结果表明，球壳的初始缺陷对球壳的极限耐压强度有着很密切的关系。

公式（3）的计算值与实际值的对比表明，公式（3）的计算结果偏于保守，对球壳的初始缺陷太过敏感，初始缺陷的稍微增加，球壳极限耐压值将迅速减小。这样将导致设计出的深潜器安全系数过大，不能最大限度地发挥材料的性能，并且加大了深潜器的自重，所能携带的设备必将减小。

图10 球壳极限压力求解过程Fig.10 FE analysis process of ultimate pressure

将表3中无残余应力1/8球壳Pu值与有残余应力1/8球壳Pu值进行对比，无残余应力的Pu值比有残余应力的Pu值大，二者最大差值为4.25MPa（Δ=4 mm时），相差的最大百分比为8.92%。可以发现，考虑焊接残余应力后，耐压球壳的极限强度有一定的减小，但减小的幅度并不是很大，在原有引入初始缺陷的基础上，减小幅度为0.53～4.25MPa之间。

表3 球壳极限强度不同计算结果对比Tab.3 Ultimate Strength comparison between different results

4 结 论

本文基于现有的耐压球壳极限强度计算公式，结合有限元数值计算，给出了耐压球壳焊接后焊缝处的残余应力分布，并在此基础上讨论了焊接残余应力对耐压球壳的极限强度影响，得出了以下结论：

（1）在不考虑焊接残余应力的前提下，用1/8球壳模型，并施加相应的对称边界条件，1/8耐压球壳的有限元模型能够准确计算中厚完整球壳的耐压极限值，误差在5%以内。

（2）球壳的极限强度受初始位移缺陷的影响十分明显，随着初始位移缺陷的增加，球壳的极限强度明显减小。不考虑缺陷影响的计算公式误差比较大。已有的考虑初始扰度缺陷的俄罗斯潜水器耐压壳计算公式（3）的计算值过于保守，需要进一步更新现有的计算耐压球壳极限强度的经验公式。

（3）球壳焊接完成后引入的焊接残余应力对耐压球壳的极限强度影响比较小，在考虑原有初始位移缺陷的基础上，略有减小。对于安全系数较大（例如1.5左右）的耐压壳设计，可以忽略残余应力的影响。对于安全系数较小（1.2左右）的耐压壳设计，精确预估焊接对耐压强度的影响十分必要，需要对焊接后的耐压球壳采取消除残余应力的必要措施。

[1]陆 蓓,刘 涛,崔维成.深海载人潜水器耐压球壳极限强度研究[J].船舶力学,2004,8(1)：51-58. Lu Bei,Liu Tao,Cui Weicheng.Ultimate strength of pressure spherical hull in deep-sea manned submersible[J].Journal of Ship Mechanics,2004,8(1)：51-58.

[2]李良碧,万正权.焊接残余变形对耐压环肋圆柱壳稳定性的影响[J].船舶力学,2016,20(1-2)：120-126.Li Liangbi,Wan Zhengquan.Effects of welding residual deflection to the stability of deep sea pressure ring-stiffened cylindrical shell[J].Journal of Ship Mechanics,2016,20(1-2)：120-126.

[3]俞铭华,王仁华,王自力,李良碧.深海载人潜水器有开孔耐压球壳极限强度研究[C]//2005年船舶结构力学学术会议论文集,中国浙江舟山,2005.

[4]Pan B B,Cui W C,Shen Y S,Liu T.Further study on the ultimate strength analysis of spherical pressure hulls[J].Marine Structures,2010,23(6)：1-18.

[5]Pan B B,Cui W C,Shen Y S.Experimentalverification ofthe new ultimate strength equation of spherical pressure hulls[J]. Marine Structures,2012,29(1)：169-176.

[6]Zoelly R.Über ein Knickungsproblem an der Kugelschale[D].Thesis,Zürich,1915.

[7]张彦华.焊接力学与结构完整性原理[M].北京：北京航空航天大学出版社,2007：80-88.

[8]中国航空材料手册编辑委员会编.航空材料手册[M].北京：中国标准出版社,2002：104-131.

[9]Paliy O M.Weight characteristics,reliability and operational safety of deep-sea submersible hulls[C]//In：International Symposium on Marine Structures(ISMS’91).Shanghai,China,1991：197-199.

Effect of welding residual stress on the ultimate strength of spherical pressure hull

XU Lei1,HUANG Xiao-ping1,WANG Fang2
(1.State Key Laboratory of Ocean Engineering,Collaborative Innovation Center for Advanced Ship and Deep Sea Exploration, Shanghai Jiao Tong University,Shanghai 200240,China;2.Shanghai Engineering Research Center of Hadal Science and Technology,College of Marine Science,Shanghai Ocean University,Shanghai 201306,China)

The present theoretical and numerical calculation on the ultimate strength of spherical pressure hulls only take the initial displacement imperfection into consideration.However,it will bring welding residual stress when constructing a spherical pressure hull,then it is necessary to evaluate the effect of welding residual stress on the ultimate strength of spherical pressure hull.In this paper,a series of current existing empirical design rules and equations was used to calculate the ultimate strength of pressure hull.Combined with the FEM method,the welding numerical simulation of the spherical pressure model was conducted and the welding residual stress distribution was given.Finally,the effect of welding residual stress on ultimate strength ofspherical pressure hull will be investigated and the results of this paper will offer some guide for the fabrication process of postweld heat treatment.

spherical pressure hull;welding;residual stress;ultimate strength

U661.43

A

10.3969/j.issn.1007-7294.2017.07.008

1007-7294（2017）07-0864-09

2017-01-21

国家自然科学基金重点项目：大深度载人潜水器载人球壳的结构可靠性研究（51439004）；国家自然科学基金面上项目：全海深马氏体镍钢载人球的设计和寿命计算方法研究（51679133）

徐 磊（1989-），男，硕士研究生；

黄小平（1963-），男，副教授，通信作者，E-mail：xphuang@sjtu.edu.cn。