三维编织碳/酚醛复合材料高温热响应的数值计算

2019-04-15李旭东

航空材料学报 2019年2期

张拜,李旭东

（兰州理工大学省部共建有色金属先进加工与再利用国家重点实验室，兰州 730050）

热防护系统（thermal protection system，TPS）是用来保护空间飞行器在高温环境中免遭烧毁或过热的结构和材料。碳/酚醛复合材料作为理想的热防护材料，具有耐高温、耐烧蚀、抗冲击等特点，被广泛地应用于航空航天领域[1-2]，如飞行器头部、固体火箭发动机喷管、返回舱防热罩等。随着航空航天技术的快速发展，飞行器部件服役环境更加苛刻，开发新型碳/酚醛热防护材料尤为重要。在这类热防护材料的研制过程中，准确预测高温条件下防热材料的热响应行为，尤其三维温度场的演变规律，可以为热防护系统的设计和优化、解决防热过度冗余或不足提供有效的参考和依据。

为了准确预测碳/酚醛复合材料的热响应行为，首先要考虑温升过程中防热材料内部发生的物理化学变化[3]。在加热过程中，酚醛基体与碳纤维最大的不同是前者发生了热分解反应而后者没有。酚醛树脂高温热解后，会在基体表面形成多孔炭层并释放出热解气体。一方面，多孔炭层随着温度的升高和加热时间的延长而变厚，并且充当隔热层进而保护内部结构，热解气体在炭层内的流动、换热等过程会对整个材料的温度场分布产生重要影响；另一方面，由于基体热解以及热解气体溢出材料表面，导致酚醛基体的密度发生衰减，产生质量损失。而与之相比较，碳纤维则始终保持恒定的材料密度，质量并未发生损失。在分析碳/酚醛复合材料热解炭化的基础上，很多学者已经对其高温条件下的热响应行为进行了大量的研究。Helber等[4]关注于表面炭层的消耗，将热解气体产物、外界环境、炭消耗率联系在一起，耦合求解了热力平衡条件下的表面能量和质量守恒方程。Paglia等[5]和Dec等[6]建立了简单的二维有限元模型，计算了加热条件下，碳/酚醛复合材料的温度场分布以及材料表面的形貌变化。与之相类似，易法军等[7]应用简化模型的方法，将三维材料结构转化为二维数值计算模型，预测了恒定热流边界下碳/酚醛复合材料的应力场和温度场分布规律。朱燕伟等[8]建立了碳/酚醛复合材料的整体模型，考虑了材料的炭化和热解气体的流动对能量方程的影响，计算了冷壁热流作用下防热材料的温度、气体压力、热解率等随时间和位置的变化过程。除此之外，文献[9～10]还针对高温环境中热解炭化型复合材料的物理化学变化过程建立了数学模型，这些模型基于材料内部的传热传质过程，求解了材料内部的瞬态温度场等变化情况。

分析现有的工作可以发现，目前对防热材料热响应的数值计算较多地采用了简化模型，这些模型将复杂的三维问题通过化简降维变为可求解的简单问题，从而极大地方便了数值计算。然而，应用简化模型预测的温度与实际情况出入较大[3,11-12]；并且，随着防热复合材料的发展，编织型复合材料在热防护系统中的应用越来越广泛，而一维或二维模型拟实性差,已经不能完全反映三维编织复合材料的真实情况；此外，文献中对三维编织碳/酚醛复合材料高温热响应的计算报道较少。基于此，本工作对基体和纤维束分开建模，利用能量和质量守恒方程，考虑热解过程中酚醛基体密度和材料热属性的变化，对三维编织碳/酚醛复合材料的高温热响应行为进行数值计算，预测复合材料瞬态温度场以及热解度的分布规律，研究质量损失率和炭层厚度的变化情况。

1 内部热响应计算

高温条件下，碳/酚醛防热复合材料的基体和纤维具有不同的行为特征。酚醛基体随着温度的升高发生热分解反应，材料被炭化，并且密度和热属性也随着热解过程的进行而不断地变化；而碳纤维则相对稳定，其密度和材料热属性均可视为恒定的常数。

1.1 热传导

在未发生热解反应时，材料内部的温度场由热传导方程计算：

1.2 基体热解

在加热过程中，酚醛基体的热响应涉及温度场、物性场、化学反应，是一个高度耦合的非线性过程。热解反应可表示为[13]：酚醛树脂→炭残余物（炭层） + 热解气体。

本工作在计算酚醛基体的热响应行为时，作了如下的简化和假设[14-15]：

（1）将酚醛基体处理为各向同性材料，因而各方向的材料热属性相同。

（2）热解气体与固体残余物间不发生化学反应，且两者保持热平衡。

基于以上假设，加热条件下酚醛基体的能量和质量守恒方程分别为[14-16]：

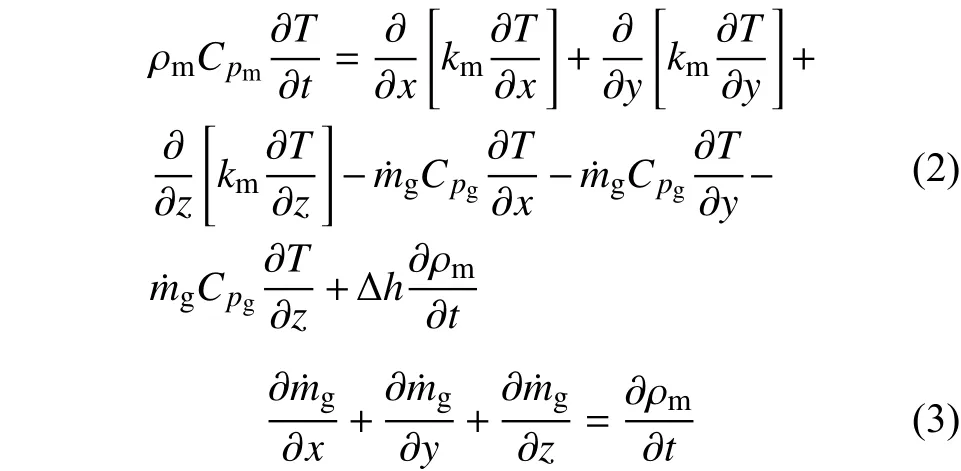
酚醛基体的热解反应速率应用Arrhenius动力学反应方程计算[15-16]：

2 基体热属性和加热面热流

在加热过程中，酚醛基体的传热是一个变物性的传热过程。开始时热属性为酚醛树脂的材料属性，而在加热到一定程度后基体完全被炭化，材料热属性变为多孔炭层的属性。在计算过程中，为了获得中间状态的材料性能参数，假设此状态的材料属性与加热过程中原始酚醛材料和完全炭化材料的相对质量分数有关，这一质量分数定义为[14-16]：

则中间状态基体的导热系数、比热容分别为[14-16]：

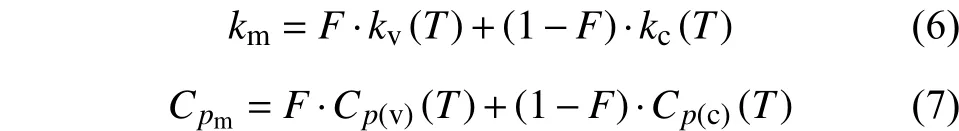
在恒定热流加热并考虑热解气体溢出表面带走热量的情况下，加热面的热流关系用下式计算：

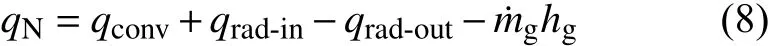
3 多尺度模型和纤维束材料属性

3.1 多尺度模型

在对碳/酚醛复合材料热响应行为的计算过程中，建立两种不同尺度的模型，如图1所示。对于宏观尺度模型，增强体为纤维束，其直径为0.27 mm，模型的长度和宽度均为12.5 mm，厚度为10 mm；纤维束由碳纤维编织而成，碳纤维直径d为7 μm；假设碳纤维在纤维束中呈直线均匀分布并且相互平行[17]，则细观尺度模型作为代表性体积单元（representative volume element，RVE）包含碳纤维和酚醛基体，其可由单根纤维、4根1/4纤维部分以及基体组成，该模型的长度 a为 8.2 μm，宽度 b为 13.9 μm，高度h为12.5 mm；细观尺度模型用来计算加热过程中细观RVE的材料属性值，该属性作为纤维束的材料属性应用于热传导方程，并结合基体热解方程最终实现对宏观材料结构热响应行为的计算。

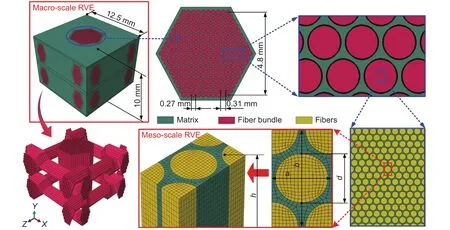
图1 碳/酚醛复合材料的几何模型Fig.1 Geometry model of carbon/phenolic composite

3.2 纤维束材料属性

加热过程中由于酚醛树脂的不断热解，基体的导热系数、比热、密度在材料内呈不均匀分布且其值随温度的变化而变化。因此，在应用细观尺度模型计算纤维束的材料属性参数时，对基体的材料属性取其平均值，而碳纤维由于未发生热解反应，其材料属性处理为常数。纤维束整体的属性参数由基体和碳纤维的属性参数加权得到，其导热系数或密度的计算式为[18]：

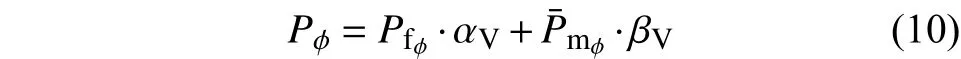
纤维束的比热计算式为[17]：

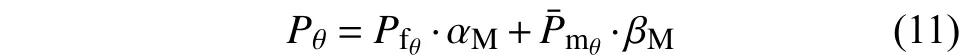
在细观尺度模型中，碳纤维所占的体积分数可用下式计算：

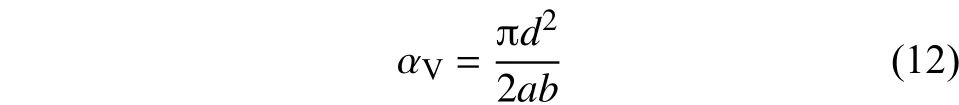
则基体所占的体积分数为[18]：

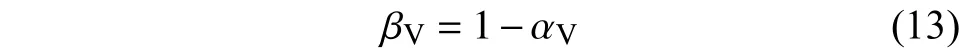
碳纤维所占的质量分数计算式为：

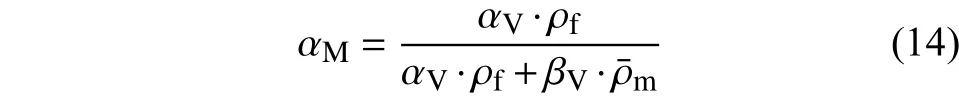
则基体所占的质量分数为：

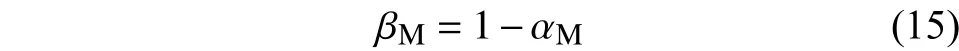
4 计算结果及分析

基于以上数理方程并借助于有限元软件COMSOL Multiphysics，对一种三维编织碳/酚醛复合材料在单侧热流加热下的热响应行为进行计算。计算过程中建立两种不同尺度的模型，其中，细观尺度模型采用了结构化网格，网格分布如图1所示；由于宏观尺度模型的结构相对复杂，对其采用四面体网格剖分并且单元增长率设置为1.2，获得的网格分布如图2所示。对于两种不同尺度的模型，均指定：材料结构的顶面（y = 10 mm）为加热面（heating surface），施加在此面上的边界条件应用方程（8）计算，加热热流qconv为405 kW/m2；顶面和底面对环境辐射的发射率分别为0.9和0.05；除顶面和底面外，剩余各侧面定义为绝热壁面。由于外界环境辐射进入材料的热量较小，因此计算中忽略了qrad-in对温度场的影响。计算过程中，使用的材料属性和热解反应的动力学参数分别如表1、表2所示，炭层的导热系数如图3所示。

4.1 纤维束

图4为加热过程中纤维束的导热系数和比热随温度的变化曲线，图5为其密度随温度的变化曲线。从图4和图5可以看出，在加热开始时各属性参数的变化较为平缓，当温度达到一定程度时各曲线由平缓过渡到剧烈变化。其中，导热系数随温度的升高而单调增加，这主要是因为加热过程中酚醛树脂热解炭化产生了炭层，炭层的导热能力比酚醛树脂的强（导热系数如图3所示），使得基体整体的导热能力增强，最终导致纤维束整体的导热能力也随之增强，表现为导热系数逐渐变大。

图2 宏观材料结构的网格剖分Fig.2 Mesh of macro material structure

表1 材料属性Table 1 Material properties

表2 热解反应动力学参数Table 2 Chemical kinetic parameters

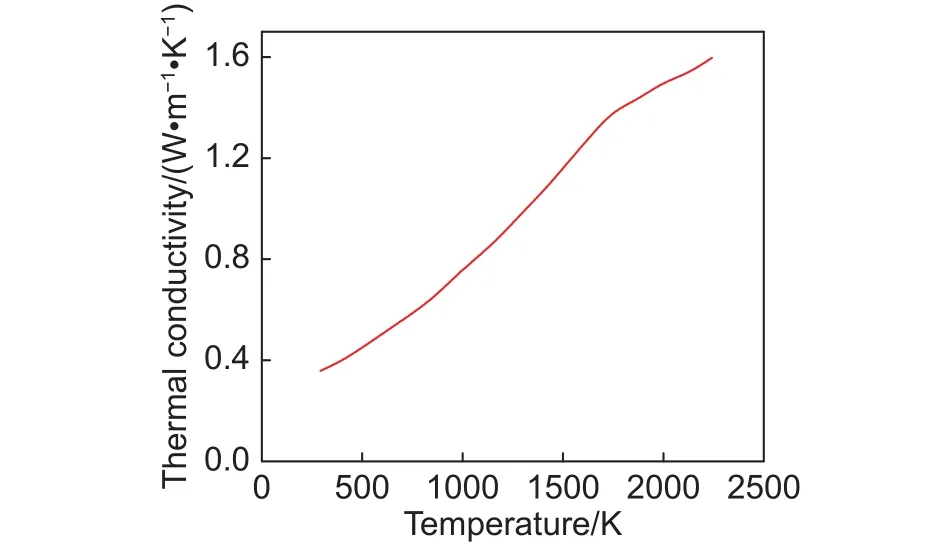
图3 炭层的导热系数Fig.3 Thermal conductivity of char layer

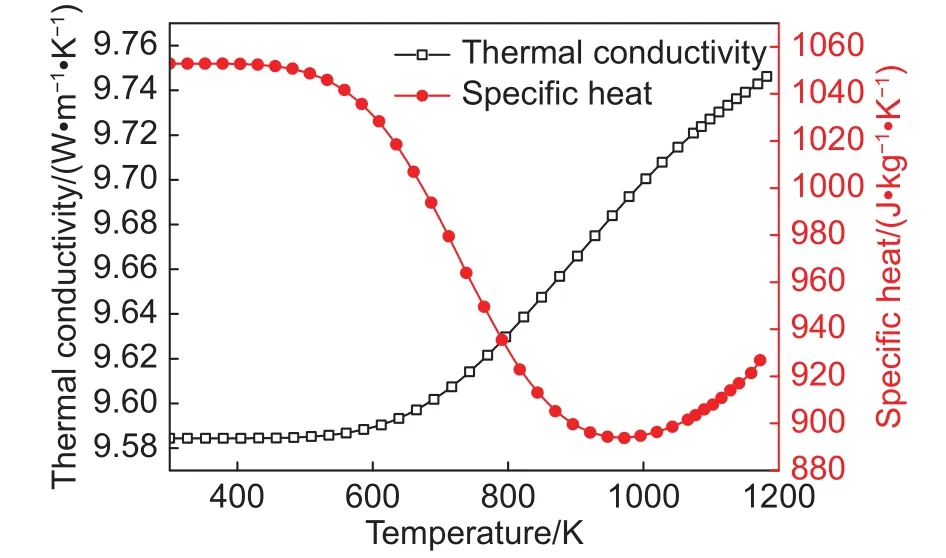
图4 纤维束的导热系数和比热随温度的变化Fig.4 Thermal conductivity and specific heat of fiber bundle as a function of temperature

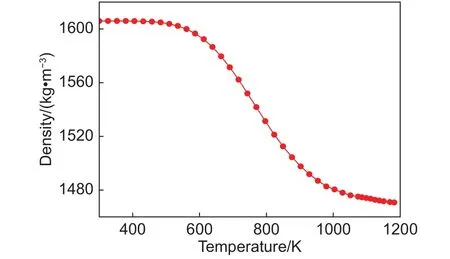
图5 纤维束的密度随温度的变化Fig.5 Density of fiber bundle as a function of temperature

另外还可以看出，导热系数升高的幅度并不大，整个加热过程中导热系数仅在0.17的范围内变动；与导热系数的变化趋势正好相反，密度随温度的升高呈单调递减，这是由于酚醛基体热解后产生的炭层密度较低，使得基体整体的密度出现衰减，从而导致了纤维束整体的密度出现递减的趋势；比热随温度的升高先减小后出现了小幅度的增加。产生这种变化趋势的原因为炭层的比热随温度的增加而增加，其变化规律在表1中给出。在一定的温度范围内，炭层的含量以及比热均处于相对较低的水平，此时的炭层不足以使基体整体的比热升高，基体整体的比热在此温度范围内逐渐较小，因而使得纤维束整体的比热随之减小；当温度继续升高，炭层含量以及比热随之增加。在温度达到一定数值时，此时的炭层含量和比热足以使基体整体的比热升高，基体整体的比热在此温度后开始逐渐增加，因而导致了纤维束整体的比热出现小幅度的升高。

4.2 复合材料整体

图6为加热过程中碳/酚醛复合材料整体和纤束维的温度场分布。由图6可以看出，随着时间的增加复合材料的温度随之升高，在顶面达到最大值1420 K，并且在材料的厚度方向上温度由顶而底逐渐降低，在30 s时上下面最大温差达到了1118 K。温升过程中，复合材料的温度场分布并不均匀，具有很大的温度梯度，这是由于复合材料的基体和纤维为异质体，两者的导热能力存在明显的差异。碳纤维的导热系数比酚醛基体的大，热量可以传递到更深的位置，因此出现了材料内部竖向纤维束的温度比基体的温度要高；而对于酚醛基体，其在加热过程中产生了表面炭层，该炭层导热系数小而比热较大，当在外界加热时炭层吸收了大量的热量从而对内部结构起到隔热作用，这样就形成了热量集中在材料的表层区域而较难传递到材料内部，因此出现了表层区域的温度比其他区域的温度要高。

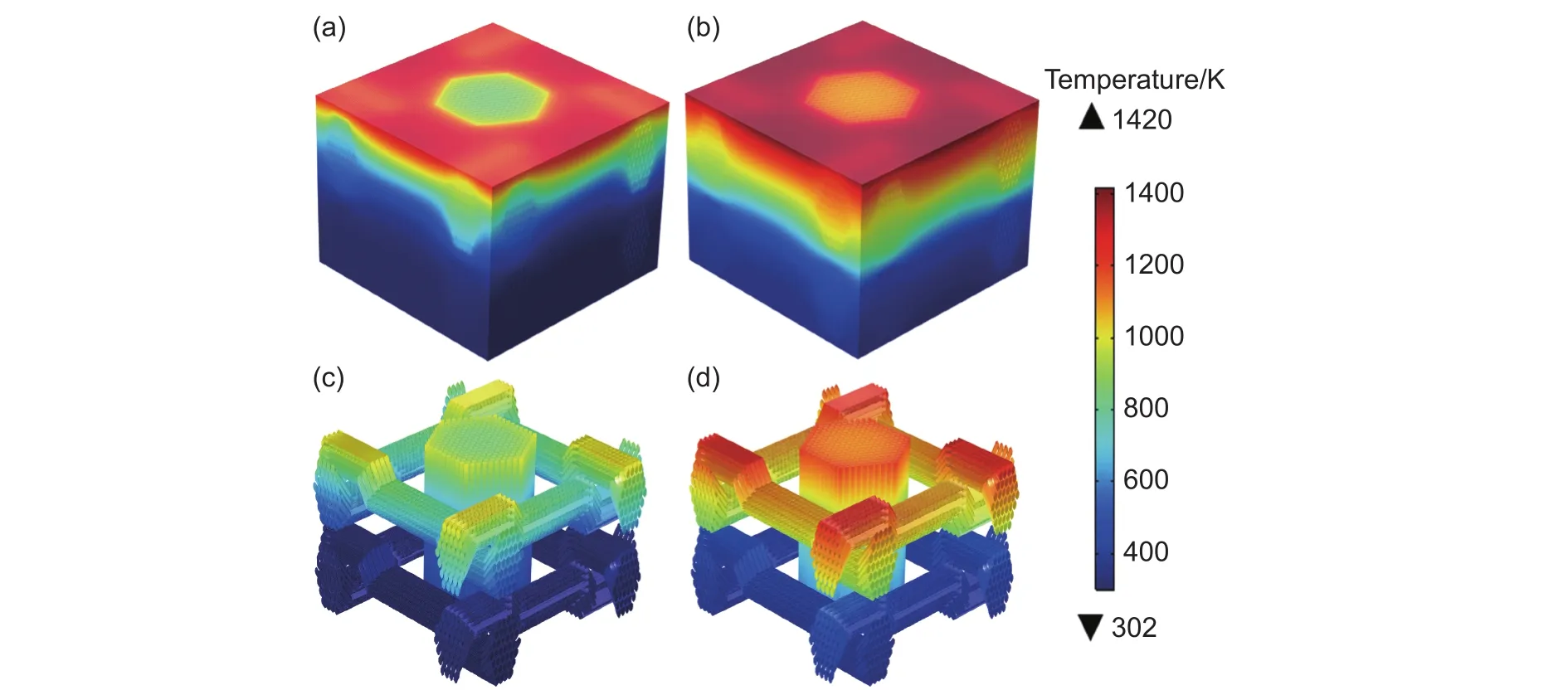
图6 碳/酚醛复合材料的温度分布（a）整体 15 s；（b）整体 30 s；（c）纤维束 15 s；（d）纤维束 30 sFig.6 Temperature distributions of carbon/phenolic composite （a）whole 15 s；（b）whole 30 s；（c）fiber bundle 15 s；（d）fiber bundle 30 s

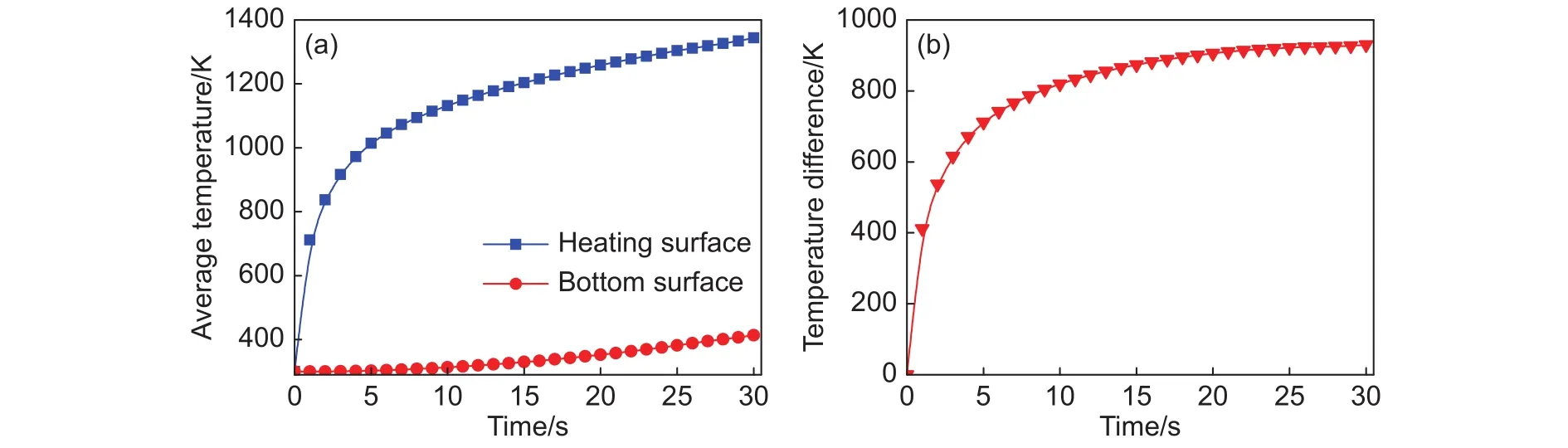
图7 复合材料面温度和温差随时间的变化（a）面温度-时间；（b）温度差-时间Fig.7 Surface temperature and temperature difference of composites as a function of time（ a） surface temperature vs time；（b） temperature difference vs time

图7 为顶面和底面的平均面温度和两者之间的温差随时间的变化曲线。由图7可知，在加热开始时，加热面的平均温度随时间的增加而迅速升高，在第 5 s时平均温度达到了 1014.3 K，而在这5 s的时间段内温度的增加值为714.3 K；随着时间的延长，加热面平均温度的温升速率逐渐降低，在第 30 s时平均温度达到了 1343.4 K，而在这 25 s的时间段内温度增加值为329.1 K，仅为5 s时间段内温度增加值的46%。这是因为，在加热开始时加热面温度较低，表面材料还没有进行充分的热解，由热解气体带走的热量和表面对环境的辐射热量均较小，因此在外界热流作用下加热面获得较多的热量，使得温度在短期内迅速升高；而在一段时间后，加热面温度达到一定数值，表面材料充分热解，由热解气体带走的热量和表面辐射损失的热量增加，因此加热面获得的热量减小，温升速率逐渐降低，最终加热面温度在外界热流、表面辐射散热、热解气体溢出带走热量的共同作用下将趋于平衡。材料底面的平均温度变化较为缓慢，在第30 s时温度值仅为412 K；加热面和底面的平均温度差随时间的变化与加热面平均温度的变化具有相似的规律，随着时间的增加平均温差保持在931K的温度范围内。

加热过程中最大温度和平均温度分别代表了复合材料产生的温度极值和材料整体的温度水平，图8为碳/酚醛复合材料的最大温度和平均温度随时间的变化曲线。由图8可以看出，复合材料整体的平均温度随加热时间的增加几乎呈线性变化。在30 s时，平均温度达到了743 K，而最大温度则达到1420 K，是平均温度的1.91倍；温度的最大值出现在加热面上，30 s时加热面的平均温度为 1343.4 K（见图 7），比此时刻的温度最大值小了76.6 K。

加热过程中，由于酚醛树脂的不断热解，基体密度出现衰减并产生了炭层，材料质量随着加热时间的延长而出现亏损。图9为碳/酚醛复合材料质量损失率随基体平均温度的变化曲线。由图9可以看出，质量损失率随基体平均温度的升高而迅速增加，在温度达到500 K后，复合材料的质量损失率几乎呈线性变化，在30 s时质量损失率达到了15.93%，可见加热过程中碳/酚醛复合材料出现了明显的质量损失。

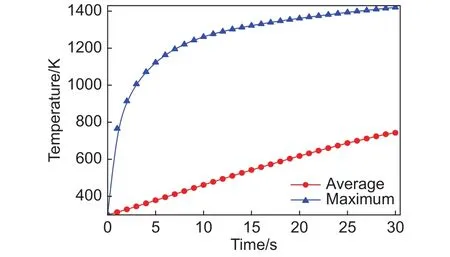
图8 碳/酚醛复合材料的最大温度和平均温度随时间的变化Fig.8 Maximum temperature and average temperature of carbon/phenolic composite as a function of time

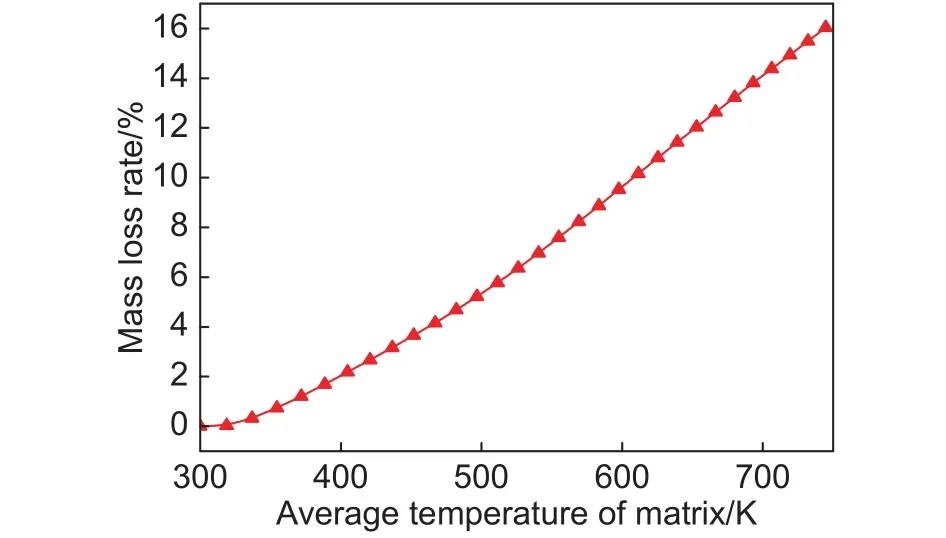
图9 质量损失率随基体平均温度的变化Fig.9 Mass loss rate as a function of average temperature of matrix

热解度反映了加热过程中基体材料热分解反应的强弱程度，其数值在0到1之间。0表示材料完全热解，1表示材料还未进行热解。图10为酚醛基体的热解度分布，由图10可知，加热过程中顶面温度较高材料首先发生热解，随着时间的推移，材料表面完全热解形成炭化层，并且热解层随着温度的传递而逐渐向厚度方向转移。除此外，还可以看出，酚醛基体的热解层实际上仅发生在一个很薄的区域内，材料的大部分区域由未热解（热解度为1或者接近于1）和热解完成（热解度为0或者接近于0）的材料所占据。

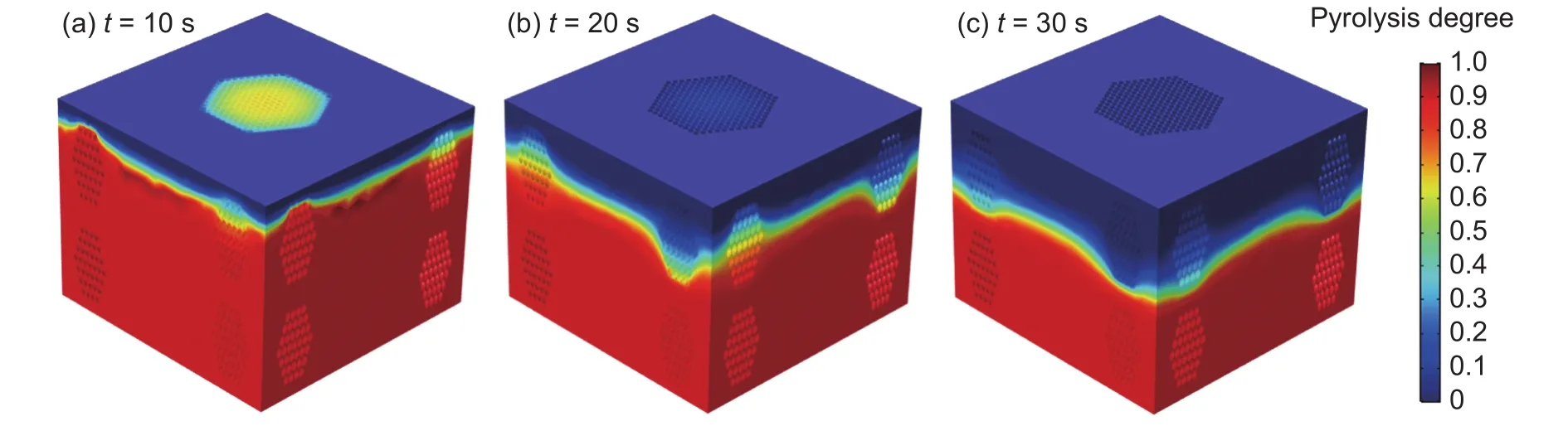
图10 酚醛基体的热解度分布Fig.10 Pyrolysis degree distributions of phenolic matrix （a）10 s，（b）20 s，（c）30 s

随着酚醛树脂的高温热解，材料被炭化产生表面炭层。一方面，该炭层的产生可以起到辐射散热的作用；另一方面，炭层还可以充当高温隔热层，对内部材料起到保护作用。因此，炭层的产生情况也是评价热防护材料防热性能的重要指标之一。图11为加热过程中炭层的生成位置。可以看出，炭层主要出现在顶端加热面附近区域，这是因为加热面上温度高，材料热解充分成炭率高。随着加热时间的延长，炭层厚度增加且向材料结构的厚度方向延伸。

图11 炭层的生成位置Fig.11 Formation position of char layer during heating process （a）10 s，（b）20 s，（c）30 s

图12 为平均炭层厚度随时间的变化曲线，由图12可以看出，炭层的产生需要一段时间的过渡，在此时间段内炭层厚度为0。这主要是由于，加热开始时表层基体材料出现热解，当热解度达到一定数值时才开始生成炭层，而要达到这一热解度需要一个很短的过渡时间。在此时间段后随着时间的继续增加炭层厚度迅速增加，在30 s时酚醛基体的平均炭层厚度达到了1.288 mm。