腐蚀条件下基于Gerber模型的DFR推导及实测

陈跃良,吴省均,刘 旭,卞贵学,张 勇,王安东,黄海亮,张柱柱

（海军航空大学 青岛校区，山东 青岛 266041）

细节疲劳额定值（detail fatigue rating，DFR）法是20世纪80年代波音公司针对大型民用运输机提出的一种简单可靠的疲劳分析评估方法[1-2]。类似于静强度校核方法，DFR法以疲劳裕度为指标检查结构是否达到设计寿命可靠性，容易被一般设计人员接受和掌握。DFR法能够在新机研制初步设计阶段对所有结构实施疲劳评估，减少了详细设计阶段对关键结构设计更改的情况，提高了结构设计的工作效率，对飞机结构的疲劳设计有着重要意义[3]。

传统DFR法计算公式是基于幂函数型S-N曲线和Goodman寿命曲线等推导的，适用范围为3.5 × 103～3.5 × 106次寿命区间[4]，但工程中疲劳寿命并不局限于此区间，而且上述寿命曲线也并不能表征所有材料/结构的疲劳性能。因此，何时能直接使用传统的DFR计算公式，疲劳设计能否兼顾经济性与耐久性以及采用Gerber模型能否提高DFR的计算精度仍需深入研究。

陈先民等[5]结合不同S-N曲线模型和等寿命曲线模型对传统DFR法进行了拓展，提高了DFR法在低周和超高周疲劳分析中的适用性。黄啸等[6]通过对DFR法的计算参数取值敏感性的研究发现，基于Goodman模型来计算延性材料的DFR值时结果偏于保守。樊俊铃[7]通过研究发现，对于铝合金材料，基于Goodman模型计算的DFR值比基于Gerber模型的小5%左右。

针对不同性能的材料选择合适的等寿命曲线模型，能够最大限度地发挥材料的潜能，降低成本；而且可以在满足结构可靠性的同时达到减轻重量的目标，这对于DFR方法的完善以及飞机总体设计具有重要意义。

为了研究等寿命曲线的选取对DFR计算结果的影响，本工作选取六种典型航空材料，对比Goodman模型和Gerber模型对于高周疲劳数据的拟合精度。针对2024-T3铝合金（表面阳极化）进行 0 h、6 h、12 h、24 h、36 h 和 72 h 的预腐蚀疲劳实验，对比基于不同等寿命曲线的DFR并对预腐蚀72 h的实验件进行断口分析。

1 等寿命曲线模型对材料高周疲劳数据的拟合

等寿命曲线目前常用的经验公式主要有以下几种：

Gerber抛物线模型

Goodman直线模型

因为直线模型比较简单又偏安全，因此工程上常用Goodman模型[8]。传统DFR法的计算公式就是基于幂函数型S-N曲线和Goodman型等寿命曲线推导得到。

从图1可以看出，对于TC4钛合金、30CrMn SiNi2A钢、16Co14Ni10Cr2Mo钢和 0Cr16Ni6钢，用Goodman曲线表征拟合精度更高。对于LD10CS锻造铝合金和LY12CZ航空铝合金，用Gerber模型则表征效果更好。

图1 六种典型航空材料两种等寿命曲线与实验数据的对比Fig.1 Comparisons of Goodman and Gerber equations with experimental data for six typical aviation materials（a）30CrMnSiNi2A （KT = 2）；（b） 16Co14Ni10Cr2Mo （KT = 2）；（c） 0Cr16Ni6 （KT = 2）；（d） TC4（KT = 3）; （e） LD10CS （KT = 3）；（f） LY12CZ （KT = 2.5）

因此对于脆性材料，DFR计算公式可以直接使用波音公司提供的公式，而对于延性材料，则需基于Gerber型等寿命曲线推导出新的计算公式。

2 腐蚀条件下基于Gerber模型的DFR 法

2.1 基于 Gerber 模型的 DFR 计算公式

幂函数S-N曲线表达式为：

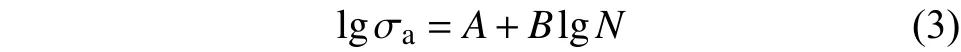
式中：S为材料常数。

置信度、可靠度为双95%的疲劳寿命N95/95=105次循环的等寿命曲线表达式为：

将式（4）式和（6）代入式（3）得：

由DFR 定义，当应力比R=0.06 且N95/95=105时，应力幅值和应力均值分别为0.47 DFR和0.53 DFR，代入Gerber型等寿命曲线可得：

将式（9）代入式（8）可得

可得基于Gerber模型的DFR表达式为：

2.2 腐蚀环境下基于 Gerber 模型的当量 DFR 的确定

假设腐蚀对结构件疲劳性能的影响完全反映为DFR的改变，腐蚀前后其他参数均不变[11-12]。设在一定的载荷状态下，结构件在无腐蚀条件下的疲劳寿命为，DFR为；腐蚀环境中的疲劳寿命为，当量DFR为。

化简为：

3 实验研究

3.1 试件

选取某型飞机常用材料2024-T3铝合金板材（表面阳极化），理论应力集中系数KT=1.5。主要原材料成分见表1，试件形式如图2所示。

3.2 预腐蚀疲劳实验

干湿交替是材料发生电化学腐蚀的重要原因。大量实验研究表明，采用周期浸润腐蚀方法可以很好地再现外场服役环境下金属材料出现的腐蚀损伤[13]。周期浸润腐蚀实验一个周期构成如下：首先在加入稀H2SO4的5%NaCl溶液中浸泡7.5 min，溶液 pH 为 4～4.5，温度为（40 ± 2）℃；然后在 40℃和90%～95%相对湿度的潮湿空气中，用远红外灯照射烘烤试件22.5 min。调节远红外灯的位置与功率，使试件在临近浸入溶液前被烘干，示意图见图3。预腐蚀实验设备为ZJF周期浸润腐蚀实验箱，疲劳实验的加载设备为MTS810电液伺服疲劳机。

表1 2024-T3 铝合金主要化学成分（质量分数/%）Table 1 Chemical composition of 2024-T3 alloy （mass fraction/%）

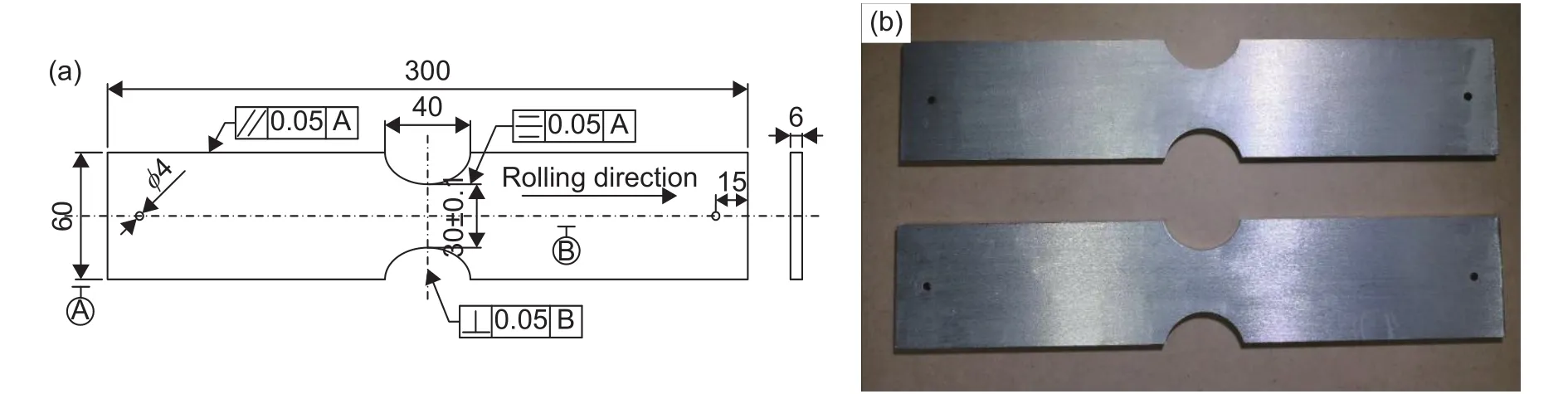
图2 2024-T3 铝合金试件 （a）试件尺寸；（b）试件照片Fig.2 Test pieces of 2024-T3 alloy （a） size of test pieces；（b） photo of test pieces

图3 预腐蚀实验谱Fig.3 Pre-corrosion test spectrum

3.3 断口分析

将预腐蚀72 h的试件疲劳断裂后，从夹具中取出并立刻包上薄膜。线切割切下断口，将其先后置于乙醇、丙酮中，用超声波清洗3 min后取出；自然干燥后用扫描电镜进行断口分析。

4 实验结果及分析

4.1 实验结果

将预腐蚀 0 h、6 h、12 h、24 h、36 h 和 72 h 的试件进行应力比 R = 0.06、正弦波形、载荷频率 10 Hz的疲劳实验。根据文献[14]提供的方法去除粗大误差后将结果列于表2，表中所有实验数据均满足标准HB 7710—1994 《金属材料细节疲劳额定强度截止值（DFRcutoff）实验方法》所要求的最小实验件数。将基于不同等寿命模型计算的DFR列于表3中。

计算结果表明，随着预腐蚀时间的增长，2024-T3铝合金的DFR先不变后下降。由于试件经过表面阳极化，较短时间的预腐蚀并不能破坏阳极膜，铝合金表面无点蚀坑，因此与未腐蚀试件的疲劳性能相比，没有明显变化。随着预腐蚀时间的增长，试件表面的阳极化膜被破坏，铝合金表面形成点蚀坑并且逐渐变深，材料的力学性能逐渐下降，所以DFR随着腐蚀时间的增长而降低。

根据文献[15]，在腐蚀环境中DFR随腐蚀时间的表达式为：

表2 2024-T3 铝合金不同预腐蚀时长下的疲劳实验结果Table 2 Fatigue test results of 2024-T3 alloy under different pre-corrosion durations

表3 基于不同等寿命曲线的 DFR 值Table 3 Calculation results based on different equal-life curves

式中：DFR0为未腐蚀试件的DFR值；n为拟合常数；t为腐蚀时间。

经过拟合得到DFR随腐蚀时间的变化曲线为：

拟合精度R2为0.80559，拟合曲线见图4。

图4 2024-T3 铝合金 DFRGerber 随预腐蚀时间的拟合曲线Fig.4 Fitting curve of 2024-T3 alloy DFRGerber with pre-corrosion time

文献[15]给出某些环境下无保护层试件DFR随腐蚀时间变化的表达式：

对于3.5%NaCl水溶液，适用于沿海大气环境：

对于卫生间下水道尿液环境：

将式（19）和式（20）中的 n 值与式（18）比较可见，经过阳极化处理的实验件在腐蚀环境中DFR下降速率较慢，这是因为表面的阳极化膜能够提高铝合金的耐腐蚀性。

4.2 基于 Goodman 模型和 Gerber 模型的计算结果比较

依据文献[6～7]，基于Goodman模型的DFR法对于延性材料的DFR计算结果较为保守，即应大于，但是本工作经过计算发现除了预腐蚀0 h情况外，其余情况均小于。进一步发现，越接近，两种方法的计算结果越接近，因此当时=。

因此，并不是在全寿命范围内基于Gerber模型的DFR法都能够发挥延性材料的潜能，在区间，

4.3 断口形貌

试件经过72 h预腐蚀后表面存在大量点蚀坑，这些点蚀坑一方面会造成应力集中，另一方面也会破坏局部材料的晶粒排列而造成材料疲劳性能的下降，因此点蚀坑不仅是潜在的裂纹萌生源，而且由于点蚀坑处的材料力学性能相对薄弱，裂纹扩展路径也往往会经过点蚀坑。图5为处于裂纹扩展路径上的一个点蚀坑。

除了蚀坑这一重要影响因素，夹杂物也会对疲劳寿命造成影响[16]。图6中颜色较浅的点状物是2024-T3铝合金中的夹杂物，对于同一类型的夹杂物，当尺寸分布相同时，疲劳寿命随夹杂物的增多而下降；但对尺寸分布不同的夹杂物，夹杂物尺寸的变化对疲劳性能的影响远大于夹杂物含量。因此，图中尺寸大于300 μm的点状夹杂物对材料的疲劳破坏具有严重的影响。另外从图6还能看出明显的台阶，说明疲劳断面并不是一个宏观平面，而是沿着一系列具有高度差的，寻求阻力最小的平面向前扩展[17]。

图5 2024-T3 铝合金腐蚀蚀坑Fig.5 Corrosion pits of 2024-T3 alloy

图6 2024-T3 铝合金腐蚀蚀坑、夹杂物和台阶Fig.6 Corrosion pits,inclusions and cleavage steps of 2024-T3 alloy

5 结论

（1）对于 TC4钛合金、30CrMnSiNi2A钢、16Co14Ni10Cr2Mo钢和0Cr16Ni6钢等脆性材料，可直接使用波音公司提供的DFR算式；对于LD10CS和LY12CZ铝合金等延性材料，则使用基于Gerber模型等寿命曲线推导的DFR公式，计算结果更为精确。

（2）经 0 h、6 h、12 h、24 h、36 h 和 72 h 预腐蚀后，2024-T3铝合金（表面阳极化）基于Gerber模型的DFR值分别为 84.251 MPa、84.721 MPa、79.683 MPa、80.745 MPa、77.026 MPa 和 74.996 MPa。随腐蚀程度增加，其 DFR值下降，变化规律为 DFR = 84.5211985.[lg（t+10）]–0.15578。腐蚀折算系数 CC分别为 1.006、0.946、0.958、0.914、0.890；表面阳极化可以提高该型铝合金的抗腐蚀能力，减缓DFR值的下降速率。

（3）当 N95/95＞ 105次时，基于 Gerber模型的DFR计算结果大于基于Goodman模型的计算结果，此时，基于Gerber模型的DFR法能够发挥延性材料的潜能。

（4）蚀坑会造成应力集中，加速疲劳裂纹的产生和扩展；2024-T3铝合金中尺寸大的夹杂物也会对材料的疲劳性能产生很大影响。