热环境中非保守简支-固支FGM梁的非线性力学行为
2019-04-15李清禄杨凡转张靖华
李清禄,杨凡转,张靖华
(兰州理工大学 理学院,兰州 730050)
为了适应航空航天应用的超高温材料,20世纪80年代中期,日本科学家引入了功能梯度材料(functionally graded material,FGM)[1]。FGM 是一类具有材料属性空间连续变化的新型复合材料,它能够承受高温梯度环境,而不会引起任何层间的分离。功能梯度材料通常由陶瓷和金属复合而成,其力学性能从一侧到另外一侧平滑和连续地变化,导致材料性质与等效物性参数也是梯度平缓变化,这使得FGM在航空航天结构以及聚变反应堆等领域得到了广泛的应用[2-3]。李斌太等[4]详细阐述了复合材料在航空领域的研究进展,指出建立复合材料国防科技实验室在航空装备领域的重要性。梁结构作为工程中常见的结构,因此有必要对FGM的各种力学性能进行研究,从而为结构设计及应用提供必要的理论依据。
Rahimi等[5]用Adomian分解法分析了具有一定倾斜角度的FGM悬臂梁在端部力作用下的大变形力学行为。Li等[6]研究了功能梯度Timoshenko梁和均匀Euler梁的屈曲载荷之间的关系。张大光[7]引入物理中面的概念,研究了双参数弹性地基上FGM梁的非线性弯曲问题。上述文献中的载荷都是横向保守载荷。崔宇等[8]通过研究指出,极端热环境对合金复合材料的微观组织和力学性能均有显著影响。李世荣等[9]考虑轴线伸长对梁变形的影响,研究了Timoshenko FGM梁在横向非均匀升温下的热过屈曲,讨论了非均匀升温对梁过屈曲行为的影响。Esfahani等[10]考虑了材料物性参数的温度相关性,研究了弹性地基上FGM梁的屈曲问题。李清禄等[11]研究了变厚度FGM圆板的热后屈曲问题,分析了材料梯度指数和厚度变化系数对圆板热后屈曲行为的影响。
在具体工程应用中,置于热环境中的FGM梁同时会受到机械荷载。工程中存在一种受结构的变形而方向发生变化的随从力,这种力显然是非保守力。例如,应用于航空航天的火箭和喷气式飞机均引起非保守力,这种非保守力将引起机翼的颤振。李清禄等[12]建立了Timoshenko梁在非保守载荷作用下的过屈曲控制微分方程,利用打靶法详细讨论了梯度指数,长细比等对梁过屈曲行为的影响。热载荷作用下FGM梁的力学行为也是研究的热点。赵凤群等[13]之后又研究了非保守力和机械-载荷下FGM梁的振动特性,利用小波微分求积法求解了数值解,讨论了梯度指数、温度等对一个简支梁的振动特性和稳定性的影响,但没有对温度环境下另外受到非保守载荷的FGM梁的屈曲或弯曲行为给出定性讨论。
相比之下,处于均匀和非均匀升温下,FGM梁受到非保守载荷非线性力学行为方面研究的成果极为少见。本工作基于轴线可伸长梁的大变形理论,通过一维热传导理论建立均匀和非均匀升温下FGM梁在随动载荷作用下的非线性力学控制方程;假设材料性质只沿梁厚度变化,建立温度场中FGM梁受到切线随动非保守载荷的大变形数学模型,采用打靶法将高阶偏微分方程化为两点边值问题的常微分方程实现数值求解;分析功能梯度材料梯度指数对不同温度环境下梁的非线性行为的影响。
1 FGM 材料的物性参数及其温度场
1.1 FGM 材料物性参数
考虑功能梯度材料梁为陶瓷和金属混合而成,梁的上表面为纯陶瓷,陶瓷材料的体积分数沿厚度方向为幂函数形式:
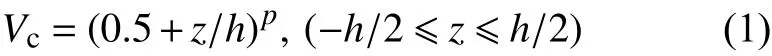
采用Voigt等应变的线性混合率模型,FGM材料的等效物性参数描述为:
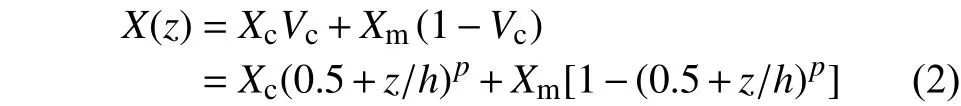
1.2 温度场
FGM材料通常服役于热环境中,记陶瓷一侧和金属一侧的温度分别为和,两侧温度都均匀分布,梁内温度沿厚度变化,取基础温度为。其中升温满足一维热传导方程及边界条件:
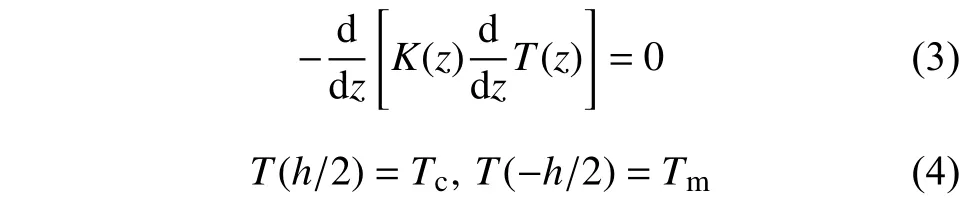
方程(3)在边界条件(4)下的幂级数形式的解为:
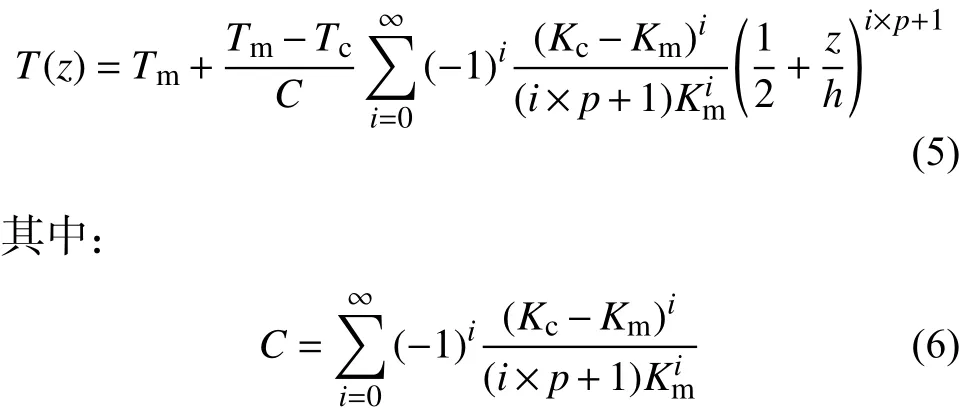
2 控制微分方程
考虑处于升温场中的FGM材料梁,其一端可移简支,一端固定。其中长为l ,矩形截面宽为,高为,假设梁上施加沿轴线均匀分布切向载荷作用(见图1)。梁在变形过程中,分布载荷的方向始终与轴线相切,即为随动载荷。
由文献[9]及[12]可给出无量纲形式的控制微分方程:
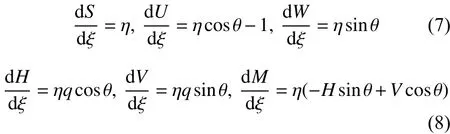
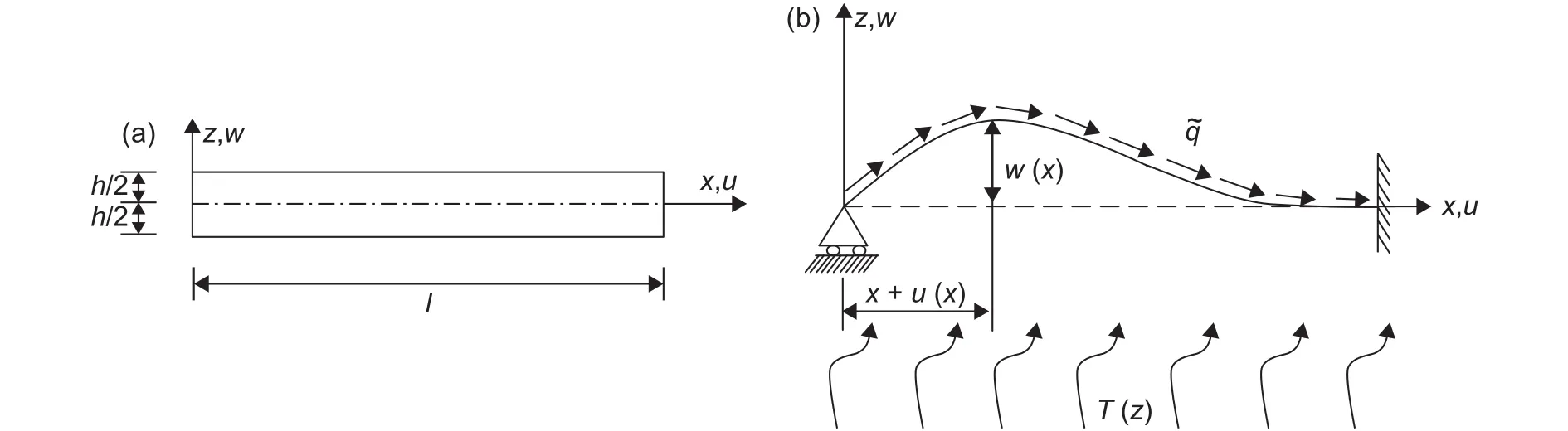
图1 升温场中受轴向随动分布载荷作用的功能梯度简支-固支梁 (a)功能梯度梁示意图;(b)力学变形模型Fig.1 A hinged-fixed FGM beam subjected to uniformly distributed follower forces in thermal environment ( a) schematic sketch of a FGM beam;(b)mechanical model of the deformed beam
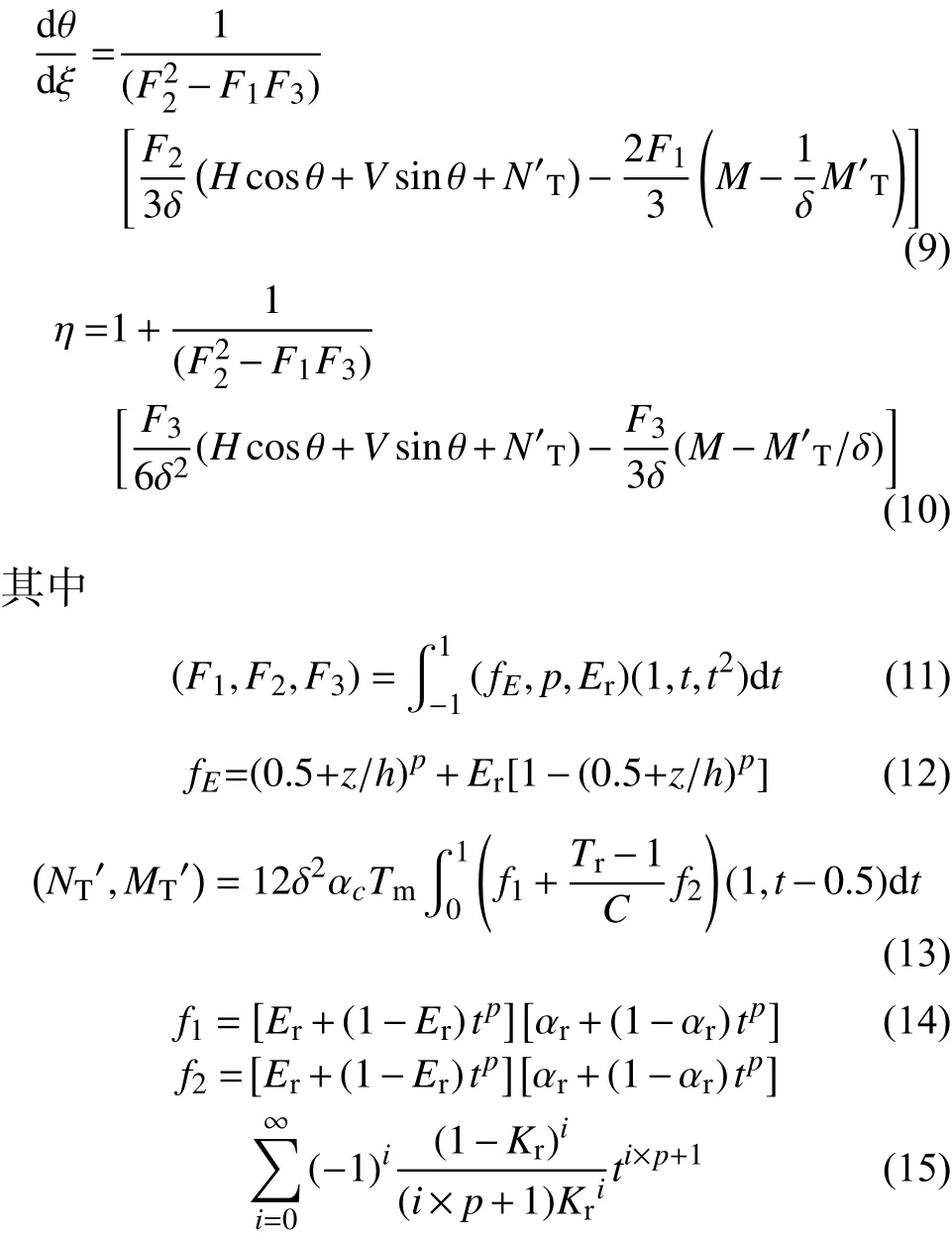
上述方程的无量纲量变换如下:
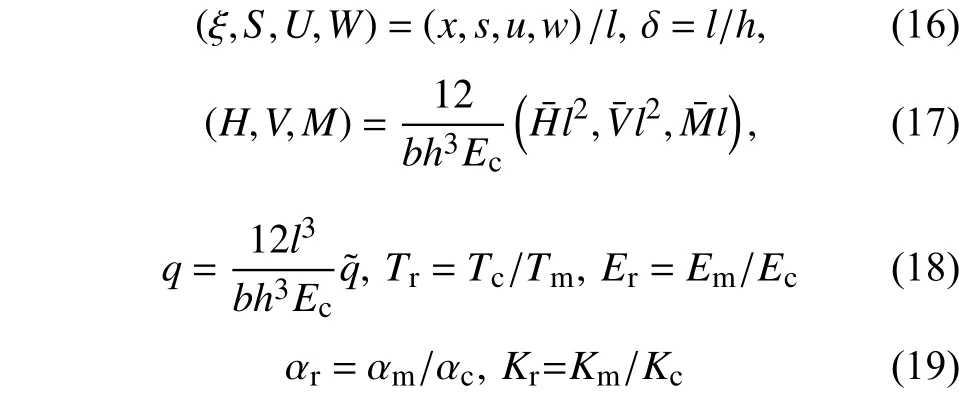
对图1所示一端可移简支、一端固定梁,相应的无量纲边界条件为
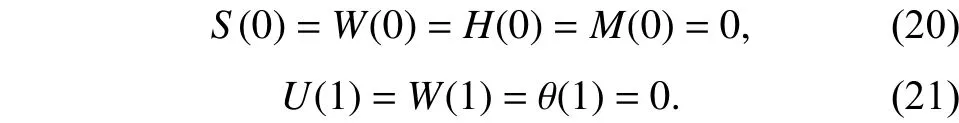
3 数值模拟及讨论
3.1 打靶法
由于式(7)~(10)是相互耦合的强非线性方程,很难获得解析解。这里采用打靶法[14]求其数值解。为此,将式(7)~(10)以及边界条件写成下式:

其中
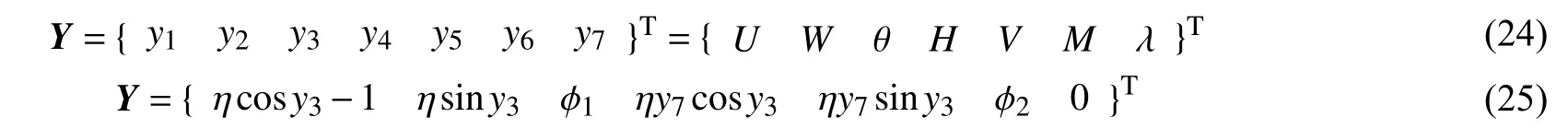
给定随从载荷时λ = q,矩阵B0、B1,向量b0、b1以及函数ϕ1、ϕ2的具体表达如下:
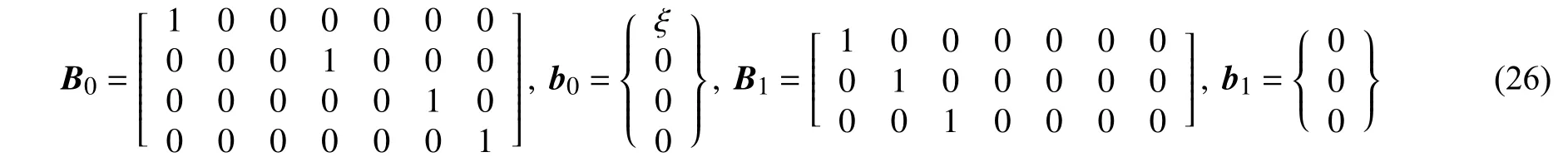
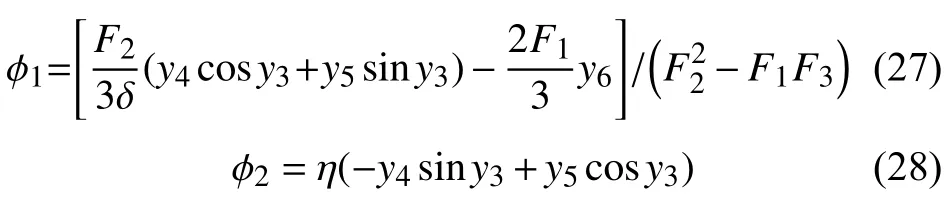
下面考虑一个与边值问题相对应的初值问题:
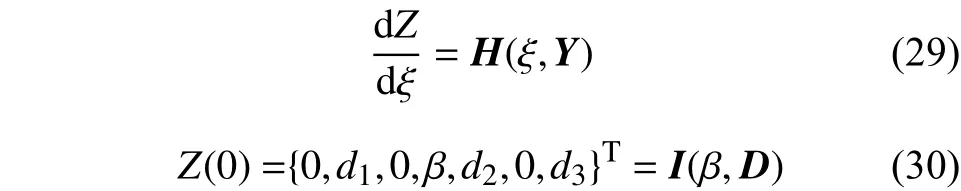
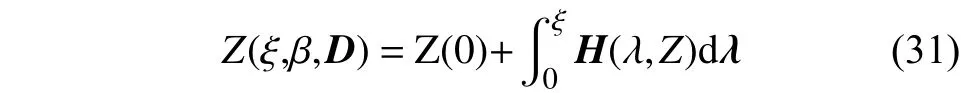
3.2 数值结果及讨论
考虑由陶瓷二氧化锆(ZrO2)和金属钛合金(Ti-6Al-4V)制成的FGM材料梁。两种材料的物性参数见表1。
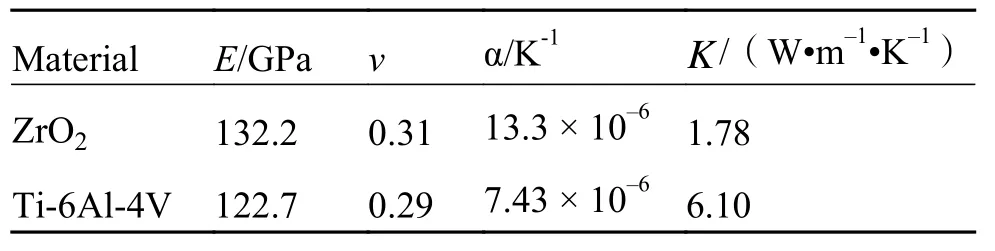
表1 陶瓷 ZrO2 和钛合金 Ti-6Al-4V 的材料系数Table 1 Material parameters of ceramic ZrO2 and titanium alloy Ti-6Al-4V
首先,为了说明打靶法的精确性和计算结果正确性,将功能梯度材料退化为均匀材料的结果和已知文献作了比较,其临界载荷,和已知文献[15]给出的结果完全吻合,说明了打靶法在本工作计算中的适用性。
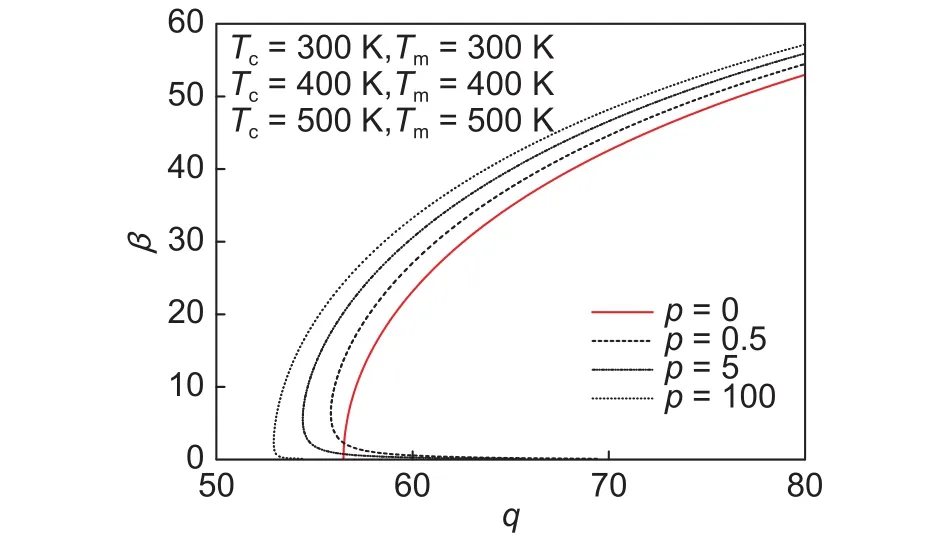
图2 左端转角与载荷的关系Fig.2 Relationship between left rotation angle and load
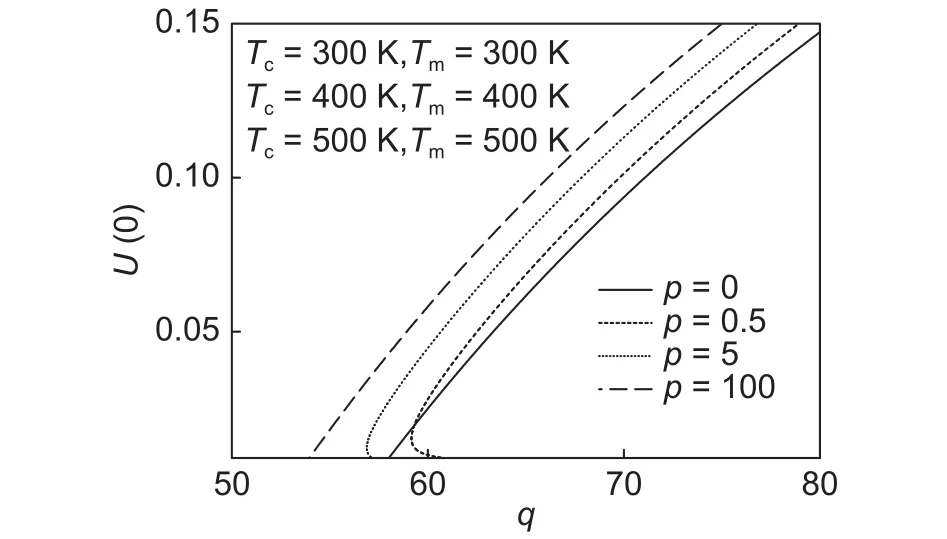
图3 左端位移 u(0)与载荷的关系Fig.3 Relationship between left displacement u(0) and load
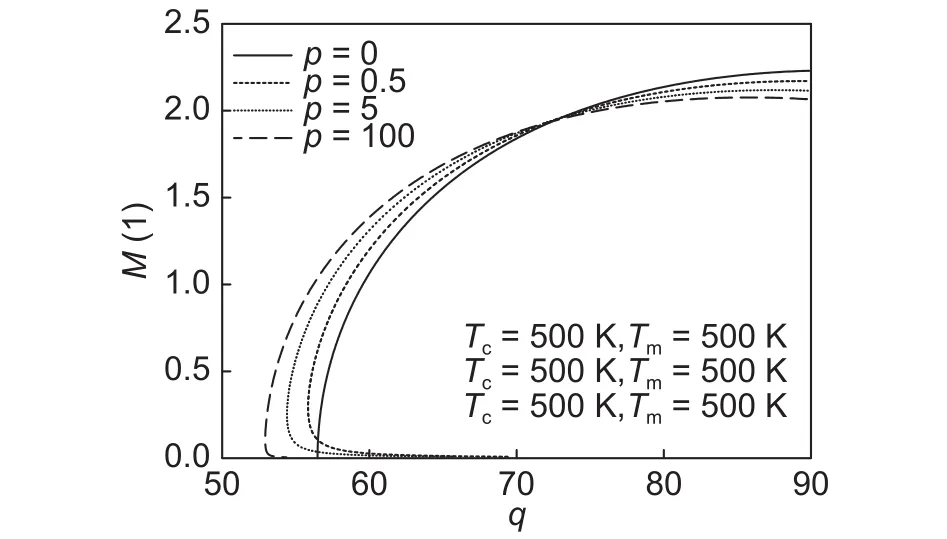
图4 右端弯矩 M(1)与载荷的关系Fig.4 Relationship between right end bending M(1) and load
图5 ~6给出了热轴力和热弯矩随材料梯度指数变化的曲线图。可以看出,热轴力随梯度指数的增加而单调递减,当之后,热轴力的减小趋于缓慢。而时热弯矩随梯度指数增大而增大,当之后,热弯矩又随梯度指数增大而减小。在相同的梯度指数下,随上下表面非均匀升温的增加,热轴力和热弯矩都增加。
为了考察不同非均匀升温下,载荷与各物理量之间的关系,图7~9给出了材料梯度指数情况下,、以及的关系曲线。显然,在均匀和非均匀温度场中,、以及是载荷的非单调非单值函数,这和无温度场作用下获得的结论是不同的。另外,随着上下表面温差的增加,变形相同的、、下需要的载荷较小,而在给定载荷时,、、先增加后减小。
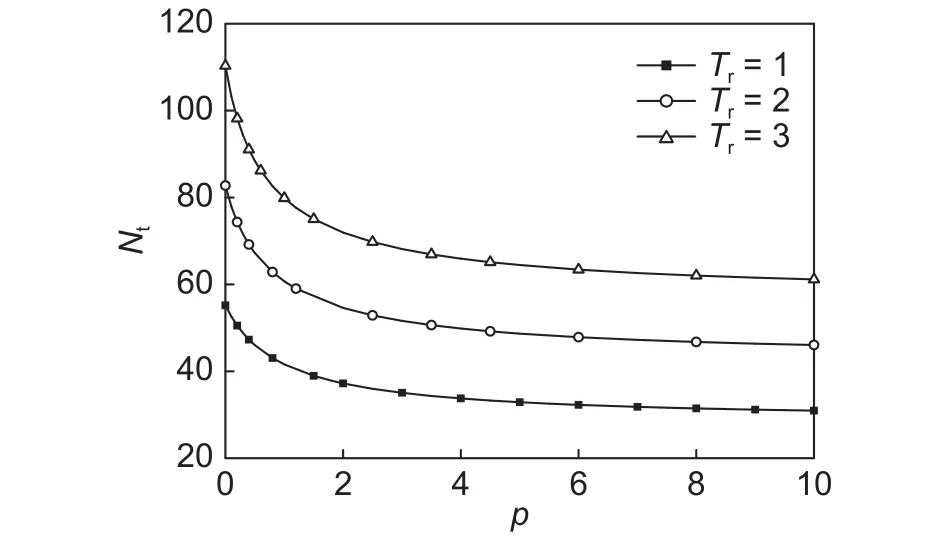
图5 热轴力 Nt与梯度指数的关系Fig.5 Relationship between thermal axial force Nt and gradient index
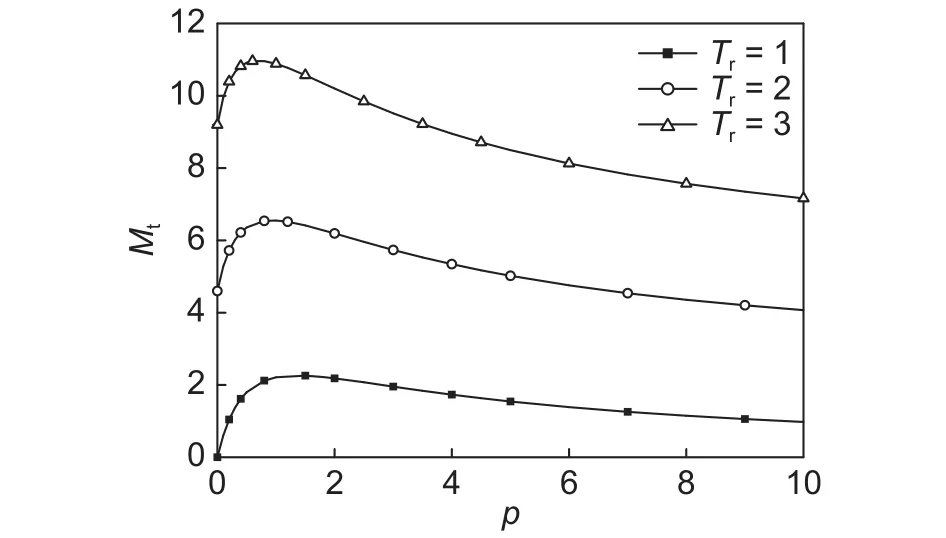
图6 热弯矩 Mt 与载荷的关系Fig.6 Relationship between thermal bending moment Mt and gradient index
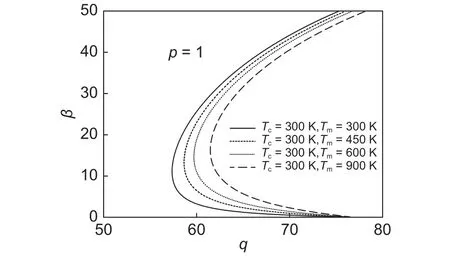
图7 非均匀升温下-的关系Fig.7 Relationship between and under non-uniform heating
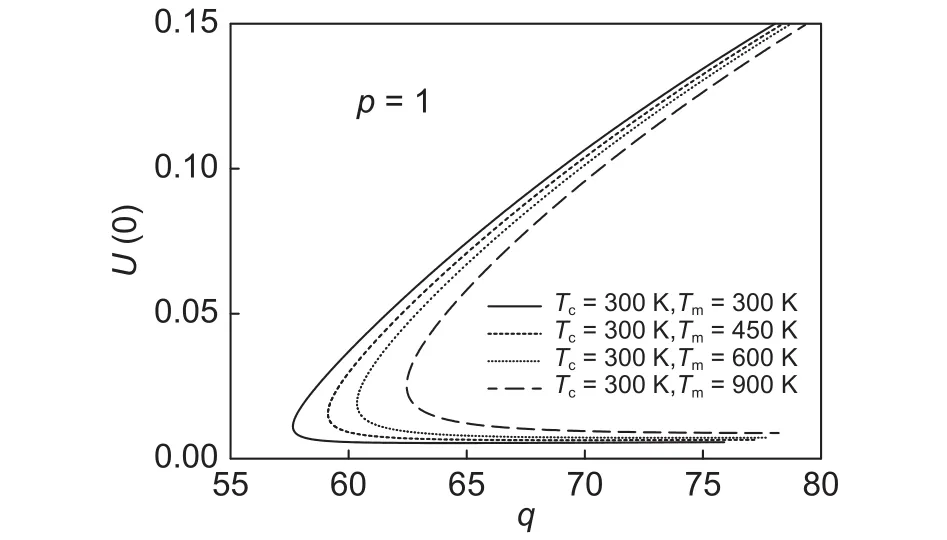
图8 非均匀升温下的关系Fig.8 Relationship between and under non-uniformheating
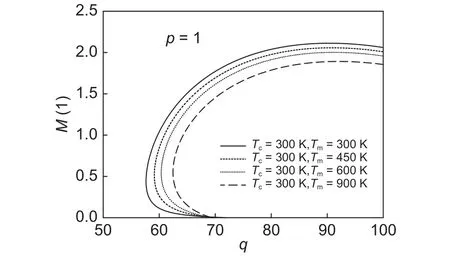
图9 非均匀升温下的关系Fig.9 Relationship between and under non-uniform heating
4 结论
(1)温度环境下非保守简支-固支陶瓷均匀材料梁发生典型的过屈曲行为,而相同条件下FGM梁发生非线性弯曲行为。
(4)在均匀和非均匀温度场中,位移和梁端内力是载荷的非单调非单值函数,而在无温度场作用下是单调单值函数。
