开方术与多个正根方程：从“可知”到“不可知”*

段耀勇,周 畅,段垒垒,孙青辉

(1.中国人民警察大学,河北 廊坊 065000;2.西安邮电大学 理学院,陕西 西安 710121;3.济南市长清区第二实验中学,山东 长清 250300)

0 引言

刘益之前,除赵爽勾股圆方注的二次方程是二正根外,其他所有开带从平方和立方皆只有一个正根.刘益之后,多正根方程逐渐增多.秦九韶、李冶对于多正根方程只给出一个,并给出选择的理由.杨辉、朱世杰都注意到方程开得的两个正根都有用,是列二次方程分别得出这两个正根的.汪莱最先指出对秦九韶和李冶“不可知为可知”的错误.从此多正根的方程即“不可知”首次进入中算家的视野.李锐时代,则采用降阶方程方法,即代开法求其他正根.随后,华蘅芳把素数的概念引入正负开方术在《开方别术》中所创立的数根开方术,是利用素数(早期译为数根)概念给出整系数方程有理根的方法,独具新意.[1]但是实际上就多个正根的方程而言,基于新步法的“正负开方术”是求解方便且计算效率高的方法.

1 巧合还是人为：只有一个正根的方程

1.1 开方术与高次方程的求解

开方术从一开始就是用来求解高次方程的根而产生的,从《九章算术》开方术开始,经刘徽改进,之后宋元又历经增乘开方、立成释锁和增城开方并存的时期,到正负开方而趋于完善.后来,明朝和清朝初期正负开方术已无人会用,取而代之的是珠算和立成释锁开方.李锐时代,中算家们才重新捡起正负开方法,并对高次方程的求解问题进行了研究得到了诸如笛卡尔符号法则、[4]韦达定理等一些方程论方面的结论.因为这些结论是在中国传统的开方术的基础上水乳交融,因此也表现出独特数学文化上的一种张力.

中国的开方算法开始就和解高次数字方程一体共生,基于增乘开方法,正负开方成为解高次方程的有效算法.《九章算术》开方算法已经可以很好地解决开平方和开立方的问题,但方法略显复杂,开立方表现尤为明显.三次以上的开方问题在《九章算术》中没有涉及.另外《九章算术》开方算法中只有一个系数均为正的开带从方开方问题,而且没有给出演算过程.经过南北朝的混战和短暂的隋朝后,迎来了盛唐时期,此时解决了大量的开带从立方的问题.开方已发展到开任意次方,或者方程次数可任意高以及系数符号无限制.宋朝出现的“立成释锁”和“增乘开方法”彻底解决了这个问题,并在宋元出现了列出这些高次方程的简便方法：“天元术”和“四元术”.此时的正负开方算法,是一种解决一元高次方程的一个正实数根的有效方法.

1.2 巧合还是人为：方程只有一个正根

刘益在北宋是极为重要的数学家.在杨辉于公元1274年成书《乘除通变本末》之前,刘益完成《议古根源》一书.刘益之前,所有开带从平、立方皆只有一个正根,即几乎所有的方程恰好只有一个正根,这不知是巧合还是人为抑或是算法本身的局限所致.随着生产实践和社会生活非常复杂,反映在与之相关的中国传统数学的结构里就是方程次数的提高,方程由二次变成了三次或者更高次.

《九章算术》的二次方程x2+34x=71000,其只有一个正根250,另一个根是-284.《缉古算经》中三三个根中正根为31,另外两个是负无理根.

刘益的书中大都是二次方程,只有一个四次方程：-5x4+52x3+128x2=4096.此方程实际上有两个正根：一个是4,另外一个是正的无理根,刘益只给出了一个正根.当然,若中算家想求这个正无理根,在方法上没有问题.因为开方术解高次方程时不区分正的有理根和正无理根.中国传统数学只处理方程的正根,正根分为整数、小数(或分数)和无理数三类.方程有非整数根时,中国古代数学家称之为“开根带奇零”,方法有“命分法”“续开法”(即刘徽的“求微数”)和“之分术”三种.其中“无理根”有两种方法,“命分法”得到无理根近似值的分数形式,“续开法”得到无理根近似值的小数形式.对于有理根也有两种方法,“续开法”得到“小数”形式的近似值,而“之分术”可以得到“分数形式”的准确值.[2]

对于这个有两个正根的方程,刘益只给出了第一个正整数根.而多正根方程,这种不和谐的声音在刘益之前就已初露端倪.

2 不和谐的声音：两个正根的方程

(1)赵爽二次方程求解的隐喻.三国时期的数学家赵爽,在其所著的《勾股圆方图注》中已隐含着一元二次方程有二正根及其根式解法.[3]当然这个解法是借助几何图形给出的.“倍弦为广袤合,令勾股见者自乘为实,四实已减之,开其余,所得为差,以差减合,半其余为广.”相当于给出二次方程x2-2cx+b2=0的根式解,先开得第一个正根c-c2-b2.“减广于倍弦,即所求(袤)也”,得另一个正根x2=2c-x1=c+c2-b2.此类有两个正根的二次方程,是借助开方术先求出一个,再利用两根间的关系算出另一个.赵爽并没有意识到这两个根属于同一个方程.刘益之后,多正根方程逐渐增多.

(2)刘益与杨辉的视而不见.北宋数学家刘益的《议古根源》中有两个题目：-x2+60x=864和-x2+60x=864.两者实际上是一个题目,刘益分别采用“益积术”和“翻积法”将他们看作两个方程,分别得到正根24和36.这里,同一个二次方程可以有两个正根的结论显而易见,但鉴于中国传统数学的特点以及中国用开方术解方程的独特性,这样的结论就不那么显然了.这两个题目见于杨辉的《田亩比类乘除捷法》,所以杨辉对此问题的认识同于刘益,对于一个二次方程两个正根,要处理成两个题目并用不同的开方技巧分别求出来.

(3)秦九韶和李冶的不选之择.南宋数学家秦九韶《数书九章》中的 “尖田求积”题目中处理了一个四次方程,并用正负开方术求得此方程的一个正根840.实际上-x4+763200x2-40642560000=0有四个实数根,即±240和±840.此题也可以通过试得第一位商为200,用正负开方术得到第二个正根240,此根不符合题意,但秦九韶并未对其选择840的原因做出过解释,或者没有意识到有两个正根.同样的,李冶《测圆海镜》卷三第五问的方程x3-336x2+5184x+2488320=0,有两个正根,即“半径”为120和288,但是李冶只给出“直径”值为240的答案.实际上此解三次方程的三个根分别是x1=120,x2=288,x3=-72.

至此,中算家只关注高次方程的一个正根已成为现实.清朝的数学家孔广森对一个根的方程进行了分类研究,他对3次方程和4次方程进行了归纳,他给出的13种形式是有正根的三次方程的全部形式,无重复无遗漏.所有方程都有一个正根12,可见上述工作是构造性的工作,是理论研究的结果.类似的还罗列出了4次方程的情形,也是只有一个正根的方程,这些方程都是用“立成释锁”求解的.

3 开方术的困境：多正根方程

中国传统数学的开方和解数值方程是同一个问题.开方nA,即求解xn=A,开带从方即求高次方程a0xn+a1xn-1+a2xn-2+…+an-1x+an=0,a0≠0,an＜0的数值解.求这两类方程的数值解的开方法和开带从方法,由《九章算术》的传统开方经过“立成释锁”,最终发展为一种很有效的增乘开方法.但是,因为中国传统数学更加强调其实用性,这种方法求解高次方程时有很大的局限性,增乘开方法出现之前这种情况更加突出.通常只求高次方程的一个正数根,遇到正无理根就用“命分法”或“求微数”的方法求出其近似值.另外,尽管中国负数的发现和应用是最早的,可是解方程却一直局限于求一个正根,没有考虑过负根,也没有讨论过方程根的个数和次数的关系以及根和系数的关系.

《议古根源》中相邻两个问题的答案刚好就是同一个一元二次方程的两个根,可惜的是刘益和杨辉都没有注意到这一点.也正是这种局限,使中国传统数学的方程论知识发展缓慢,直到清朝中期,汪莱才将有一个正根的方程称为“可知”,有多个正根的方程称为“不可知”,有一正根或多个正根者称为“可知”或“不可知”,才取得了一些成果.此时,多个正根的方程的多个正根才进入了中算家的视野.在《衡斋算学》第二册中,汪莱指出了有两个根的三次方程.汪莱以此为起点,指出x(p-x)2=q,p＞0,q＞0,0＜x＜p有两个符合题意的正根,而且这一发现成为清朝开始研究方程的起点.

从可知到不可知.汪莱是第一个认识到高次方程不止只有一个正根事实的人,这在中国数学史上是个突破.通过对秦九韶《数书九章》和李冶《测圆海镜》的研究,汪莱指出了秦九韶和李冶“以不可知为可知”的错误.之后,汪莱讨论了有实根的二次方程和三次方程正根的个数问题,无正根的情况不讨论.其研究成果在《衡斋算学》第五册中,书中按照方程的系数分类共列举了96条.他指出有实根的二次方程和三次方程共23个,16个有正根,无重复无遗漏.其中可知者9个,可知或不可知者1个,不可知者6个.如他给出a,b,c,d＞0时,ax3-bx2-cx-d=0可知,即有一正根;ax3-bx2+cx-d=0可知或不可知,即有一正根或多个正根;ax3-bx2+cx+d=0不可知,即无正根.这16个方程对二次和三次方程来说,无重复无遗漏.

认识到高次方程可能有多个正根,无疑在中国数学史上是个突破.但是对于不可知方程,如何求出这多个正根,对用开方术解方程来求解高次方程的中算家来说是个巨大的挑战.此前中国古代所有的高次方程也只求出了一个正根,这些高次方程包括可知方程和不可知方程,但在基础上如何求出不可知方程其他正根就是很大的问题了.

4 创新的局限：“代开”与“别术”

由于大多数方程都具有实际背景,所以中国古代解方程往往以得出一个正根即告完成,对于方程多根、正根则疏于讨论,汪莱在研读宋元算书时最先发现了这个问题.秦九韶的《数书九章》和李冶的《测圆海镜》中许多题目都不止一个正根.前文已论.宋元时期创立了正负开方术原只用于求解方程的一个正根.汪莱和李锐通过新发现进一步促进了正负开方术的发展,其中李锐的代开法和华蘅芳的数根开方法就是代表.李锐用降阶方程求其他正根,计算简单,但思维负担重且不易操作.后来华蘅芳利用素数的概念创立“开方别术”求解很有特色,如果正根不是整数,诸如是无理数根和分数根时此方法失效,文章不论此法.

李锐代开法.李锐代开法分为“寄位代开”和“较数代开”两种.其方法是在求得方程的一根后以递降一阶的方程求原方程的其余实根,这里介绍一下“较数代开”法.

较数代开法曰：“以本乘方先开一数.讫,变之,以递降一乘代开之,所得为较数,以较数加减(同名加,异名减).先得数为又一数,”并释在下,“凡立方可开三数,先开一数,讫.变之,验其所变之数,若可开二数则先开数为第一数,若可开一数则先开数为第二数,若无数可开,(谓无正数可开),则先开数为第三数.他皆仿此.”[5]

对于方程x3-151x2+2838x-14040=0,[6]求得130、12、9三个正根为例.首先估得初商100,即,此时开得第一个根的第一位数为100.

1 -151 2838-14040 100 100 -5100-226200 1 -51 -2262-240240 100 4900 1 49 2638 100 1 149

即f(x)=(x-100)3+149(x-100)2+2638(x-100)-240240=0.继续开方商得第一个根的第二位30.

1 149 2638-240240 30 30 5370 240240 1 179 8008 0

即(x-130)((x-100)2+179(x-100)+8008)=0,后面继续计算：

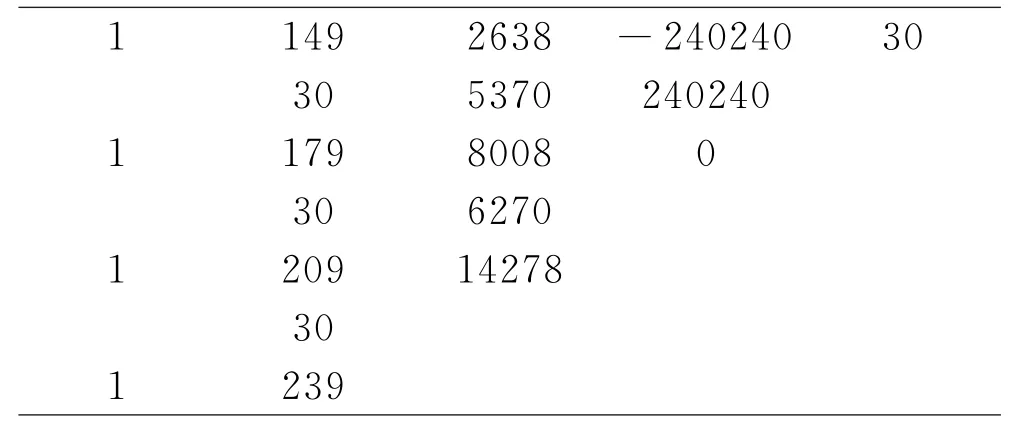
1 149 2638-240240 30 30 5370 240240 1 179 8008 0 30 6270 1 209 14278 30 1 239

可得f(x)关于(x-130)展开式即(x-130)3+239(x-130)2+14278(x-130)=0,此时,已经得到了方程的第一个根130.

对于(x-130)2+239(x-130)1+14278=0,令y=x-103,得y2+239y2+14278=0.开方：

1 239 14278 -100-100-13900 1 139 378-100 1 39 1 39 378 -10-10 -290 1 29 88-10 1 19 1 19 88 -8-8 -88 1 11 0-8 1 3

可得(y+118)2+3(y+118)=0,即(y+118)(y+118+3)=(x-130+118)((x-12)+3)=0

于是可得方程的另外两个根12和9,其中-118和-3称为较数.代开法的建立,使得正负开方术成为求解方程实根的一般方法,与寄位代开相比,较数代开更为简明.

5 回归与出路：正负开方术求解多个正根的方法

正负开方是一种解决一元高次方程的一个正实数根的有效方法,但在李锐前没有求多个正根的方程的方法.李锐“代开法”之前需要步根,即步法“凡平方可以开两数者,以正商步负实,得第一数,小数也.以负隅步正方得第二数,大数也.立方可开三数者,以正方步负实,得第一数,小数.以负廉步正方,得第二数,中数.以正隅步负廉,得第三数,大数.它皆仿此.”[3]此“步法”是用来估计正根位数和兼估商(第一位)的作用,在此基础上李锐用“代开法”求出这多个正根.既然已经步出了方程正根的个数和每一个根的第一位数,用“正负开方术”是求解方便且计算效率高的方法.下面以有两个正根的二次方程来说明这种方法的操作流程.

对于x2-60x+864=0,显然x1=24,x2=36.利用李锐的“步法”,即“隅步廉”得大正根36,“廉步实”得小正根24.

从上面李锐的两个例子也不难看出,这种方法具有一般性,所以他说：“它皆仿此.”即在开方式当中,自最下面的“隅”开始,从下至上用xn的系数“步”xn-1的系数开方：x的系数“步”x0=1(常数)的系数得最小的正根,x2的系数“步”x1的系数得次最小的正根,依次类推.

李锐以前都是用“方步实”,所以对于只有一个正根的方程没有问题,多个正根的方程只会得到那个相比而言最小的正根.李锐的“步法”为多个正根方程提供了用“正负开方术”求解的方法,尽管其本意是用步法来确定方程根的位数以及第一位数值.

综前所述,李锐所给的“步算”算例,开方只有一步,尽管有大小不同的根,但是只是在说明“步法”,即用“正负开方术”进行演算验证.这里“步法”的作用有两个：其一,估计正根的位数,是一位根还是多位根;其二,兼有估商的作用.但是,李锐的“代开法”无论是“寄位代开”还是“较数代开”,都不是特别简单,计算效率并不高,需要用“步法”讨论根的个数及其初商的大小.既然得到了每个正根的初商,直接用正负开方求得各个正根,反而更加简单和有效.