基于真隶属度的λ水平集的Vague集间模糊距离定义

周爱丽

（天津职业大学，天津 300410）

一、引言

自从Gau 和BuehIer 于1993年提出了Vague 集的概念后，学者们在理论和应用方面对它的研究一直同步进行。迄今为止，学者们对Vague集的研究主要集中在以下三个方面：①Vague 集(值)之间的相似度量（包括距离）；②基于Vague 集的决策方法；③Vague集理论的应用。

在很多时候，距离能方便地表达两个对象之间的区别。Vague 集(值)之间的相似度量可以根据Vague 集(值)之间的距离来定义。目前定义两个Vague 集(值)之间的距离有多种方法，如海明距离、欧氏距离、基于Hausdorff 测度的距离等。但几乎没有哪个距离公式能处理好所有Vague集之间的距离，同时其距离公式是建立在经典距离公里基础上的。本文基于这样的理念：Vague集是模糊的，Vague集之间的距离也可理解为模糊概念，即Vague 集之间的距离用模糊值表征更加符合实际。为此本文尝试提出Vague集之间的模糊距离定义。

二、预备知识

定义2.1 设U是论域，它的元素用x表示.U上的一个Vague 集A是指U上的一对隶属函数tA和fA， 即满 足0 ≤tA(x)+fA(x)≤1，其中tA(x)称为Vague 集A的真隶属函数，表示支持x ∈A 的证据的隶属度下界；fA(x) 称为Vague 集A的假隶属函数，表示反对x ∈A 的证据的隶属度下界；称πA(x)=1-tA(x)-fA(x)为x相对于A的犹豫度，πA(x)值越大，说明x相对于A的未知信息越多．将Vague 集A简记为

定义2.2 设x ∈U，称闭区间[tA(x),1-fA(x)]为Vague集A在点x的Vague值.

Vague值同时表示了支持、反对x ∈A 证据的隶属程度及未知程度.例如，A在点x的Vague 值为[tA(x),1-fA(x)]=[0.5,0.8]，则有tA(x)=0.5，

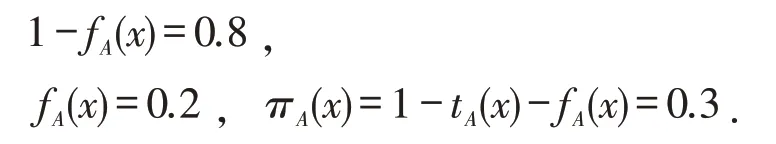
可以解释为：元素x属于A的程度是0.5，不属于A的程度是0.2，对A的未知程度是0.3.

设A为一个Vague集，当U离散时，将其表示当U连续时，将其表示为

下面给出U为有限离散集时的几个定义。

定义2.3 设论域U={x1,x2,…,xn} （即为离散有限集），A,B是U上的两个Vague 集，其中

定义Vague集的被包含、包含、相等运算如下：

A ⊆B 当且仅当∀xi∈U,tA(xi)≤tB(xi)

且1-fA(xi)≤1-fB(xi)，即fA(xi)≥fB(xi)

A=B当且仅当∀xi∈U,tA(xi)=tB(xi)

且fA(xi)=fB(xi).

定义2.4 设U={x1,x2,…,xn}为论域，A是U上的Vague集，如果集合

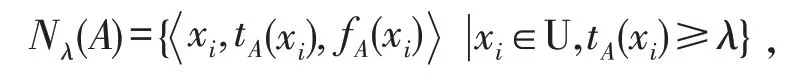
其中λ∈[0,1]

则称Nλ(A) 为A的真隶属度的λ水平集.称（其中，tA(xi)≥λ，l为tA(xi)≥λ的xi元素的个数）为真隶属度λ水平的均值，记为

定义2.5 设论域U={x1,x2,…,xn}，A,B是U上的两个Vague集，其中

B=对于λ∈[0,1]，如果则称Vague 集A,B为基于真隶属度λ水平的均值的相等，记为定理2.1 若（证明略）

三、Vague集间模糊距离的定义

定义3.1 设U={x1,x2,…,xn}为论域，V(U)表示U上的全体Vague 集，是V(U)×V(U)→[0,+∞)的映射，如果对任意A,B,C ∈V(U)，下列（1）～（3）成立

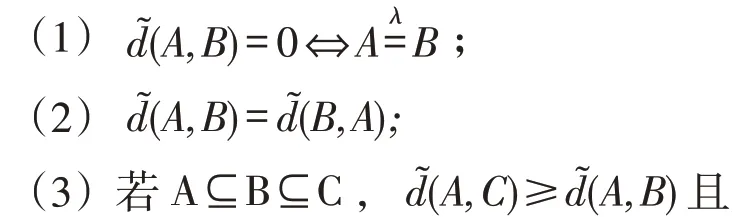
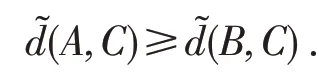
则称是V(U) 上的模糊距离，表示A,B之间的模糊距离.

给出的Vague集间的模糊距离的几种具体公式为：

定理3.1 设U={x1,x2,…,xn}为论域，

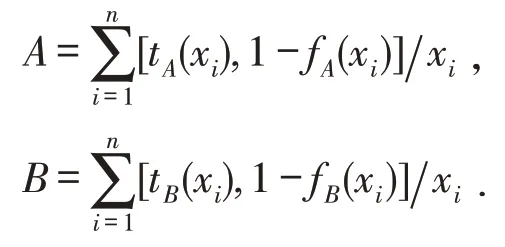
对于λ∈[0,1]，Nλ(A)≠Φ，Nλ(B)≠Φ，

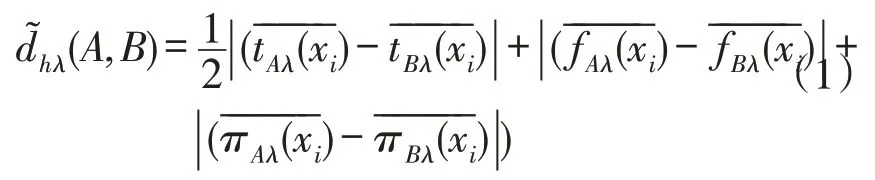
则(A,B)是Vague 集A,B之间的模糊距离，并称为Vague 集A,B之间λ水平模糊Hamming 距离.称为Vague集A,B之间的模糊Hamming距离集．

证明 显然(A,B)≥0．

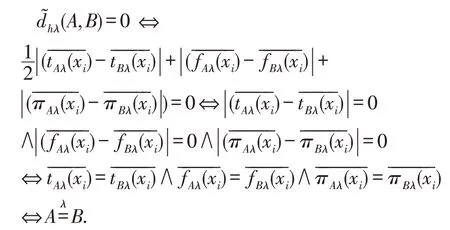
显然(A,B)(B,A)．

⇒(A,C)≥(A,B)．同理可证

(A,C)≥(B,C)．

定理3.2 设U={x1,x2,…,xn}为论域，

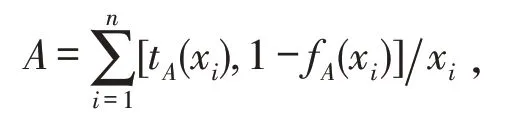
B=对于λ∈[0,1]，

Nλ(A)≠Φ，Nλ(B)≠Φ，令

则(A,B)是Vague 集A,B之间的模糊距离，称为Vague 集A,B之间λ水平模糊Euclidean 距离。称为Vague 集A,B之间的模糊Euclidean距离集。

定理3.3 设U={x1,x2,…,xn}为论域，

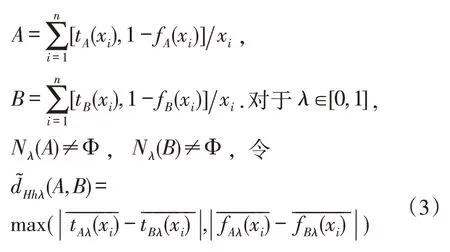
定理3.2、3.3易证，这里从略。并且显然有如下结论。

四、示例与讨论

1.示例

设U={x1,x2,x3,x4}为论域，A,B为上的Vague集，其Vague 值[t(x),1-f(x)]如表1 所示。由公式（1）、（2）、（3）计算距离，结果见表2。

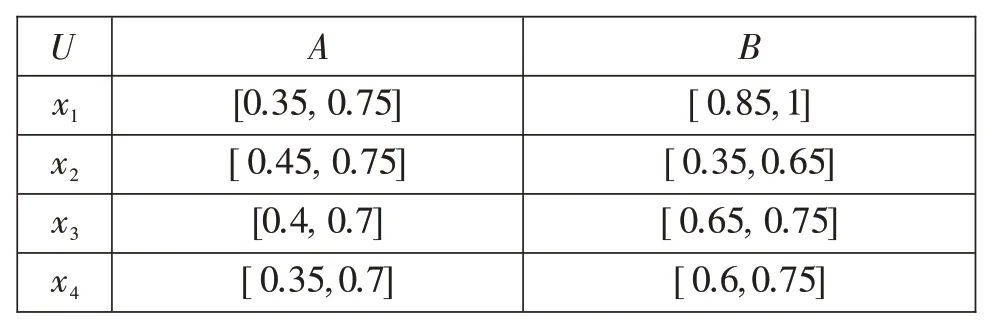
表1 Vague集A,B Vague值[t(x),1-f(x)]表

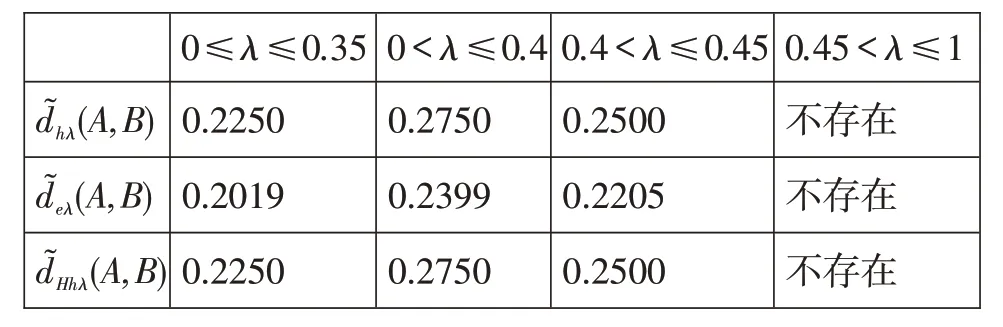
表2 Vague 集A,B 间的各种距离计算结果表

2.选取λ值的讨论

直观的看，Vague 集是一个依隶属度(真隶属度、假隶属度与犹豫度)不同的“朦胧集”，真隶属度越高、假隶属度与犹豫度越低，其对应元素越属于该集合，反之越不属于该集合。因此，用一个确定数表示集合的距离不如用模糊数表示更为合理。本文提出的Vague 集间的距离是一个依据λ值的距离，当选定λ值，就是忽略了真隶属度小于λ的元素，突出考虑真隶属度大于λ的元素的距离，这样突出了“主要矛盾”。

定义4.1 设U={x1,x2,…,xn}为论域，

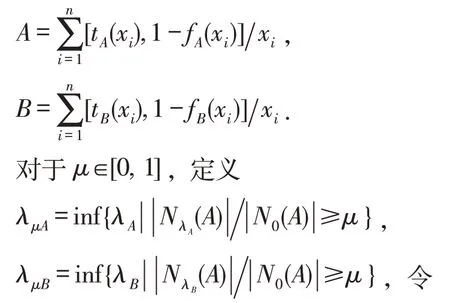
λμ=min{λμA,λμB}，则称λμ为Vague 集水平集浓度不低于μ的截集水平.（注：表示集合·的势）.

显然，上述定义可以推广到有限个Vague集的情形。

如果给出了Vague集A,B真隶属度tA(xi),tB(xi)的分布函数，还可以根据分布函数确定截集水平λμ。

由上节距离的定义发现,λ的取值比较重要,λ取不同的值直接影响距离的值。

（1）当λ=0，则考虑的是全体元素的在内Vague集间的距离；

（2）当λ≠0，则考虑的是真隶属度t(xi)≥λ元素的Vague集间的距离；

（3）在实际应用中，应根据问题的需要确定截集水平λμ，但一般不选太低的μ值，如可选μ≥0.5 等等，甚至取μ=1。

五、结语

本文对Vague集间以真隶属度的λ水平集为基础定义了其三种新模糊距离，体现了以真隶属度为标准的突出“主要元素”的思想，丰富了Vague集间距离公式。还需指出，同时考虑真隶属度与假隶属度水平集基础上的模糊距离的定义是值得研究的课题。