基于稀疏和近邻保持的极限学习机降维
2019-04-12陈晓云廖梦真
陈晓云 廖梦真
随着大数据时代的到来,人们对数据的处理正面临巨大挑战.在大数据应用研究中,高维数据分析与研究是其主要内容之一.在现代机器学习与统计学的研究背景下,高维数据所引发的维数灾难主要表现为:众多低维空间中表现良好的算法在面对高维数据时性能急剧下降.其主要原因有:1)维数增加导致数据空间体积急剧膨胀、同等数量样本分布非常稀疏,难以形成有效的簇;2)高维空间中存在测度“集中现象”,使样本点间距离度量的类区分性随着维数增加而减弱;3)样本数据包含大量冗余信息对聚类或分类无用,甚至会降低算法的性能.基于上述原因,对降维方法进行研究是十分有必要的.
总体上说,面向聚类的降维方法均为无监督降维方法,可分为线性降维和非线性降维.当前,多数无监督线性降维方法假设观测数据落在一个低维流形子空间中,通过寻找高维空间到低维子空间的线性投影实降维,如主成分分析(Principal component analysis,PCA)[1]、局部保持投影 (Locality preserving projections,LPP)[2]、近邻保持嵌入(Neighborhood preserving embedding,NPE)[3]和稀疏保持投影(Sparsity preserving projections,SPP)[4].PCA是最经典的线性降维方法,以最大化投影散度为目标,但未考虑样本间的近邻结构关系,不适合分布于流形上的非线性数据;LPP和NPE则考虑了样本间的近邻结构,LPP以保持降维前后样本间的近邻关系不变为目标,而NPE旨在保持降维前后样本间的局部近邻结构;SPP的优化目标是使降维前后样本间的稀疏表示结构得以保持.但当数据非线性分布时,上述线性降维算法就会失效.为弥补线性降维算法的不足,各种非线性扩展方法被提出,如核主成分分析(Kernel principal component analysis,KPCA)[5]和局部线性嵌入(Locally linear embedding,LLE)[6].KPCA是PCA基于核技巧的非线性推广,用于对非线性分布数据降维;LLE以保持投影前后局部线性关系不变为目的构造目标函数.然而这些非线性降维方法无法求出显式的映射函数,当有新样本加入时,需要重新学习优化模型.
极限学习机(Extremelearningmachine,ELM)[7−8]最早被用于训练单隐层前馈神经网络,具有学习速度快、泛化能力强等特点,为有监督学习如分类和回归提供了简单有效的方法[9−10].2014年,Huang等基于流形正则的思想将ELM推广到无监督学习任务,提出了一种新的非线性降维方法无监督极限学习机(Unsupervised extreme learning machine,US-ELM)[11].该方法很好地利用了ELM的逼近能力,通过非线性映射将原数据投影到低维空间中,并能够得到显式的非线性映射函数.但该方法利用高斯函数描述近邻样本间的相似度,由于高斯函数用到距离测度,难以避免地也存在高维空间中测度“集中现象”,即样本点间高斯相似性度量的类区分性随着维数增加而减弱,进而影响降维算法性能.此外,US-ELM 直接利用给定高斯函数计算样本近邻表示系数,不具有数据自适应性.
针对上述问题,本文对US-ELM进行改进,同时考虑非线性数据的局部线性表示和全局稀疏表示.其中,局部线性表示用于解决非线性流形数据的刻画问题,以获取数据的局部结构[12];全局稀疏表示用于描述数据的全局结构[13];并通过加权参数融合近邻线性表示信息和稀疏表示信息.由此,我们提出基于稀疏和近邻保持的极限学习机降维方法(SNP-ELM),使得降维前后样本间的局部近邻表示关系和全局稀疏性保持不变.SNP-ELM通过学习得到近邻表示系数,较之US-ELM具有更好的数据自适应性.
1 极限学习机
极限学习机本质上是一种单隐含层前馈神经网络,其结构如图1所示[14].ELM 网络的训练主要分为两个阶段.第一个阶段是ELM网络结构构建,隐含层将输入数据映射到n维的特征空间中,nh为隐节点个数.定义隐含层关于xi的输出向量为h(x)=[h1(x),h2(x),···,hnh(x)]∈R1×nh。其中,x∈Rm,hi(x)是第i个隐节点的输出,其输出函数可以表示为:
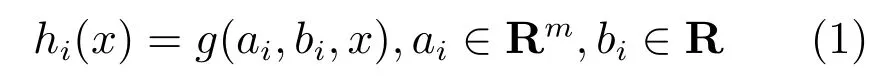
其中,g(ai,bi,x)为非线性激励函数,常用的函数有Sigmoid函数和Gaussian函数.本文采用Sigmoid函数,其表达式为:
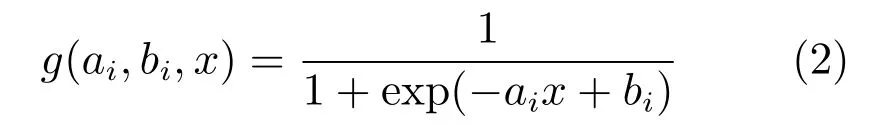
式中,ai为第i个隐节点的输入权值,bi为第i个隐节点的偏差,在ELM网络中输入权向量ai和隐节点偏差bi是随机产生的.
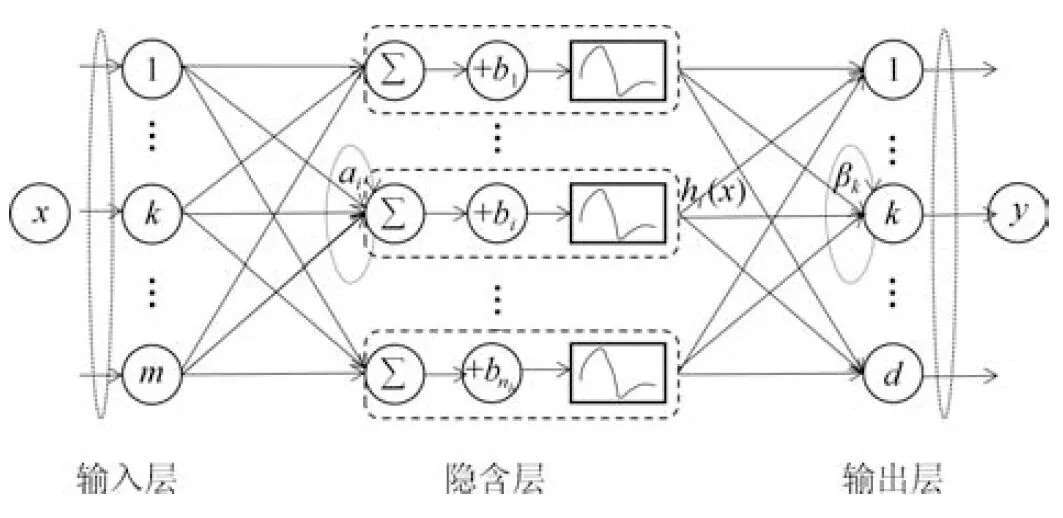
图1 ELM网络结构示意图Fig.1 ELM network structure
对于数据集X,ELM隐藏层输出为:
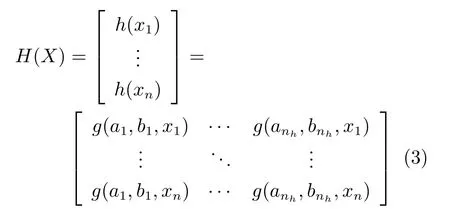
若隐藏层到输出层的权重矩阵为β=[β1,β2,···,βm],则 ELM 网络的输出为

第二阶段是基于ELM网络结构求解输出权重矩阵β,通常根据ELM网络学习任务的不同构建不同的模型来求解输出权重矩阵β.经典的ELM模型用于解决有监督学习问题,如:分类和回归.对于含n个样本的训练集S={(xi,yi)|xi∈X⊆Rm,yi∈Y⊆Rd,i=1,···,n},xi为输入变量,yi为输出变量,则其模型表示:
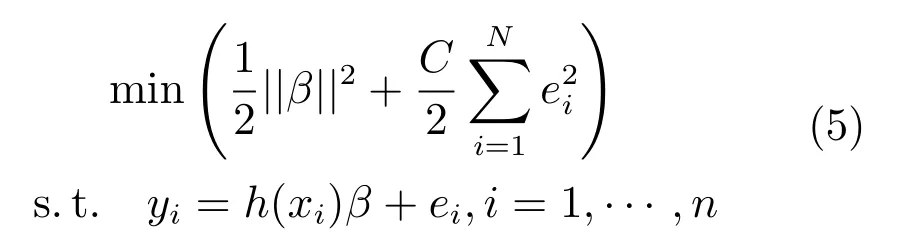
其中,目标函数的第一项为正则项,用来控制模型的复杂度;第二项为表示误差,ei∈Rd是第i个样本的误差向量,C为惩罚系数.
近年来,Huang等将ELM推广到无监督学习,提出基于流形无监督极限学习机,其模型为:
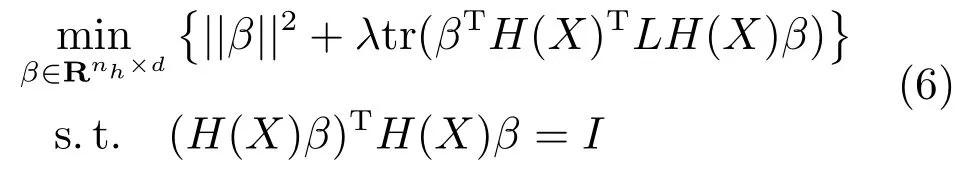
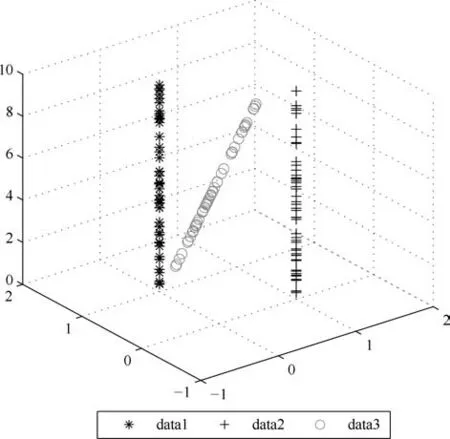
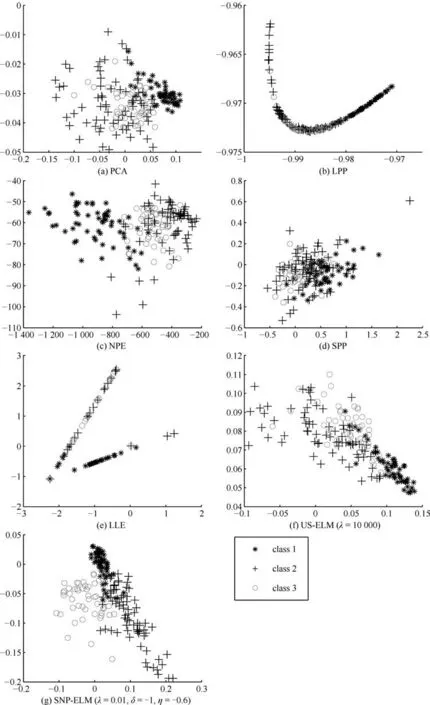
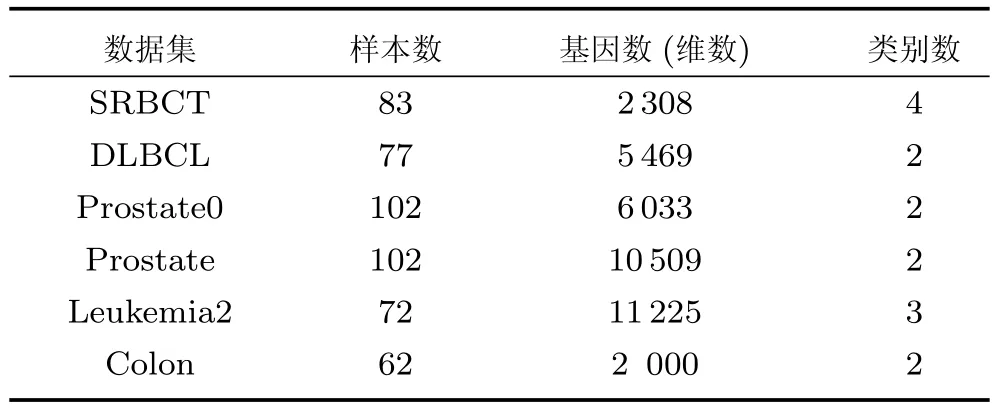
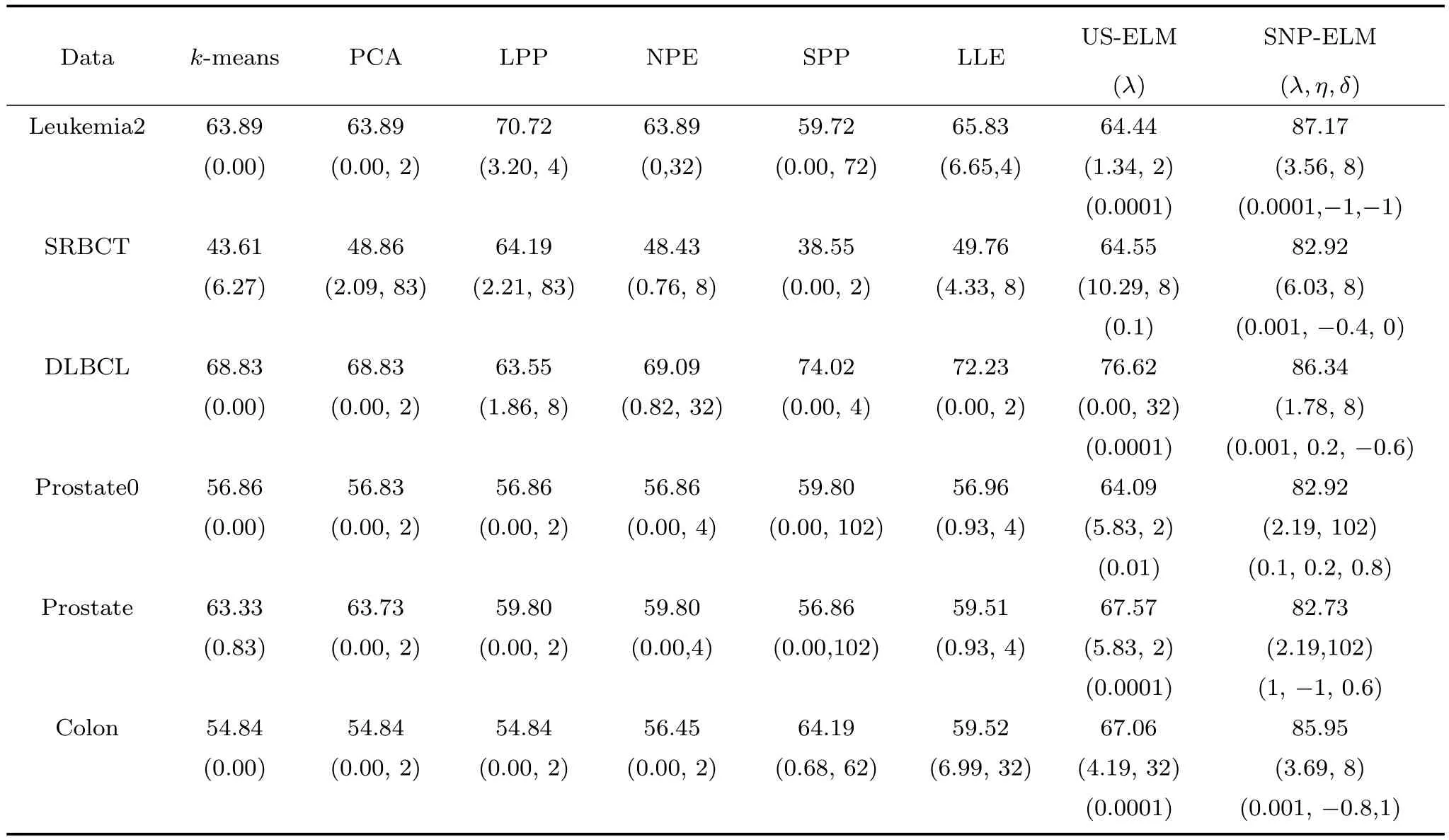
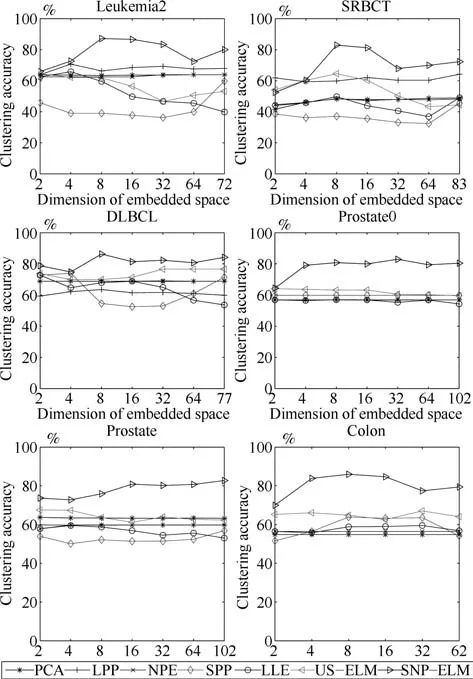
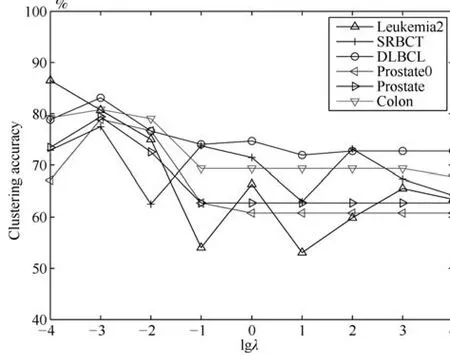
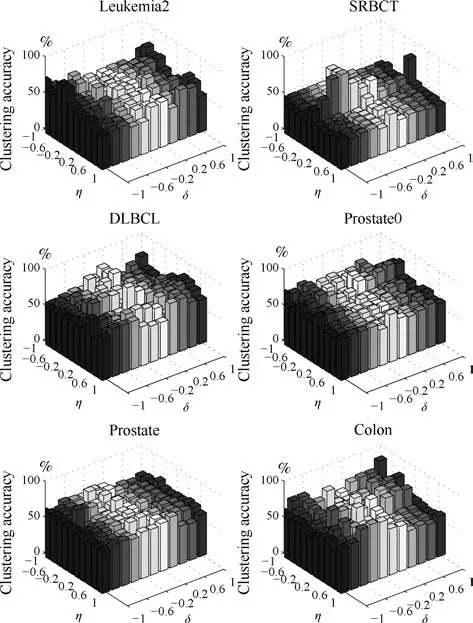
第二项为流形正则项,目的是使网络结构输出Y保持原输入数据X的流形结构不变,其中,tr(·)表示矩阵的迹,L为数据X的拉普拉斯矩阵,I为单位阵,H(X)∈Rn×nh为隐含层输出矩阵.USELM将输入数据投影到d维空间中,当d US-ELM算法引入流形正则化的思想,使得原始数据的流形结构经过US-ELM投影后得以保持,即若在原空间近邻的两个样本在投影空间中仍然保持近邻[2].US-ELM算法的流形结构直接用Gaussian距离刻画,随着数据维数的增加,该距离度量的类分类性会随之减弱.针对这一问题,本文采用近邻表示来自适应地获取数据的低流形结构,同时用稀疏表示来挖掘数据的全局结构.在此基础上提出SNP-ELM 算法,使得数据在新的投影空间中保持其在原空间的近邻和稀疏表示结构. 近邻表示[4]:在样本集X=[x1,x2,···,xn]∈Rm×n中用xi的k近邻进行线性表示xi,其表达式为: 其中,Nk(xi)表示xi的k近邻,wij为近邻表示系数,当xi∈Nk(xi)时,wij=0. 稀疏表示[5]:样本xi可大致由该样本集中的少量样本线性表示.而当xi由整个样本空间X进行线性表示时,其表示系数是稀疏的.其数学模型表示为: 其中,si∈Rn为稀疏表示系数,||s||0是s非零元素个数.由于l0范数非凸且NP难,因此用凸的l1范数代替.同时为了确保稀疏表示的平移不变性,我们引入表示系数和为1的约束,则式(8)变为: 其中,I1为所有元素均为1的n维向量.式(9)是凸的,可以利用线性规划方法求解,如基追踪算法(Basis pursuit,BP)[15]. SNP-ELM模型为: 第二项的目的是使得投影后的数据保持原数据的近邻和稀疏表示结构,其中W=[w1,w2,···,wn]为近邻表示系数矩阵,wi表示xi的近邻表示系数,可以用模型(7)求解:S=[s1,s2,···,sn]为稀疏表示系数矩阵,si表示xi的稀疏表示系数,可以用模型(9)求解.δ∈R和η∈R是权重系数,分别反映W和S的重要性.映射函数为y=f(x)=(h(x)β)T. 令Z=δW+ηS,则式(10)可写成: 通过简单的代数运算,可以得到: 令ei为n维单位向量,则式(12)等价于: 式(11)可变形为: 为避免平凡解,在此引入约束(H(X)β)TH(X)β=I,则模型变为: 为求解模型(15),利用拉格朗日乘子法,得到以下拉格朗日函数: 求解广义特征值问题(17)得到最小的d个特征值及对应的特征向量构成最优的输出权重矩阵β∗. 当nh>n时,HT(X)H(X)的维数比较高,直接求解式(17)广义特征值问题,需要消耗较大的内存.为解决这个问题,令β=HT(X)α,式(17)两边同时左乘(H(X)HT(X))−1H(X).得到: 易知模型(17)与模型(18)具有相同特征值.特征向量具有以下关系 因此解得广义特征值问题(18)的最小的d个特征值及对应的特征向量构成矩阵α∗.进而可获得模型(17)的解矩阵β∗=HT(X)α∗. 基于上述分析,基于稀疏和近邻保持的极限学习机降维算法归纳如下: 算法1.SNP-ELM算法 输入:数据矩阵X,参数λ,δ,η. 输出:降维后样本矩阵Y. 1)计算k近邻图. 2)通过式(8)计算近邻重构矩阵W. 3)通过式(10)计算稀疏重构矩阵S,计算Z=δW+ηS,A=I−Z−ZT+ZTZ. 4)初始化ELM 网络,nh为隐藏层节点个数,随机初始化输入权重a∈Rn×nh,偏置b∈Rnh根据式(3)计算隐藏层输出矩阵H(X)∈Rn×nh. 5)当n>nh时,利用式(17)计算得到输出权重矩阵β;否则,利用式(18)计算得到α,再计算输出权重矩阵β=HT(X)α. 6)计算降维后样本矩阵Y=H(X)β SNP-ELM算法中计算k近邻图的时间复杂度是O(mnlogn);计算近邻重构矩阵W是求解了n次式(8),其时间复杂度为O(nk3);用BP算法求解式(10)的时间复杂度为O(n3),因此计算稀疏重构矩阵S的时间复杂度为O(n4);计算广义特征值式(18)的时间复杂度为O(n3h),求解广义特征值式(20)的时间复杂度为O(n3).因此SNP-ELM算法的时间复杂度为O(mnlogn+n4+nk3). 本文提出的SNP-ELM降维算法有两个重要目的,其一是便于高维数据的可视化分析,其二是面向聚类分析的降维可有效地提高聚类准确性,故进行数据可视化及高维基因数据降维聚类实验,两个实验的实验环境均为Win7系统,内存4GB,所有方法均用Matlab2012b编程实现.两个实验均采用相同的参数设置,LPP、NPE、US-ELM和SNP-ELM的近邻数k均设为5;US-ELM和SNP-ELM的隐藏层节点个数均设为1000;US-ELM的参数λ及SNP-ELM 的参数λ统一取{10−4,10−3,···,104},SNP-ELM 的参数δ和η的搜索范围为[−1,1],变化步长为0.2. 本文实验所对比的降维方法主要有以下几种:1)线性降维方法:PCA、LPP、NPE和SPP;2)非线性降维方法:LLE和US-ELM.其中LPP、NPE、LEE和US-ELM都使得降维后的数据保持原数据的近邻结构,SPP保持数据的稀疏表示结构,PCA的目标是使得降维后数据方差最大. 本实验中,我们分别用PCA、LPP、NPE、SPP、LEE、US-ELM和SNP-ELM 7种方法将一个人造数据和一个真实的UCI数据Wine分别投影到一维和二维空间,直观地展示SNP-ELM算法的性能,并选取每个降维方法的最优结果进展示. 1)一维可视化 本实验使用的三维人造数据如图2所示,该数据包含3类,每类有50个样本,该实验分别将数据降到一维,实验结果如图3所示. 图2 人造数据集Fig.2 The toy dataset 图3 人造数据一维可视化结果Fig.3 The 1D visualization results of toy dataset 从图3可以看出PCA以投影后的样本方差最大为目标,其降维结果近似于把该数据投影到Z轴方向,但其将该数据投影到一维时三类数据的可分性较差.LPP、NPE、LLE和US-ELM 均以降维后样本保持原样本的近邻结构为目的,因此其降维效果略有改善.其中LLE和US-ELM是非线性降维方法,其降维后不同类样本的分离程度较LPP和NPE高些.稀疏保持投影方法SPP以降维后样本保持原样本的稀疏结构为目的,该方法将数据投影到一维后不同类样本的分离程度与US-ELM相当.SNP-ELM 是一种非线性降维方法,它使降维后样本同时保持数据的近邻结构和稀疏结构不变.SNP-ELM虽然无法使得该数据投影到一维后三类样本完全分离,但其降维后不同类样本可分性是7种降维方法中最优的,只有少数第三类样本与第二类样本相互重叠. 2)二维可视化 本实验使用UCI数据集Wine数据,Wine数据包含来自3个类的178个样本,每个样本有14个特征.实验结果如图4所示. 由图4可以看出,经7种降维方法将Wine数据投影到2维时仍无法完全分离3类样本.但从不同类样本的重叠程度上可以看出,SPP将数据降到二维后3类数据完全重叠在一起,降维效果最差.用PCA、LPP、NPE、LLE和US-ELM 这5种方法降维后第一类数据能较好地分离,而第二类和第三类数据完全重叠在一起.本文方法将Wine数据降到二维后,不同类数据的重叠程度最低,不同类样本的可分性最好. 本实验采用高维基因表达数据测试本文方法与对比方法面向聚类任务时的降维效果.为了观察本文降维方法将数据投影到不同维数,特别是投影到较低维时基因表达数据聚类效果,将数据分别投影到21,22,23,24,···,2n维.该实验以降维后样本的k-means聚类准确率衡量降维质量,实验中的聚类准确类采用文献[13]的计算方法.计算公式如下: 其中,n为样本数,δ(x,y)表示当x=y时,δ=1,否则δ=0;si和ri分别为样本原始类标签和经聚类算法聚类后得到的类标签:map(ri)将聚类得到的类标签映射成与样本数据自带的类标签等价的类标签. 1)实验数据集 实验所选用的6个公开的基因数据集:SBCRT、DLBCL、Leukemia2、Prostate[16]、Prostate0和Colon[17],这些数据的详细描述见表1. 2)聚类准确率比较 图4 Wine数据二维可视化结果Fig.4 The 2D visualization results of Wine 表1 基因表达数据集描述Table 1 Summary of gene expression data sets 为减少k-means初始中心随机选取以及USELM和SNP-ELM 方法随机权重产生的随机误差.为便于比较,减少实验结果随机性的影响,实验中US-ELM和SNP-ELM分别运行10次,再将每次降维后数据集执行10次k-means聚类,取100次聚类准确率的平均值作为各自方法的最终准确率,而其他降维方法的聚类准确率是10次k-means聚类准确率的平均值.最终实验结果如表2所示,表中给出聚类准确率的均值 (方差、维数),其中维数为每个数据最优聚类结果所对应的维数.对两种极限学习机降维方法US-ELM 和SNP-ELM 分别给出最优聚类结果所对应的参数.LPP、NPE、LLE、US-ELM 和SNP-ELM 这5种方法都在降维时保持了原始数据的近邻结构,SPP和SNP-ELM都保持了原始数据的稀疏结构,其中LLE、US-ELM 和SNP-ELM 是非线性降维方法,SNP-ELM同时保持原始数据的近邻结构和稀疏结构.将这5种方法降维后的聚类准确率进行对比可以发现:1)将NPE和LPP分别与LLE和USELM的准确率进行对比,可以发现后者的准确率比前者高,这是因为LEE和US-ELM分别是NPE和LPP的非线性推广,非线性降维方法更适用于非线性分布的基因表达数据.2)SPP与LPP、NPE进行比较其聚类结果各有千秋,在DLBCL、Prostate0和Colon这3个数据集上SPP的结果较好,而在其他数据集上LPP和NPE的结果较好,这说明稀疏保持和近邻保持各有优势.3)SNP-ELM的聚类准确率是最高的,其主要原因是SNP-ELM既是非线性降维方法,又同时保持了原始数据的近邻表示结构和稀疏表示结构使得降维后低维空间的数据保持了更多的判别信息.将表2中的所有方法进行对比,可以发现基于ELM的2种降维方法的准确率普遍优于其他降维方法.特别是SNP-ELM算法考虑到降维后样本局部近邻关系和全局稀疏性保持不变,从而使其在全部6个基因数据降维后的聚类准确率最高,且高于其他方法及US-ELM方法10%以上.这说明SNP-ELM是一种有效的高维非线性降维方法. 为进一步对比几种降维方法在不同维数下的聚类准确率,分别选取目标维数2,4,8,16,32,···执行各种降维算法,各种降维算法在不同维数下的聚类准确率如图5所示.从图5可以看出SNPELM及其余6种降维算法将6个数据集投影到相同维数的特征空间时,SNP-ELM的聚类准确率都是最高的.而对于SNP-ELM算法,除Prostate和Prostate0两个数据集,在其他4个基因数据集上都在8维处得到最高的聚类准确率. 表2 基因数据集上聚类准确率(%)Table 2 Clustering accuracy comparison(variance)on gene expression data sets(%) 图5 将6个数据集映射到不同维度特征空间时的聚类准确率Fig.5 Clustering accuracy on six gene expression data in different dimensions 3)参数分析 SNP-ELM 模型有3个参数λ,δ和η,其中λ为正则参数.δ和η为权重系数,分别表示近邻重构系数和稀疏重构系数的重要性.本节讨论不同参数对实验结果的影响,由前面的实验结果可知将基因表达数据降到8维时能够得到较高的聚类准确率,因此在进行参数分析时我们固定维数为8.根据3个参数在SNP-ELM 中的不同作用,将其分为两组分别进行分析,正则参数λ单独分析,权重系数δ和η一起分析.其中,λ的取值范围为{10−4,10−3,···,104},δ和η的取值范围为[−1,1],取值步长为0.2. 图6给出δ=η=−0.2时,SNP-ELM降维的聚类准确率随参数λ不同取值的变化情况.从图6可以看出,除了Leukema2在λ=10−4时聚类准确率达到最高,其余5个基因表达数据均在λ=10−3时聚类准确率达到最高.这说明对高维基因数据而言,λ取较小值时本文方法能达到较好效果. 图6 聚类准确率随参数λ的变化情况(δ=η=−0.2)Fig.6 Variation of accuracy with respect of parametersλ(δ= η= −0.2)) 图7给出λ=0.001时,不同δ和η取值下的聚类准确率.从图7可以看出当δ取值自[−0.6,−0.2],η取值自[−0.2,0.2]时,对高维基因表达数据而言SNP-ELM算法可以取得较高的聚类准确率. 图7 不同δ和η取值下的聚类准确率(λ=0.001)Fig.7 ariation of accuracy with respect of parametersδandη(λ=0.001) 目前,ELM模型主要用于有监督分类或回归问题,本文则对ELM模型推广到无监督降维问题进行了进一步研究,提出基于稀疏和近邻结构保持的极限学习机降维算法SNP-ELM.SNP-ELM通过模型优化求解计算近邻表示系数,具有一定的数据自适应性,实验结果表明SNP-ELM算法在Wine数据和基因表达数据集上性能优于其他对比方法.从研究中我们可以得到以下2个结论:1)对Wine数据、高维基因表示数据降维时,同时考虑稀疏结构和近邻结构比只考虑单一结构更有效;2)基于ELM的非线性降维方法在Wine数据和基因表达数据上优于线性降维方法.2 基于稀疏和近邻保持的极限学习机降维
2.1 近邻表示和稀疏表示
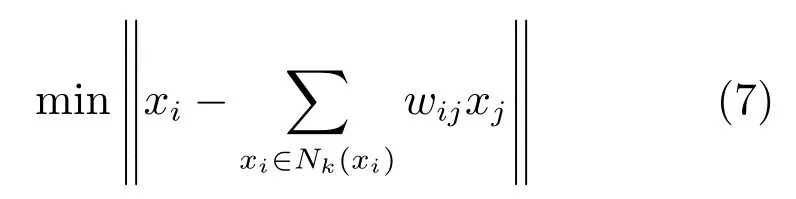
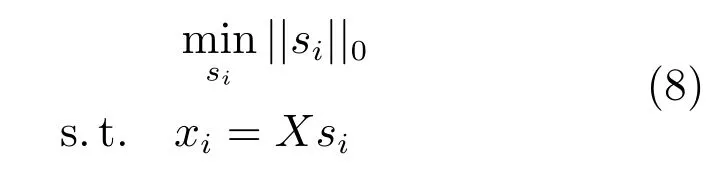
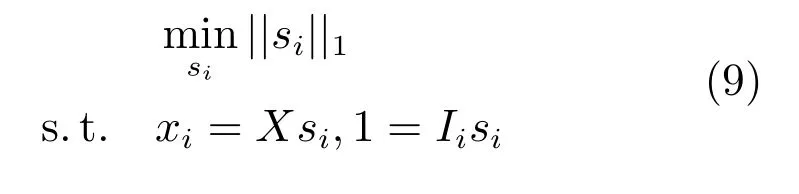
2.2 基于稀疏和近邻保持的极限学习机降维算法
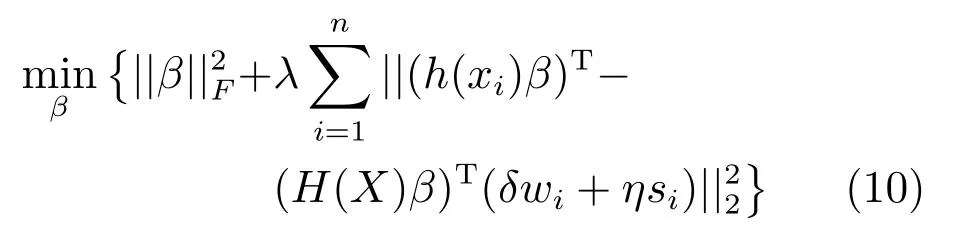
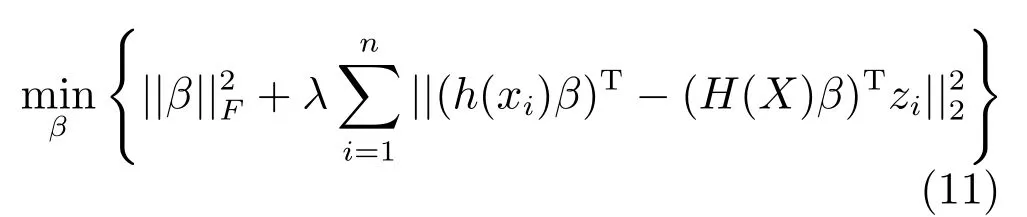
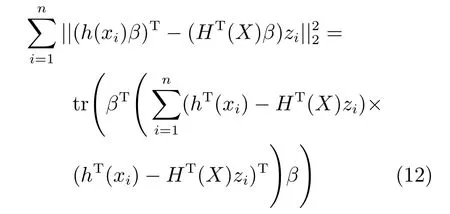
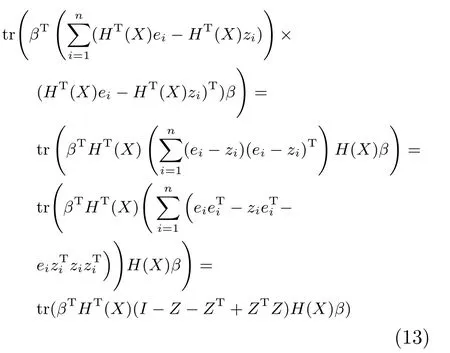
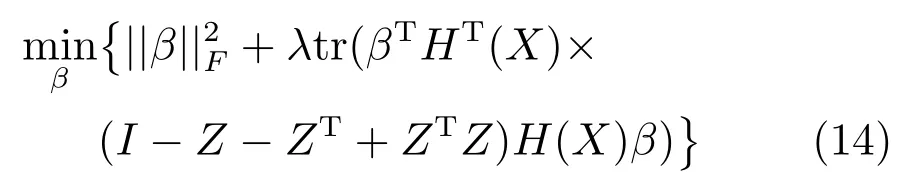
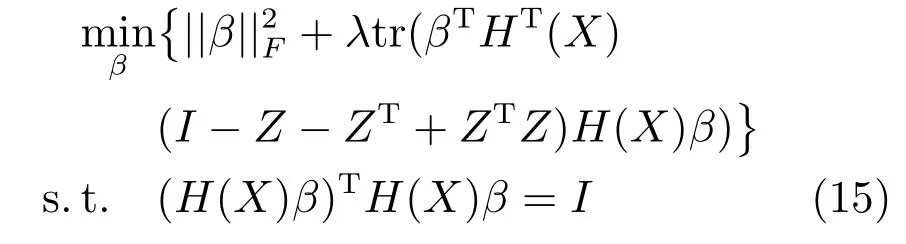
2.3 模型求解
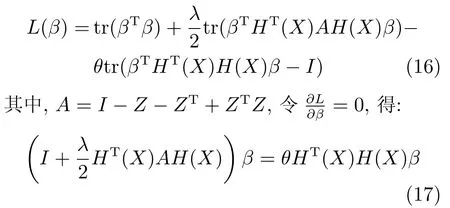
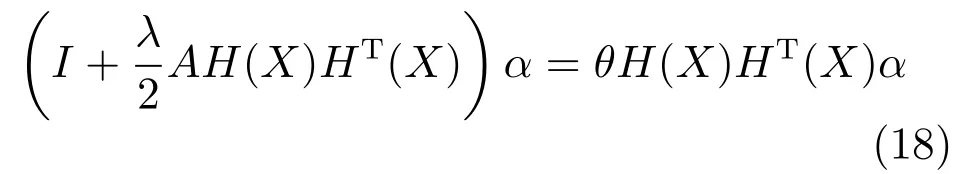
2.4 算法分析
3 实验
3.1 数据可视化实验

3.2 基因表达数据实验
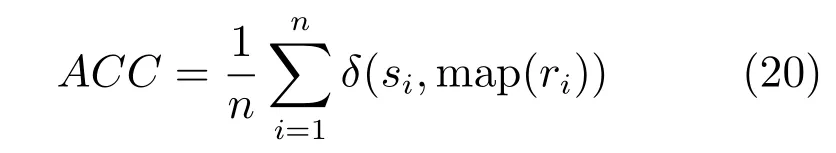
4 结论
