基于边缘增强与光谱特性保持的Pan-sharpening融合模型
2019-04-12陈超迁孟勇杨平吕罗其祥周则明
陈超迁 孟勇 杨平吕 罗其祥 周则明
在遥感应用领域,不同传感器采集的数据在空间和光谱分辨率等方面存在着较大的差异.如高分辨率对地观测卫星QuickBird、IKONOS及GeoEye-1提供了4个多光谱(Multispectral,MS)波段和1个全色(Panchromatic,Pan)波段,其中MS图像光谱信息丰富,空间分辨率较低,而Pan图像空间细节表现力好,光谱信息却比较单一.为提高MS图像的空间分辨率,常采用全色锐化(Pansharpening)方法将Pan波段图像中的空间细节注入到MS波段图像[1].如果在各个MS波段中注入同样的空间细节,融合图像将不可避免地产生光谱失真现象.为更有效地保持融合图像的光谱特性,需要对空间细节的注入方式进行进一步的研究.
现有的Pan-sharpening方法主要分为4类[2]:分量替换法(Component substitution,CS)、多分辨率分析法(Multi-resolution analysis,MRA)、基于稀疏表示的图像融合方法和基于变分PDE的图像融合方法.分量替换法由图像增强算法发展而来,代表性算法有亮度–色调–饱和度变换法(Intensity-Hue-Saturation,IHS)[3−4]与主成分分析法(Principal component analysis,PCA)[5−6].Leung 等[7]在传统IHS算法的基础上提出了一种自适应的Adaptive IHS融合算法,通过定义权重矩阵控制注入MS图像的空间细节,有效降低了融合图像的光谱失真程度.Shah等[8]提出了改进的PCA融合算法,根据交叉相关性自适应地选择需要替换的主分量,融合性能优于传统的PCA方法.考虑到传感器的调制传输函数(Modulation transfer function,MTF)在遥感图像成像过程中的重要性,Vivone等[9]在MTF-CON模型中基于MTF构造高通滤波器提取Pan图像中的空间信息,然后通过Brovy变换将其注入MS图像中,MS图像的光谱信息得到有效保持.多分辨率分析法针对遥感图像在多个分辨率下的不同特征构建相应的融合规则,有效利用了图像中的低频信息与高频信息,主要分为基于拉普拉斯金字塔的融合[10−11]与基于小波变换的融合[12−13]两类.苗启广等[14]对传统的拉普拉斯融合算法进行了改进,在图像重构过程中采用了新的算法,有效抑制了图像噪声.Otazu等[15]提出了AWLP(Additive wavelet luminance proportional)融合算法,基于多孔小波从Pan波段图像中获取小波面即高频信息,再根据MS各波段图像所占的亮度比例注入空间细节,在2006年的融合算法竞赛中展现出了良好的性能.基于稀疏表示的图像融合为了使融合图像最大程度得保持MS图像的光谱信息和Pan图像的空间信息,融合需要寻找图像的最优表示字典[16−18],Li等[19]从压缩感知理论出发,将图像融合转化为稀疏信号的恢复问题,通过BP(Basis pursuit)算法求解稀疏系数并进而重构融合图像.Jiang等[20]在此基础上构建了低分辨率MS图像与高分辨率Pan图像混合字典,降低了计算的复杂度.Li等[21]提出了一种新的稀疏表示策略,该模型能够在不需要训练集的情况下构建高分辨率MS图像字典,提高了模型的实用性.为获取高质量的融合目标,Zhu等[22]提出的SparseFI融合算法基于源图像中的Pan图像与其对应的下采样图像组成联合字典,生成的融合图像较为清晰,且光谱失真较小.近年来,变分方法应用于图像融合,取得了显著的成果,Socolinsky等[23]提出了多通道图像对比度模型,通过能量泛函最小化获取增强后的融合图像.马宁等[24]在对比度模型的基础上构造了一个改进的能量泛函,生成的融合图像具有更高的对比度.周雨薇等[25]提出了一种基于MTF的变分融合模型(MTF-Variational),根据MTF构建MS波段图像的低通滤波器以保持光谱信息,基于Laplacian高通滤波器抽取Pan图像中的空间细节,在提高融合图像空间质量的同时,有效地保持了MS图像的高光谱分辨率.Palsson等[26]假设Pan图像为各波段融合图像的线性组合,在变分框架中引入全变差正则化项(Total variation regularization,TVR),通过数值计算方法生成融合后的MS图像.Zhou等[27]将GIHS模型引入变分框架,通过MTF限制了各波段注入的空间信息,有效降低了融合图像的光谱失真.
融合图像常应用于目视解译和地物分类,因此,需要生成兼具高空间对比度和高光谱分辨率的融合产品.本文提出一种基于边缘增强与光谱特性保持的变分融合模型,能量泛函由4项组成.基于Pan与MS波段图像间的线性组合关系定义细节注入能量项,通过拟合退化后的Pan图像与MS图像间的线性关系得到各波段的权重系数;为提升融合图像的目视解译效果,基于梯度加权函数定义边缘增强项,有效地保持了全色波段图像中感兴趣目标的几何结构,显著提高了图像的对比度;为降低融合图像的光谱失真,基于MS波段传感器的MTF定义光谱保真能量项,根据各波段图像的特性自适应地注入空间细节;为解决Pan-sharpening模型的不适定性问题,在变分框架中引入了L1正则化项,保证了数值解的稳定性,与TV正则化相比,L1正则化的稀疏性能够更有效地保持融合图像的边缘.
1 融合模型
1.1 能量泛函
高分辨率Pan波段图像和融合后的各波段图像有如下的线性关系:
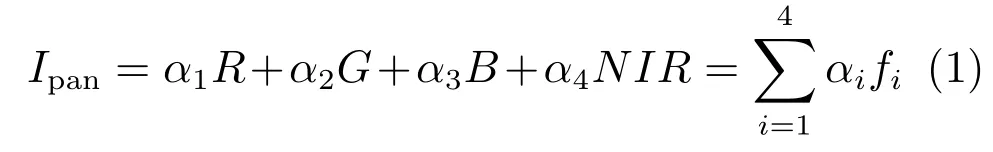
式中,R,G,B和NIR分别代表融合后的红、绿、蓝和近红外波段图像,αi为4个波段的权重系数,fi为第i波段的融合图像.假设退化到MS图像分辨率后的Pan图像与低分辨率MS各波段图像间的线性关系保持不变,权重系数αi可通过下式计算:
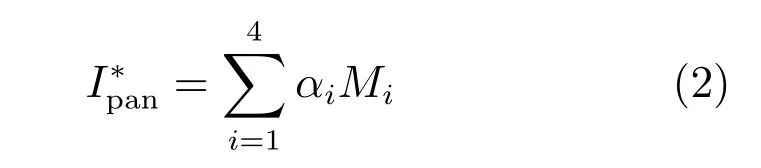
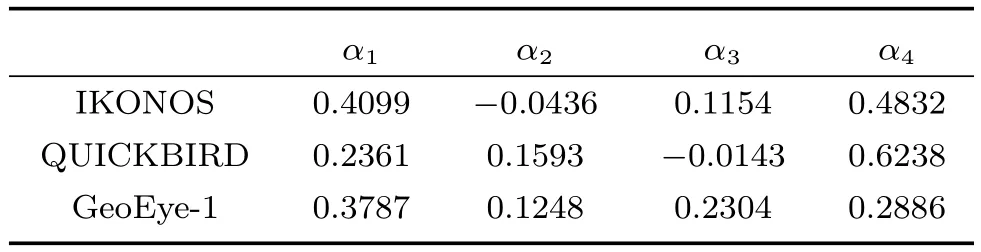
表1 IKONOS、QuickBird和GeoEye-1中的权重系数Table 1 The Weight coefficient of IKONOS,QuickBird,and GeoEye-1
细节注入项定义如下:
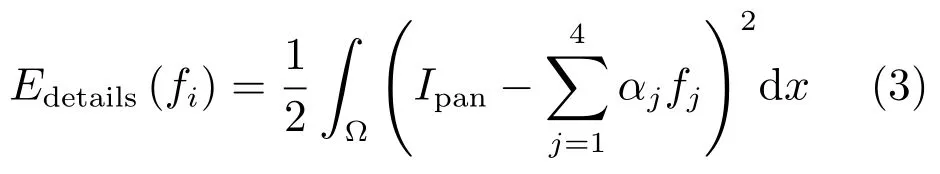
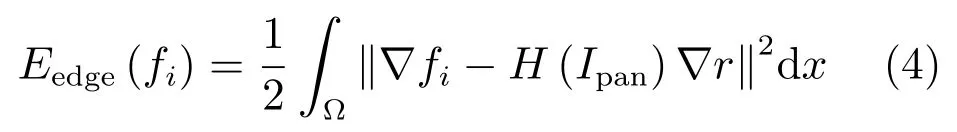
其中,∇r=∇Ipan/‖∇Ipan‖是归一化后的Pan图像梯度.加权函数H(Ipan)的定义为:H(Ipan)=exp(−c/‖∇Ipan‖),全色波段图像在强梯度边缘处,梯度幅值‖∇Ipan‖较大,由加权函数定义可知函数值接近于1,加权后的归一化梯度H(Ipan)∇r→∇r,强梯度边缘信息得到了保持.而在弱梯度边缘处,梯度幅值‖∇Ipan‖较小,相应权值趋向于0,加权归一化梯度H(Ipan)∇r→0.参数c用于调整加权函数的权重,需要根据遥感数据集的特性合理选择,对于QuickBird、IKONOS及GeoEye-1数据集,c分别取60、70和80.
图1(a)为QuickBird的Pan波段图像,图1(b)为Pan波段图像的梯度强度图,图1(c)为加权函数H处理后的梯度幅值图,经过加权处理后,图像中的强梯度边缘得到了增强,显然,该能量项能够突出图像中目标的几何结构,抑制由于噪声带来的虚假边缘.
从Pan图像抽取并注入到MS图像的高频成分提高了空间质量,但可能带来光谱特性的畸变,需要根据多光谱传感器的MTF自适应地确定注入细节的多少[25],为此,需要根据MTF设计相应的低通滤波器,使得与之互补的高通滤波器能够根据多光谱传感器的特性确定注入的空间细节的数量.Wald协议指出,融合图像退化至原分辨率后,应与融合前的MS图像十分接近,退化过程可通过多孔小波变换实现,且用于退化的滤波器应由相应波段传感器的MTF设计[28].根据Wald协议,光谱保真项定义如下:
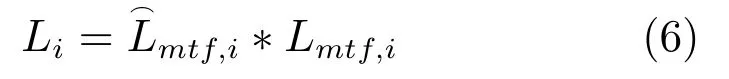
Lmtf,i基于多光谱传感器在截断Nyquist频率处的MTF设计[25],为在滤波器每两个模板值之间插入0值后的上采样版本.式(5)中的低通滤波通过多孔小波分解实现,分解层数由公式N=log2(NMS/NPan)确定,NMS、NPan分别为MS和Pan图像的空间分辨率.高分辨率卫星各波段传感器在Nyquist频率处的MTF值如表2所示[28]:

图1 梯度幅值对比图Fig.1 Comparison of gradient magnitude
为抑制图像噪声、保证数值解的稳定性,在变分框架中引入L1正则化项:
模型的能量泛函定义如下:
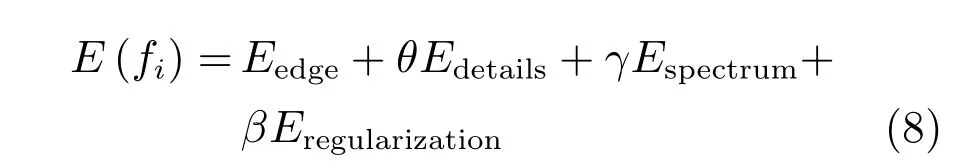
式中,θ,γ和β为各个能量项的权重系数,需要通过融合实验确定.
1.2 数值求解格式
由于能量泛函中含有非光滑的L1范数,本文采用Split Bregman迭代算法[29]求解.引入辅助变量d=∇f,将无约束优化问题转换为带约束的优化问题,即:
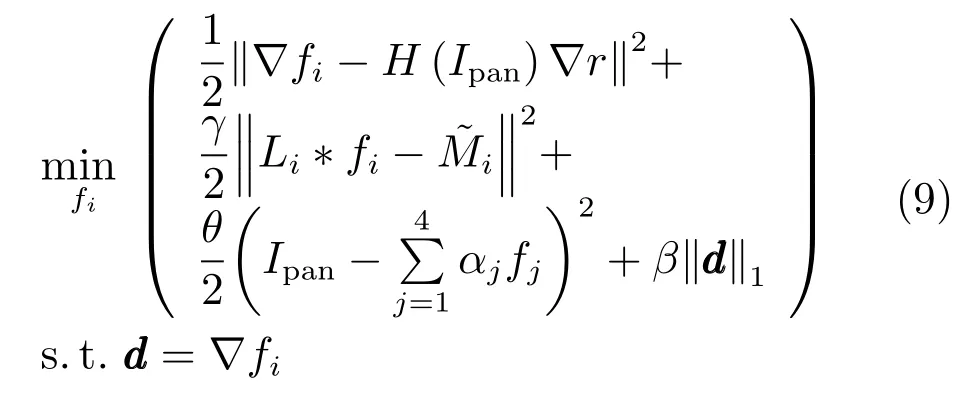
在此基础上,采用增广拉格朗日乘子,将式(9)转换为:
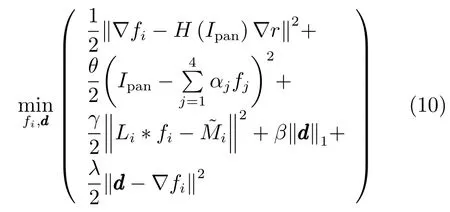
其中,惩罚项系数λ为正常数,本文取λ=0.1.引入变量bk,通过Bregman迭代,将式(10)中关于fi和d的求解问题分解为两个优化子问题,即:
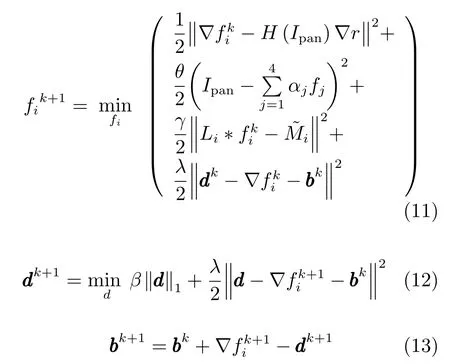
式(11)为可微分最优化问题,其Euler-Lagrange方程为:
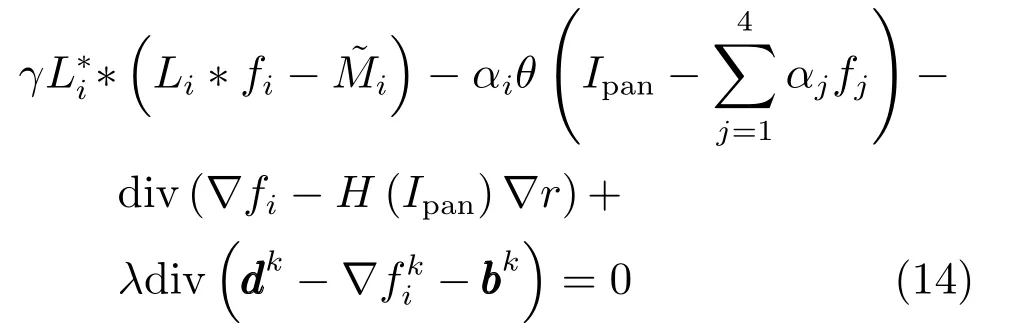
其中,L∗为L的共轭转置矩阵,差分格式定义如下:
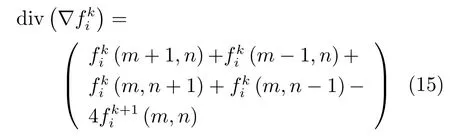
通过Gauss-Seidel迭代对式(14)求解,可得:
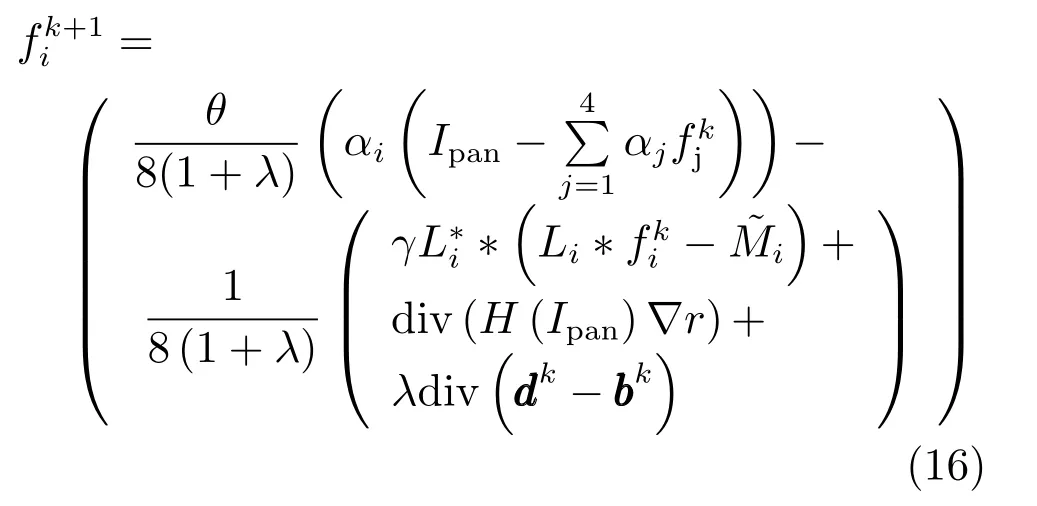
由于式(12)是严格凸的并且含有不可微项‖ d‖1,计算广义导数并导出其对应的Euler-Lagrange方程,引入Shrinkage算子得到其解为:
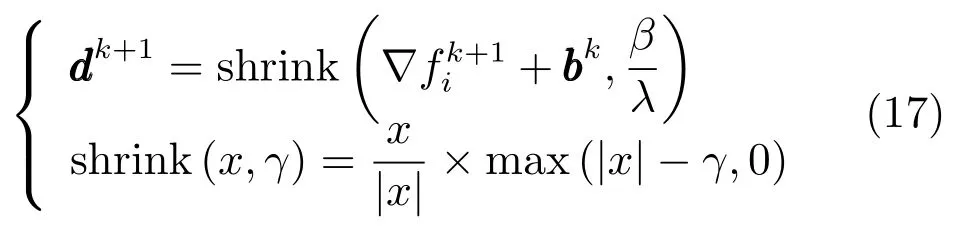
综上所述,融合模型最优解的Split Bregman迭代过程如算法1所示:
算法1.基于变分的图像融合算法
1)将MS图像上采样至Pan分辨率.
2)输入:θ,γ,β,ε=0.05%,i=1,2,3,4.
3)基于MS波段传感器的MTF设计相应的低通滤波器.
4)循环:Fori=1,2,3,4.
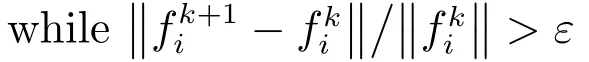
更新计算:
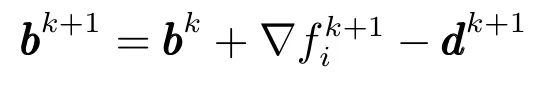
2 实验及分析
2.1 评价指标
由于无法直接获取高分辨率MS图像作为参考,本文对融合图像进行退化并下采样至MS图像分辨率,再与原MS图像进行对比[30].选取空间相关系数sCC[31]、相对整体维数综合误差ERGAS[32]、光谱角映射SAM[33]和无参考图像指标QNR[34]对融合图像质量进行评价.
1)sCC用于评价融合后图像的空间细节信息,定义如下:
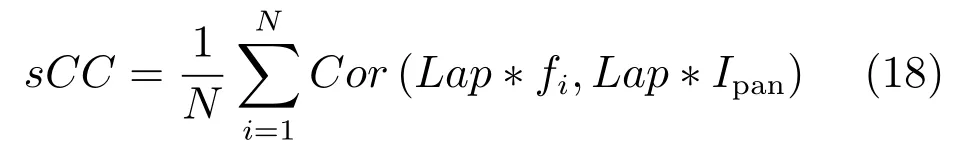
其中,Lap为拉普拉斯滤波器,Cor(·)计算两个波段间相关系数函数,sCC的取值范围在0和1之间,sCC越大,空间细节信息注入越多.
2)ERGAS反映融合图像光谱的失真情况,定义如下:
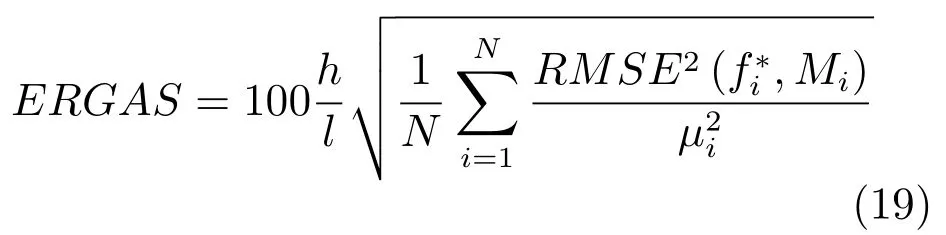
其中,h为Pan图像空间分辨率,l为原MS图像空间分辨率,fi∗是融合图像经MTF设计的低通滤波器滤波并下采样至MS波段分辨率后的退化图像,µi表示图像fi∗的平均灰度,RMSE2(fi∗,Mi)表示图像fi∗与Mi的均方根误差,ERGAS越低,融合图像的光谱质量越好.
3)SAM用来评价融合过程中光谱的扭曲程度:
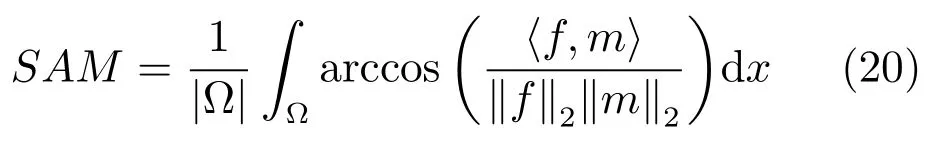
其中,f和m分别为图像fi∗与Mi对应像元上的像素值构成的向量,SAM为光谱矢量间的夹角,SAM越小,表明融合图像的光谱特性保持越好.
4)在无参考图像的情况下,QNR常被用于评测融合图像的综合质量:
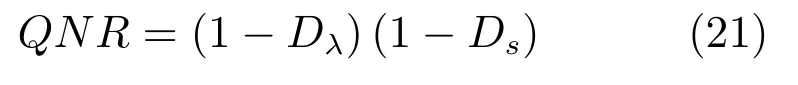
其中,Ds和Dλ分别测量图像的几何结构畸变程度与波段间相关性程度,Ds越小,图像几何结构畸变程度越低,Dλ越越小,波段间的相关性越高.Ds和Dλ分别定义如下:
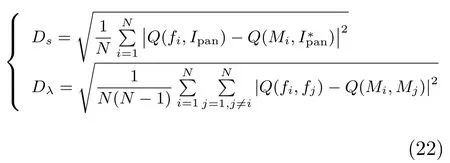
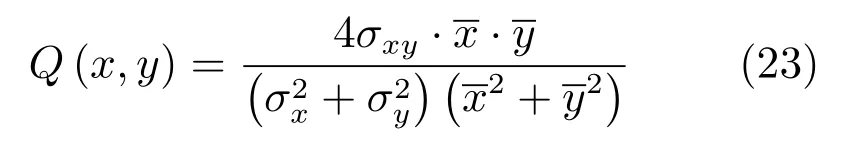
2.2 参数选取
参数θ、γ和β分别为空间细节能量项、光谱保真能量项及正则化能量项对应的权重系数,其取值一般根据启发式规则结合融合实验确定.在分析参数选取对融合结果的影响时,本文选择sCC及ERGAS评价融合图像的空间质量和光谱质量.
从各个能量项的物理意义来看,一般地,θ值越大,空间细节注入越多,sCC将会增大,但可能会出现更高的几何结构畸变和光谱失真.γ值越大,MS融合图像的光谱保持能力越强,ERGAS将会降低,但注入的空间细节将会减少.由于篇幅的限制,本文以QuickBird数据集子图为实验对象,分析不同参数设置对融合结果的影响,逐次遍历参数θ、γ和β并计算相应的sCC和ERGAS,通过分析评价指标随参数的变化趋势,合理选取参数的取值范围.
图2给出了sCC与ERGAS随参数θ、γ和β变化的结果.参数θ和γ的取值范围为[0,10],间隔步长为0.5;参数β为正则化能量项的权重,一般取较小的正值,本文设置其取值范围为[0,0.1],间隔步长为0.01.图2中sCC曲面、ERGAS曲面分别以实线和虚线进行绘制.其中,为便于显示和分析融合指标随参数变化的影响,ERGAS归一化到了[0,1].
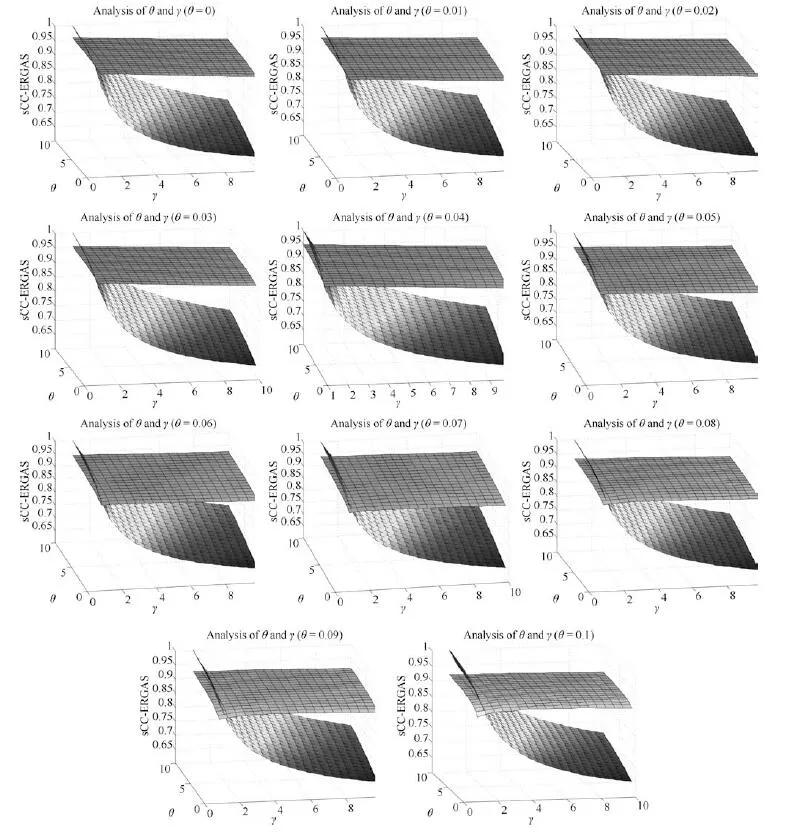
图2 参数对融合结果的分析Fig.2 The analysis of different parameters
从图2可以看出,对于固定的θ,随着γ的增加,sCC与ERGAS将逐渐减小,意味着注入融合图像的空间细节数量逐渐降低,而光谱质量则逐步上升.以β=0.05时为例,当θ=3时,随着γ从1增加至10,sCC的取值从0.9375下降至0.9182,ERGAS取值从1.9259下降至1.3280.其中,当从1增加至5时,ERGAS从1.9259下降至1.4490,下降幅度较大,而当从5增加至10时,ERGAS从1.4490下降至1.3280,下降幅度趋于平缓,考虑到融合图像空间质量和光谱质量的均衡性,参数选取应当满足sCC在尽可能大的同时,ERGAS尽可能的小因此本文设定γ的取值范围为的取值范围为[3,5].对于固定的γ,随着θ的增加,sCC与ERGAS将逐渐增大.以β=0.05时为例,当γ=3时,随着θ的增大,sCC、ERGAS的取值范围分别为[0.9230,0.9407]和[1.479,1.676];当γ=4时,sCC、ERGAS的取值范围分别为[0.9207,0.9386]和[1.4208,1.6118];当γ=5时,sCC、ERGAS的取值范围分别为[0.9185,0.9359]和[1.3789,1.5633].其中,当θ<4时,ERGAS增幅较大,θ>4时,增幅趋于平稳,考虑到在提高融合图像空间质量的同时需要尽可能地保持其光谱特性,本文设定的取值范围为[2,4].在取其他参数值的情况下,sCC和ERGAS随θ及γ的变化趋势基本上与β=0.05时保持一致.β与数值计算的稳定性有关,由于使用了L1正则化,随着参数的增大,算法抑制噪声的能力更强,图像更加平滑,为保证算法数值解的稳定性、提高融合图像的对比度及保持MS图像的光谱特性,参数的取值范围设置为[0.01,0.03].本文在融合实验中取θ=3,γ=5,β=0.02,IKONOS 和 GeoEye-1数据集上的实验结果同样验证了参数的有效性.

图3 IKONOS融合结果Fig.3 Original IKONOS images and pan-sharpening results using different methods
2.3 融合结果分析
为验证模型的有效性,本文选择Quick-Bird、IKONOS及GeoEye-1卫星数据集的全色和多光谱波段图像进行融合实验,并与MTFCON[24]、AWLP[15]、SparseFI[22]、TVR[26]、MTFVariational[25]等算法进行比较.
实验1使用的QuickBird数据下载自http://glcf.umiacs.umd.edu/data/quickbird/.Pan波段和MS波段图像的分辨率分别为0.7m、2.8m.为了更好地展示融合效果,从图像中选取大小为256×256的多植被区域进行展示,融合结果如图3所示.图3(a)为Pan波段图像,图3(b)为上采样至Pan图像分辨率的多光谱RGB波段合成图像,图3(c)为本文算法结果,图3(d)∼(h)分别为 AWLP、SparseFI、TVR、MTF-CON 和MTF-Variational的融合结果,为直观对比各类算法的融合效果,选取大小为25×25的红色边框窗口进行局部放大.从目视效果上来看,TVR与SparseFI算法生成的融合图像空间质量较好,但光谱失真现象明显.MTF-CON算法生成的融合图像光谱失真较小,但图中树木较为模糊.AWLP算法的光谱保持能力较好,并且在空间分辨率的提高上优于MTF-CON算法,但图像清晰度仍有所欠缺.MTF-Variational与本文算法生成的融合图像纹理清晰,且无明显光谱失真现象,对比图3(c)与图3(h)放大区域,本文算法在色彩上与图3(b)更为接近.表3为QuickBird数据集上的定量评价结果,加粗数据为最佳指标值.TVR与SparseFI算法的ERGAS与SAM较高,意味融合图像存在明显的色彩畸变,光谱信息损失较大.MTF-CON的sCC与ERGAS较低,说明融合图像光谱保真度较好,但注入的空间细节相对较少.MTFVariational和本文模型的ERGAS和SAM较为理想,说明基于传感器系统的MTF构建低通滤波器,能够有效降低融合图像的光谱失真程度.其中,MTF-Variational算法的Ds与sCC均高于本文算法,意味着MTF-Variational算法在向MS图像注入更多空间细节的同时,融合图像的空间结构畸变现象更为严重.从表3可知,本文算法在ERGAS、SAM、Ds及QNR等指标上最优,说明本文算法在提升MS波段图像空间质量的同时,有效地保持了其原有的光谱信息.
实验2数据来自2007年3月29日上海地区的IKONOS遥感数据集,其Pan波段和MS波段图像的空间分辨率分别为1m和4m.为了更好地展示融合效果,从图像中选取大小为256×256的中等植被区域进行展示,融合结果如图4所示.从目视效果上看,AWLP与MTF-CON算法光谱保持能力较好,但在植被区域空间细节注入能力不足.SparseFI算法具有较好的空间注入能力,但部分区域出现虚假边缘.TVR算法的融合图像空间细节信息丰富,但光谱失真严重.MTF-Variational与本文算法融合图像清晰,但对比要植被区域可知本文算法光谱保持能力更优.表4为IKONOS数据集上的定量评价结果.TVR算法的sCC、ERGAS及SAM均较高,说明该融合图像在获得较多空间细节的同时产生了较大的光谱失真现象.AWLP、SparseFI及MTF-CON算法的sCC较低,说明上述算法的空间细节注入能力不足.MTF-CON、MTF-Variational与本文算法的ERGAS较为理想,意味着MTF的引入有效增强了算法的光谱保持能力.TVR与MTF-Variational算法的sCC、Ds高于本文算法,说明融合图像在获取较多空间细节的同时,几何结构畸变程度较大.本文算法除sCC外,其他指标均为最优,说明了本文算法融合性能更为均衡.
实验3融合的数据为GeoEye-1卫星在官方网站上提供的遥感影像,Pan波段和MS波段图像的空间分辨率分别为0.5m和2m.为了更好地展示融合效果,从图像中选取大小为256×256的稀疏植被区域进行展示,融合结果如图5所示.从目视效果上来看,MTF-CON算法与AWLP算法均能较好保持图像的光谱信息,但植被在放大区域不够清晰.TVR与SparseFI算法生成的融合图像较为清晰,但光谱失真严重.MTF-Variational与本文算法生成的融合图像视觉效果较好,但光谱保持能力本文算法更高.表5为各融合算法在GeoEye-1数据集上的定量评价结果.TVR的sCC、ERGAS均为最高值,意味融合图像注入过多的空间细节,光谱信息丢失严重.SparseFI算法的SAM、ERGAS较高,sCC、Ds较低,说明融合图像光谱失真明显,但几何结构保持较好.与SparseFI算法相比,本文算法的sCC更高,但Ds更低,表明融合模型在注入更多空间细节的同时,能够更好地保持目标的几何结构.MTF-Variational的sCC及SAM均高与本文算法,说明过量空间细节的注入导致融合图像光谱失真现象更为明显.本文算法除sCC低于TVR算法外,其余指标均为最优,意味着融合模型能够有效地保持图像目标的几何结构和光谱特性.

表3 QuickBird融合结果定量评价Table 3 Quality assessment of the fused images for QuickBird dataset

表4 IKONOS融合结果定量评价Table 4 Quality assessment of the fused images for IKONOS dataset


图5 GeoEye-1融合结果Fig.5 Original GeoEye-1 images and pan-sharpening results using different methods
为了进一步验证算法的有效性,选择加拿大Fredericton地区的IKONOS遥感数据集进行融合实验.该数据集地物信息丰富,含有较多的绿色植被区域,本文从该数据集中分别选取多植被、中等植被及稀疏植被区域进行对比实验,融合结果如图6∼8所示,定量评价指标见表6,加粗数据为最佳指标.从目视效果上来看,在三类区域中,多植被区域光谱失真现象更加明显.SparseFI与MTF-CON算法生成的融合图像在屋顶及草地等低灰度区域空间细节注入不足.TVR算法具有较好的空间细节注入能力,但光谱失真现象严重.AWLP、MTFVariational与本文算法生成的融合图像清晰且光谱失真程度低,对比道路与植被区域可以发现,本文算法生成的融合图像纹理更为丰富,且色彩上与低分辨率MS图像更为接近.从指标上来看,本文算法在不同区域的各项评价指标综合最优.
3 总结
本文提出了一种基于边缘增强与光谱特性保持的变分融合模型,以生成具有高空间分辨率和高光谱分辨率的MS图像.假设在不同尺度下Pan图像与MS图像的线性关系保持不变,通过拟合退化的Pan图像与原MS图像间之间的线性关系定义空间细节能量泛函,提高了MS图像的空间质量.为了更有效地解译MS图像中的感兴趣目标,根据Pan图像的梯度定义边缘增强能量泛函,在MS图像中注入了Pan图像目标的几何结构.为了有效地降低融合过程中MS图像的光谱失真,定义了光谱保真能量泛函,基于多光谱波段传感器的MTF设计低通滤波器,限制了注入MS图像空间细节的数量.变分框架下L1正则化能量项的引入,保证了数值解的稳定性.QuickBird、IKONOS及GeoEye-1数据集上的实验验证了模型的有效性,综合融合性能优于MTF-CON、AWLP、SparseFI、TVR 和MTF-Variational等算法.但模型中权重系数较多,如何自适应地选择权重系数将是下一步的研究方向.
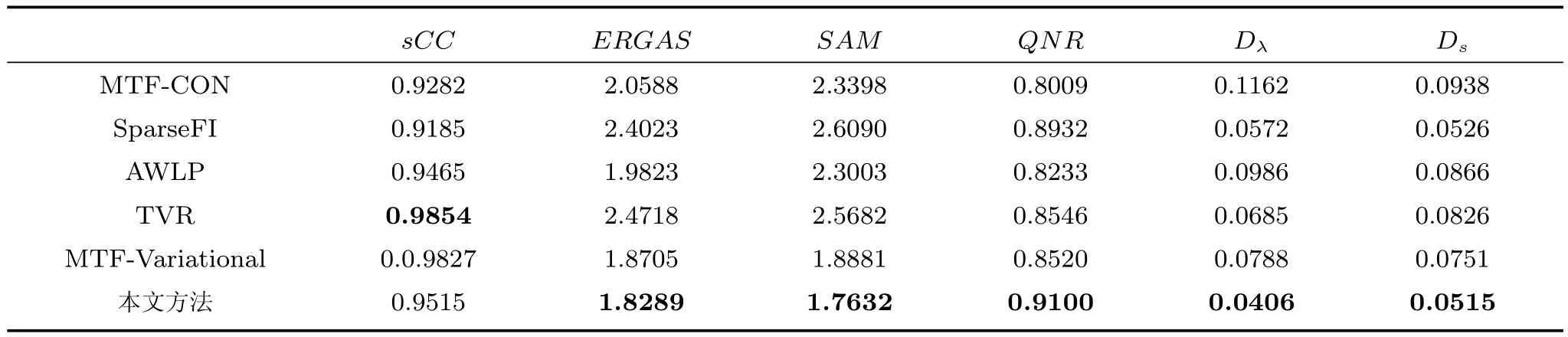
表5 GeoEye-1融合结果定量评价Table 5 Quality assessment of the fused images for GeoEye-1 dataset
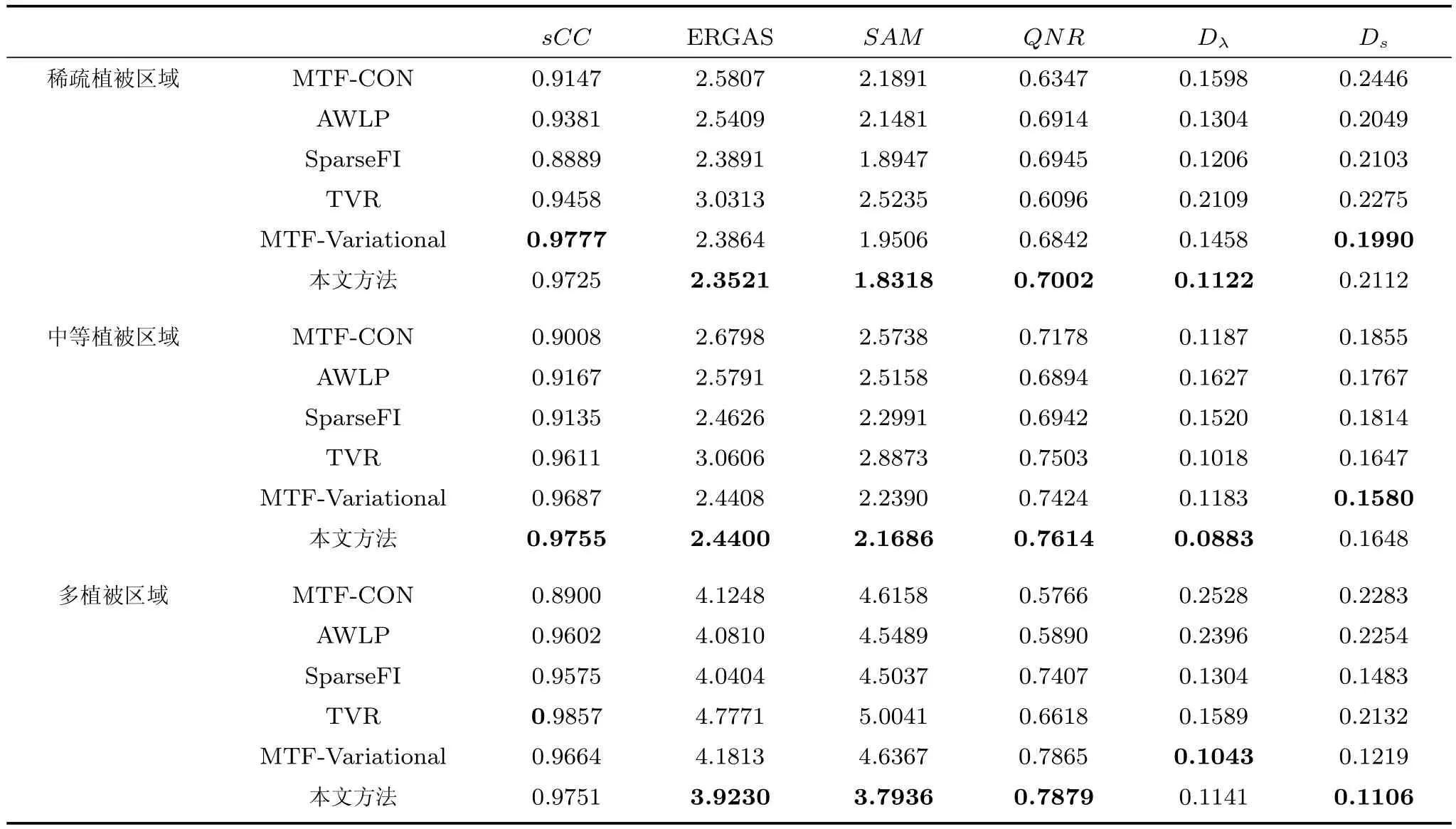
表6 不同植被区域融合结果定量分析Table 6 Quality assessment of different areas of the fused images

图6 稀疏植被区域融合结果对比图Fig.6 Pan-sharpening results of the MS images with sparse vegetated area

图7 中等植被区域融合结果对比图Fig.7 Pan-sharpening results of the MS images with moderate vegetated area

图8 多植被区域融合结果对比图Fig.8 Pan-sharpening results of the MS images with dense vegetated area
