关于梁与刚体接触问题的讨论

吴 晓

(湖南文理学院 机械工程学院，湖南 常德 415000)

1 引 言

梁与刚体接触的问题是工程实际中常见的结构工程问题，所以研究梁弯曲时静态接触压力是有实际工程意义的。文献[1]研究了梁与刚体的接触问题。文献[2]指出，文献[1]讨论的梁与刚体的接触问题，在接触面的中间梁段常常没有作用力，仅在接触面的边界上有集中力互相作用，考虑梁的横向剪切变形后，可以避免发生这种奇怪的现象。文献[3]较好地解决了文献[1]、文献[2]中两端固支梁在分布载荷作用下，梁与刚性基础的接触问题。文献[4]把文献[1]中梁与刚体的接触问题作为习题引入教材，来锻炼提高学生分析问题、解决问题的能力。因此，非常有必要对文献[1-2]中梁与刚体的接触问题进行深入讨论，来解释文献[2]所指出的文献[1]中存在的奇怪现象。

2 梁与刚体的接触问题

(1)

由式(1)可以求得：

(2)

(3)

图1 悬臂梁与刚体接触图

所以，梁在集中力P作用下与圆柱刚体紧密贴合时的挠度为：

(4)

由材料力学可知，梁与圆柱刚体紧密贴合时的弯曲微分方程为：

(5)

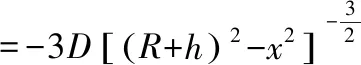
(6)

式中，0≤x≤ξ。

高中数学新课程的教学和传统的教学思想和教学方法相比，在适应学生的个性化学习需求等方面发生了根本性变化.在教学中教师必须转换教学思想和教学观念，树立学生为本的教学理念.实现由知识的传授者向引导者转变.在高中数学教学中，教师是教学活动的引导者，是知识的传授者，掌握着教学活动的主动权，所以教师必须转变教学观念,优化传统的教学方式，数学文化的渗透需要教师具备丰富的数学文化知识,这就要求教师要加强自我学习，全面地掌握与数学课程相关的数学文化、数学大家的生平介绍、数学人文历史等一系列的知识，这样才能在教导学生的过程中合理渗透,才能提高学生的文化素养.

w2=θD(l-ξ)

(7)

(8)

所以，图1所示悬臂梁在较大集中力作用下，梁自由端的挠度为：

w(ξ)=w1(ξ)+w2+w3

(9)

(10)

式(10)与文献[1]、文献[4]给出的结果是一致的。把式(4)展开成以下形式：

(11)

把式(11)代入式(5)中，可得梁与圆柱刚体的接触压力为：

(12)

(0≤x≤η)

(13)

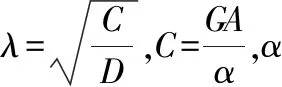
3 计算分析及讨论

式(11)是式(4)简化后的结果，在式(11)中若保留前两项代入式(5)中，可知图1所示梁与刚体接触处之间梁段接触压力为常量。如把式(11)代入式(5)中，可知图1所示梁与刚体接触处之间梁段接触压力表达式为式(12)。

下面把式(6)、式(12)、式(13)计算出的压力曲线画在图2中，以便分析讨论。

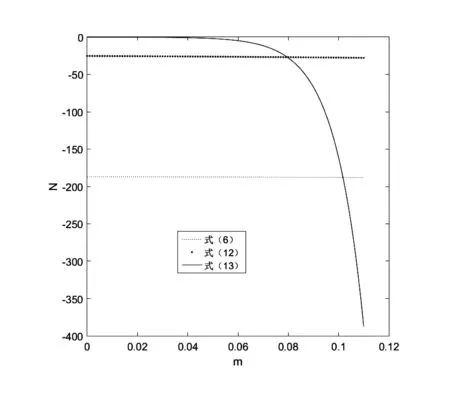
图2 悬臂梁与刚体的接触压力曲线

由图2可以看出，式(13)(文献[2]解)计算出的接触压力曲线在0～0.04(m)梁段间的接触压力几乎为零，在接触处的接触压力为-105250N/m，这显然是不合理的。由图2可以看出，式(12)计算出的接触压力曲线是平缓递增的，式(6)计算出的接触压力曲线也是平缓递增的，这说明悬臂梁与刚体的接触压力近似均布压力，但式(6)计算结果与式(12)计算结果的误差较大，这主要是仅取式(4)简化结果的前四项导致的。取式(4)简化结果的高阶项虽可提高计算精度，同时也会增大计算量。因此，计算悬臂梁与刚体的接触压力时，笔者建议采用本文式(6)来计算。

4 结 论

从以上分析讨论可得以下结论：

(1)梁与刚体的接触问题是一个非线性问题。

(2)本文解释了文献[2]指出的文献[1]中存在的奇怪现象：“在接触面的中间梁段常常没有作用力，而仅在接触面的边界上有集中力互相作用。”

(3)计算梁自由端的挠度时，可以对非线性项进行线性简化。计算梁与刚体接触处之间梁段接触压力时，对非线性项进行线性简化是不合适的。