基于Abaqus的齿轮传动系统模态分析

郑 岩，李 颖

(1.吉林省建研科技有限责任公司，吉林 长春 130000；2.长春理工大学，吉林 长春 130000)

1 引 言

齿轮传动系统是由齿轮、转子和轴承等组成的传动系统，研究其动力学特性就是为了确定和评价齿轮传动系统的动态性能，找出导致系统振动超限的因素，并进行优化，同时也为设计高质量的齿轮传动系统提供理论上的指导。

齿轮传动系统的固有特性是指固有频率以及相应的振型，是其最基本的动态特性之一，对系统的动载及振动形式等均有显著的影响。对于齿轮传动系统固有特性的研究，目前最为有效的方法是基于有限元法的模态分析[1-3]。

2 模态分析基本理论

物理参数分析模型通常为多个广义坐标相互耦合的二阶常微分方程组，这种微分方程组不易求解。通常采用坐标变换的方法，使方程组解耦，成为一组以模态坐标及模态参数描述的非耦合方程，以便于对其进行求解，这种方法即为模态分析法。坐标变换矩阵为模态矩阵，其每列为模态振型。模态分析中，采用了模态截断的处理方法，可以很大程度地减少方程数目和计算容量，计算成本较低[4-5]。

时域和频域内均可采用模态分析法，其目标是提取系统的模态参数，为系统的振动特性分析以及结构动力学特性的优化、设计等提供依据。

对于多自由度无阻尼自由振动系统，其运动方程为：

(1)

此系统中存在N个固有频率及对应主振型，每一对固有频率和振型代表一个单自由度自由振动系统。这种在自由振动时结构所具有的基本振动特性即为结构的模态。多自由度系统的自由振动可以分解为N个固有模态振动的叠加。一般来说，多自由度系统是做多个固有频率的简谐振动的合成振动。

设多自由度自由振动系统中某一简谐振动形式的解为：

(2)

则有：

(3)

将式(2)、式(3)代入式(1)，得出特征方程：

(4)

|([K]-ω2[M])|=0

(5)

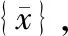
根据有限元理论，可得系统的分析模型：

(6)

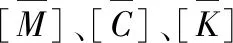
[φ]=[φ1,φ2,φ3……,φn]

(7)

则有：

[φ]T[M][φ]=[I]

(8)

(9)

若设[C]=[0]，即对多自由度无阻尼振动系统，式(6)可化为：

(10)

式中，[φ]即模态矩阵，{Q(t)}=[φ]T{p(t)}称为模态载荷列阵，[I]称为模态质量矩阵，[Ω2]称为模态刚度矩阵，[q]称为模态坐标。

3 基于Abaqus的齿轮传动系统模态分析

(1)启动Abaqus/CAE导入分析模型

基于Creo4.0软件的特征建模技术和参数化建模技术建立齿轮传动系统的参数化模型，包括外啮合直齿圆柱齿轮和轴的参数化建模。建立的齿轮传动系统参数化模型见图1，Abaqus/CAE模型文件导入界面和齿轮传动系统运动简图如图2、图3所示。

图1 齿轮传动系统的参数化模型

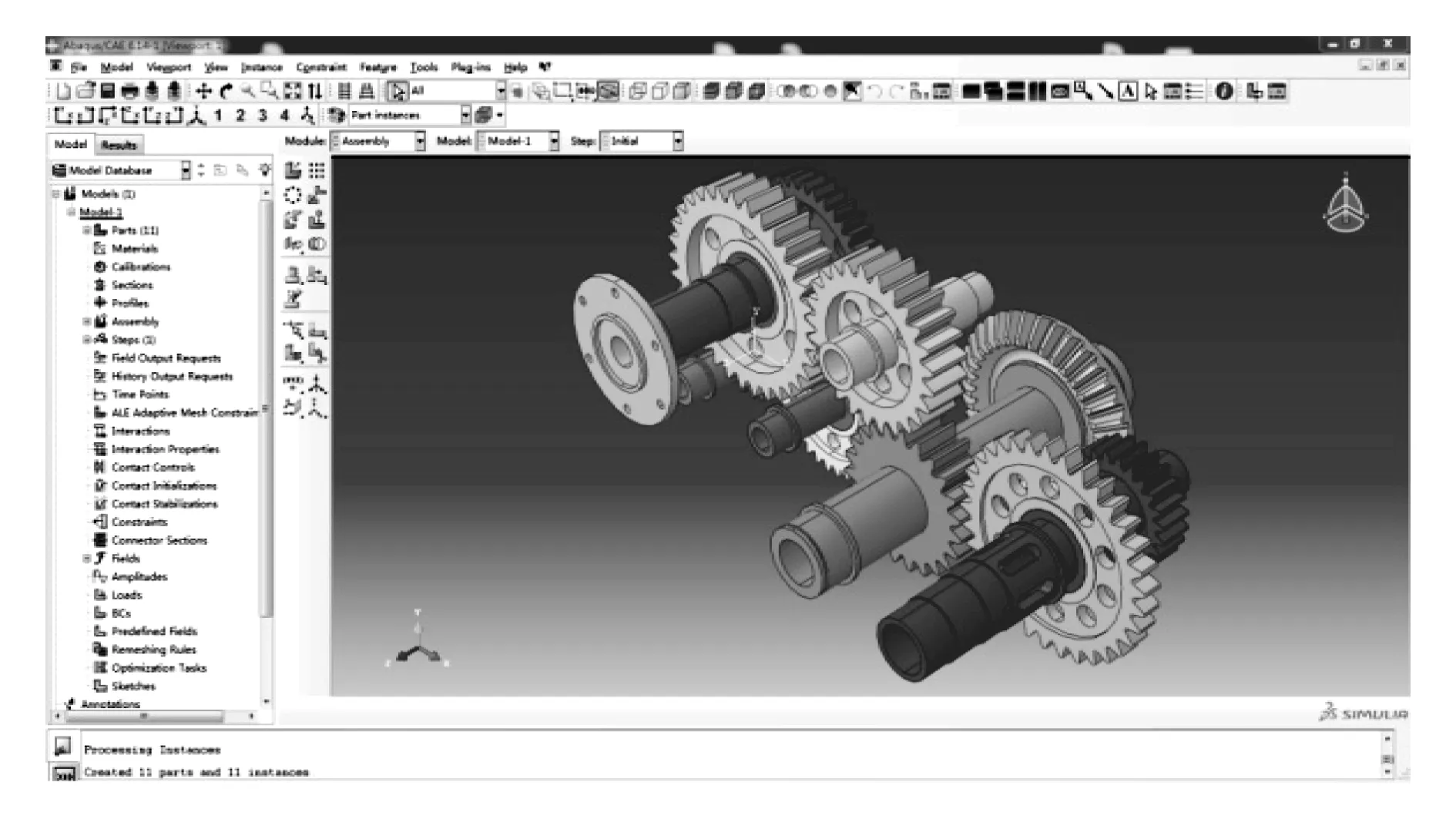
图2 Abaqus/CAE模型文件导入界面

(2)设置材料属性

齿轮传动系统齿轮材料选用高级优质合金结构钢12Cr2Ni4A，材料参数如表1所示。

表1 齿轮传动系统材料参数

(3)定义频率提取分析

在分析步设置模块，选择Procedure type类型为“线性扰动：频率提取”分析步，求解器类型选择为Lanczos，在Number of eigenvalues requested后选择Value，并输入特征值数目20，默认其他选项，完成分析步设置。

(4)定义接触

完成接触属性的定义，选择“Hard”Contact，其他选项默认；并且在Contact Property选项卡中Global Property assignment指定为上步所创建的接触属性。

(5)施加边界条件及载荷

在模态分析中，载荷对其没有影响，只有边界条件对系统有影响，所以仅施加边界条件。施加边界条件后使传动系的各轴仅具有一个绕Z轴的旋转自由度。图4为齿轮传动系统边界条件的施加位置和方向。

图4 齿轮传动系统边界条件的施加位置及方向

(6)分网

进行网格划分时，首先需要布种子，设置Approximate global size为5.0，单元类型选择修正的二次Tet单元(C3D10M)，并选择自由分网技术，网格模型如图5所示。

图5 齿轮传动系统网格模型

(7)提交分析作业及后处理

采用Lanczos算法求解齿轮传动系统前10阶模态频率及模态振型情况，见表2，图6给出了齿轮传动系统的前10阶模态。

表2 齿轮传动系统前10阶模态频率及振型

(a)第1阶模态

(b)第2阶模态

(e)第5阶模态

(f)第6阶模态

(g)第7阶模态

(h)第8阶模态

(i)第9阶模态

(j)第10阶模态

在忽略外部激励对系统的影响，仅考虑含内部激励作用的齿轮系统主共振响应特性的情况下，齿轮传动系统的激励频率主要为啮合频率。齿轮传动系统的啮合频率为P=nZ/60，其中，n为齿轮轴转速(r/min)，Z为齿轮轮齿数目。现分别计算该齿轮传动系统各级齿轮副的啮合频率，如表3所示。啮合频率远离系统的前10阶模态频率(前10阶模态最高模态频率为2110.9Hz，见表2)，故附件传动系统在啮合频率的激励下不会产生图6所示模态振型，所以不会发生共振。

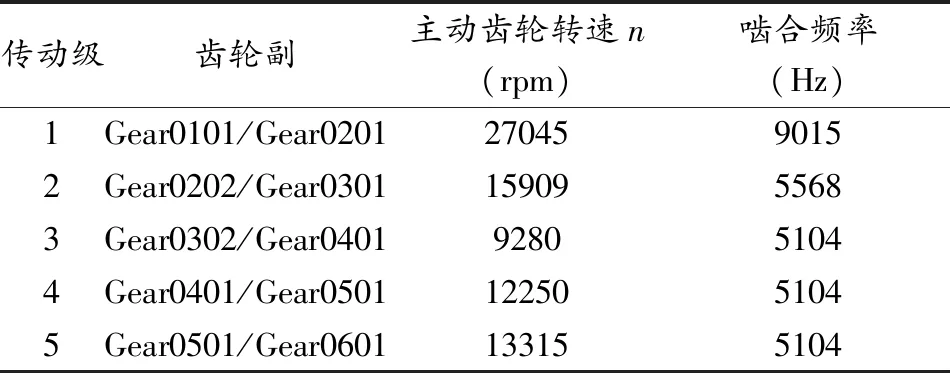
表3 齿轮传动系统各级齿轮副的啮合频率

4 结 论

针对试验机等设备研究过程中常需要对齿轮传动系统进行动力分析，借助Abaqus有限元软件对齿轮传动系统进行模态分析，是一种基于结构动力学的模态分析方法。虽然这种方法为大多数学者所采用，但是由于齿轮系统是高速旋转件，而转速对系统模态有很大影响，这种方法存在一定的误差。本文基于结构动力学的模态分析，得到了附件传动系统的前10阶模态频率及相应振型，在忽略外部激励，仅考虑含内部激励作用的齿轮系统模态分析的结果表明，齿轮传动系统的啮合频率远离齿轮传动系统的前10阶模态频率，不会产生前10阶模态振型，所以不会产生共振。

基于齿轮传动系统中齿轮实体样机，对其进行有限元模态分析。通过对齿轮传动系统的参数化建模，调整模型参数，分析不同参数时齿轮传动系统的动态性能，为齿轮系统的性能优化提供指导。参数化的齿轮系统模型还能在性能优化之后，根据相应的优化参数做出相应调整，为设计高质量的齿轮传动系统奠定基础。