基于空间曲面插值的机翼形变实时显示方法研究

侯乔乔，张清勇

(中国飞机强度研究所 第八研究室，陕西 西安 710065)

1 引 言

全机静力试验虚拟机翼形变在高载荷的试验工况中有着现实的应用需求。高载试验情况下，整个机体的储能高达1MJ以上。如果发生破坏，能量以不可控的形式释放出来，会对试验人员的安全构成很大威胁。基于试验数据驱动的虚拟显示系统，能够让试验技术人员在安全的区域对飞机的整体变形情况进行观察。实际上，基于数据驱动的实时显示技术在三维地图可视化[1-5]、电影与动画制作[6-7]等方面有着广泛的应用。以往的静力试验中，试验人员所关心的测量点的数据只能以表格或二维曲线的形式实时显示，缺乏直观性和整体性。参试人员需要冒险近距离观察，以便对试验情况进行整体把握。

为了实时掌握试验件的变形情况及保障试验人员的安全，研究一种能够实时、动态显示试验件变形的方法是必要的。文章通过借鉴电影动画制作、三维地图可视化的相关技术，以试验数据作为驱动，获得了全机静力试验机翼变形情况的实时显示方法。必要时，可在全机静力试验的高载工况中应用。

2 机体曲面构造的方法

为了能够显示试验过程中机体的变化过程，首先需要构造一个等比例的机体曲面。根据实际情况的需要，曲面可以是完整的，也可以是局部的。曲面的静态数据来源于支撑曲面的数模离散点的三维坐标，其“精细”程度取决于离散点的位置与数量，而曲面的形变情况则依靠测量点的位移量来驱动实现。

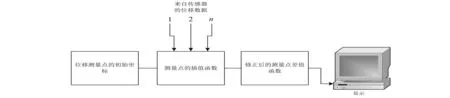
图1 实时显示流程图

设机体数模所在区域为U，在U内构造函数p(x,y)，使得在节点处有zi=p(xi,yi)。为此，将插值区域划分成一个个三角形片区ui(i=1,2,…,n-2)，ui为U的子集且满足：

插值区域划分及差值函数构造图如图2所示。

图2 插值区域划分及差值函数构造图

区域U内共有n个节点，则需要n-2个三角形可做到对区域U的全覆盖[8]。为了保证在三角区域边界上的连续性，采用x,y的线性函数作为插值函数，记为：

(1)

于是，机翼曲面可近似表示为n-2个线性无关(由于机翼表面不可能是平面，所以4个节点不可能共面)的二元一次多项式的线性组合。

(2)

即在ui内：z=pi(x,y),z=pj(x,y)=0,(i≠j)。

3 算 例

以某型机某工况测得的数据为例，共有12个测量点，分布在右侧机翼下方。编号及初始坐标如表1所示，加载级数与测量点z方向位移量见表2。

表1 下翼面测量点坐标

表2 加载级数与测量点z方向位移量/mm

将测量点的初始坐标写成n×3矩阵形式：

(3)

则到达第j个加载级时，各测量点的坐标为：

(4)

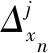
图3显示了右侧机翼在初始状态与第7级载荷作用下的位置。其中，分布在机翼边缘的“o”为位移测量点，即插值节点。可以看出，机翼根部重合，翼尖发生了明显的分离。

4 结论与展望

由插值函数的特点可知，在插值节点(xi,yi,zi)，(i=1,2,…,n)处，插值曲面与机翼真实曲面是吻合的，在非节点处有一定的偏离，偏离程度取决于节点的密度以及所采用的插值方法。图例中节点是散乱的(即没有分布在等间距的网格上)，采用的是三节点线性插值，在三角节点边界处连续但一

图3 机翼初始与第7级载荷下位置图

阶导不连续。对显示机翼整体位置来说，节点处是吻合的，影响不大。采用三次及以上多项式插值不能保证边界处的连续性，且曲面上会出现明显的“鼓包”，所以不宜采用高次插值。若需要进一步增加插值精度，可在肋与长桁的方向上适当增加节点个数。

为了考察测量点数量即插值点数量对模拟结果精度的影响，将机翼前梁由内向外第5个点去掉，在第10级载荷下插值得到此点的位移与实际测量值相差约65mm，相对误差为65/685=9.5%，对于做实时显示之用途来说，此误差可以接受。