函数与导数的综合应用测试题（A卷）

■河南省许昌高级中学 何晓亚

一、选择题

1.曲线y=ex—l nx在点(1，e)处的切线方程为( )。

A.(1—e)x—y+1=0

B.(1—e)x—y—1=0

C.(e—1)x—y+1=0

D.(e—1)x—y—1=0

2.已知f "(x)为f(x)的导函数，则f "(x)的图像是图1中的( )。

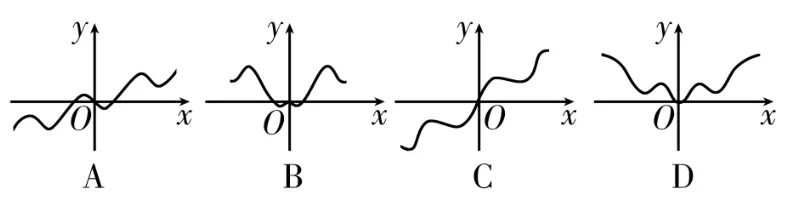
图1

3.已知f(x)=l nx，g(x)=＜0)，直线l与函数f(x)，g(x)的图像都相切，且与f(x)图像的切点为(1，f(1))，则m的值为( )。

A.—1 B.—3

C.—4 D.—2

4.下列函数中，在(0，+∞)上为增函数的是( )。

A.f(x)=s i n2x

B.f(x)=xex

C.f(x)=x3—x

D.f(x)=—x+l nx

5.已知函数f(x)=x3+a x+4，则“a＞0”是“f(x)在R上单调递增”的( )。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

6.若函数f(x)=x3—x2+a x—5在区间[—1，2]上不单调，则实数a的取值范围是( )。

A.(—∞，—3]

B.(—3，1)

C.[1，+∞)

D.(—∞，—3]∪[1，+∞)

7.函数f(x)=—x+l nx在区间(0，e]上的最大值为( )。

A.1—e B.—1

C.—e D.0

8.若函数f(x)=x3—2c x2+x有极值点，则实数c的取值范围为( )。

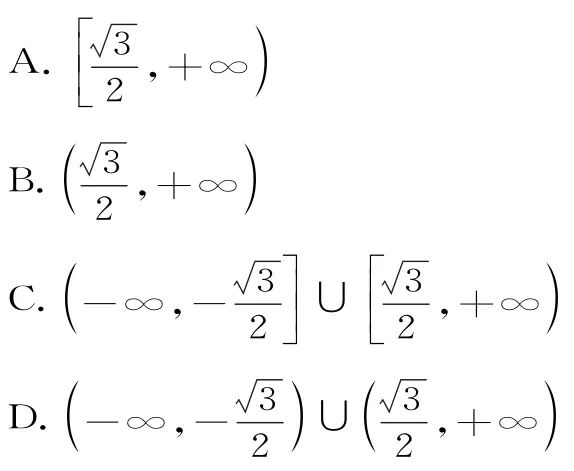
9.设直线x=t与函数h(x)=x2，g(x)=l nx的图像分别交于点M，N，则当|MN|取最小值时t的值为( )。

1 0.若不等式2xl nx≥—x2+a x—3恒成立，则实数a的取值范围为( )。

A.(—∞，0)

B.(—∞，4]

C.(0，+∞)

D.[4，+∞)

1 1.已知y=f(x)为R上的连续可导函数，且x f "(x)+f(x)＞0，则函数g(x)=x f(x)+1(x＞0)的零点个数为( )。

A.0 B.1

C.0或1 D.无数个

1 2.设f "(x)是函数f(x)(x∈R)的导函数，f(0)=1，且3f(x)=f "(x)—3，则4f(x)＞f "(x)的解集是( )。

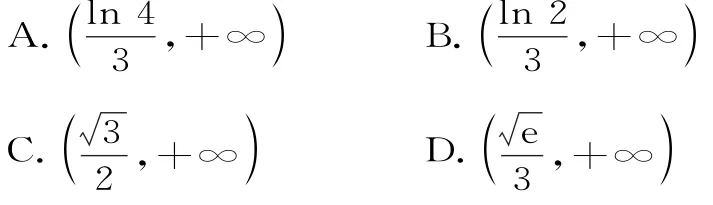
二、填空题

1 3.若函数f(x)=2a x3—6x2+7在(0，2]上是单调递减函数，则实数a的取值范围是____。

1 4.已知函数f(x)=x3+3x2—9x+1，若f(x)在区间[k，2]上的最大值为2 8，则实数k的取值范围为____。

1 5.展开式的中间项系数为2 0，图2中的阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形，则封闭图形的面积S=____。

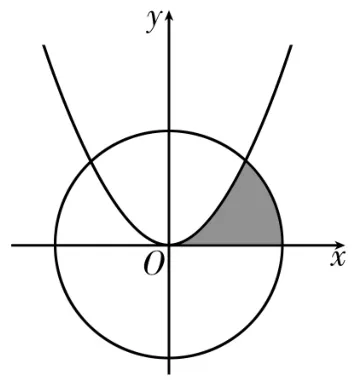
图2

1 6.定义域为R的可导函数y=f(x)的导函数为f "(x)，满足f(x)＞f "(x)，且f(0)=1，则不等式＜1的解集为____。

三、解答题

1 7.已知函数f(x)=x3+(1—a)x2—a(a+2)x+b(a，b∈R)。

(1)若函数f(x)的图像过原点，且在原点处的切线斜率为—3，求a，b的值；

(2)若曲线y=f(x)存在两条垂直于y轴的切线，求a的取值范围。

1 8.已知函数f(x)=al nx+(a+1)x+3。

(1)当a=—1时，求函数f(x)的单调递减区间；

(2)若函数f(x)在区间(0，+∞)上是增函数，求实数a的取值范围。

1 9.已知二次函数f(x)的最小值为—4，且关于x的不等式f(x)≤0的解集为{x|—1≤x≤3，x∈R}。

(1)求函数f(x)的解析式；

2 0.已知函数f(x)=l nx+1)x。

(1)若曲线y=f(x)在x=1处的切线方程为y=—2，求f(x)的单调区间；

(2)当x＞0时，恒成立，求实数a的取值范围。

2 1.已知函数f(x)=ex(ex—a)—a2x，其中参数a≤0。

(1)讨论f(x)的单调性；

(2)若f(x)≥0，求a的取值范围。

2 2.已知函数f(x)=l nx，g(x)=—b x(b为常数)。

(1)函数f(x)的图像在点(1，f(1))处的切线与g(x)的图像相切，求实数b的值；

(2)设h(x)=f(x)+g(x)，若函数h(x)在定义域上存在单调递减区间，求实数b的取值范围；

(3)若b＞1，对于区间[1，2]上的任意两个不相等的实数x1，x2都有|f(x1)—f(x2)|＞|g(x1)—g(x2)|成立，求b的取值范围。