Compact passing algorithm for signalized intersection management based on vehicular network
2019-04-04BianChentongYinGuodongXuLiweiZhangNing
Bian Chentong Yin Guodong Xu Liwei Zhang Ning
(School of Mechanical Engineering, Southeast University, Nanjing 211189, China)
Abstract:To improve the traffic efficiency at signalized intersections, a compact passing algorithm is proposed based on a vehicular network. Its basic principle is that several waiting vehicles after the stop line of the considered intersection should simultaneously start in green periods. Thus, more vehicles can pass the intersection in a green period. Then, the having passed vehicles should follow the planned trajectories to enlarge their longitudinal clearances. Phase timing is not considered in the compact passing algorithm, and therefore, the proposed compact passing algorithm can be combined with other algorithms on phase timing to further improve their performances. Several simulations were designed and performed to verify the performance of the proposed algorithm. The simulation results show that the proposed algorithm can increase the number of completed vehicles and decrease the travel time in the signalized intersections managed by fixed-time and vehicle actuated algorithms, which indicates that the proposed algorithm is effective for improving the traffic efficiency at common signalized intersections.
Key words:intersection management; signalized intersection; vehicular network; compact passing; phase timing
Intersection management is crucial for the efficiency of traffic systems. With the increasing number of vehicles in modern cities, a massive amount of time is wasted due to the low efficiency of conventional intersections. A variety of algorithms have been investigated to improve the traffic efficiency of intersections. These algorithms can be classified into two types. The first one is the signal-based algorithms[1]proposed for signalized intersections and focused on the coordination of traffic flows by traffic signals. These algorithms include the vehicle actuated algorithm[2-3], fuzzy logic control[4-6], Q-learning[7], reinforcement learning[8], adaptive control[9], neural network[10-11], etc. The second one is the signal-free algorithms[12]investigated for un-signalized intersections and focused on the coordination of individual vehicles. These algorithms include the multi-agent algorithm[13], market(or auction) based algorithm[14-15], adaptive cruise control[16], genetic algorithm[17], linear programming[18], etc. The aforementioned studies on intersection management are useful and effective. Generally, signal-free algorithms are more efficient under low traffic load. Under high traffic load, it is more effective to manage intersections using signal-based methods.
This study aims to improve the traffic efficiency of signalized intersections. In conventional signalized intersections, during a green period, vehicles after the stop line will not start at the same time. The main reason is that, it is easy to stop a vehicle behind a stopped vehicle with a narrow front clearance. However, it is very difficult for a driver to maintain a narrow front clearance after a moving vehicle. During a red period, vehicles are stopped behind the stop line with narrow clearances. In a green period, a vehicle will not start when there is not a specific front clearance. In other words, for conventional signalized intersections, a vehicle has to wait for a certain time after the starts of front vehicles, which leads to inefficiency of the utilization of a green period. If several waiting vehicles can simultaneously start and maintain narrow clearances to pass an intersection, more vehicles are expected to pass the intersection in a green period. Meanwhile, most of the previous algorithms on signalized intersections were focused on phase timing. Few of these algorithms considered the starts of waiting vehicles at signalized intersections.
In this paper, the starts of waiting vehicles at signalized intersections are considered. A compact passing algorithm is proposed for the management of signalized intersections. Based on the proposed algorithm, several waiting vehicles can simultaneously start and maintain narrow clearances to pass the considered intersection, which is effective for increasing the count of completed vehicles in a green period and for improving traffic efficiency. The proposed algorithm consists of a simultaneous starting algorithm and a uniform expending algorithm, which are constructed to plan the trajectories of waiting vehicles. There are two stages for waiting vehicles to pass the considered intersection. In the first stage, the simultaneous starting algorithm is used to control several waiting vehicles when passing the intersection at a synchronous speed. In the second stage, the uniform expending algorithm is utilized to enlarge the clearances among the passing vehicles.
1 Problem Statement
The layout of the considered signalized intersection is shown in Fig.1. There are four roads in this intersection. Vehicles move on the right side of these roads. In each road, there are two through lanes and one left-turn lane. Note that, since right-turn vehicles can directly turn right at right-turn lanes without stopping, the right-turn lanes of the intersection are ignored to simplify the problem. The considered intersection includes an intersection management unit (IMU) which is responsible for controlling the traffic lights and planning suitable trajectories for approaching vehicles to pass the intersection. The considered vehicles are equipped with autonomous driving systems, which can follow the trajectories planned by the intersection management systems. At the intersection, the vehicles are controlled by the corresponding autonomous driving systems. After the intersection, a vehicle driver may take over the control of the autonomous driving system depending on the will of the driver. The communication between the IMU and vehicles can be achieved based on vehicular network.
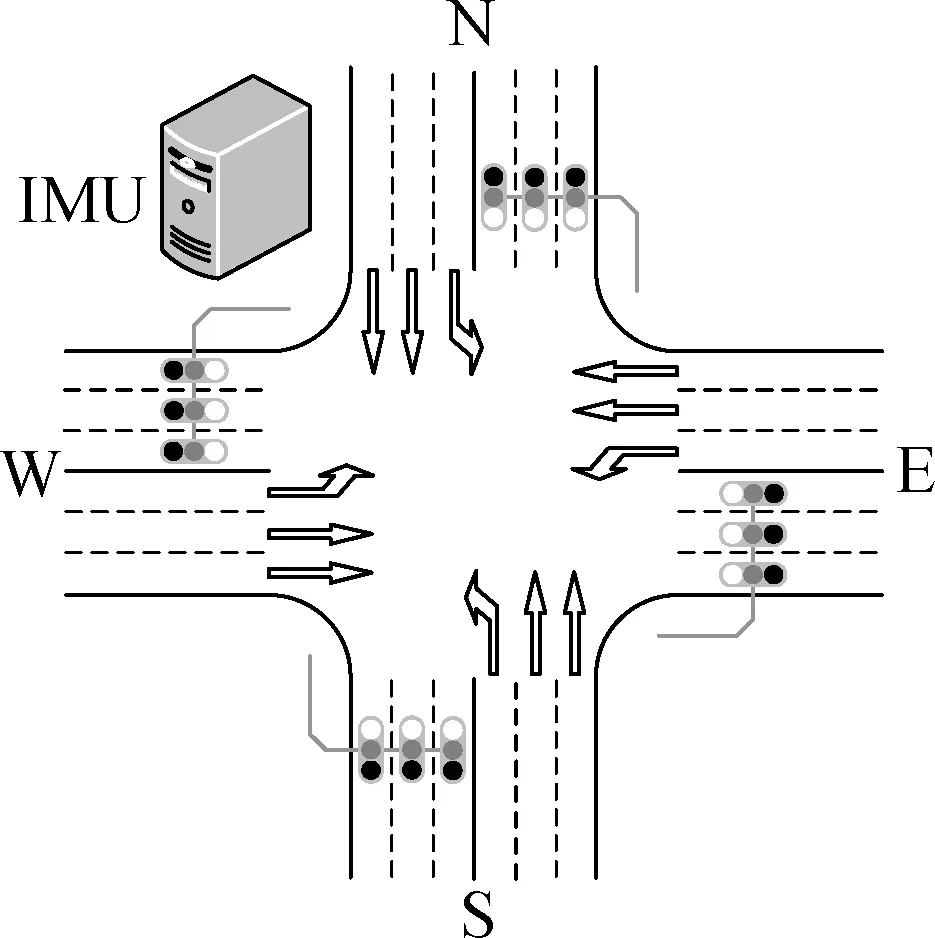
Fig.1 Layout of the considered intersection
2 Compact Passing Algorithm
In this section, the compact passing algorithm is proposed for the management of signalized intersections. First, the initial ideal of the proposed algorithm is shown to demonstrate the kernel of the algorithm. Next, the trajectory planning method for simultaneous starting is shown. Then, the trajectory planning method for uniform expanding is presented. Finally, the process of the proposed compact passing algorithm is introduced based on the simultaneous starting and the uniform expanding algorithms.
2.1 Basic Principle of the algorithm
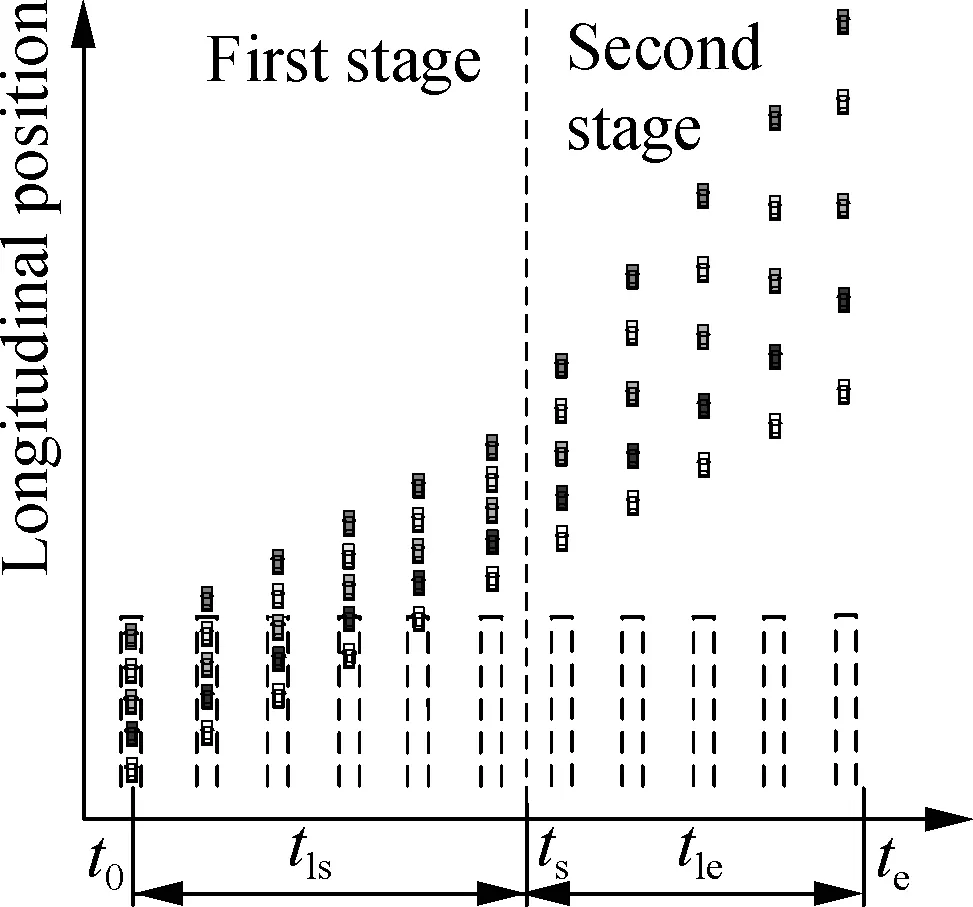
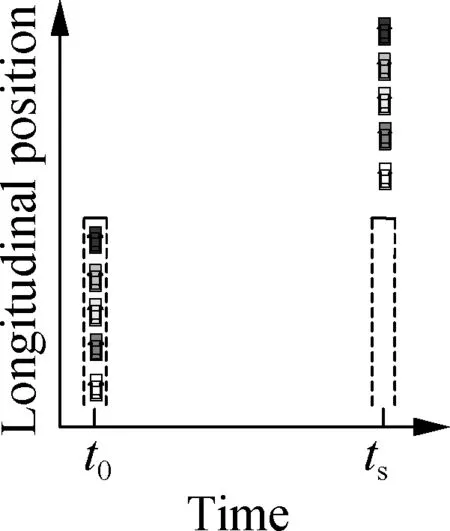
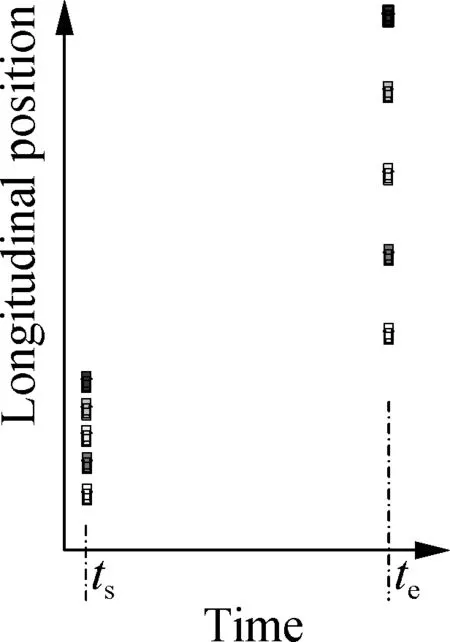
Consider the waiting vehicles shown in Fig.2(a). For conventional signal-based algorithms, during a green period, these vehicles will start when there are sufficient front clearances as indicated in Fig.2(b), wheretg,sandtg,eare the start and end times of a green period. If these vehicles can simultaneously start and pass the intersection as illustrated in Fig.2(c), these vehicles can pass the intersection within a shorter time. To simplify the figure, only five vehicles are plotted. If there are more waiting vehicles in the lane, more vehicles can pass the intersection by maintaining narrow longitudinal clearances within a green period. Thus, the traffic efficiency of the intersection can be improved.
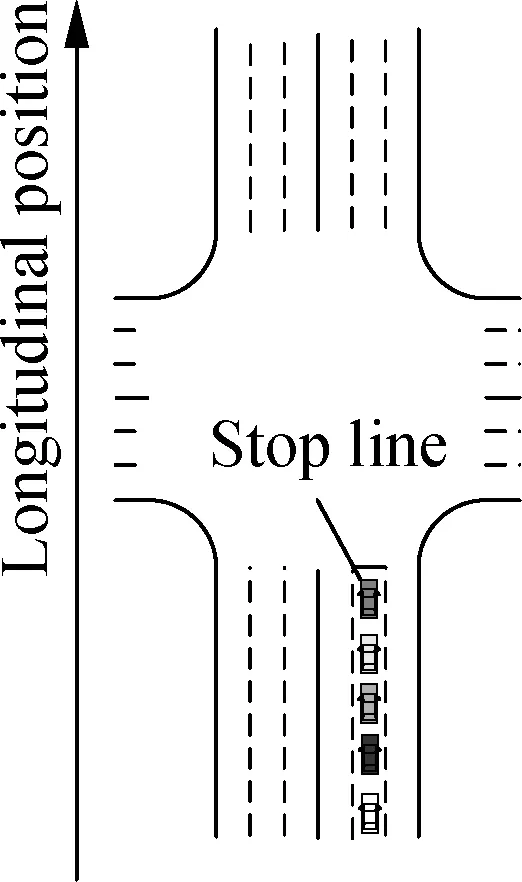
(a)
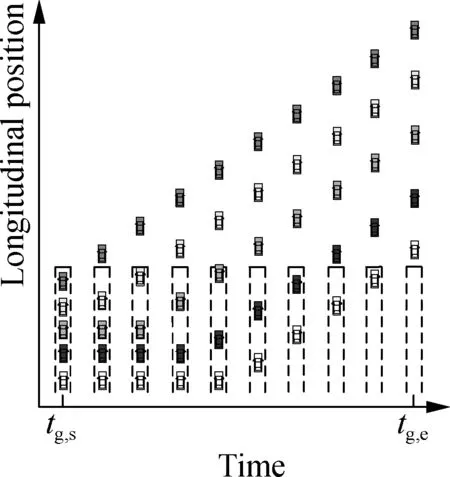
(b)
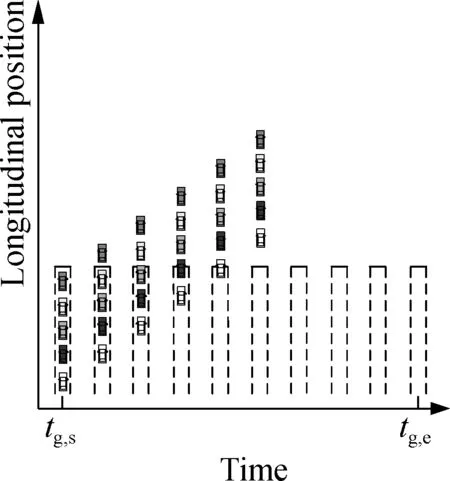
(c)
(d)
A vehicle driver may hope to control the vehicles after the intersection instead of using the autonomous driving system in all roads. To facilitate vehicle drivers and improve safety, after the intersection, the clearances between vehicles should be enlarged. Thus, the routes of vehicles at the intersection are divided into two stages to simplify the problem of intersection management as shown in Fig.2(d). The first stage is simultaneous starting betweent0andtswith the time span oftls, during which the waiting vehicles simultaneously start to pass the intersection. In this stage, all vehicles pass the intersection at a synchronous speed with the foremost vehicle. The second stage is uniform expanding betweentsandtewith the time span oftle, during which these vehicles are coordinated to enlarge the clearances between vehicles. The division of the passing routes is made to simplify the trajectory planning of intersection management. In the first stage, the vehicles can pass the considered intersection with narrow clearances. In the second stage, the clearances of vehicles can be enlarged. To facilitate the discussion, the vehicles that can simultaneously start and pass the intersection are called compact passing vehicles.
2.2 Trajectory planning for simultaneous starting
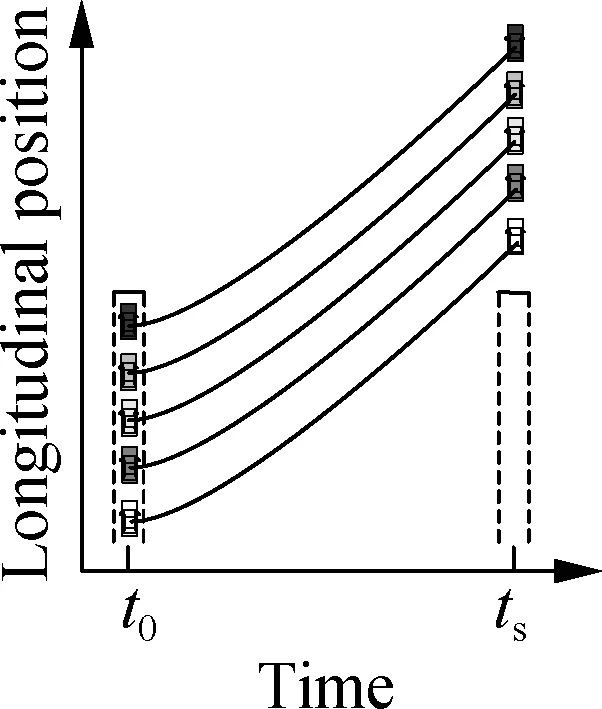
During the green periods, several waiting vehicles should simultaneously start to maintain narrow clearances. The problem of simultaneous starting is shown in Fig.3(a). It is desired for these waiting vehicles to pass the intersection with narrow clearances, which can be achieved by two-step trajectory planning. The first step is to plan the trajectory of the foremost vehicle. For the foremost vehicle, there is no vehicle in front. Thus, the trajectory of the foremost vehicle can be planned as a normal driving maneuver[19]as indicated in Fig.3(b). At the end of this stage, the speed of the foremost vehicle should be of the desired speed which is the mean speed of the traffic flow. The second step is to plan the trajectories of the following vehicles. To maintain narrow clearances between these vehicles, their trajectories can be planned based on the trajectory of the foremost vehicle and the initial positions as indicated in Fig.3(c).
(a)

(b)
(b)
In the second step, the trajectories of the vehicles behind the foremost vehicle can be planned by taking offset of the trajectory of the foremost vehicle. Consider vehicleiafter the foremost vehicle. The trajectory of vehicleican be planned as
si(t)=sf,v(t)-di
(1)
wheretis the time;sf,v(t) is the longitudinal trajectory of the foremost vehicle;si(t) is the planned trajectory of vehiclei;diis the initial distance between the two vehicles. Eq.(1) means that vehicleishould maintain a constant clearance with the foremost vehicle. Provided that the vehicles behind the foremost vehicle can maintain a constant distance with the foremost vehicle, these vehicles can pass the intersection as indicated in Fig.3(c).
2.3 Trajectory planning for uniform expending
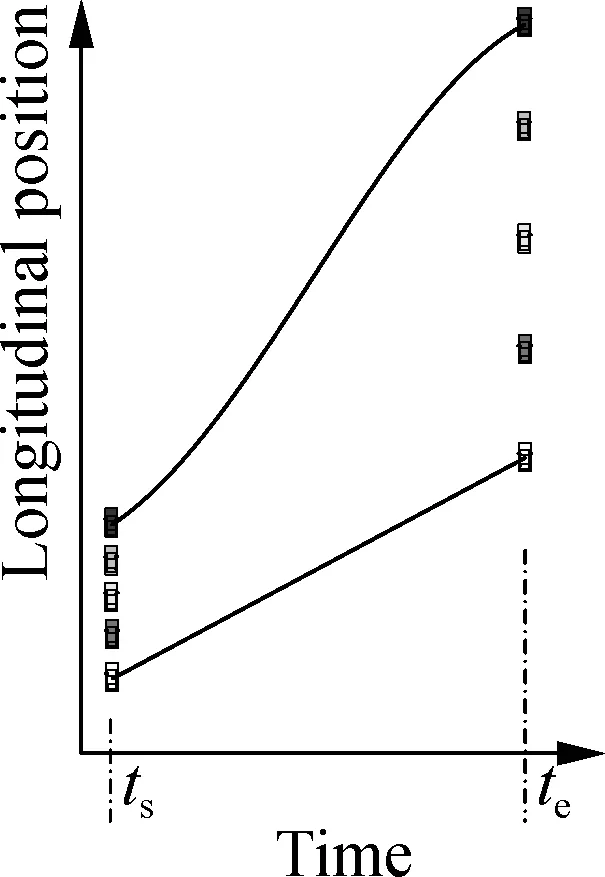
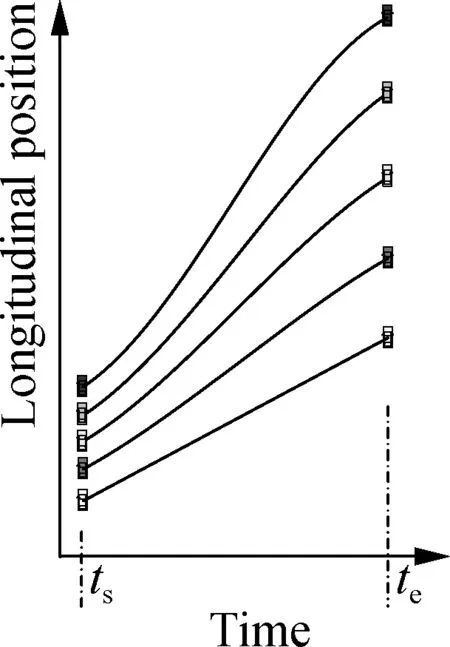
In the stage of uniform expending, the clearances of compact passing vehicles should be enlarged.Fig.4 shows the trajectory planning process in this stage. The problem of uniform expending is plotted in Fig.4(a). It is desired to widen the clearances between these vehicles, which can be achieved using two-step trajectory planning. The first step is to plan the trajectories of the last vehicle and the foremost vehicle to widen the distance between the two vehicles as indicated in Fig.4(b). The second step is to plan the trajectories of the vehicles between the foremost vehicle and the last vehicle according to their initial distances to the foremost vehicle and the last vehicle as demonstrated in Fig.4(c).
(a)
(b)
(c)
Fig.4Example of trajectory planning for uniform expending. (a) Problem; (b) The first step; (c) The second step>
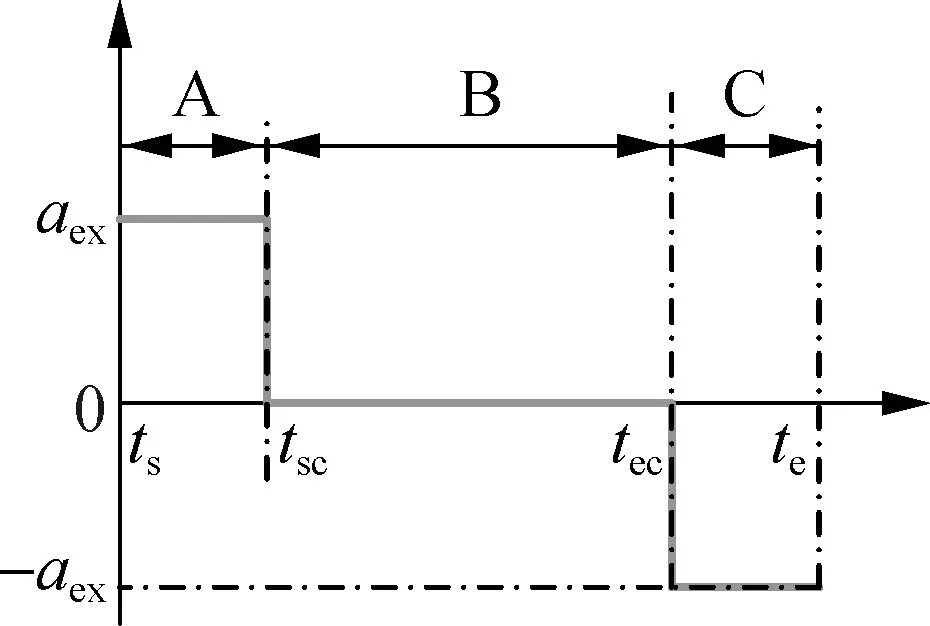
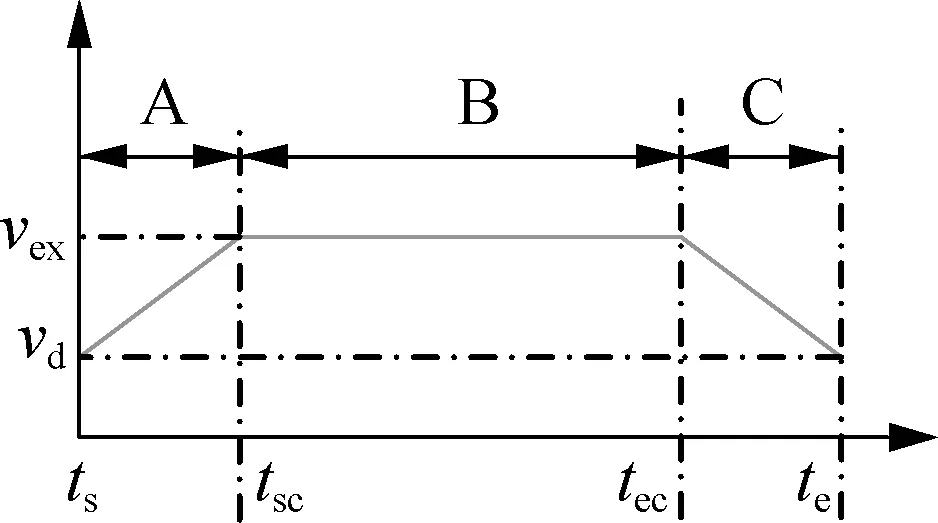
In the first step, the last compact passing vehicle has a constant speed and the trajectory of the foremost vehicle is planned to enlarge the distance between the two vehicles as shown in Fig.4(b). As indicated in Fig.5, to simplify the problem of trajectory planning of the foremost vehicle, the motion of the foremost vehicle is divided into three sections (sections A, B and C). In the first section, the acceleration of the vehicle isaex, which is a constant factor and lower than the maximum acceleration of the considered vehicles. In the second section, the acceleration of the vehicle is zero. The speed of the vehicle isvex, which is a constant factor and lower than the maximum speed of the considered vehicles. In the third section, the acceleration of the vehicle is -aexand the final speed isvdwhich is the desired speed of the vehicle. It can be found that, for most of the time in this stage, the speed of the foremost vehicle is higher than that of the last compact passing vehicle. Thus, the distance between the foremost vehicle and the last compact passing vehicle can be enlarged as shown in Fig.4(b).
(a)
(b)
The planned longitudinal acceleration,the speed and trajectory of the foremost vehicle in the three sections can be expressed as
(2)
(3)
(4)
wherea(t),v(t) ands(t) are the planned longitudinal acceleration, speed and trajectory, respectively;ssis the vehicle position in the beginning.tsc=ts+(vex-vd)/aex.tec=te-(vex-vd)/aex.ssc=ss+vd(tsc-ts)+0.5amax(tsc-ts)2is the position of the vehicle at the end of the first section.sec=ssc+vmax(tec-tsc) is the position of the vehicle at the end of the second section.
In the second step, the trajectories of the vehicles between the foremost vehicle and the last compact passing vehicle are planned. The planned trajectory of vehiclei, which is between the foremost vehicle and the last compact passing vehicle, can be expressed as
si(t)=sf,v(t)wi,f+sl,v(t)wi,l
(5)
wheresi(t) is the planned longitudinal trajectory of vehiclei.sf,v(t) andsl,v(t) are the longitudinal trajectory of the foremost vehicle and the last vehicle, respectively.wi,f=li,l/l,wi,l=li,f/l,l=li,f+li,l. Here,li,fandli,lare the initial distances of vehicleito the foremost vehicle and the last vehicle, respectively. Eq.(5) means that the ratio of the distances of vehicleito the foremost vehicle and the last vehicle is constant, which indicates that the trajectory of vehicleiis an interpolation of the trajectories of the foremost vehicle and the last vehicle. Since the distance of the foremost vehicle and the last vehicle is widened, the clearances of the vehicles between the foremost and last vehicles are also widened, as indicated in Fig.4(c).
2.4 Process of compact passing algorithm
Due to the limit of the length of a green period, the number of vehicles that can pass the stop line in a green period should be determined, which is critical for the application of the compact passing algorithm. If too many vehicles simultaneously start in a green period, some vehicles may fail to pass the intersection due to the length of a green period. Another critical point is that, after the stage of uniform expending, there should be sufficient clearance among vehicles. Thus, the number of compact passing vehicles should also be limited. The minimum clearance between vehicles after uniform expending is determined by the constant time-headway policy[20].
lmin=l0+kvd
(6)
wherelminis the minimum clearance after expending;kandl0are the factors to determine minimum clearance.
The number of compact passing vehicles can be determined by iterative trajectory planning based on the process shown in Fig.6. At the beginning of a green period, the count of compact passing vehicles is set to be one. There is only one vehicle, which is waiting just after the stop line, in the sequence of compact passing vehicles. Then, a vehicle after the vehicles in the sequence is added into the sequence. Next, the trajectories of the vehicles in the sequence are planned using the simultaneous starting algorithm. If all vehicles in the sequence cannot pass the intersection in a green period, the last added vehicle will be deleted in the sequence and the trajectories of other vehicles will be planned and output. If all vehicles in the sequence can pass the intersection in a green period, the vehicle trajectories in the second stage will be planned. Then, the clearances between vehicles after the second stage will be checked. If there are sufficient clearances after expanding, a vehicle will be added into the sequence and the process mentioned above will be repeated. If there are no sufficient clearances after expending, the last added vehicle will be deleted from the sequence and the trajectories of other vehicles in the sequence will be planned and outputted.
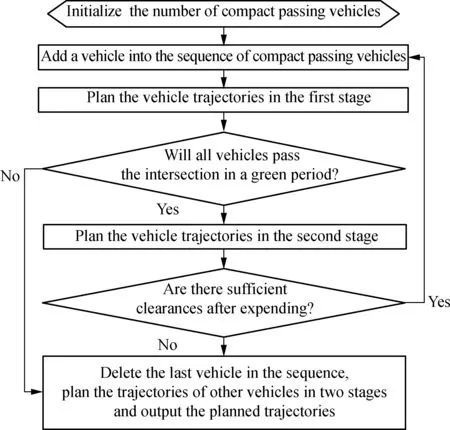
Fig.6 Flow chart of the compact passing algorithm
In summary,at the beginning of a green period, the compact passing algorithm is used by the IMU to coordinate the waiting vehicles to pass the intersection. In each lane, based on the compact passing algorithm, the IMU tries to add more vehicles into the sequence of compact passing vehicles. In a lane, when a vehicle that cannot be added into the sequence is found, the IMU stops adding vehicles and plans the trajectories of the vehicles in the sequence at the lane. The vehicles in the sequence will pass the intersection following the corresponding planned trajectories. The vehicles behind the sequence can follow the traffic signal and pass the intersection with normal wide clearances, which means that in a green period some vehicles pass the intersection with narrow clearances and some vehicles pass the intersection with normal wide clearances.
3 Numerical Simulations
To verify the effectiveness of the proposed algorithm, several simulations are demonstrated using MATLAB. Five intersection management methods (including two fixed-time methods, a vehicle actuated (VA) method[3]and the multi-agent (MA) method[13]) are considered. The two fixed-time traffic light methods have the green periods of 20 s and 30 s, which are represented by traffic light A (TLA) and traffic light B (TLB), respectively. The maximum and minimum green times of the VA method are 50 s and 15 s, respectively. Note that, the proposed compact passing (CP) algorithm can be used with TLA, TLB and VA, which are represented by TLA+CP, TLB+CP and VA+CP, respectively. The length of the straight lanes in the considered intersection is 750 m. The mean speed of the traffic flow is 10 m/s.
3.1 Simulation A
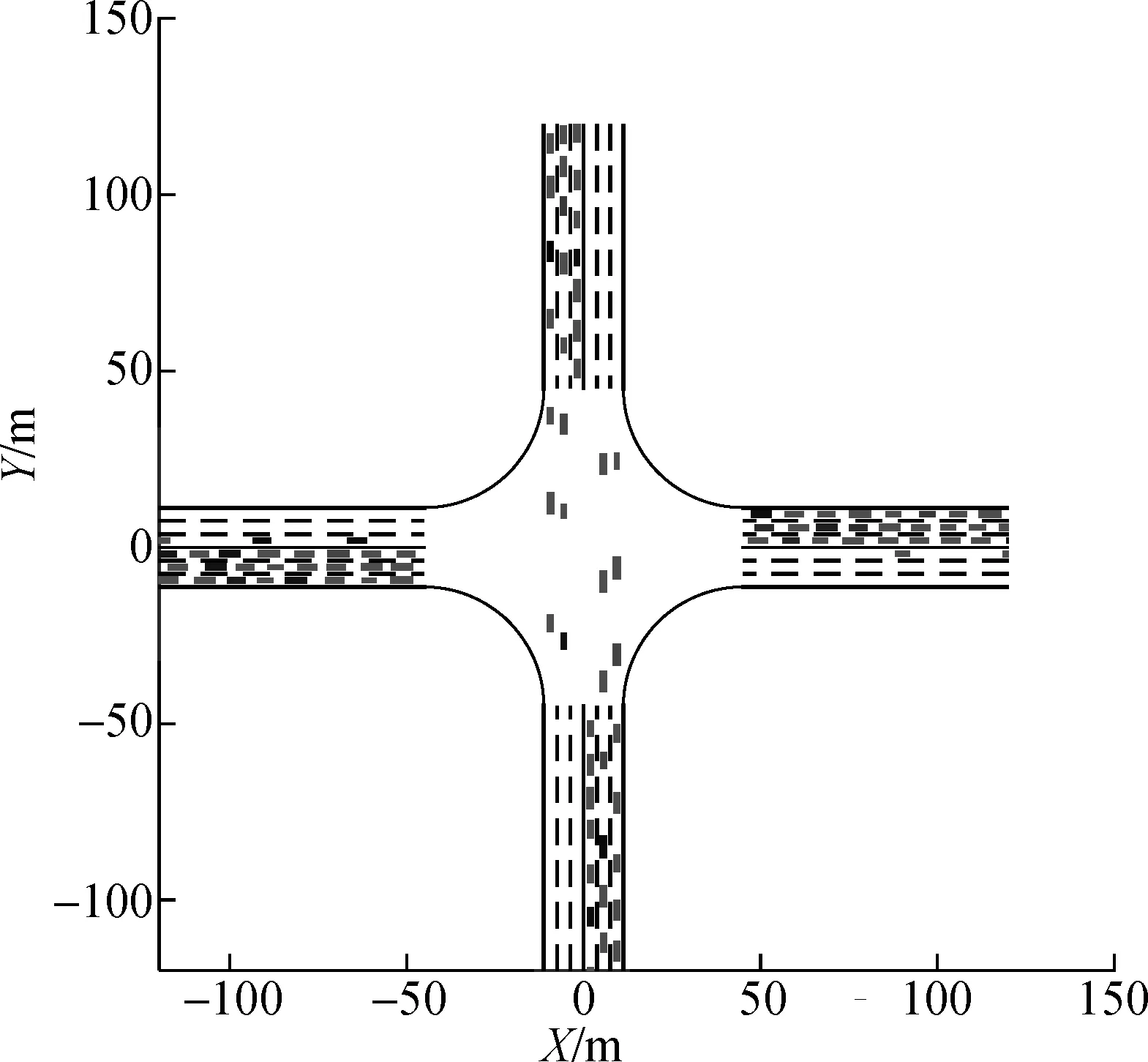
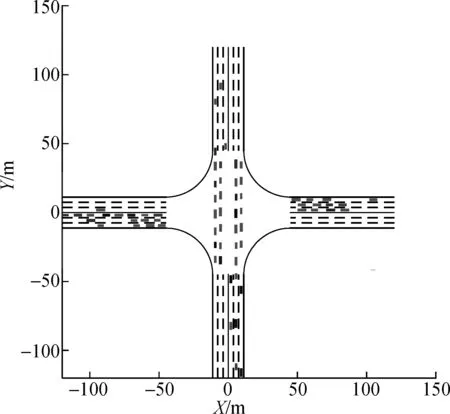
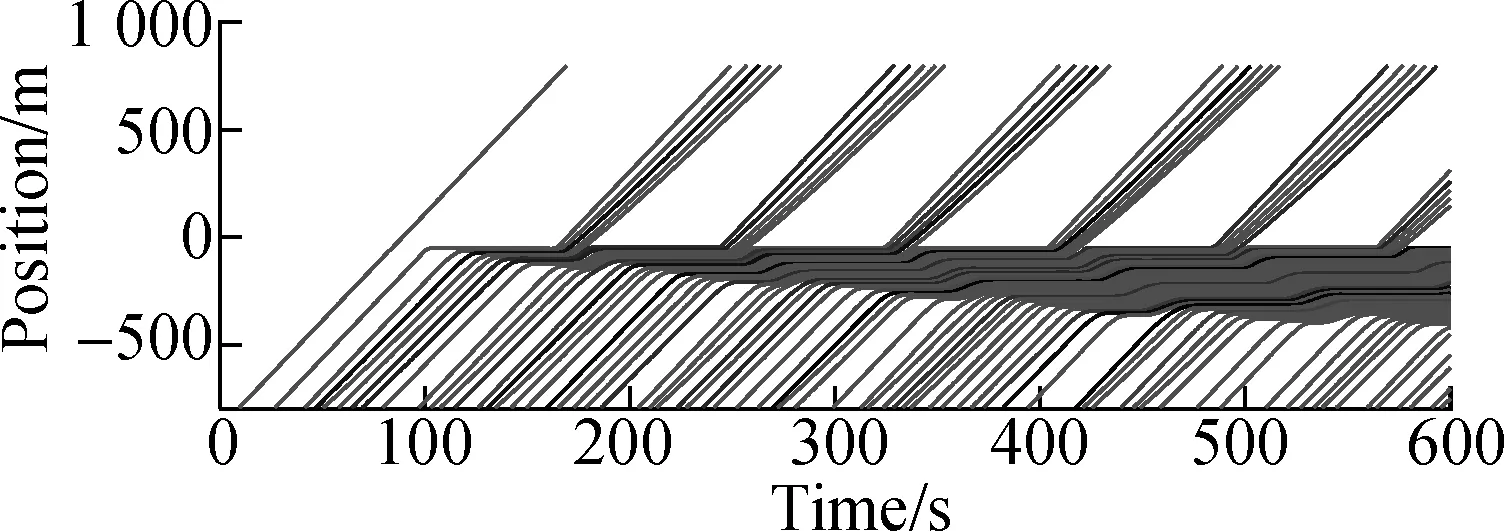
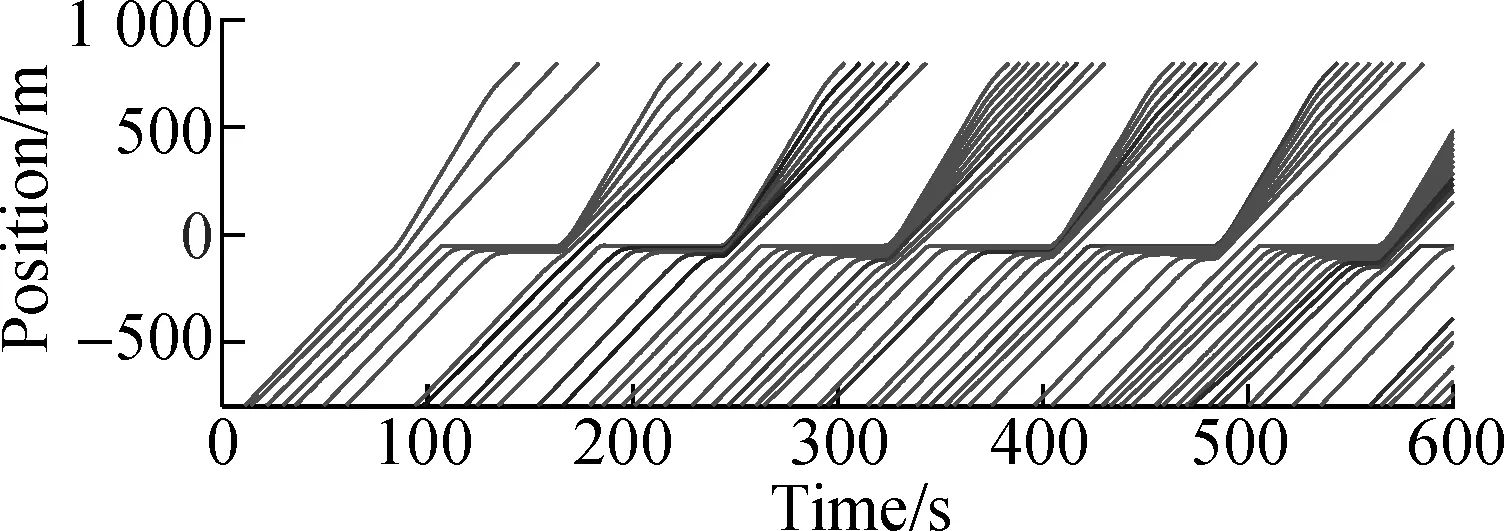
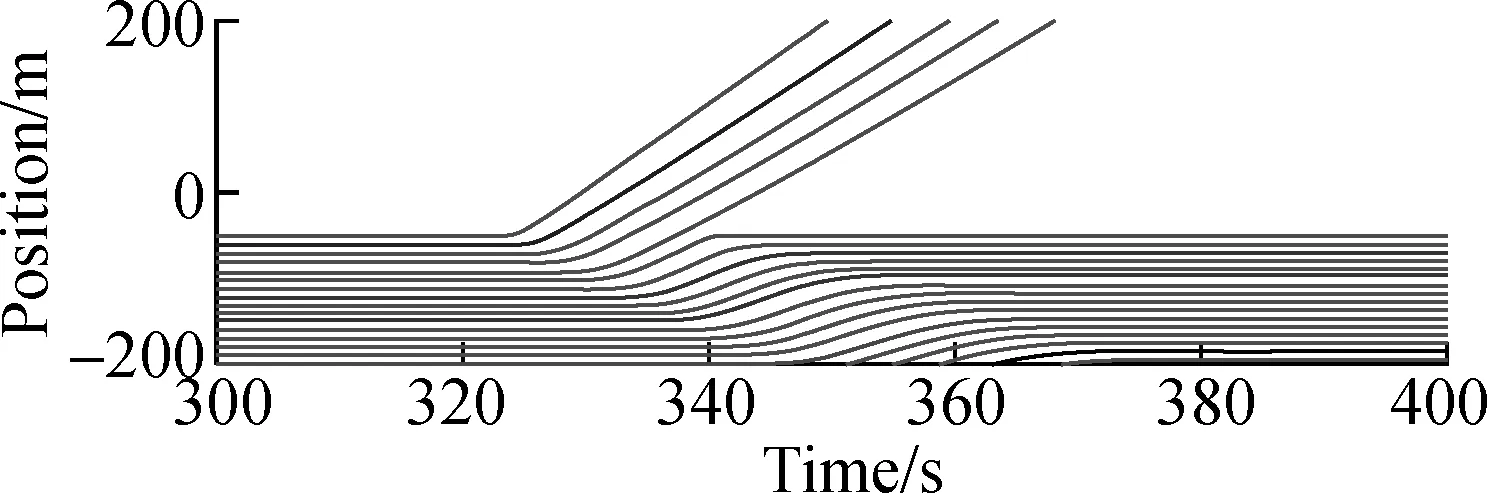
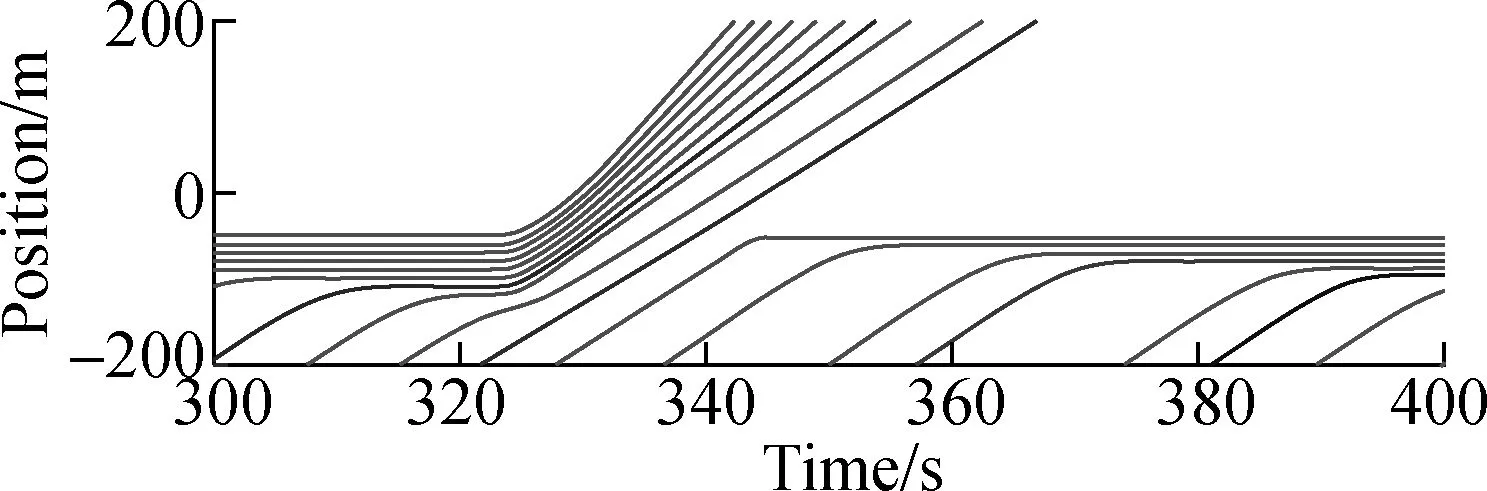
In this simulation, the details of the intersection controlled by TLA and TLA+CP are shown. The traffic load of each road is 1 200 veh/h. Two camera shots of the intersection controlled by TLA and TLA+CP are illustrated in Fig.7. The time-space diagrams of the vehicles in the left through lane of road S are shown and compared in Figs.8(a) and 8(b). Two local views of the time-space diagrams are further compared in Figs.8(c) and 8(d).
As indicated in Fig.8(a), for the intersection managed by TLA, there is a notable increase of the number of vehicles waiting in front of the intersection. By contrast, as shown in Fig.8(b), for the intersection managed by TLA+CP, there are few vehicles waiting before the intersection. Figs.8(c) and 8(d) indicate that, by TLA+CP, the clearances of vehicles are smaller than that of the TLA at the intersection. Thus, more vehicles can pass the intersection in a green period. After the intersection, the clearances of the vehicles managed by TLA+CP can be enlarged for normal driving. This simulation shows that, by the proposed method, more vehicles can pass the intersection in a green period. Note that, the simulations of other considered traffic lights methods, including TLB and VA, are much similar to that shown in this simulation. Thus, only the comparison of TLA is shown for simplification.
(a)
(b)
(a)
(b)
(c)
(d)
Fig.8Time-space diagrams of the vehicles in the left through lane at road S. (a) TLA; (b) TLA+CP; (c) Local view of TLA; (d) Local view of TLA+CP
3.2 Simulation B
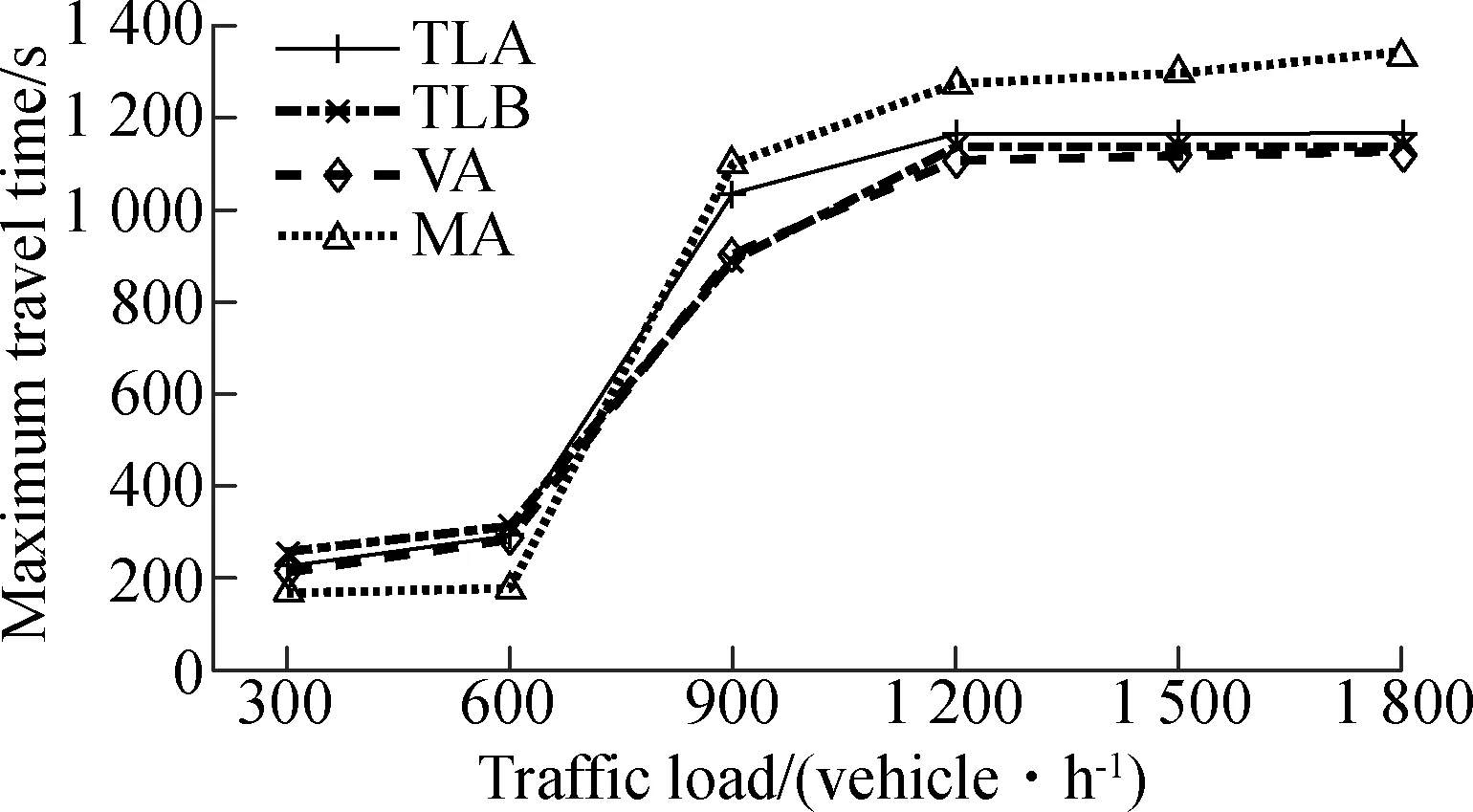
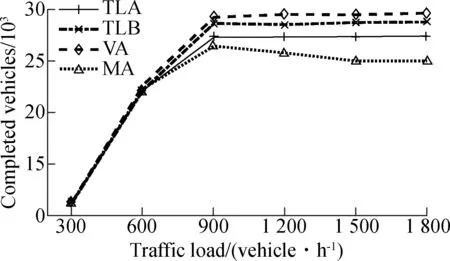
In this simulation, the performances of the TLA, TLB, VA and MA algorithms are compared under different traffic loads. The traffic loads of each road vary from 300 veh/h to 1 800 veh/h. The maximum travel time and the count of completed vehicles of TLA, TLB, VA and MA methods are shown in Fig.9, which indicate that under a low traffic load, the maximum travel time of the MA algorithm is less. This comparison indicates that the MA algorithm shows better performance than the traffic light methods under a low traffic load. However, under a high traffic load, the maximum travel time of the signal-based methods is shorter and there are more completed vehicles, which means that the signal-based methods show better performance than the MA methods under a high traffic load. The main reason is that, under a low traffic load, there are few conflicts of the trajectories of vehicles. It is more effective to manage the considered intersection according to individual vehicles. Under a high traffic load, there are more conflicts among the trajectories of vehicles. It is more effective to coordinate vehicles by flows.
(a)
(b)
This comparison shows that the new developed signal-free method is more suitable under a low traffic load. The signal-based methods still show benefits under a high traffic load. Thus, it is meaningful to further improve the performances of signal-based methods for signalized intersections.
3.3 Simulation C
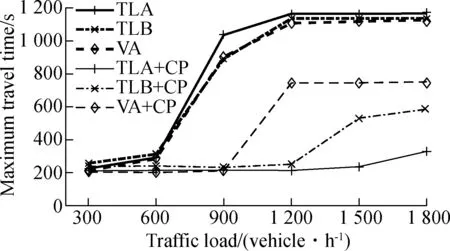
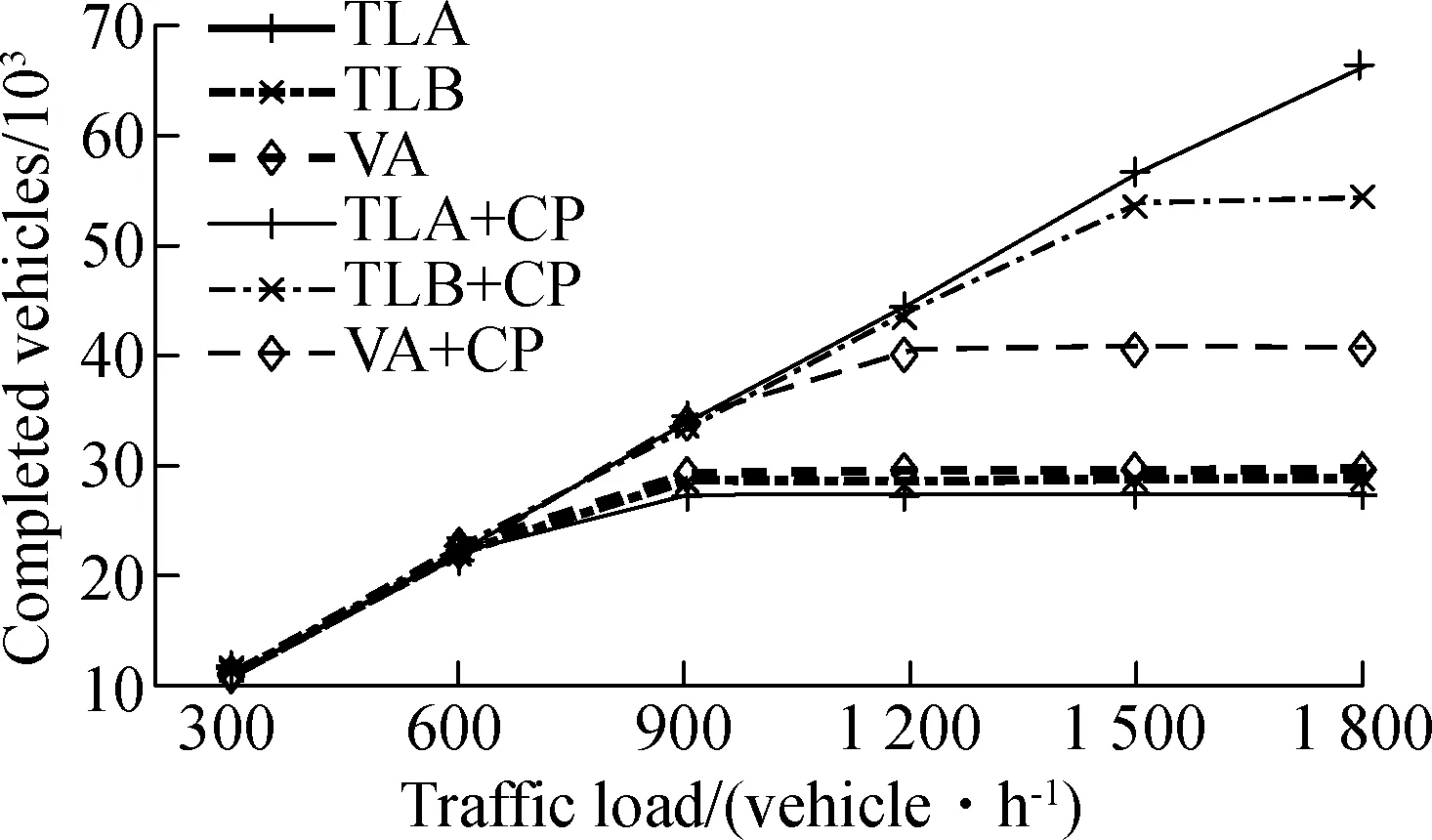
In this simulation, the effectiveness of the proposed compact passing algorithm for signal-based methods with different phase timing is demonstrated. The traffic load of each road varies from 300 veh/h to 1 800 veh/h. The performances of the signal-based algorithms with and without the proposed compact passing algorithm are compared in Fig.10.
(a)
(b)
It can be found from Figs.10(a) and 10(b) that, compared with the signal-based algorithms without compact passing, the maximum travel times of the signal-based algorithms with compact passing show much reduction, particularly under a high traffic load. More vehicles can pass the intersection based on the proposed compact passing algorithm. This is because, by using the proposed compact passing algorithm, more vehicles can pass the intersection with narrow clearances in a green period. Thus, the maximum travel time can be reduced and the completed vehicles can be increased. Furthermore, with the compact passing algorithm, TLA shows more improvement of performance than TLB. This is because, due to the limit of the count of compact passing vehicles in a green period, some vehicles may pass the intersection with a wide clearanc following the sequence of compact passing vehicles. Thus, if the green period is too long, more vehicles will pass the intersection with a wide clearance, which reduces the efficiency of the intersection. Moreover, VA shows the least improvement of performance compared with the fixed-time methods. This is because, in a green period, the length of the green period of VA is unknown, which is determined by passing vehicles. Thus, the compact passing vehicles can only be determined according to the minimum green period. The following vehicles will pass the intersection with normal wide clearances. In other words, for the VA method, the green period cannot be fully utilized for the compact passing algorithm. Thus, the improvement of the performance of the VA method is less than that of the fixed-time methods.
This simulation indicates that the proposed compact passing algorithm is effective for improving the performance of signal-based algorithms, which is essential for improving traffic efficiency and reducing the time cost on the road.
4 Conclusions
1) This paper investigates a compact passing algorithm for signalized intersection management. The main advantage of the proposed algorithm is that more vehicles can pass an intersection in a green period. Thus, the traffic efficiency of signalized intersections can be improved by the proposed algorithm.
2) The integrations of the compact passing algorithm with conventional fixed-time traffic light methods and vehicle actuated methods are made. The simulation results show that the proposed compact passing algorithm can greatly improve the performances of these signal-based algorithms.
3) In fact, since phase timing is not considered in the compact passing algorithm, the compact passing algorithm can also be applied to almost all the signal-based algorithms. Further studies will be made to extend the compact passing algorithm to other signal-based algorithms such as fuzzy logic control and adaptive control.
杂志排行
Journal of Southeast University(English Edition)的其它文章
- Influence of image data set noise on classification with a convolutional network
- A low-cost personal navigation unit
- Flexural behavior of steel reinforced engineered cementitious composite beams
- Analysis of conflict factors between pedestrians and right-turning vehicles at signalized intersections
- Effect of contract choice on upstream carbon emission reduction considering carbon taxation
- Multi-relaxation-time lattice Boltzmann simulation of slide damping in micro-scale shear-driven rarefied gas flow
