Multi-relaxation-time lattice Boltzmann simulation of slide damping in micro-scale shear-driven rarefied gas flow
2019-04-04SongXuchengLiPuZhuRui
Song Xucheng Li Pu Zhu Rui
(School of Mechanical Engineering, Southeast University, Nanjing 211189, China )
Abstract:To investigate the slide film damping in the micro-scale shear-driven rarefied gas flows, an effective multi-relaxation-time lattice Boltzmann method (MRT-LBM) is proposed. Through the Knudsen boundary layer model, the effects of wall and rarefaction are considered in the correction of relaxation time. The results of gas velocity distributions are compared among the MRT, Monte Carlo model (DSMC) and high-order LBM, and the effects of the tangential momentum accommodation coefficient on the gas velocity distributions are also compared between the MRT and the high-order LBM. It is indicated that the amendatory MRT-LBM can unlock the dilemma of simulation of micro-scale non-equilibrium. Finally, the effects of the Knudsen number, the Stokes number, and the gap between the plates on the damping are researched. The results show that by decreasing the Knudsen number or increasing the Stokes number, the slide film damping increases in the transition regime; however, as the size of the gap increases, the slide film damping decreases substantially.
Key words:lattice Boltzmann method; multi-relaxation-time; slide film damping; shear-driven oscillating flow
The modern technologies associated with microstructures such as micro-electro-mechanical systems, fuel cells and biochips have attracted significant interest recently and there is an urgent need for thorough research of physical phenomena and mechanisms of microstructures[1]. However, due to the complexities of the flow characteristics and the rarefaction effects in the transition and free-molecular-flow regimes, an accurate evaluation of the slide film damping in the micro-scale Couette plate flow is still a challenging issue. The rarefaction effects are described by the Knudsen numberKn, and the mean free path of moleculesλdivided by the feature lengthL. We will simulate the oscillating Couette flow in the transition flow regime.
The microscale flow has been studied in several works[2-3]. The corrected Reynolds equation is a common theoretical model applied to the micro-scale rarefied flow, which is commonly solved by a numerical approach, such as the Monte Carlo model (DSMC). Although the DSMC method has made great progress in simulating the rarefied gas flow with high Knudsen number, statistical noise will be generated when we evaluate the micro-scale flow damping at a low velocity, and thereby, the calculation costs are excessively high[4]. The molecular dynamics (MD) will be more suitable for the simulation of the liquid or dense gas flow; however, the application of the MD for simulating the rarefied gas flow and the micro-scale flow is not recommended due to the large amount of calculation and the slow convergence[5]. In the Lattice Boltzmann equation, the nonlinearity is imbedded in the left-hand side and the nonlinear advection is replaced by the linear streaming process. Therefore, it is different from macroscopic methods, which need to solve the Poisson equation at each time step to satisfy the continuous equation, and this fact greatly reduces the calculation time[6]. In addition, the collision and streaming processes are local, so the LBM method can be easily implemented in parallel computing, which further shortens the computational time.
Based on the mesoscopic scale, the precision of the lattice Boltzmann model (LBM), which can simulate the micro-scale flow and address these challenges, is compared to the DSMC or the direct solution methods. Furthermore, the LBM methodology has a good computational stability, and the boundary conditions can be easily handled, which is appropriate for parallel computing. The series of achievements have been acquired in simulating the microfluidic systems by employing LBM in the past few decades. The work by Nie at al.[7]is among the first ones that employed the LBM in simulating the microchannel flow as well as explaining the boundary slip velocity. However, the boundary adopted a nonslip bounce back scheme and the slip velocity was later confirmed as a discrete error[8]. Subsequently, Succi.[9]combined the rebound with the specular-reflection to characterize the slip velocities of the solid boundaries. After introducing the discrete diffuse boundary condition by Ansumali and Karlin[10], Tang et al.[11]established a general discrete form of the diffuse reflection. Meng et al.[12]systematically discussed the problems of the physical symmetry and the relaxation time selection in the gas micro-flow.
Owing to the inability of the standard LBM to capture the boundary Knudsen layer, some of its deficiencies have been revealed by conducting further research on the mechanics of the gas flow in the transition regimes. When the thin gas flows through the wall, a Knudsen layer that concerns the mean free path of moleculesλforms above the wall, in which the collision between the molecules is not sufficient and the molecule thermal equilibrium assumption would be no longer valid[13]. For solving these problems, the higher-order LBM was adopted by adding the higher-order equilibrium distribution function as well as the high precision Gauss-Hermite integral. However, introducing the high-order moment increases the complexity of the model, and the storage and computation costs increase, so some inherent advantages of the LBM will be limited. In this paper, a corrected effective relaxation time LBM is proposed, which takes into account the collision effect between the molecules and wall by introducing effective relaxation time. Furthermore, the MRT-LBM method can effectively reduce the problems of the increasing number of calculations and the storage produced by using the higher-order LBM method for simulating the gas flow in the transition regimes or a largeKn.
The above-mentioned literature mostly displays the simulations of the steady-state micro-scale flow; however, the engineering applications frequently involve the non-equilibrium gas flow such as micro-accelerometers, inertial sensors, resonant filters, and so on. As a result, a new numerical algorithm is required to evaluate the damping forces caused by the non-equilibrium effect of the gas flow. Tang et at.[14]employed a higher-order LBM to model the unsteady gas flow problems of the micro-scale single plate oscillation Couette flow. On this basis, we adopt the MRT-LBM to simulate the single plate periodic oscillating Couette flow on a micro-scale, and try to verify the correctness of the LBM in the analysis of the non-equilibrium micro-scale gas flow as well as the driven plate slide damping.
1 Micro-Scale Gas Flow LBM
1.1 MRT-LBM
In the momentum space, the collision operator can be expressed as
f(x+cΔt,t+Δt)-f(x,t)=-G-1S[g(x,t)-geq(x,t)]
(1)
whereg(x,t) andgeqare the vectors of moments;fis the velocity distribution function;Sis the relaxation matrix, andGis the transformation matrix.
The conversion between the speed and the moment space can be achieved by the following linear transformation:
g=Gf
(2)
f=G-1g
(3)
The discrete velocitiesckof D2Q9 is given by
(4)
whereais the lattice velocity and it is set to be 1 usually.
The matrixGfor D2Q9 is shown as

The moment vectorgis (ρ,w,ε,ix,tx,iy,ty,hxx,hxy)T, in whichρis the density, andixandiyare thexandycomponents of momentum.
(5)
(6)
Furthermore, the diagonal matrixSis
S=diag(0,0,1.4,0,s1,0,s1,s2,s2)
(7)
wheres1ands2are the relaxation times.
The macro variables, including the densityρ, the fluid velocity vectoru, and the pressurep, are stated by
(8)
(9)
(10)
1.2 Boundary condition
The relaxation times2associated withλin the MRT-LBM is given as[13]
(11)
whereHis the gap between the plates.
However, when the thin gas flows through the wall, a Knudsen layer forms above the wall and in the transition regimes. It implies that the Knudsen layer is an essential factor in studying the micro-scale rarefied Couette flow. Therefore,we introduce the effective relaxation time model proposed by Guo[15], as follows:
(12)
The modified functionΨis
Ζ(χ)=1+(χ-1)e-χ-χ2Tn(χ)
(13)
where

(14)
in whichTn(χ) is the exponential integral function.
At the boundary walls, the slip velocity has a significant influence on the velocity distribution between plates and therefore, we adopt the boundary conditions of BSR proposed by Succi[9]and the wall is located at 1/2 the lattice sites. The three unknown distribution functions at the upper boundary with known velocity are
f4=f2
(15)
whereuwis the upper plate velocity andris the tangential momentum accommodation coefficient. For achieving the above-mentioned second-order slide boundary condition, the tangential momentum accommodation coefficientrand the relaxation times1are given as
(16)
(17)
where
(18)
τq=s2-0.5
(19)
(20)
(21)
(22)
B=12+30τq(H)ζA1
(23)
2 Plate Oscillation Couette Flow
The upper surface atz=doscillates with velocityuoalong the horizontal direction, while the substrate has been fixed, as shown in Fig.1. Two control parameters of the Couette flow areKnand Stokes’ numberβ, where the latter represents the relative relationship between the unsteady and the viscous effects, defined by
(24)
whereυis the kinetic viscosity;ωis the oscillatory frequency. The characteristics of the structure are listed in Tab.1.

Fig.1 The slide film damping of the Couette flow model

Tab.1 Characteristics of the structure
In LBM simulations, the correlation parameters are dimensionless and the mapping between physical units and lattice units can be performed by dimensionless criterion numbers. The mapping is shown in Tab.2. Concerning the boundary conditions, the up and bottom adopt BSR and the left and right exploit periodic boundary conditions.

Tab.2 Dimensionless lattice units for plate oscillation Coquette flow
3 Simulation Results
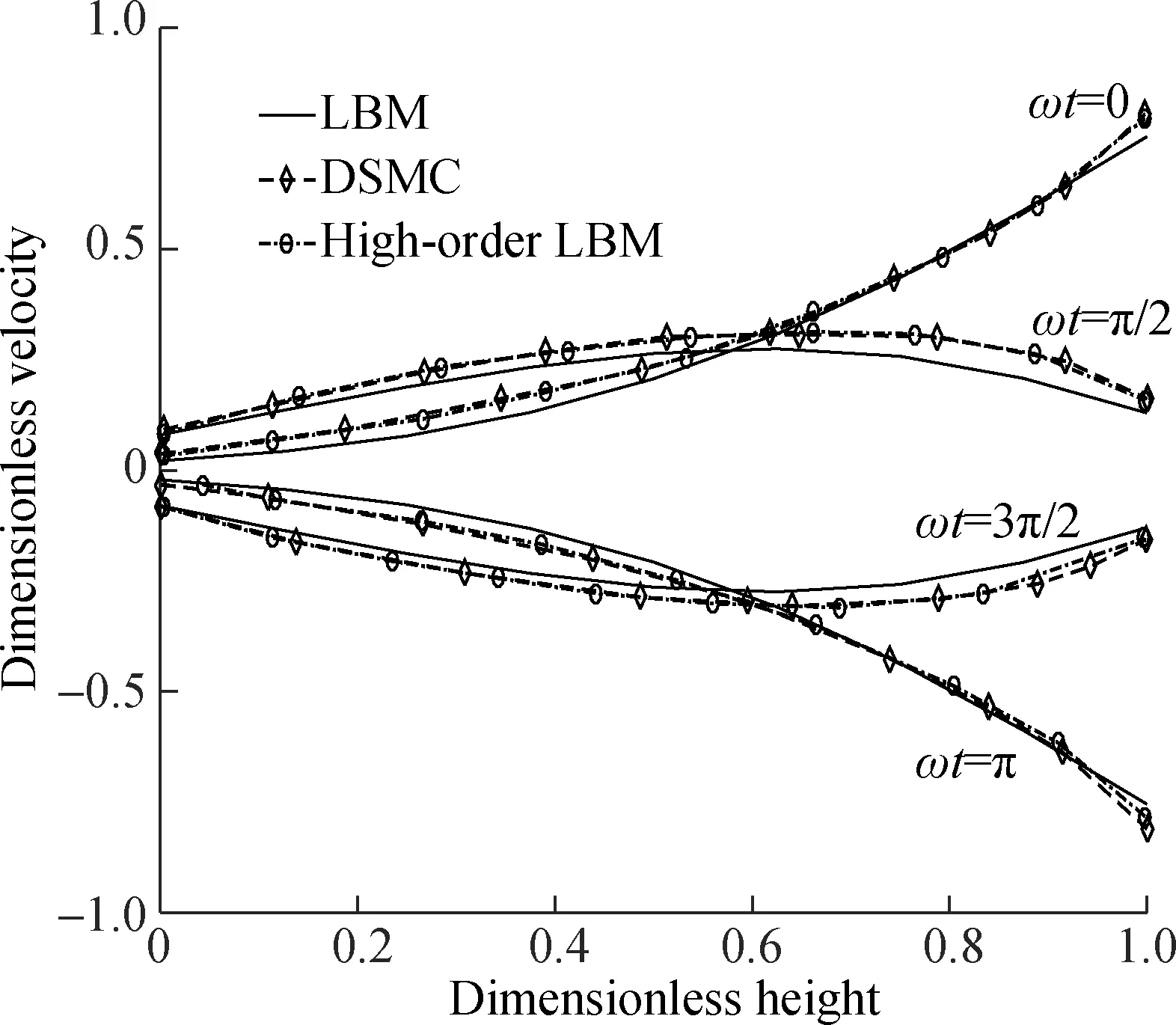
Fig.2 demonstrates the velocity profiles at the mid-section, normalized by the maximum velocity of the driven plate. The maximum relative errors between the results of the MRT-LBM and those of the DSMC are lower than 30.87%, 32.51%, 31.99%, respectively, in Figs.2(a), (b) and (c). The maximum relative errors between the MRT-LBM and the high-LBM are lower than 23.94%, 18.11%, 23.45% in Figs.2(a), (b) and (c).

(a)
(b)
(c)Fig.2 Velocity profiles at the mid-section.(a) Kn=0.1, β=4.0; (b) Kn=0.2 , β=2.0; (c) Kn=0.4, β=1.0
They indicate that the results acquired from the MRT-LBM are quite consistent with the DSMC data given by Hadjiconstantinou[16]as well as the high-LBM (D2Q13) data given by Tang et al[14].
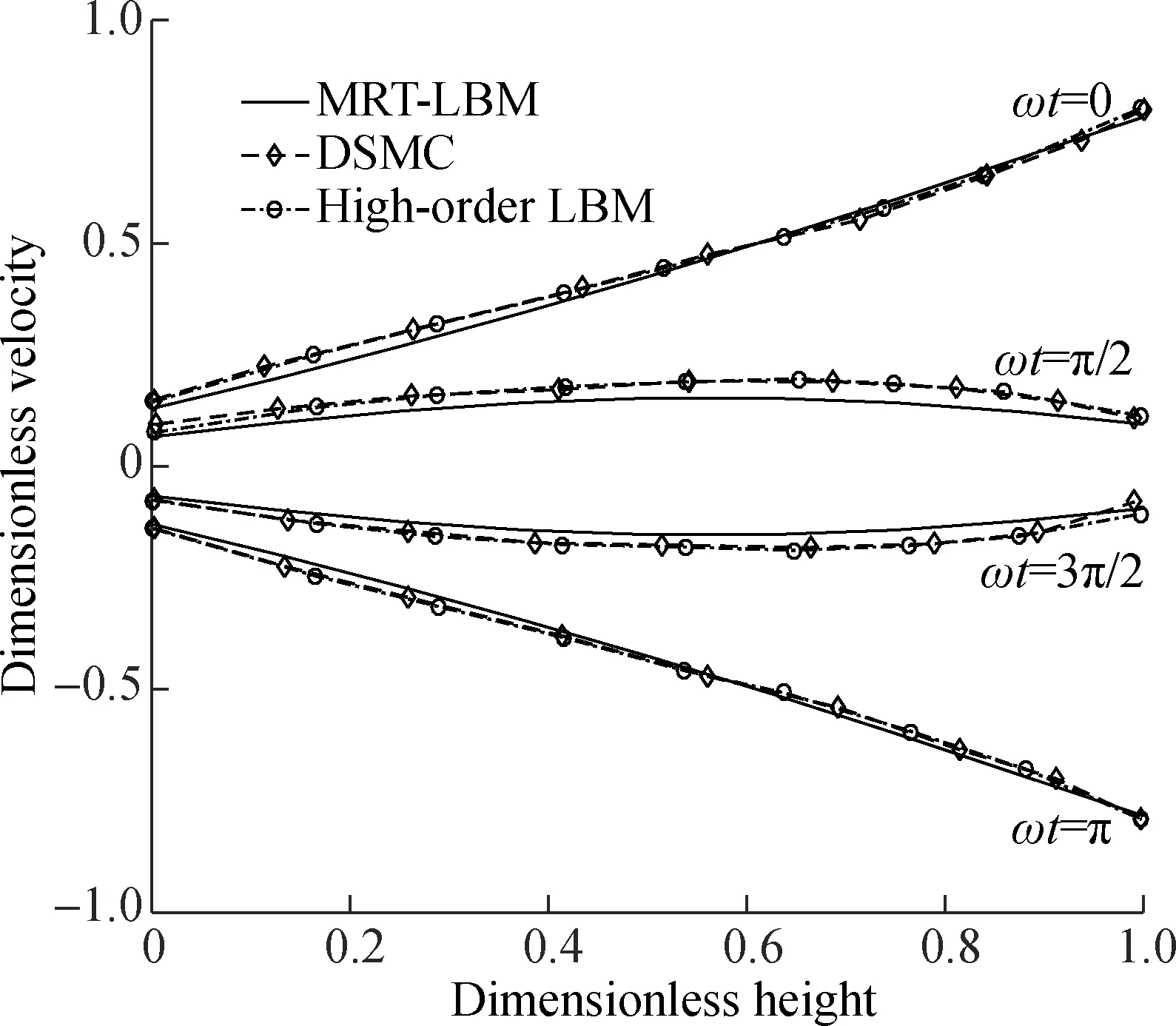
Fig.3 shows the velocity profiles of the mid-section (LX=25) at two moments during one cycle. The results of these profiles reveal that the slip velocity of the wall increases as the value ofrdecreases, which means that the slip film damping force is greater with a smaller value ofr. The results are in good agreement with the high-order LBM data by Tang et al[14].

Fig.3 Velocity profiles for Kn=0.1, β=4.0 revealing the effect of tangential momentum accommodation coefficient r
From the distribution function, the slide film damping can be evaluated directly. Therefore, it is convenient to compute the slide film damping and then compare it with that evaluated by the NS approaches. The predicted results of the slide film damping on the driven plate are shown in Fig.4, which are normalized by the maximum value of the damping. When the Knudsen number is close to 0.1, the slide film damping increases obviously with the increase of the Stoke number. As the Knudsen number increases, the slide film damping decreases at the fixed Stokes numbers. The obtained findings are in a good agreement with the DSMC data by Hadjiconstantinou[16].
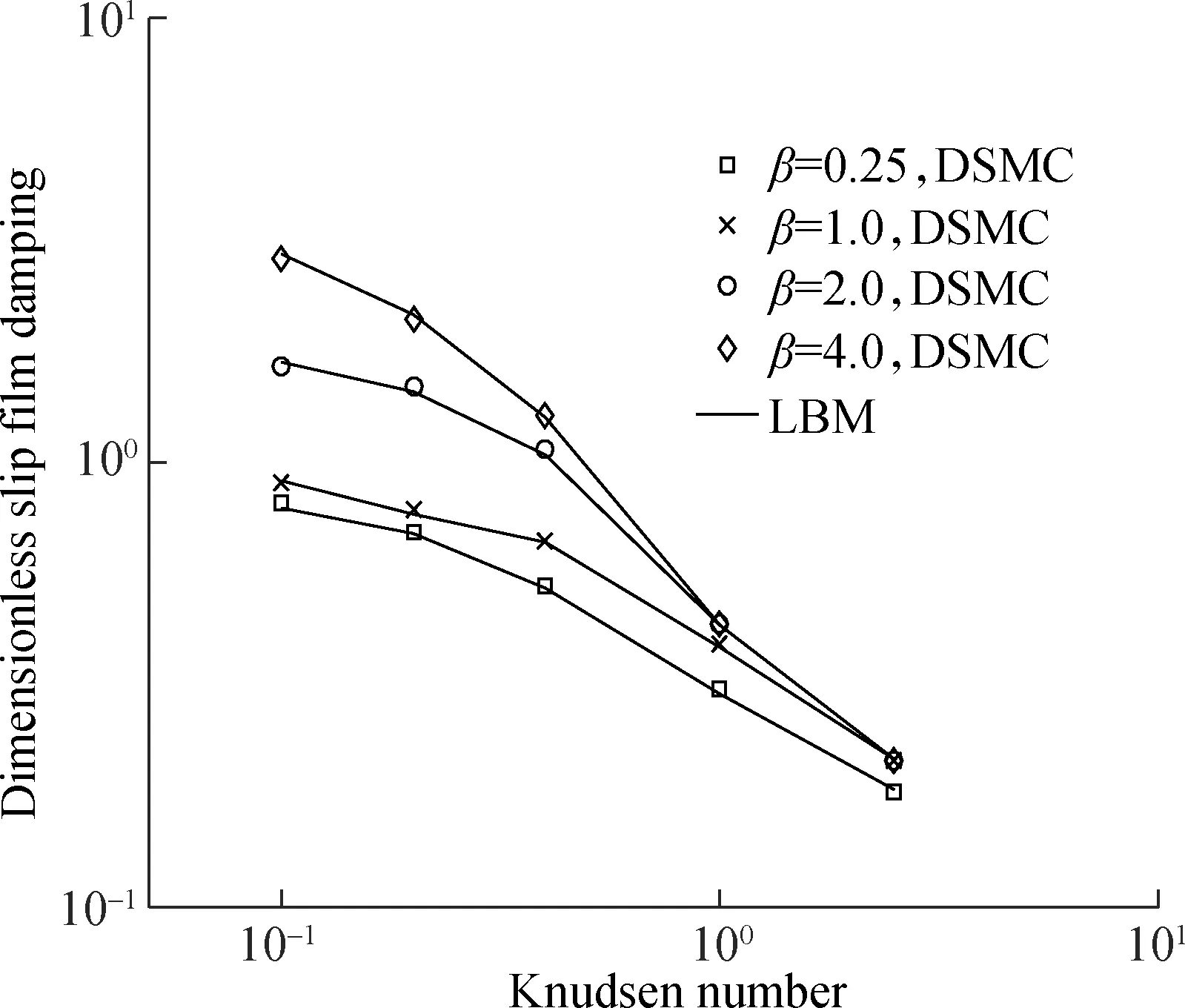
Fig.4 Slide film damping on the driven plate with the Knudsen number
From the studies which display the velocity and damping profiles in terms of the Knudsen number or the Stokes number, we conclude that the MRT-LBM is reliable for simulating the non-equilibrium micro-scale gas flow and the driven plate slide damping. Therefore, the relationship between the slip film damping and the plate gap is explored as shown in Fig.5. As the size of the gap increases, the slide film damping decreases obviously, so for the larger Knudsen numbers, the slide film damping is smaller.
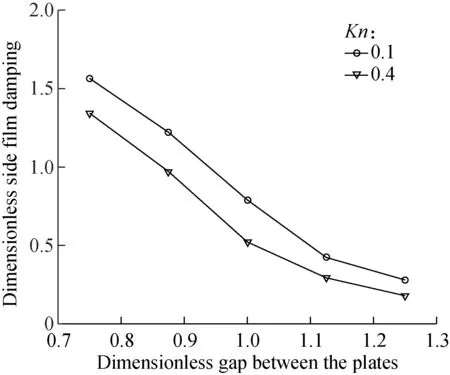
Fig.5 Slide film damping on the driven plate as a function of the gap between plates
4 Conclusions
1) An effective MRT-LBM approach was presented to investigate the slide film damping in laterally driven microstructures by taking into account the Knudsen layer. The velocity distributions between the driven plate and the substrate were examined, and the predicted results were in a good agreement with those of the DSMC.
2) The connections between the slide film damping on the driven plate and the Knudsen number, the Stokes number, and the gap between plates were investigated. The researchers found that slide film damping will increase, particularly in the transition regime, by decreasing the Knudsen number, size of gaps or increasing the Stokes number.
3) In contrast to the DSMC method, the proposed MRT-LBM gives a better slide film damping evaluation. Furthermore, the obtained results confirm the importance of considering the Knudsen layer in non-equilibrium flow simulations.
杂志排行
Journal of Southeast University(English Edition)的其它文章
- Influence of image data set noise on classification with a convolutional network
- A low-cost personal navigation unit
- Flexural behavior of steel reinforced engineered cementitious composite beams
- Compact passing algorithm for signalized intersection management based on vehicular network
- Analysis of conflict factors between pedestrians and right-turning vehicles at signalized intersections
- Effect of contract choice on upstream carbon emission reduction considering carbon taxation
