运用补体法巧解多面体外接球的相关问题

张桂华

(云南省红河州蒙自市第一高级中学 661199)

一、构造正方体

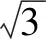
解析因为正三棱锥P-ABC中，PA,PB,PC两两互相垂直,所以可以把该正三棱锥补成一个正方体(如图), 正三棱锥P-ABC的外接球即为以PA,PB,PC为棱的正方体的外接球, 球心为正方体的中心，正方体的体对角线为正三棱锥外接球的直径.

点评该题若直接利用三棱锥来考虑不易入手，且难度较大.但若能注意到条件中的三条棱两两互相垂直,把正三棱锥补成一个正方体来考虑，利用正方体的体对角线为该正三棱锥外接球的直径，并找到球心是破解此题的关键.

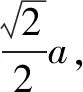
例2 如图，在等腰梯形ABCD中，AB=2DC=2,∠DAB=60°，E为AB的中点，将△ADE与△BEC分别沿ED、EC向上折起，使A、B重合于点P，则P-DCE三棱锥的外接球的体积为 ( ).

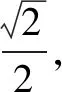
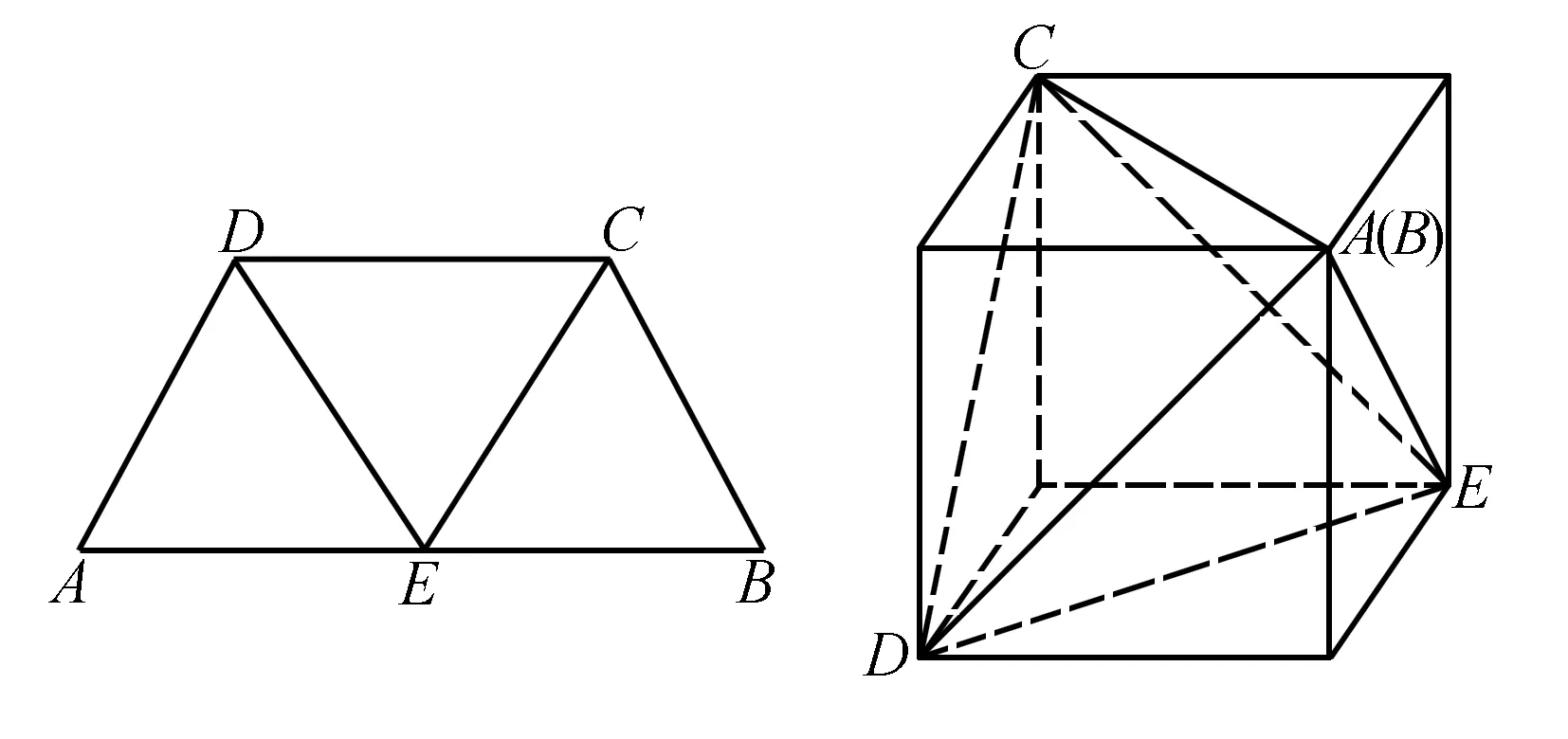
点评本题灵活性较强,不仅考查了组合体的位置关系、抽象概括能力、空间想象能力以及运算求解能力，还考查了转化思想，难度较大.若直接利用正四面体来考虑不易入手,但若能将正四面体补成一个正方体来考虑，则可极大地简化运算，能迅速求出三棱锥外接球的半径，从而使复杂问题迎刃而解.

点评该题若直接利用三棱锥来考虑很难入手.但若能注意到条件中的三个侧面两两互相垂直, 且侧棱长均相等，把此三棱锥补成一个正方体来考虑，利用正方体的体对角线为三棱锥外接球的直径是破解此题的关键.

二、构造长方体

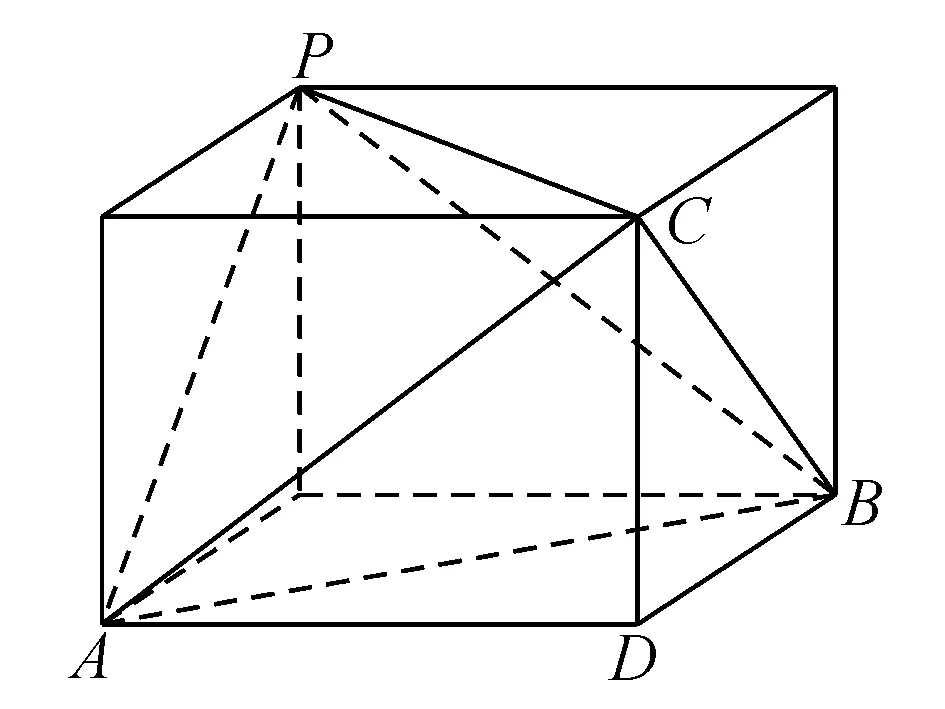
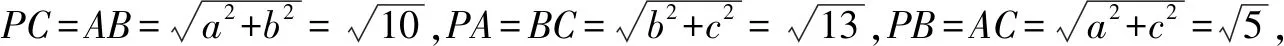
点评三棱锥的相对棱相等，探寻球心无从下手，但注意到长方体的面对角线相等，可将这个三棱锥补成一个长方体，利用长方体的体对角线就是该三棱锥的外接球的直径，从而巧妙求出外接球的半径.

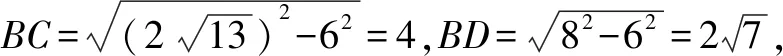
点评该题很难画出直观图，因此只能依赖空间想象，难度较大.但若能注意到条件中的三条棱两两互相垂直,可将这个三棱锥补成一个长方体，利用长方体的体对角线就是该三棱锥的外接球的直径，化繁为简，从而求出外接球的半径，是破解此题的关键.

总之，补体法是巧解多面体外接球的相关问题的常用方法.将多面体补成一个正方体或长方体，利用正(长)方体的体对角线为三棱锥外接球的直径是破解此类题的关键，可极大地简化运算，能迅速求出其外接球的半径.以下多面体可以补成正方形或长方体：

(1)三条侧棱两两互相垂直的正三棱锥；正四面体；四个面都是直角三角形的三棱锥，可分别将他们补成一个正方体；

(2)相对的棱相等的三棱锥、同一个顶点上的三条棱两两垂直的四面体都分别可补成一个长方体或正方体；

(3)三棱锥的三个侧面两两垂直，可将三棱锥补成一个长方体或正方体；

(4)若已知棱锥含有线面垂直关系，可将棱锥补成一个长方体或正方体.