学科素养导向下的2018全国卷数学试题回望

延宗殿

(山西省晋中市昔阳县中学校 045300)

一、重视基础，突出主干

数学考完后，教师普遍感到，今年高考数学试题全国卷在考查基础知识、基本技能和基本方法方面明显重于往年.试题全面考查基础，突出主干内容，强调通性通法，如集合、复数、函数、向量、算法、概率、三角函数、解三角形、线性规划、圆锥曲线等基础内容在选择填空题中都进行了有效的考查，这部分试题有利于稳定考生情绪；还有解答题对数列、统计、直线与圆锥曲线、立体几何、函数与导数等高中数学主干内容也进行了重点的考查，充分体现了试卷对数学知识考查的基础性、全面性和综合性.另外试卷也非常注重通性通法的考查.

表1 全国2卷理科数学选择填空题考点统计表

全国2卷理数的第17题考查了等差数列最基础的知识，难度很低.这体现了命题人对基础知识和基本方法的重视.要求考生对这些基础内容必须熟练掌握.

二、稳定求新，不落俗套

每年高考试题都在追求稳定中求创新，今年全国卷试题也不例外.同时试题也追求题型设计的创新.如第8题以哥德巴赫猜想为背景，巧妙地设计了一道古典概率计算问题.第18题考查了线性回归模型的具体应用和相关系数的内容，要求学生根据折线图和相关系数的大小做出判断，出题角度非常新颖.

再如解答题中解析几何放在了立体几何前面进行考查，与往年比较，降低了解析几何解答题的难度.一般解析几何解答题都在20题的位置，无论平时的考试还是高考，大多数考生对于这道题的第2问都选择放弃.今年考题将解析几何解答提前一个位置，由一道难题变成了一道中档题，这样考生应该努力进行解答，就不能再选择“放弃”了.对高中教学起到了很好的导向作用.本题考验学生的随机应变与心理素质，本题源于教材，以抛物线中过焦点的弦为直径的圆和准线相切为背景，设问方式新颖，不落俗套.

例1 (2018全国2理17)记Sn为等差数列(an)的前n项和，已知a1=-7，S3=-15.

(1)求{an}的通项公式；

(2)求Sn，并求Sn的最小值.

解析(1)设{an}的公差为d，由题意得3a1+3d=-15.

由a1=-7得d=2.

所以{an}的通项公式为an=2n-9.

(2)由(1)得Sn=n2-8n=(n-4)2-16.

所以当n=4时,Sn取得最小值,最小值为-16.

例2 设抛物线C：y2=4x的焦点为F，过F且斜率为k(k>0)的直线l与C交于A，B两点，|AB|=8．

(1)求l的方程；

(2)求过点A，B且与C的准线相切的圆的方程．

解析(1)由题意得F(1,0)，l的方程为y=k(x-1)(k>0).设A(x1,y1),B(x2,y2)，

因此l的方程为y=x-1.

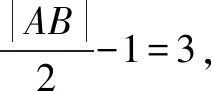
所求圆的方程为(x-3)2+(y-2)2=16.

问题：以AB为直径的圆恒与抛物线C的准线相切，反之过点A，B且与C准线l相切的圆是否一定以AB为直径？

显然，圆心M一定在AB的垂直平分线上，且到A(B)的距离和到曲线C的准线的距离相等.根据抛物线的定义知，点M在以A(B)为焦点以直线l为准线的抛物线上E上，即M为AB的垂直平分线与曲线E的交点(如图所示)AB的垂直平分线方程为y-2=-(x-3)，即y=-x+5.

设所求圆的圆心坐标为(x0,y0)，则

因此所求圆除了一个以AB为直径外，另一个圆的圆心为(11，-6)，其方程为(x-11)2+(y+6)2=144.

文理第16题以圆锥为载体考查了空间几何体的线线角、线面角和面积、体积计算.这样的命题在上个世纪90年代考过，近十年来考查旋转体通常以球和多面体组合体为载体进行考查.

立体几何解答题对几何证明提出了较高的要求，由于高考考试大纲删除了选修4-1.几何证明选讲,所以对逻辑推理,特别是利用公理法进行推理的能力的考查就落在立体几何和解析几何题上.从第20题第(1)问的线面垂直的证明看,其难度明显高于往年线面关系的证明.高考命题的这个变化,应该对今后的高中教学中有启示作用.

三、加强数学核心素养的考查

今年全国理科卷试题对数学核心素养有更深入的考查.如第3题对于学生的逻辑推理与直观想象提出了较高的要求；第18题充分考查学生的数据分析和数学建模能力；第20题考查考生的空间想象、逻辑推理和数学运算能力；第19题以抛物线过焦点的弦为载体，考查学生的运算求解和逻辑推理能力；全国文理卷第21题为姊妹题设计，理科数学是以指数函数和对数函数为载体，文科数学以多项式函数为载体考查了用导数研究函数的基本方法，主要考查了求函数的单调区间、函数的极值、函数的零点等基本问题.对学生数学抽象与数学思维品质都有很高的要求，充分考查学生分析问题和解决问题的能力.

例3 (2018全国2理19)已知函数f(x)=ex-ax2．

(1)若a=1，证明：当x≥0时，f(x)≥1；

(2)若f(x)在(0,+∞)只有一个零点，求a．

解析(1)当a=1时，f(x)≥1等价于(x2+1)e-x-1≤0．

设函数g(x)=(x2+1)e-x-1，则g′(x)=-(x2-2x+1)e-x=-(x-1)2e-x．

当x≠1时，g′(x)<0，所以g(x)在(0,+∞)单调递减．

而g(0)=0，故当x≥0时，g(x)≤0，即f(x)≥1．

(2)设函数h(x)=1-ax2e-x．

f(x)在(0,+∞)只有一个零点当且仅当h(x)在(0,+∞)只有一个零点．

(ⅰ)当a≤0时，h(x)>0，h(x)没有零点；

(ⅱ)当a>0时，h′(x)=ax(x-2)e-x．

当x∈(0,2)时，h′(x)<0；当x∈(2,+∞)时，h′(x)>0．

所以h(x)在(0,2)单调递减，在(2,+∞)单调递增．

故h(x)在(2,4a)有一个零点，因此h(x)在(0,+∞)有两个零点．

四、几点启示

今年的高考数学试卷，对备考2019年高考的学生，有以下几点启发：

1．必须重视“四基”

高考对基础知识、基本技能、基本方法和基本数学体验的要求越来越高，因此我们要在复习备考的过程中，结合教材和考纲，熟练掌握高中数学的基础知识和解题的通法，不宜好高骛远，花费太多的时间去钻研偏难怪题.

2．必须深入研究历年高考真题

在打好基础的前提下，认真研究历年高考真题，掌握高考命题的一般规律，对提高复习的效率有很大的帮助.

3．利用典型例题提高解题水平

应该通过学习研究一类题目的解法中，掌握核心的数学思想和数学方法，开拓我们的解题思路，提高解题水平.这是培养学生的数学核心素养所必须.

一般来说，一道题目能够成为典型例题，它必须具备以下几条要素：重点与热点；入口较宽，解法多样(至少两种解法)；解法能够迁移；变式与推广.难度中等.

从上个年度的备考情况看，多数教师对题的研究不够充分，表现在，一是解法单调.如果你只能用一种方法解决这道题，那么这道题就不能作为例题，原因很简单，主要是你对这道题还没有融会贯通，还不能多角度来认识它，也就是你对它理解的还不透彻，还不能灵活变通.这样的题怎么能作为例题呢.二是难度太大，一道题目如果难度太大，那么课堂上大多数学生往往听不懂，教师也讲不清楚；选题应该立足中档试题，难度系数在0.5-0.65范围内比较合适.中档综合题区分度好，训练价值高，教师讲得清楚，学生听得明白，有利于学生数学素养的提高；三是就题论题，不回顾、不反思、不总结.常见的是，一些教师讲解完一个题目后，马上转入下一个问题的解决，他们不对这道题目的解题步骤进行回顾与反思. 如解题中用到了哪些知识？哪些方法？这些知识和方法是怎样联系起来的？自己是怎么想到它们的？

困难在哪里？关键是什么？遇到过什么障碍？后来是怎么解决的？

是否还有别的解决方法?命题能够推广吗？

条件能减弱吗？结论能加强吗？这些方法体现了什么样的数学思想？

充分发挥典型例题的作用，提高教学效果，减轻学生负担，分析典型例题的解题过程是提高学生解题能力的有效途径.

结尾：2018年全国卷数学试题大气、大道，题干简洁明了，解答严谨规范.

试题取材源于生活考查的终极目标服务于学生未来的可持续发展，能力立意，素养导航，打造数学高考考试新形态.

给2019届考生的建议：立足基础，注重数学的本质，掌握数学的思想方法.真正把高中数学每个知识点理解透彻，在学习过程中善于用数学思维去分析问题和解决问题，只有这样才能真正地掌握数学，才能在最终的高考中取得满意的成绩.