基于变换声学的角反射器的设计∗

毕亚峰1,2 贾 晗1,2†杨 军1,2

(1中国科学院噪声与振动重点实验室(声学研究所) 北京 100190)

(2中国科学院大学 北京 100049)

0 引言

后向反射器，是一种能将入射波按照入射方向进行反射的器件。由于它可以显著地增加散射截面和回波强度，所以有着广泛的应用。通常情况下，后向反射器表现为角反射器[1−3]的形式，通过两个互相垂直的反射面将入射声(电磁)波多次反射，最终实现出射声(电磁)波的反向传播。然而由于体积和形状的限制，很多情况下角反射器难以实用，往往需要平面或者较为扁平的几何结构去实现类似的反射效果，而变换声学[4−8]则为此提供了可能。变换声学将空间坐标的变换与器件的材料属性两者关联起来，从而可以设计出许多新型声学器件，如隐身衣[9−12]、声学弯管[13−15]、透镜等等[16−18]。利用变换理论设计的反射器也已出现[19−23]，但是这些器件大多参数极端，不均匀而且各向异性，因此难以实现。本文提出一种基于线性坐标映射的反射器，在这种映射下，反射器的参数变得均匀，仅仅需要各向异性的超材料即可实现。结合Biot流体理论[24]，这种反射器可以由周期层状流体构成。有限元仿真结果证明了该结构的有效性，对于不同频率的声波，该反射器也具有较好的性能。这种基于变换声学的反射体更具有实用性，为超材料的具体应用带来了可能。

1 映射关系与变换声学

二维的声反射器的映射关系如图1所示。图1(a)中，y=0界面为硬地面，在地面上放置蓝色三角形的反射器。根据角反射器的原理[1−3]，两个互相垂直的反射面，在45◦范围内可以将入射波按照原方向反射，因此，在图1(b)中v<0的区域需要构建出一个直角空间，并将红色虚线设置为反射边界。声波在该空间中的传播如黄色箭头所示，入射波将被反射回相应的方向。声反射器实物所处的空间为图1(a)，称为实空间；它所表现出的声学性质应该与图1(b)所示的空间一致，因此图1(b)所处的空间称为虚空间。

利用以下数学关系，可以将实空间与虚空间中的蓝色区域进行相互映射：

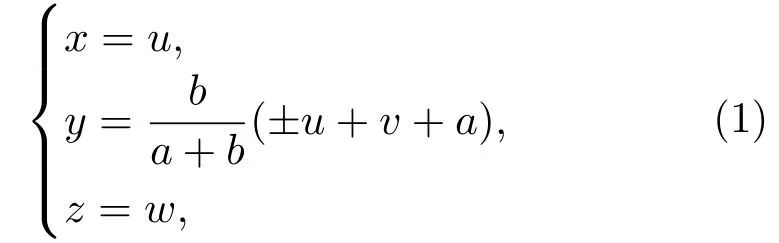
其中，±分别对应u<0与u>0的情况。在该映射下，虚空间(u,v,w)中蓝色的四边形区域被压缩至实空间中(x,y,z)的蓝色三角形区域。红色虚线边界则对应到实空间中的x轴。该映射的雅克比矩阵A为

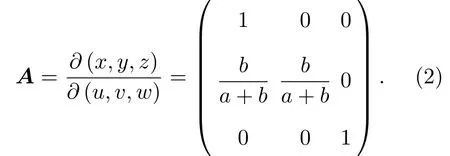
根据变换声学理论[8]，反射器的密度和模量为

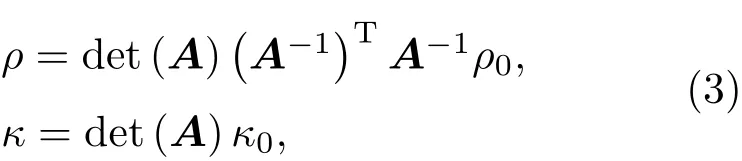
其中，ρ0和κ0分别为背景流体的密度和模量。将公式(2)中的雅克比矩阵A带入，可得

该密度矩阵与模量即为实现声反射器所需的参数。

图1 声反射器的空间映射关系Fig.1 The mapping rules of the acoustical retrodirective ref l ector

2 单元与反射器模型

为了更清晰地说明声反射器的设计过程，此处将其几何参数设定为a=160 cm，b=20 cm。该反射器为一个放置于地面上的钝角三角形，空气的密度和模量分别为ρ0=1.21 kg/m3和κ0=142.36 kPa。根据前文所述的变换声学方法，可以求得其密度矩阵和模量为

可见，此时密度矩阵存在非对角项，这是因为在变换声学的计算过程中，选取的是笛卡尔坐标系，该坐标系与密度矩阵的主轴方向存在一定的夹角，所以在矩阵中出现了非对角分量。因此，需要将密度矩阵进行旋转α=6.42◦，从而将其中的非对角项消除[9]，得到密度矩阵的特征值：

此时，可以得到密度矩阵的主轴坐标系：将x-y坐标系逆时针旋转α=6.42◦后所得到的x′-y′坐标系，如图2(a)所示。由求出的密度矩阵可知，在声反射器中，各个方向表现出的密度并不一样，所以需要各向异性密度的流体进行实现。然而在自然界中并不存在天然各向异性的流体，因此需要引入人工周期介质，Biot流体理论[6,24]则为此提供了可能。假设有两种不同的各向同性的流体介质(A和B)，其密度和模量分别为ρA，ρB和κA，κB。在两种介质分层厚度d相等的情况下，将其周期交错排列(图2(b))，于是在长波极限条件下可以得到该结构的等效参数：

图2 反射器结构Fig.2 The model of the acoustical retrodirective ref l ector

对于公式(6)中的介质而言，利用分层流体可以在长波极限下获得等效的各向异性密度。假设每层厚度d=0.5 mm，则单元大小L=1 mm。结合公式(6)和公式(7)，计算可得ρA=21.99 kg/m3，ρB=0.07 kg/m3和κA=2.62 MPa，κB=7.93 kPa。将流体A与流体B周期交错排列形成单元，并利用参数检索法[25]得到它的等效参数，以验证设计的单元的有效性。检索结果如图3所示，图3(a)为厚度L=1 mm的单元等效密度随频率变化图，其中方块和圆点标志为单元所体现出的密度，直线为器件设计所需的密度。可见在100 Hz∼4000 Hz范围内，单元两个方向的密度随频率改变很小，而且与设计所需的密度相吻合。两个方向上密度的巨大差别也体现出了该单元密度各向异性的特点。图3(b)为单元等效模量随频率变化图，同样的，方块和圆点为单元表现出的模量，而直线为器件设计所需模量。图3(b)中，低频情况下两个方向上的模量几乎完全一致，随着频率增加，模量值逐渐有所偏差，一直到4000 Hz时，两个方向上的模量相差达到10%。整体而言，两个方向上的模量与器件所需模量吻合，因此该单元具有密度各向异性，模量各向同性的特点。

图3 单元参数随频率变化Fig.3 Ef f ective parameters of the unit cell from 100 Hz to 4000 Hz

该单元的稳定性也能从它的能带曲线中体现出来。对于文中所述的厚度为1 mm、两种介质周期分层的单元，图4给出了它的能带曲线。图4中，横坐标为波矢k，波矢垂直于分层方向(图2(b)中的y′方向)，纵坐标为频率f。黑色点线为单元的能带曲线，而红色虚线为沿y′方向理论上设计所需要的声速。在能带曲线中，相速度cp=2πf/k，所以黑色点线的斜率与单元声速直接相关，而且斜率的稳定性也可以反映出单元的工作带宽。在图4中，频率低于4 kHz时，黑色点线与红色虚线几乎完全重合，因此在这段频率范围内，该单元都可以稳定有效地工作。此时声波波长远大于单元的尺寸，两种流体被视为一个整体做运动，所以在低频条件下，单元会体现出稳定的特性。随着频率的增加，黑色点线逐渐偏离红色虚线，单元参数不再稳定，这时单元内声波波长与流体的层厚越来越接近，两种流体不能再被视为一个整体，所以频率高于4 kHz后单元开始慢慢失效。

综上所述，该单元的参数在较宽频率范围内且与设计的参数相吻合，因此可以进一步利用其构建超材料声反射器。

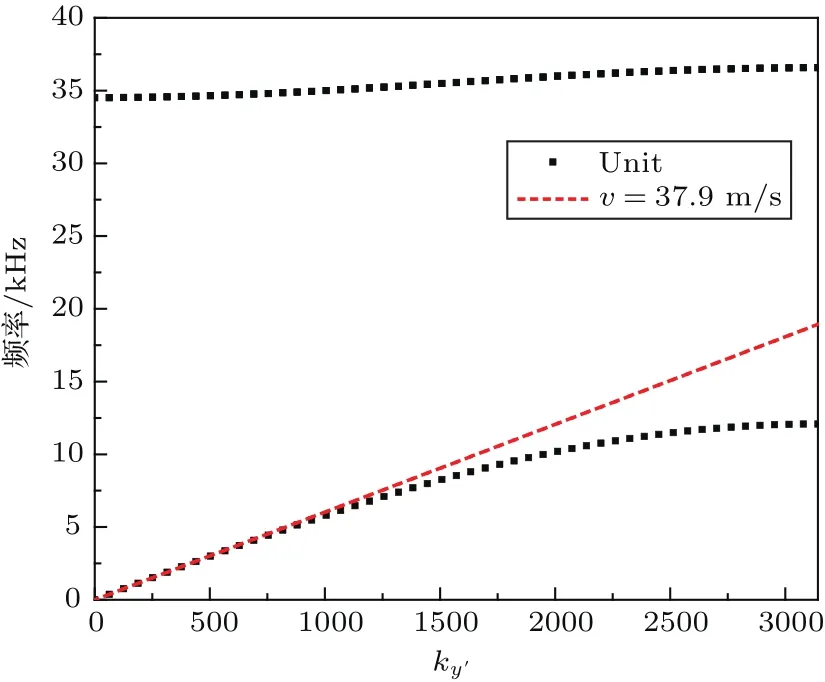
图4 单元能带曲线Fig.4 Band structure of the layered unit

3 仿真分析

使用有限元软件COMSOL可以对实现的器件进行声场仿真，其中，声反射器的结构尺寸为a=160 cm，b=20 cm。按照图2(a)所示进行分层，蓝色层为介质A(ρA=21.99 kg/m3，κA=2.62 MPa)，黄色层为介质B(ρB=0.07 kg/m3，κB=7.93 kPa)，层状结构与x轴夹角α =6.42◦。每层厚度为t=0.5 mm，形成厚度为1 mm的分层介质单元。将声反射器放置于硬地面上，以保证理想的全反射边界，如图5所示，其余的边界设置为吸收边界，以减小周围反射的影响。

频率为3 kHz的仿真声场如图5所示。图5(a)中，左边一束高斯波从上向下垂直入射(0◦)，进入反射器之后在其内部传播，然后通过结构右侧再次向外辐射，反射方向为竖直向上(入射方向的反方向)。图5(a)中用红色箭头在反射器内部标出了声波的传播路径，声波进入结构后，受到密度各向异性介质的影响，波束传播方向发生偏折，斜入射在硬地面上，反射后又再次斜向右上方传播。由于结构的对称性，声波的传播路径也是相应对称的。经过地面的反射，波束变宽，能量密度下降，所以反射波的幅度会有所降低。图5(b)则为一定小倾斜角入射情况下的声场分布，可见当入射角增加到20◦，反射声波也仍然可以保持回向传播的特点，随着倾斜角的增加，反射波束会逐渐向入射波束靠近；当倾斜角增加到45◦时(图5(c))，此时反射波束与入射波束基本重合。继续增加倾斜角到60◦，如图5(d)所示，此时入射波与反射波的方向存在一定的夹角，反射波已经不再向入射波的方向回向传播，所以在该角度下声反射器失效。

对于一个理想的角反射器而言(图1(b))，根据简单的几何关系可知，两块相互正交的反射面可以将45◦以内的入射波按照原方向进行反射(图1(b)中黄色箭头)。如果入射角度大于45◦，反射波就会逐渐偏离入射方向。该现象与文中所设计的反射器的效果一致，因此证明了这种正面凸起向上的超材料结构也能够达到角反射器的效果。

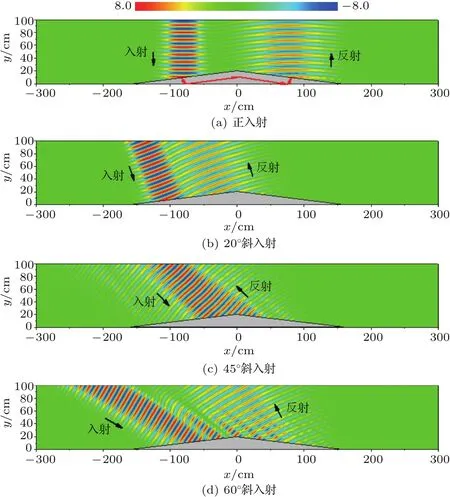
图5 声反射器的有限元声场仿真Fig.5 Simulated acoustic pressure f i elds of the retrodirective ref l ector by FEM

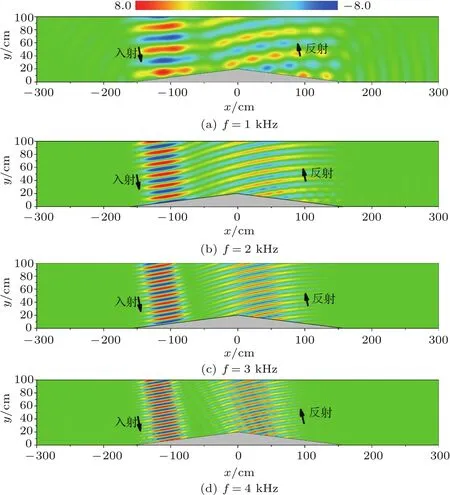
图6 不同频率下的仿真声场Fig.6 Simulated acoustic pressure f i elds of the retrodirective ref l ector at dif f erent frequencies

为了验证结构的宽频有效性，图6给出了声波以10◦入射情况下，使用不同频率的高斯波束作用于声反射器的仿真声场。图6(a)∼图6(d)分别对应于频率为1 kHz、2 kHz、3 kHz、4 kHz的声场，图中左侧为入射波束，以10◦小角度入射到结构表面，然后经过结构内部将声波引导至右侧，仍然以10◦斜向左上方传播。对于1 kHz、2 kHz、3 kHz、4 kHz的声波，其反射波都保持回向传播的特点，因此该反射器在这段频率范围内都能有较好的效果。它的工作频带与图3中单元所表现出的稳定区间一致，实际上整体结构是由一系列单元按照特定的方式排布而成的，很显然单元的特点也就决定了反射器的特性。在本文中，单元具有宽频且稳定的各向异性的特点，因此设计的反射器也就相应的能够在宽频、多角度下工作。图5中的仿真证明了结构的有效工作角度范围，而图6中的仿真则验证了结构的宽频有效性，这与上述结论相符。

4 结论

利用变换声学理论，本文提出了一种线性变换的声反射器。这种声反射器需要利用密度各向异性的超材料进行实现。结合Biot流体理论，本文设计了一种具有强各向异性的超材料单元，并利用其构建了声反射器。仿真实验表明，该反射器可以改变反射声波的传播方向，在45◦范围内，无论声波从任何角度入射，反射波都会朝入射方向进行回向传播，从而显著增加回波强度。此外，仿真实验同样验证了该结构的宽频有效性。基于超材料的声反射器可调性强，宽频有效，易于安装布放，因此具有较强的实用价值。