射线模型Bellhop的并行化处理

张朝金孙炳文1,2†

(1中国科学院水声环境特性重点实验室 北京 100190)

(2中国科学院声学研究所 北京 100190)

(3中国科学院大学 北京 100049)

0 引言

射线法具有成熟的理论基础，适用范围广且其物理图像清晰，基于射线追踪技术的射线模型被广泛应用于水下声场快速预报[1]、海洋声层析[2−3]、三维声场计算[4−5]、匹配场定位[6]等水声领域。同时，将射线理论与简正波等模型相互结合，可以建立有效的适用于复杂环境中的低频声场计算模型[7]，或可用于分析复杂环境下声场特性的变化规律[8]。

由于传统射线方法在方程建立与求解上的限制，无法有效计算声影区和会聚区的声场。几何衍射理论可以处理声影区的计算问题，但该理论中声束宽度的微小设置误差会导致很大的计算问题[1]；W.K.B.近似方法可以有效计算会聚区声场，但是该近似解难以推广至二维和三维的水声传播情况[9]。20世纪80年代，Porter等[10]提出了高斯射线追踪理论，通过更加宽容的高斯函数表征声波强度在声波束管中的分布，有效地解决了经典射线方法中声影区和会聚区声场能量不准确的问题和声束宽度设定的限制。对于高频、与距离有关(简正波、快速场、抛物理论不适用)的海洋声传播问题，该模型计算更准确，在计算精度和实时性上都有很大的提高。基于高斯声线束理论的Bellhop声场计算模型的出现也加快了高斯声线束模型的广泛应用。

随着我国对海洋的研究由浅海向深海、由近场向远程的探索，对实时且准确预估声场提出了越来越高的要求。随着计算机计算能力的飞速提高和并行计算技术的快速发展[11]，水下声场并行计算成为声场快速预估的有效途径，充分利用计算机多核计算能力，将声场计算并行化，是提高声场计算效率最简单、直接的方法，对于该问题的研究已经成为水下声传播的热点问题之一[12−13]。高斯射线束(Gaussian ray bundle,GRAB)理论具有计算速度快、物理意义清晰并且适合并行化处理等优点，许多学者就射线理论并行计算声场展开了一系列的探究。其中较为简单的就是应用OpenMP在共享存储的模式下进行并行计算，但OpenMP不适用于集群。因此，陈连荣等[14]利用基于消息传递编程模型(Message passing interface,MPI)进行了高斯射线声场模型并行算法的设计和编程，该方法可以应用于多处理器集群系统。MPI适合各种机器，但是其编程模型复杂，程序可靠性差。

综上所述，本文基于高斯射线束理论探究Bellhop模型的数值计算原理与并行计算的可行性，考虑现有并行方法的优缺点，利用多线程技术，开发出并行化射线模型BellhopMP(Bellhop multi process)，并且对BellhopMP的并行效率进行了测试与分析，从而快速、准确地预报声场。

1 并行化射线模型设计

1.1 高斯射线理论与Bellhop声场计算模型

考虑二维柱坐标系下声场的Helmholtz方程：

式(1)中，c为声速，ω为声源处的角频率。根据级数解形式p(r,z)=exp(iωτ)An/(iω)n，忽略高阶项，可得程函方程和强度方程：

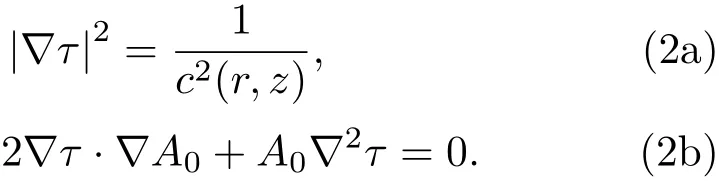
引入射线坐标和射线束概念，可分别获得描述射线束中心声线的控制方程和射线束强度的表达式：

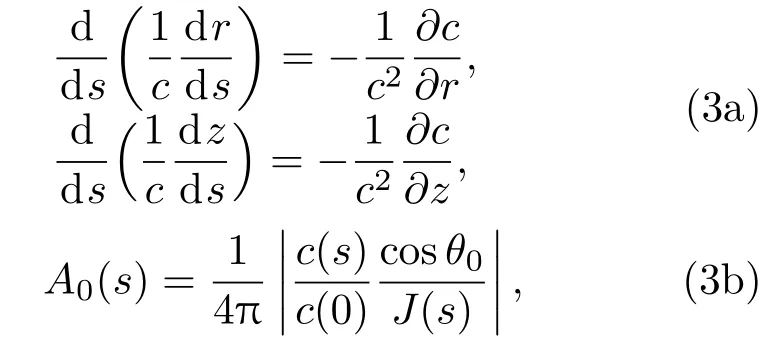
其中，s为射线坐标中的声线弧长量，θ0为声线的初射掠射角，[r(s),z(s)]描述声线轨迹，|J(s)|为表征柱对称情况下引入的几何扩展量和s处相邻声线间的弧长变化。

根据|J(s)|所表征的物理意义，并结合射线坐标，针对经典的射线理论，可建立|J(s)|计算表达式和动力学射线方程，即

其中，p和q为射线坐标s处相邻射线之间的弧长及其相对变化。

高斯波束跟踪方法，不仅保留了传统射线的一些优点，还能够避免传统射线的实际应用困难。在水声学研究领域，目前存在几种典型的高斯波束跟

踪方法，理论基本相似，主要区别在于波束内部声场能量的分布形式、沿波束行进过程中能量扩展形式等方面。高斯射线束方法，通过引入较为简单的波束宽度限制，可以较为准确地处理简单的声影区和会聚区声场问题。高斯射线理论的基本思路是将声线看作截面能量按照高斯函数分布的声束，该声束的中心声线满足标准的控制方程，如式(3a)所示，在中心声线邻域可以构造出

其中，η是距离中心声线的垂直距离；A是一个任意的常数，通过与均匀介质声场参考值比较，由声源性质确定；τ(s)为沿声线的相位延迟；p和q为在上文基础上由高斯波束束宽和曲率定义的复弧长及相对变化。考虑点源问题，声场的射线理论表达式为

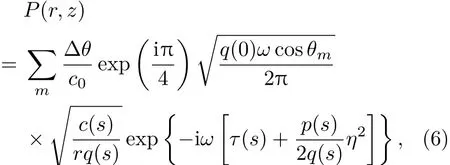
式(6)中，∆θ为声束的夹角，θm为相应声线的掠射角，τ(s)在控制方程计算的基础上进行求解，p和q则在高斯波束束宽和曲率给定的初始值下根据动力学射线方程(4b)计算。

Bellhop就是基于高斯声线束理论开发的声场计算模型，其计算准确性和可靠性已经得到重复检验。该模型宽容性较好，可以应用高斯、帽型等波束进行声场修正，且可以获得传播损失、本征声线以及声线到达时间序列等多种实用数据，同时可以处理海面、海底和声速剖面随距离变化的情况。Bellhop允许输入设计好的具有指向性的声源，可以通过输入具体的地声参数或者通过海底反射系数表征海底边界进行声场计算。模型从提出至今已发展出多个不同的版本，利用不同的编程语言发展出Fortran版、Matlab版、Python版。本文为了方便进行并行化模型的设计，把Fortran语言版本的源程序移植为C++语言版本：BellhopC，C++版本的Bellhop可以在不支持Fortran语言的平台中使用。

1.2 BellhopMP并行化射线模型设计

高斯射线模型Bellhop的声场计算中每条声线对声场的贡献是独立叠加的，即各条声线计算之间没有直接联系，因而非常适宜按照不同的射线计算来分配任务。因此可以在声线层面上进行并行化处理，将声线跟踪及对声场的贡献分配到多个计算核心上进行计算，然后合并声场即可得到考虑所有声线贡献的声场。

根据高斯射线模型的特点，并行化模型BellhopMP对Bellhop的并行化体现在声线分组和声场合并，并行过程如图1所示。BellhopMP读取计算参数文件，根据用户设定的线程数量进行多核并行计算；如果用户不指定线程数量，则使用硬件系统能提供的最大并行能力。在主线程中执行Bellhop的所有计算流程，读取声线初射角度信息后，根据可以使用的并行能力，将声线角度分为多个区间，主线程只计算第一个区间的声线及其对声场的贡献。其他每个线程计算某一个声线角度区间的声场结果。最后在主线程中合并所有的声场计算结果，输出到结果文件中。

图1 声场计算模型BellhopMP并行处理流程Fig.1 Flow chart of BellhopMP

2 并行计算算例分析

图2 Pekeris波导情况下Bellhop、BellhopC与BellhopMP的声场计算结果Fig.2 The sound f i eld computed by Bellhop,BellhopC and BellhopMP in the Pekeris waveguide

为了检验并行算法的准确性，实验过程中对Acoustic Toolbox中多个算例使用Bellhop、BellhopC和BellhopMP进行了计算分析，得到的结果基本一致，基本验证了并行射线程序BellhopMP的准确性和可靠性，文章中只列出了经典情况(calibB_gb和MunkB_Coh_gb)下的结果。浅海Pekeris波导情况下，环境参数和几何参数为水中声速1500 m/s，海底为声速1590 m/s、密度1.2 g/cm3、衰减0.5 dB/λ的液态半无限空间；海深100 m，接收距离5 km，声源深度50 m，频率250 Hz。Bellhop、BellhopC和BellhopMP声场计算的传播损失结果如图2所示，Bellhop和BellhopC相对于BellhopMP的计算结果误差分布(x轴为两者计算得到的传播损失的差，y轴对应该差值的个数)如图3所示。

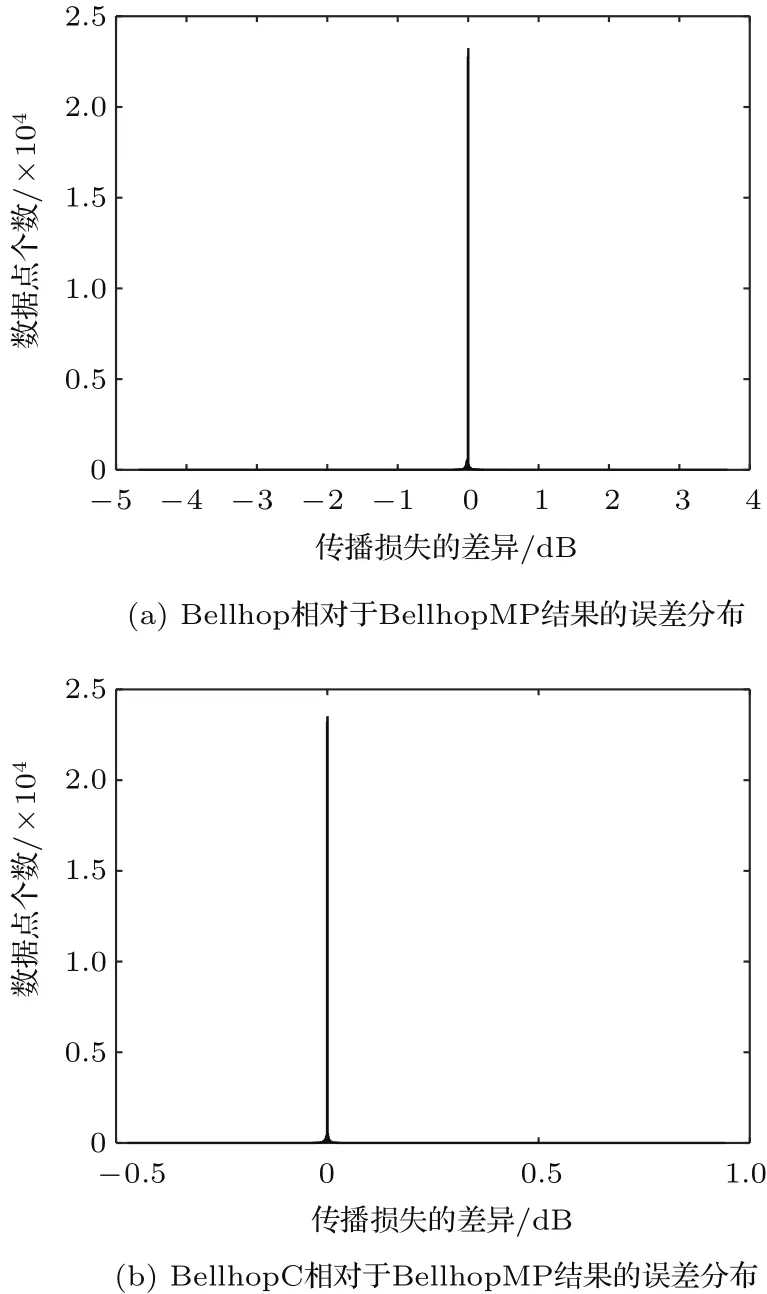
图3 Pekeris波导情况下不同版本Bellhop模型的声场计算结果误差分布Fig.3 The error distribution of dif f erent versions of Bellhop in the Pekeris waveguide

典型深海Munk剖面情况下，声速剖面如图4所示，其他环境参数和几何参数为海底为声速1600 m/s、密度1.8 g/cm3、衰减0.8 dB/λ的液态半无限空间；海深5000 m，接收距离100 km，声源深度1000 m，频率50 Hz。Bellhop、BellhopC和BellhopMP声场计算的传播损失结果如图5所示，Bellhop和BellhopC相对于BellhopMP的计算结果误差分布如图6所示。

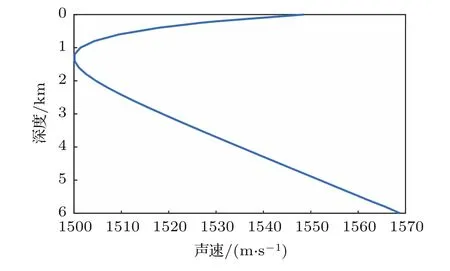
图4 Munk声速剖面Fig.4 Munk sound speed prof i le

图5 深海情况下Bellhop、BellhopC与BellhopMP的声场计算结果Fig.5 The sound f i eld computed by Bellhop,BellhopC and BellhopMP in deep water

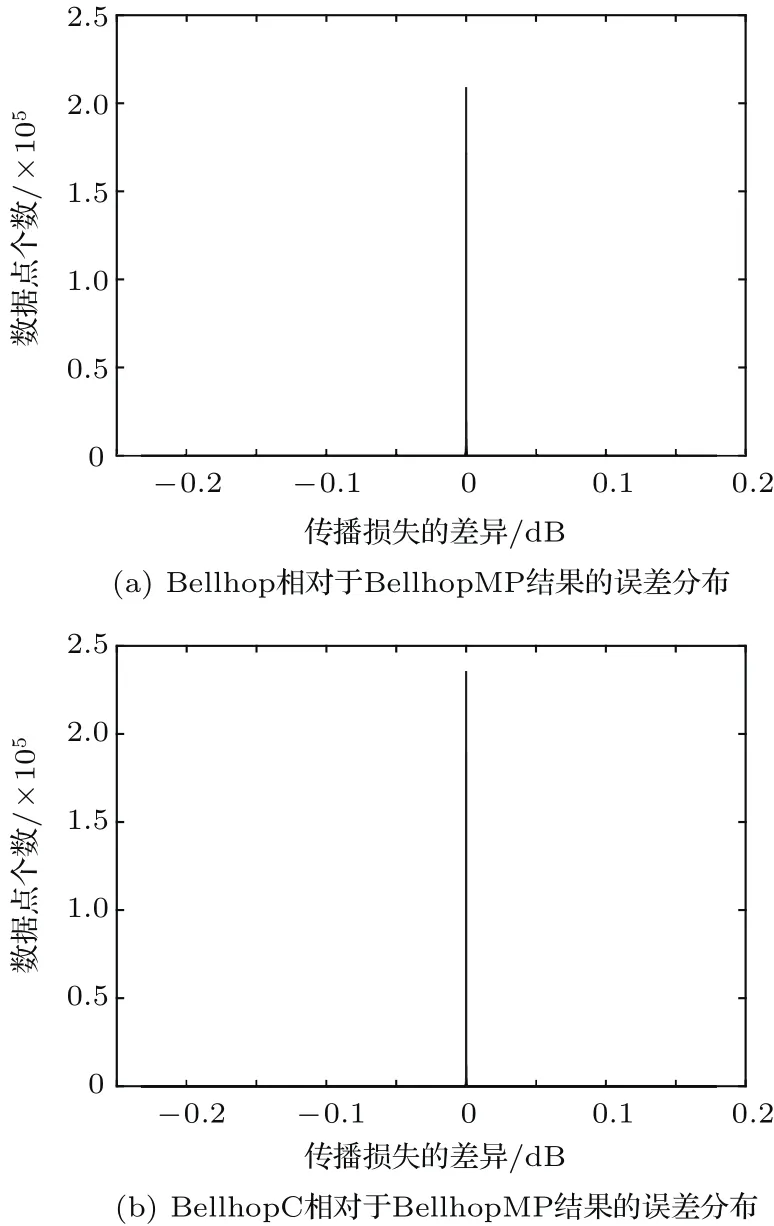
图6 深海情况下不同版本Bellhop模型的声场计算结果误差分布Fig.6 The error distribution of dif f erent versions of Bellhop in deep water

数值计算的结果显示BellhopMP与Bellhop、BellhopC计算结果一致，误差的产生是由于浮点数的表示及累积误差，对声场计算的精度没有影响，这验证了BellhopMP计算的准确性。同时，由浅海和深海环境下的声场计算结果可以看出，基于高斯波束的射线模型可有效实现水下声场的计算，在浅海中声线相互干涉从而体现简正波传播特征，而在深海中可有效给出声影区和会聚区的声场值。

3 并行效率

本文使用Intel(R)Core(TM)i7-4770K CPU@3.50 GHz和Intel(R)Xeon(R)CPU E3-1505M v6@3.00 GHz两种CPU进行并行计算效能的测试，两种CPU都是4个核心，在超线程技术的支持下，可以进行8个线程的同时计算，以发挥CPU的最大计算能力。操作系统均为Windows 10。对于所有算例分别使用Bellhop、BellhopC、BellhopMP(依次设置线程数为1∼8)、BellhopMP(默认参数，使用全部可用的线程数)计算100次，统计每个算例计算耗时的均值和方差。以经典深海情况(MunkB_Coh_gb)为例，其环境参数和几何参数见图5的计算说明，其均值与标准差结果如图7所示。

以上两种CPU下的计算结果趋势一致，如图7所示。但是在Xeon处理器上，耗时的方差较大，这应该与CPU的架构差别有关。BellhopC的耗时比Bellhop的多，这与Bellhop的C++语言实现的效率有关，有进一步优化的可能。需要说明的是，对于计算一条声线的声场，BellhopMP并没有使用多线程来计算，且当算例的计算耗时很少时，由于BellhopMP需要额外的任务分配和结果合并操作，导致计算时间相对于BellhopC并没有减少，有时计算时间反而会增加。

为了定量描述并行计算的能力，定义并行效率(P)为加速比与线程数目之比，反映执行并行算法时，平均每个处理器的执行效率。其中加速比为同一个任务在单处理器系统和并行处理器系统中运行消耗的时间的比率：

T1是在单个处理器下的运行时间，TN是在有N个处理器并行系统中的运行时间。

根据图7的计算结果，取T1为Bellhop的运行时间，BellhopMP在不同线程下相对于Bellhop的并行化效率如图8所示。BellhopMP采用大粒度的并行处理，在主线程中不仅计算声场，还负责声线区间的分割和声场计算结果的合并。这导致了随着线程数量的增加，时间减小得越来越不明显，并行效率逐渐降低，如图8中i7 CPU在使用4个线程时并行效率只有0.5，这是由于Fortran版本的Bellhop的计算时间只有12 s。

并行效率与串行的计算时间有关，串行时间越长，并行效率越高。如图9所示为使用Acousitc Toolbox中提供的测试算例(arcticB_cpp、DickinsCervenyB、MunkB_Coh_CervenyR、MunkB_Coh_gb、MunkB_Coh_SGB、MunkB_gbt)，皆使用4个线程(与CPU的核心数相同)时的并行效率。由图中结果可以看出，随着串行计算时间的增加，并行效率逐渐增加。如图9(a)中可以看出，当Bellhop计算时间为105 s时，i7 CPU的并行效率可达0.9。因而，对于远距离深海环境下的长时间声场计算问题，本文提出的并行模型可在保证计算准确性的前提下，有效提高计算效率，减少计算时间。

图7 各类计算方式耗时的均值和标准差。其中，F、C、1–8、A依次表示Bellhop、BellhopC、BellhopMP(线程数1∼8)、BellhopMP(默认参数)Fig.7 The mean value and standard variance of computation time cost by dif f erent models on two platform.F,C,1–8,A represents dif f erent models:Bellhop,BellhopC,BellhopMP(thread count:1∼8),BellhopMP(default)

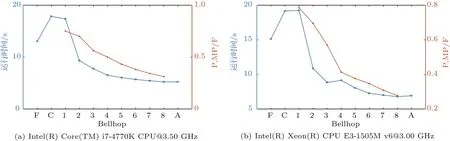
图8 不同线程数目时BellhopMP相对于Bellhop的并行计算效率Fig.8 The parallel efficiency of BellhopMP using dif f erent count of thread on two platforms

图9 串行模型Bellhop的计算时间和使用4个线程的BellhopMP的并行效率之间的关系Fig.9 The relationship of serial computation time and parallel efficiency of BellhopMP using 4 threads

4 结论

本文在分析高斯射线束理论的基础上，根据射线模型的特征，利用多线程技术对射线模型Bellhop进行了并行化处理，开发了并行化射线模型BellhopMP，该模型在保证计算结果准确性的同时，在多核计算机上能大幅度提高计算速度且有较好的并行效率，可以解决深海远程以及复杂情况下声场计算时间过长的问题。同时该模型串行时间越长，并行效率越高，故对于深海超远程等长时间声场计算问题，BellhopMP可有效降低计算时间，而对于耗时较短的声场计算，并行效率提高的程度有限。相较于其他并行方法，BellhopMP并行化处理方式简单易行，程序可靠性较高，这种并行化处理方式也适用于DSP(Digital signal processor)等多核心处理器计算平台。