T型两亲性高分子在溶液中的自组装微结构及其转变规律

2019-03-30李庆飞王志远王向红季永运李士本

温州大学学报（自然科学版） 2019年1期

李庆飞，王志远，王向红，季永运，李士本

(温州大学数理与电子信息工程学院，浙江温州 325035)

聚合物及软凝聚态体系通过平衡态的自组装或者非平衡态的动力学演化能形成空间有序的微相结构[1].具有不同拓扑结构的聚合物如星型嵌段共聚物、接枝嵌段共聚物等往往能够形成复杂的微相结构.T型两亲性高分子是由化学性质不同的嵌段通过化学键相连接而组成，它包含一个两端被端基取代的亲水性棒状芳香核心，一条疏水性的柔性侧链连接在亲水性刚性棒的中心位置[2-5].近年来，无论在实验方面还是在理论模拟方面，T型两亲性高分子都受到越来越多的关注.

实验方面，Kieffer等[6]实验研究表明，T型两亲性高分子的分子内和分子间氢键的竞争会导致微相分离不稳定；同时，Glettner等[7]也采用X射线衍射方法来研究T型高分子的微相结构.在选择性溶液中，T型两亲性高分子可以自组装形成多种超分子结构.例如，Tschierske等[8-9]运用偶合反应制备出丰富的多边形蜂窝柱状相结构[10-11].Kieffer等[12]发现如果在T型两亲性高分子的基础上再引入第二条疏水链，可以防止分子并排铺陈和双壁圆筒相的形成.理论模拟方面，Xia等[13]研究了T型棒状嵌段共聚物熔体的自组装相行为.Bates等[14-15]运用DPD模拟研究了T型和X型两亲性分子的柱状相结构.Crane等[16-17]通过模拟发现，在低浓度下溶剂会溶解掉蜂窝柱状相结构，但顺序不会发生明显改变.Liu等[18]采用耗散粒子动力学模拟研究了由不相容的端链和侧链连接的棒状核心组成的T型三元两亲性高分子的相行为.Sun等[19]研究了具有燕尾侧链的T型两亲性高分子，通过改变温度和侧链长度，得到了复杂的相结构，与实验中发现的结构一致，并研究了焓和熵与自由能下降的关系.

虽然人们对T型两亲性高分子的微相结构做了较多的研究，但是，这些研究局限于本体中的相行为，在溶液中的连续性相行为极少有人研究.本研究利用耗散粒子动力学（Dissipative Particle Dynamics，DPD）方法探究了T型两亲性高分子分别在不同浓度下的选择性溶剂中形成的不同的相结构的变化及其转变规律.

1 模拟方法与模型

1992年，Hoogerbrugge和Koelman[20]提出的耗散粒子动力学（DPD）方法是一种介观尺度的模拟方法.在DPD模拟方法中，粗粒化的粒子服从牛顿运动定律，同时有三种力作用在每一个粒子上，保守力、耗散力、随机力产生一个合力

计算牛顿积分方程时采用修正的Verloeity-Verlet[21]算法.各个力表示为：

其中kB是玻尔兹曼常数.公式（4）中的aij是高斯统计下的随机波动变量：＜θij(t)＞=0和匹配水需求的压缩性，相互作用强度aij与Flory-Huggills参数χij存在以下关系：

本文研究中，粒子数密度ρ设为3，上述中aij表示DPD粒子之间的保守力强度，其中aij是粒子之间的排斥系数，同种粒子之间的保守力强度设置为20，亲水性粒子与疏水性粒子之间的保守力强度设置为60，亲水性粒子与水之间的保守力强度设置为20，疏水性粒子与水之间的保守力强度设置为120.分子内相邻粒子之间靠谐振势化学键合，谐振势的形式为

其中C=10为弹簧系数.

为了维持T型两亲性高分子的拓扑形状不变，分子内部每相邻3个粒子之间施加弯曲势，弯曲势的表达式：Fθ=-∇[kθ（θ-θ0）]2，kθ表示的是弯曲常数，以图1为例，亲水性链段之间的kθ=4，疏水性链段之间的的kθ=2.θ表示的是相邻键与键之间的夹角，θ0表示的是平衡时候的夹角，除了图1中特别标明的θ0=90°，其余都是θ0=180°.NMB为亲水链段的单体数，NSB为疏水链段的单体数.

为了方便计算，在DPD模拟方法中的物理量都采用无量纲的常数，即rc=m=kBT=1.溶液中的溶质是T型两亲性高分子，溶剂是水，模拟中用1个DPD珠子来表示1个水分子.T型两亲性高分子的主链与水是相互吸引的，具有亲水性，我们称之为亲水性主链；T型两亲性高分子的侧链与水是相互排斥的，具有疏水性，我们称之为疏水性侧链.在图1中，亲水性头珠以红色和绿色表示，疏水性尾珠以黄色表示.

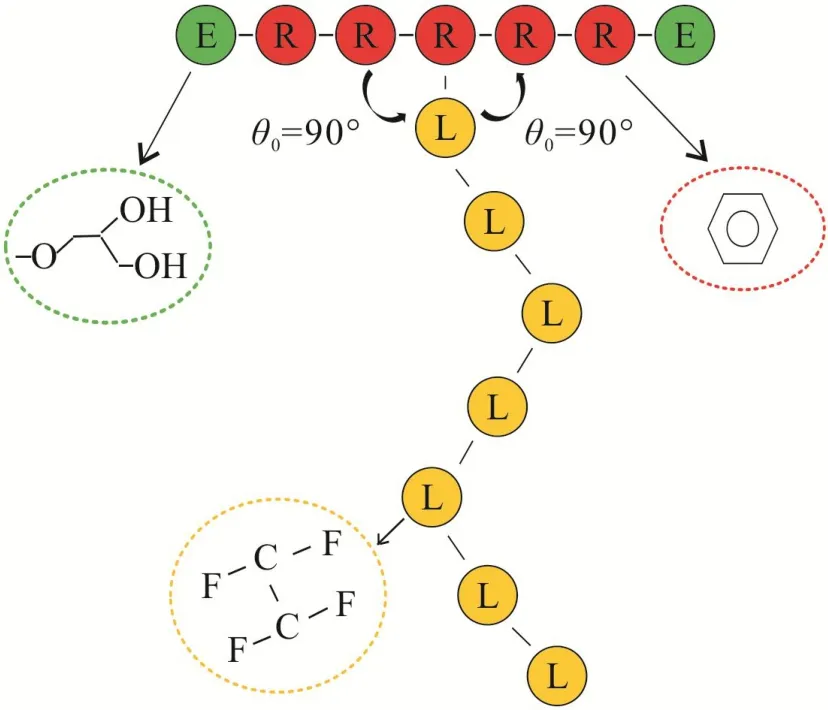
图1 具有头基和尾基的T型高分子的示意图Fig 1 The Schematic Diagram of T-type Macromolecule with Head and Tail Groups

2 结果与讨论

2.1 T型两亲性高分子的自组装微相结构

本文采用耗散粒子动力学模拟（DPD）方法研究T型两亲性高分子在选择性溶液中的自组装.我们研究了T型两亲性高分子在三种浓度下的相行为，分别得到了球状相、柱状相和穿孔层状相等一系列相结构，见图2.

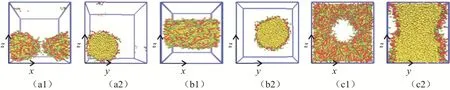
图2 T型两亲性高分子在溶液中形成的相结构Fig 2 The Phase Structure of T-type Amphiphilic Polymer in Solution

其中a1和a2的相关参数为：NMB=10，NSB=14，浓度为0.15.形成了球状相，亲水链在外，疏水链被亲水链包裹着.这是因为亲水链比亲水链与水的相互作用更强.b1和b2的相关参数为：NMB=6，NSB=18，浓度为0.30.形成了柱状相，亲水链在外，疏水链被亲水链包裹着.这是因为浓度为0.30时，疏水链的体积占比变大，才形成柱状相的.比较Tschierske等[8-9]运用耦合反应，在实验上制备出的相.本文新发现了球状相，这可能是由于溶剂的诱导作用.c1和c2的相关参数为：NMB=6，NSB=20，浓度为0.60.形成了穿孔层状相，亲水链在外，疏水链被亲水链包裹着.从俯视图看上去中间有一通透的圆孔；从侧视图看上去，像双层膜结构.这三种自组装相结构与Liu等[18]的实验结果一致.

2.2 T型两亲性高分子的相图

图3是在0.15，0.30和0.60三种浓度下构建的T型两亲性高分子的相图.图3中的NMB代表模型中的E与R珠子，图中的NSB代表模型中的L珠子.圆点代表球状相，圆柱代表柱状相，有孔四边形代表穿孔层状相.

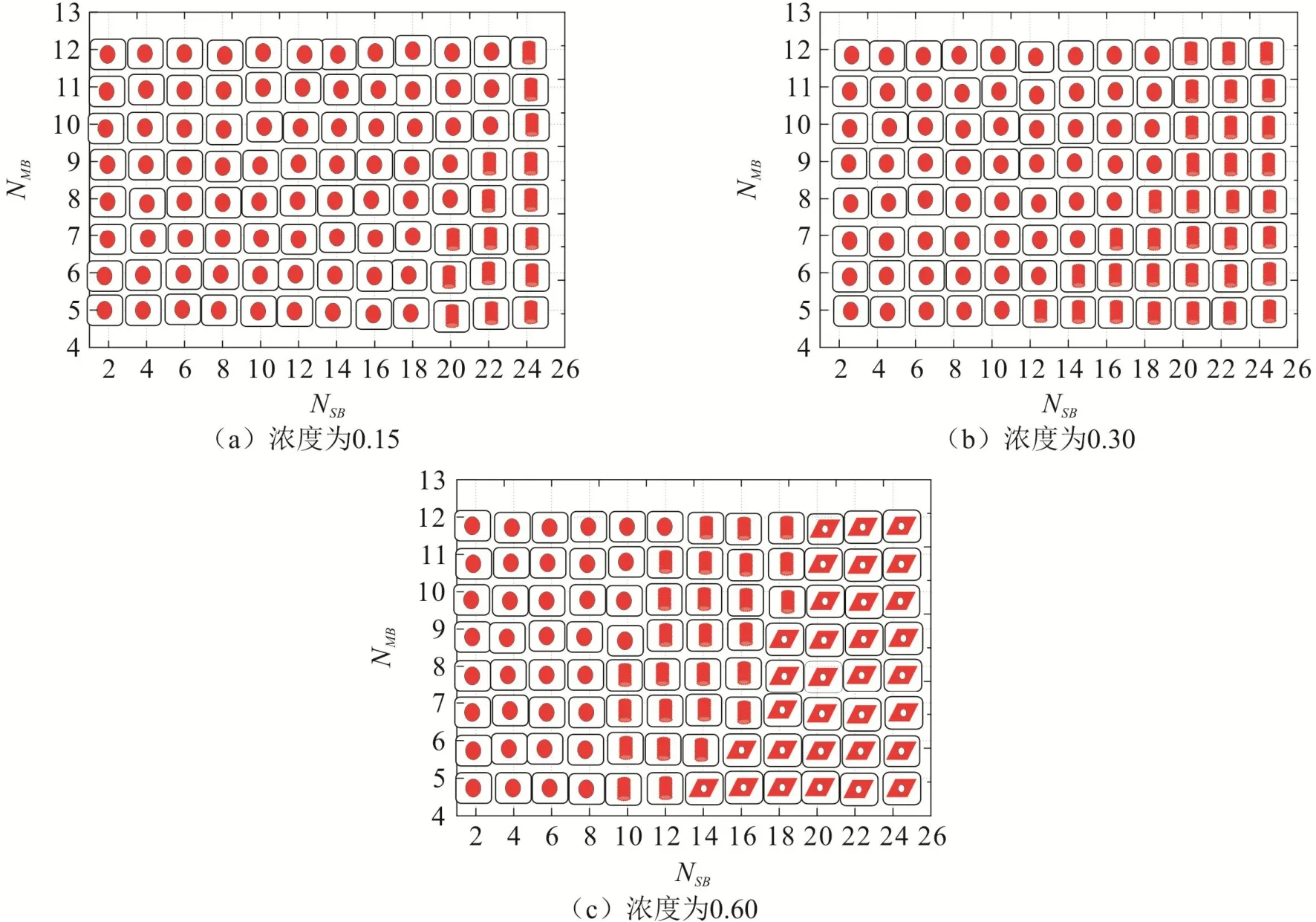
图3 在三种浓度下构建的T型两亲性高分子的相图Fig 3 The Phase Diagrams of T-shape Amphipathic Polymers Constructed at Three Concentrations

在浓度为0.15条件下，通过改变亲水链长度与疏水链长度，构建了体系的相图，见图3（a）.由图可见随着疏水链长度的增加，溶液中的球状相逐渐变大最后形成了柱状相.以上构型发生转变是因为随着疏水链长度的增加，疏水部分占得比例增加，相结构从球状逐渐变大成柱状.亲水链长度的增加，不利于柱状胶束的形成.这是因为亲水链在外面包围着疏水链，亲水链长度的增加可以提供更大的表面积，不利于柱状胶束的形成.

在浓度为0.30条件下，通过改变亲水链长度与疏水链的长度，描绘出体系相图，见图3（b）.本图中的变化规律与浓度为0.15时的类似，但与浓度为0.15时相比，浓度为0.30的体系中，球状相与柱状相的尺寸也相应增大了.

在浓度为0.60的条件下，继续改变亲水链的长度与疏水链的长度，构建了体系的相图，见图3（c）.这次我们找到了穿孔层状相.穿孔层状相明显不同于球状相和柱状相，这是因为随着T型两亲性高分子浓度的提高，出现了一个明显的浓度节点，疏水粒子有连成一层的倾向，然而还不足以形成层状，所以中间出现了层与层之间的通道形成了穿孔层状相.穿孔层状相可以使亲水粒子在水中更好的包围疏水层状相，降低体系的吉布斯自由能，使T型两亲性高分子更好地存在于溶剂中.

纵观这三幅相图，发现这三幅相图与Bates等[14-15]得到的T型两亲性高分子的相图有些差别，是因为Bates等不仅改变了链长，而且还改变了结晶温度.而我们的创新在于改变T型两亲性高分子的疏水侧链长度及亲水主链长度.

图4 球形胶束和柱状胶束的直径随NSB珠粒而变化Fig 4 The Diameter of Spherical Micelles and Columnar Micelles Varies with NSB Beads

图4（a）以及图4（b）中的纵坐标为无量纲的常数，单位为1.图4（a）中球形胶束的直径的变化浓度为0.15，分析球状胶束的直径，发现随着亲水链长度的增加，球状胶束的直径呈增大趋势，说明得到的球状胶束是合理的.我们选取了疏水链长度分别为12、14和16的球状胶束，分别统计了它们的直径大小.随着亲水链长度的增加，球状胶束的直径逐渐增大.

接着我们分析柱状胶束的直径，见4（b），柱状胶束直径的变化浓度为0.30.随着亲水链长度的增加，柱状胶束的直径呈增大趋势，说明我们得到的柱状胶束也是合理的.我们选择了疏水链长度分别为20、22和24的柱状胶束，分别统计了它们的直径大小.随着亲水链长度的增加，柱状胶束的直径逐渐增大.与Tschierske等[8-9]运用耦合反应，在实验上制备出的相结构对比，本文中的柱状相的直径增加更快一点，可能是我们的模拟存在一定程度的误差.

2.3 穿孔层状相的动力学过程

图5 具有两种初始输入的穿孔层的动力学过程Fig 5 The Dynamic Process for Perforated Layer Membranes with Two Initial Inputs

图5显示了形成穿孔层状相的动力学过程中经历的两种状态.由于穿孔层状相的不同初始状态，导致了不同的动力学过程.图5（a）是无规散乱分布的初始状态，中间在21 000步的时候出现了两个小孔，然后在21 000-72 000步之间两个小孔逐渐变大，最后到达平衡，形成穿孔层状相.图5（b）是层状分布的初始状态，中间在30 000步的时候出现了一个扁孔，然后在30 000-84 000步之间一个扁孔逐渐变大，最后形成穿孔层状相，到达平衡.图5的动力学过程与Giang等[22]研究的动力学过程都是随着时间的推移，总能量趋于最小值，到达平衡态，中间的动力学过程却不唯一.