一类有紧支集Novikov型方程的大时间行为
2019-03-30曹亚强郭正光
曹亚强,余 闯,郭正光
(温州大学数理与电子信息工程学院,浙江温州 325035)
Novikov方程
是Vladimir Novikov在对称分类中发现的具有三次非线性的非局部偏微分方程[1],Novikov方程被证明是可积的.Rodríguez-Blanco在文献[2]中证明了方程(1)在Sobolev空间中的适定性,Ni和Zhou在文献[3]中证明了方程(1)在Besov空间中是局部适定的,其中s=32是适定的临界指数[4],Yan等[5]证明了方程(1)在Besov空间中局部适定性的某些假设,并且表明方程(1)在Sobolev空间Hs(ℜ),s<中是不适定的[6].我们在本文中将方程(1)推广为以下方程:
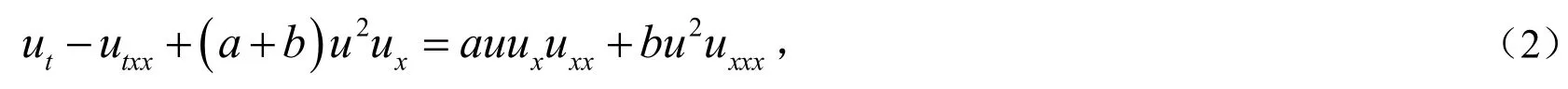
相关的初值u(x;t=0)=u0(x),这里的a>0,b>0是任意的常数,初始动量y(0,x)=u(0,x)-uxx(0,x)(简记为y0)非负且具有紧支集.在本文中,无穷远处的零边界条件已经被施加于u(x,t)和它的所有可能的导数,除了a=3和b=1(在方程(1)中)之外,方程(2)的可积性仍然不确定,所以本文的主要目的是讨论这些系数如何影响解的大时间行为.通过对方程Camassa-Holm和Degasperis-Procesi的深入研究,我们试图选择a和b的适当关系来讨论方程(2)的大时间行为.Li等在文献[7]中对方程(2)的持续性质和爆破现象进行了探讨,基于Kato的半群理论[4]可以证明方程(2)的局部适定性,根据Ni和Zhou在[3]中所作的工作,这里我们跳过它的细节,重点关注解的动量支集的大时间行为,证明在全局解存在的条件下,随着时间趋于无穷大动量支集也足够大.
1 准备知识
介绍一些基本的符号和属性.假设u(x,t)是方程(2)的一个光滑解,并且y(x,t)=(1-)u(x,t),于是u(x,t)和ux(x,t)能够表示为:

从(3)式和(4)式可以直接得知:

另一方面,为了方便讨论方程(1)的等价形式为:

为了定理证明,引入特征方法.设q(x,t)是随着解u(x,t)发展的粒子轨迹,并且满足方程初始值q(x, 0)=x,易看出q(x,t)是一个单调递增的同胚线,它保持

事实上,通过直接计算有:

为了方便介绍,引入以下符号:
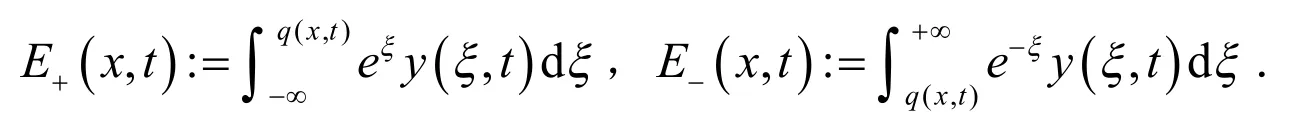
通过简单的计算,对于E+(x,t)有:

类似地,对于E-(x,t)有:

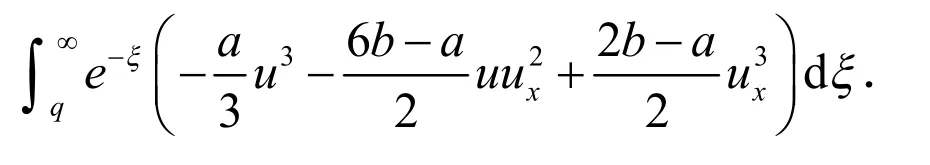
2 大时间行为
本节研究具有紧支集的解的大时间行为以及初始值保持它的符号不变性.这里只关注a=b3的情形,因为有可能确定E+(x,t)和E-(x,t)的单调性对于我们的研究至关重要,这个灵感来自于(5)式、(8)式和(9)式.以下是结果.
定理1 假设y0(x)在区间[m,n]上具有紧支集,并且保持符号不变.如果a=3b,则当t→+∞时,有:

证明:通过(8)式得到:

类似地,

如果y0(x)≥0,从(7)式可以知道,y(x,t)≥0在上有紧支集,并且从(3)式和(5)式可以有u(x,t)≥0以及u+ux≥0,因此对于(11)式和(12)式有:

E+(t)和E-(t)的单调性也意味着I(t)是严格单调递增的,II(t)是严格单调递减的.由于II(t)是严格单调递减并且是正的,所以当t趋向与+∞时,II(t)的极限存在,我们称

从(7)式可以得到:
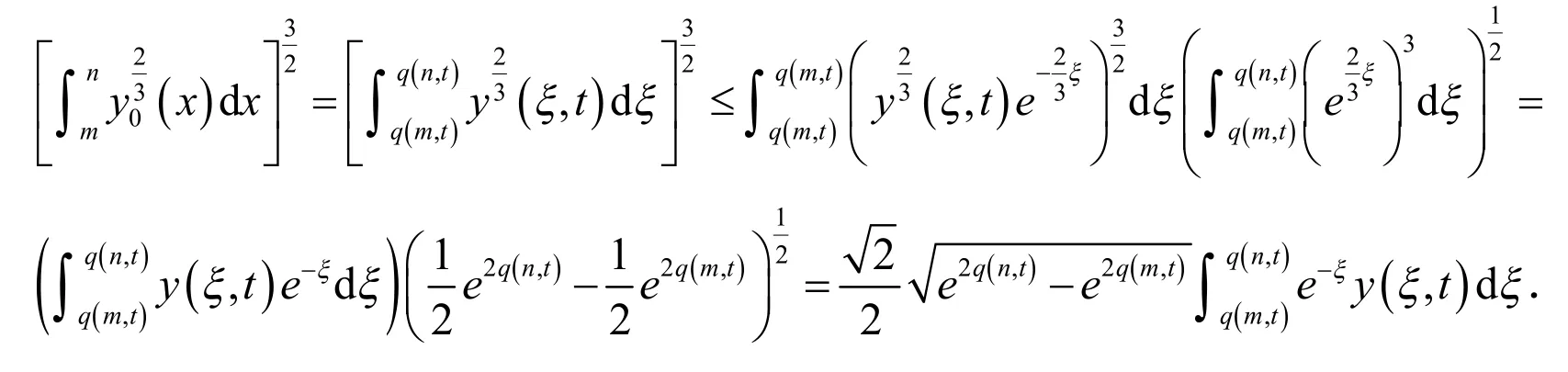
然后有:

因此从(15)式的角度看,当t→+∞时,e2q(n,t)-e2q(m,t)→+∞.
如果y0(x)≤ 0,可以通过类似的方法,很容易得到
注意到I(t)是单调递减的,而II(t)是严格单调递增并且是负的,所以可以通过矛盾来证明
利用HÖlder's不等式,有:

化简得到:

然后可得到当t→∞时,e2q(n,t)-e2q(m,t)→+∞.
