三维不可压Boussinesq方程组的正则性准则*
2019-03-29郭香香郭聪冲
郭香香,郭聪冲
(1. 暨南大学信息科学技术学院,广东 广州 510632; 2. 龙岩学院数学与信息工程学院,福建 龙岩 364012)
考虑三维不可压Boussinesq方程组:
(1)
其中u(x,t)=(u1(x,t),u2(x,t),u3(x,t))表示速度场,P=P(x,t)是压强,θ=θ(x,t)是温度,ν>0是动粘度,κ>0是热扩散系数,e3=(0,0,1)T,本文令ν=κ=1。
注意到当θ≡0时,方程组(1)退化为不可压Navier-Stokes(简记为N-S)方程组。三维不可压N-S方程组光滑解的整体存在性或光滑解在有限时间内爆破的问题是千禧年七大问题之一。这个问题的主要困难是理解三维不可压流体涡旋拉伸的影响(二维不可压N-S方程组涡旋守恒)。 为了更好的理解三维不可压流体的涡旋拉伸作用,学者们提出了各种简化模型,其中Boussinesq方程组是常用的模型之一,它不仅与三维不可压流体有着相似的涡旋拉伸效果,而且在大气科学和地球物理应用中发挥着重要的作用。所以该方程组被来自不同领域的学者们广泛研究,并且对它的研究是有物理背景和意义的。
N-S方程组有一系列的研究,参见文献[1-4]等。在讨论Boussinesq方程组之前,我们先回忆一下三维N-S方程组取得的进展。Prodi等给出了当0≤t≤T时,若Leray-Hopf弱解u∈Lq(0,T;Lp(R3))满足
下面具体讨论Boussinesq方程组。对于二维Boussinesq方程组,ν,κ>0时的全局时间正则解已证。ν=0,κ>0或ν>0,κ=0的部分粘性整体正则性由许多学者们做了一系列的工作[9-11],Xu[12]证明了具有分数阶扩散项的二维Boussinesq方程组解的存在性,唯一性和正则性。然而,对于三维Boussinesq方程组,ν,κ=0时奇点的正则性是流体力学中的一个公开问题[13-15],因此考虑三维Boussinesq方程组解的正则性是一个比较有意义的问题。期间Fan等[16]和Ishimura等[17]分别提出了以下爆破准则:
(2)
▽u∈L1(0,T;L∞(R3))
(3)
之后,Qiu等[18]证明了三维不可压Boussinesq方程组的Serrin准则。更多关于Boussinesq方程组相关的成果请参见文献[19-20]等。
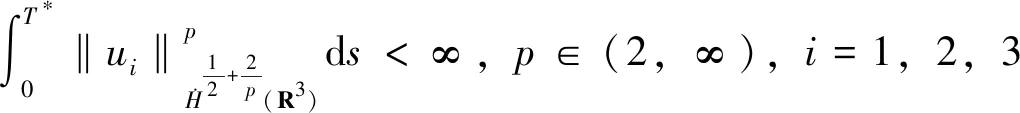
在阐述本文的主要结果之前,我们给出以下记号:
▽=(∂1,∂2,∂3),▽h=(∂1,∂2)
和
uh=(u1,u2),ω=∂1u2-∂2u1

本文的主要定理如下:
定理1 设
(u,θ)是方程组(1)在[0,T*)上的局部解,满足
且
其中p∈(2,∞),i=1,2,3
则(u,θ)可连续延拓到端点T*。
1 预备知识
在本文证明的过程中,我们将对速度场分别作水平方向和垂直方向的分解。为此,先给出一些预备知识。
定理2 记
和ω=∂1u2-∂2u1,则
(4)
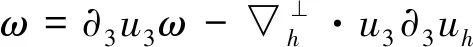
(5)
定理3 (Gagliardo-Nirenberg-Sobolev不等式)设j,m是任意正整数,满足0≤j 使得 (6) (7) 接着回顾齐次Littlewood-Paley分解的相关理论。 P>j=I-P≤j,其中I是单位算子; 为方便使用,简记: 又由φ支集的性质,当|j-j′|>1,有PjPj′=0。 进一步,我们给出仿积分解引理[8]。 引理1 对任意的f,g,h∈ζ(Rn),可得 fjg[j-3,j+3]h 发情、配种、产犊时间:荷斯坦牛第一次发情时间应小于11月龄,实际上9~10月龄发情在牛场已经很普遍。第一次配种时间推荐12.5~14月龄,随着遗传进展,荷斯坦牛13月龄体尺或体高即可达到配种要求;第一次产犊时间建议22~24月龄,平均23月龄,如果牛场做得足够好,22月龄是可以实现的,24月龄已经有点迟。 f 为证明主要定理,我们还需给出(u,θ)的H1估计。 (8) 证明由标准的能量不等式,有 先估计I1项。因为 对K1,K2项,使用Hölder不等式和插值不等式。当2 (9) |K1|+|K2|≤ (10) (11) 然后,I2项的界可简单估计为 |I2|≤C‖▽u‖L2‖▽θ‖L2≤ (12) 最后,估计I3项。由于 其中I31项可类似K1,K2项处理。下面计算I32项。由最值原理和方程组(1)的第二个方程以及第三个方程,可得:‖θ‖L∞(0,T;L∞)≤C。对I32项分部积分,有 |I32|≤C‖θ‖L∞· (‖▽u‖L2‖Δθ‖L2+‖Δu‖L2‖▽θ‖L2) (13) 综上得Ii(i=1,2,3)的界,并利用Gronwall不等式,定理得证。 为更好的证明本文的主要定理,在此之前,我们先证明两个非常重要的定理。 定理5 设ω=∂1u2-∂2u1,1 2 (14) 或 对方程(5)作标准的Lr估计,有 (15) 先估计D1项。由Hölder不等式和插值不等式,当2 (16) 然后估计D2项。注意到式(4),我们有 对于D21项,当2 (17) 和当4≤p<∞时,有 (18) 接着,估计D22项。 当2 (19) 和当4≤p<∞时,有 (20) 由式(17) -(20),可得D2项的界。 由定理4和定理5启发可得,我们仍然需要估计‖|▽h|-δ▽u3‖L2和‖|▽h|-δ▽θ‖L2的界。 (21) 证明对方程组(1)的第一个方程的垂直方向和第二个方程分别乘以|▽h|-2δ∂ku3和|▽h|-2δ∂kθ,并作标准的L2估计,可得 通过观察,可知E1,E3项和E2,E6项以及E4,E5项的结构类似。为了书写简便,我们主要估计E2,E3和E4项。 首先,估计E2项。将速度场u分别沿水平方向和垂直方向分解,可得 ▽h|-2δ∂ku3dx 和 ▽h)u3·|▽h|-2δ∂ku3dx (22) 对于 ▽h|-1ω·▽h)u3·|▽h|-2δ∂ku3dx ▽h|-1ω·▽h)u3·|▽h|-2δ∂ku3dx= (23) (24) (25) (26) 当2 (27) 和项(25)的估计 (28) 剩下的项(24),项(26)的界可类似式(27), 式(28)处理。 对 ▽h|-1∂3u3·▽h)u3·|▽h|-2δ∂ku3dx 作水平方向的Littlewood-Paley分解,同上可得 ▽h|-1∂3u3·▽h)u3·|▽h|-2δ∂ku3dx≤ (29) 由式(22)-(29),可得E2项的界。 ▽h|-1∂3u3·▽h)θ· (30) C‖▽ω‖Lr‖θ‖L∞‖|▽h|-δ∂kθ‖L2 (31) 接下来,估计E3项。 由于∂3∂kΔ-1θ=R3(θ),其中R3是三维Riesz算子,对E3分部积分,有 |E3|≤C‖|▽h|-δ∂kθ‖L2‖|▽h|-δ∂ku3‖L2≤ (32) 类似地,E1项可同E3项一样估计,此处略。 (33) ▽h|▽h|-2δ∂ku3dx=- 当2 (34) 和 (35) 由式(33)-(35),可得E4项的界。 (36) 综上将E1项至E6项的界加起来,使用Young不等式,该定理得证。 证明将定理5的不等式(14)和定理6的不等式(21)相加,利用Gronwall不等式,可得 主要定理得证。





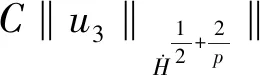



2 主要结果
2.1 水平方向项的估计

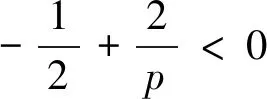
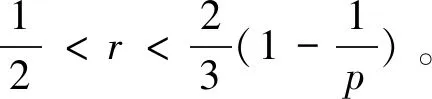

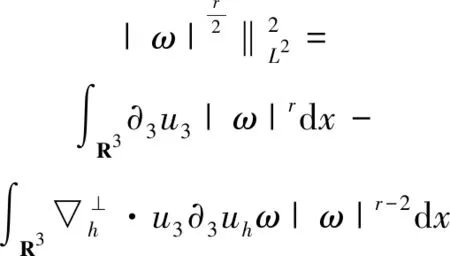
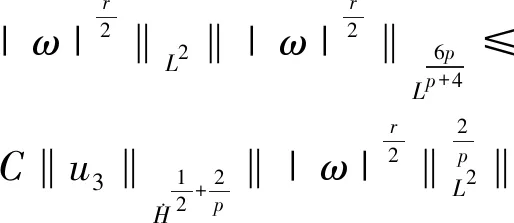





2.2 垂直方向项的估计
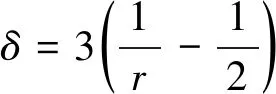
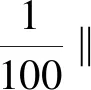

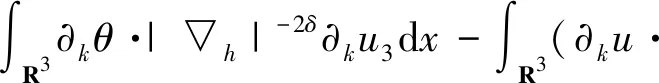
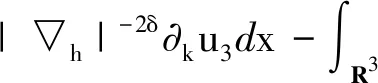



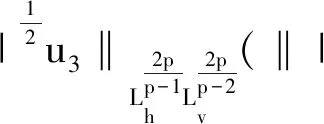

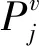



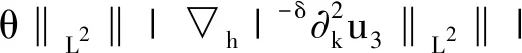
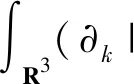
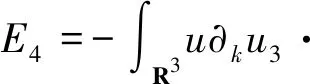


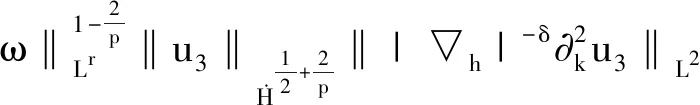
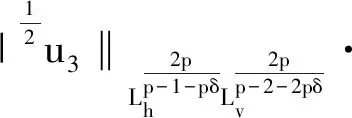
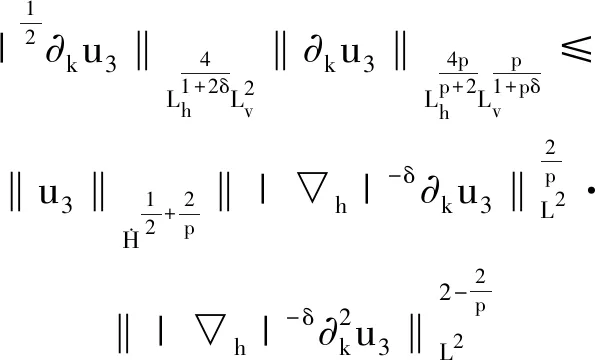


2.3 定理1的证明
