简谐与光晶格复合势阱中旋转二维玻色-爱因斯坦凝聚体中的涡旋链*

张志强

(郑州商学院,通识教育中心,郑州 451200)

利用数值计算方法,研究了由简谐势与光晶格势构成的复合势阱中旋转二维玻色-爱因斯坦凝聚体中涡旋的产生、涡旋链的形成,以及涡旋链的特性.首先利用多重网格预条件共轭梯度法,研究了二维凝聚体中涡旋的产生、涡旋链的形成及分布情况和不同物理参量对涡旋链的影响;其次利用时间分裂谱方法研究了涡旋链随时间的演化情况.结果表明,囚禁于复合势阱的凝聚体中涡旋的产生,对应于势阱的极小值,当光晶格深度增大到一定值时,凝聚体中形成了涡旋链,而随着光晶格深度的进一步增大,凝聚体中涡旋链中的涡旋深度不断减小,最终涡旋链完全消失.当原子间相互作用强度增大,凝聚体的分布范围扩大,凝聚体中的涡旋和涡旋链的数量也增加,但当原子间相互作用强度增大一定值后,涡旋链的对称性被破坏.随着凝聚体旋转角速度的增大,凝聚体的分布范围随之扩展,凝聚体中涡旋和涡旋链的数量也随之增加.当凝聚体旋转角速度接近外部势阱的谐振频率时,涡旋链的直线排列被破坏.还发现凝聚体中涡旋链随时间演化存在3 个阶段:第1 阶段涡旋链与凝聚体一同旋转且保持原有的链状分布不变;第2 阶段出现了涡旋空间挤压现象,涡旋链被破坏;第3 阶段出现了涡旋空间扩张现象,最终涡旋链消失.

1 引言

自从1995 年在实验中首次实现玻色-爱因斯坦凝聚(BEC)以来[1−3],由于其特有的可操控性,使其成为一个全新的量子模拟和研究相互作用量子体系的理想平台.BEC 中具有丰富的非线性现象,如亮孤子及暗孤子[4,5]、涡旋及涡旋对[6−8]和涡旋面[9]、怪波[10,11]等,成为物理学发展最迅速、成果最丰富的领域之一,受到了广泛的关注和持续的研究.

BEC 本质上是一种宏观量子效应,其具有量子波动性、宏观量子相干性和人工可调控性.与其他非线性系统相比,BEC 具有更多的可调控的物理参量,如原子间相互作用强度[12]、囚禁凝聚体的外部势阱、自旋-轨道耦合作用[13]、凝聚体旋转频率[14]等.

实验上,基于Feshbach 共振技术[15],可以调节BEC 中原子的S-波散射长度的大小甚至正负.S-波散射长度的变化会改变原子间相互作用强度,对BEC的物性有重要影响.实验通过一个随时间变化的外加磁场[16],不仅可以调节S-波散射长度的大小随时间线性变化、指数变化和周期性变化等,还可以调节原子间相互作用从排斥到吸引,从而在BEC 中观察亮孤子的形成.Nguyen等[17]利用Feshbach 共振技术快速地将BEC 中原子间相互作用从排斥调节到吸引,基于调制不稳定性在BEC 中观察到了亮孤子阵列的形成,并且孤子之间呈相互排斥作用.2020年,Di Carli等[18]利用Feshbach 共振技术加上一个空间梯度磁场,实现了长时间存在的BEC,并且其中一部分区域中的BEC 原子间为排斥相互作用、另一部分BEC 原子间相互作用为相互吸引.他们首次在实验中研究了非均匀BEC的动力学行为,并且还观察了孤子的形成,以及孤子从相互吸引作用区域隧穿到相互排斥作用区域的动力学行为.2009年,美国国家标准技术研究所联合量子中心的Spielman 课题组[19]在实验中采用两束Raman 光耦合原子的Zeeman内态成功实现了人造规范矢势,随后,他们又相继实现了人造均匀规范势和自旋-轨道耦合等等.针对自旋-轨道耦合BEC的基态和非线性物质波等的研究中,在自旋-轨道耦合BEC 观察到了Hess-Fairbank 效应和拓扑涡旋量子态[20],发现了平面波态、条纹态、分数Skyrmion 涡旋态、Majoranan孤子、拓扑超流态等新奇量子现象[21−23].

理论上,Gligorić等[24]研究了BEC 中的离散亮孤子,发现当原子间相互作用增大到一定值时,离散亮孤子在晶格中可保持稳定.考虑高斯分布形式的原子间相互作用,Balaž等[25]发现在雪茄型非均匀BEC 中也会产生法拉第波.BEC 中的孤子通过线性势时,随空间坐标变化的原子间相互作用会增强孤子的隧穿.当化学势超过临界值时,Sudharsan等[26]发现在二维BEC 中可形成稳定涡旋.Kengne等[27]研究了BEC 中平面波的调制不稳定性,并详细介绍了如何通过原子间相互作用和外部势阱来精确操控BEC 中的孤子.通过使用直接数值模拟和变分法,Cheng等[28]研究了双色光晶格势阱中BEC的静态和动力学性质,证实随坐标空间变化的原子间相互作用的正负和大小对BEC的性质有重要影响.考虑周期性的原子间相互作用,Wang等[29]发现暗孤子稳定性与BEC 背景形成的周期性结构密切相关.北京信息科技大学Wang等[30]研究了一维、二维和旋转BEC,发现在一维和二维BEC 中都存在稳定的局域非线性物质波,如呼吸孤子和移动的孤子等,而在旋转BEC 中存在量子化涡旋.中科院数学与系统研究院Yan等[31]发现二维BEC 中也存在稳定的超流态.

基于BEC的组分、几何维度、外部囚禁势和原子相互作用强度等参数的高度可控性,既可利用该平台研究BEC 中的物质波干涉、孤子、量子液滴、集体激发、涡旋等基础物理,也可以模拟Hubbard 模型、Su-Schrieffer-Heeger 模型等量子体系,探索其中的新奇量子现象.

综上所述,本文考虑了一个由二维谐振势与一维光晶格势组成的复合势阱,旋转二维玻色-爱因斯坦凝聚体囚禁在复合势阱中,研究了二维凝聚体中涡旋的产生、涡旋链的形成及分布情况以及涡旋链随时间的演化情况.首先得到了描述复合势阱中旋转二维BEC 体系的无量纲Gross-Pitaevskii(GP)方程,其次介绍了数值计算方法,并由实际实验数据,选取了计算参数和凝聚体初始条件.由计算结果,分别讨论了涡旋及涡旋链的形成、光晶格深度、原子间相互作用强度、凝聚体旋转角速度对涡旋链的影响,最后,研究了涡旋链随时间演化情况.

2 理论模型及数值计算

2.1 理论模型

旋转二维玻色-爱因斯坦凝聚体可由二维Gross-Pitaevskii(GP)方程描述:

V(X,Y)为二维外部势阱,选取二维谐振势与一维光晶格势组成的复合势阱,形式如下:

其中,ωX和ωY表示二维谐振势阱X和Y方向的谐振频率,E0表示光晶格的深度,D=λL/2 表示光晶格的间距,这里的λL为激光的波长.

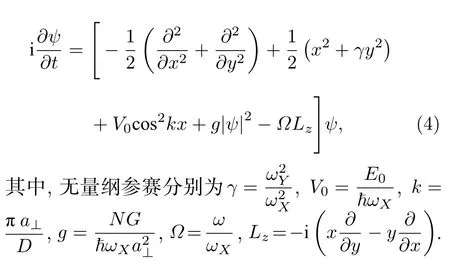
2.2 数值计算方法与参数选取

方程(4)的解析解是不容易得到的,因此,通常选择一种合适的数值计算方法,可以较为方便得到方程(4)的数值解.本文选择多重网格预条件共轭梯度法[32](multigrid preconditioned conjugate gradient method).该方法在文献[32]中有详细的介绍,是一种高效的求解旋转BEC 波函数密度分布的数值方法.为此,选取一个正方向区域U=[−L,L]2,将正方向区域在两个方向都等分成M份,间隔为hx=hy=2L/M.在本文的计算过程中,取L=10,通常M取一个较大的正整数,为了达到更好的精度和较快的计算速度,在计算程序中,取M=210.

根据Williams等[33]的实验数据,考虑玻色-爱因斯坦凝聚体由87Rb 原子组成,选取的数值计算参数如下:总原子数目N=1.5×104,谐振势阱的谐振频率ωX=ωY=2π×20.1 Hz,S-波散射长度as=5.61nm.这样,无量纲化后的单位长度对应的实际长度是2.40 μ m,无量纲单位时间对应的实际时间是7.9 ms.依据上述实验中的参数,其他数值计算参数选取为:k=1.25,g=0.1,Ω=0.7.后续,可以通过改变g或者Ω值,讨论原子间相互作用强度及凝聚体旋转角速度对凝聚体中涡旋链的影响.

在本文的计算过程中,选取的凝聚体初始条件为归一化的二维高斯波包,形式如下:

3 结果与讨论

3.1 谐振势与光晶格势构成的复合势阱中涡旋链的形成

首先,讨论光晶格势对涡旋链形成的影响.图1给出了不同光晶格深度时凝聚体的密度分布|ψ(x,y)|2的图像.图1(a)对应于光晶格深度为0,也就是对应于只有谐振势阱的情况.此时,凝聚体分布呈现中间高,四周逐渐降低,这是典型的二维高斯型孤子密度分布.在二维谐振势阱中,凝聚体密度分布的本征态就对应于二维高斯型孤子[34].从图1(a)还可以看到,此时凝聚体中并没有涡旋存在.当设置光晶格深度V0=0.05时,对应的凝聚体密度分布图像如图1(b)所示.此时,凝聚体中出现了涡旋,并且涡旋的分布呈现水平方向(x方向)和竖直方向(y方向)大致对称的排列.分析认为,凝聚体中涡旋产生的原因是,涡旋对应于空间中总能量的局部最小值,仅考虑外部势阱时,就要求外部势阱存在一个极小值.否则,即使凝聚体旋转得足够快,涡旋也不会形成[9].由于此时光晶格的深度很小,外部势阱仍然由谐振势阱占主导地位,这就使得涡旋的分布在空间上呈现x和y方向大致的对称性.增大光晶格深度至V0=0.5时,如图1(c)所示,凝聚体中涡旋排列的对称性分布就被破坏,此时涡旋的分布不再具有对称性.当继续增大光晶格深度V0=1.5时,凝聚体中涡旋开始出现竖直方向(y方向)上的链式排布,如图1(d)所示.可以认为,此时凝聚体中形成了涡旋链,在竖直方向(y方向)上,出现了5 条可分辨的涡旋链.随着光晶格深度继续增大,如图1(e)和(f)所示,涡旋链更加清晰可辨,而且随着光晶格深度的增大,凝聚体的分布出现了明显的条带状分布.这是由于光晶格深度的增大,其囚禁凝聚体的能力增强,导致凝聚体分布在光晶格的最小值处,从而出现了条带状的凝聚体密度分布.涡旋链的形成,主要是x方向光晶格势阱的作用,由于光晶格深度的增大,其囚禁凝聚体的能力增强,导致凝聚体分布在光晶格的最小值处,从而出现了y方向上条带状的凝聚体密度分布.涡旋分布在条带状的凝聚体之间,进而形成了沿y方向的涡旋链.光晶格深度越深,条带状分布就越明显.

图1 不同光晶格深度对涡旋链形成的影响(a);(b);(c);(d);(e);(f).其他参数设置为:,,V0=0 V0=0.05 V0=0.5 V0=1.5 V0=3.0 V0=4.5 k=1.25 g=0.1 Ω=0.7 V0=0 V0=0.05 V0=0.5 V0=1.5 V0=3.0 V0=4.5 k=1.25 g=0.1Ω=0.7Fig.1.Effect of the depth of the optical lattice on the formation of vortex chains:(a);(b);(c);(d);(e);(f).Values of other parameters are,,and.

3.2 光晶格深度对涡旋链的影响

通过关于涡旋链的讨论,发现光晶格深度对涡旋链分布和形态有影响,因此,重点讨论光晶格深度对涡旋链的影响.如图2 所示,给出了不同光晶格深度的情况下凝聚体的密度分布|ψ(x,y)|2的图像.对比图2(a)—(c),发现凝聚体里均产生了5 条涡旋链,随着光晶格深度的增大,例如光晶格深度V0=3.0增大到9.0,凝聚体的条带状分布愈发明显.可见随着光晶格深度的进一步增大,其囚禁能力也进一步增强,凝聚体越来越多的分布在光晶格的最小值处,从而凝聚体的条带状密度分布就越明显.进一步增大光晶格深度到V0=15.0,图2(d)给出了此时凝聚体的密度分布,从图2(d)可以看到,凝聚体中形成了6 条带状结构,中间仍然出现了5 条涡旋链,不过最外侧的两条涡旋链只能勉强分辨清楚.对比图2(a)—(d),可以看出,随着光晶格深度的增大,最外侧的涡旋链中的涡旋深度在不断减小,到图2(d)所示情况时,这两条涡旋链中的涡旋处于消失的边缘.当光晶格深度增加至V0=21.0,凝聚体的密度分布如图2(e)所示.此时,凝聚体仍然呈6 条带状结构,中间只出现了3 条涡旋链,最外侧的涡旋链已经完全消失.继续增大加光晶格深度V0=30.0,如图2(f)所示,凝聚体中的涡旋基本上消失至不可见状态,凝聚体只剩下6 条带状密度分布,可以得出涡旋链已经消失.综合上述,光晶格深度对涡旋链的形成和演化有重要影响,随着光晶格深度的增大,凝聚体中最外侧涡旋链中的涡旋深度不断减小,最终消失.进一步增大光晶格深度,内测涡旋链中的涡旋深度也减小,最终所有的涡旋链完全消失,凝聚体只剩下条带状的密度分布.

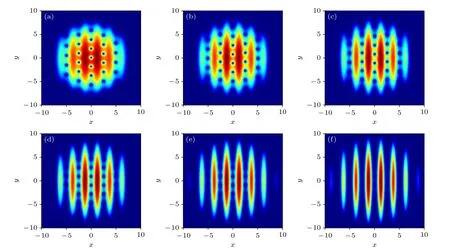
图2 不同光晶格深度情况下,凝聚体的密度分布 |ψ(x,y)|2的图像(a)V0=3.0;(b)V0=6.0;(c)V0=9.0;(d)V0=15.0;(e)V0=21.0;(f)V0=30.0.其他参数与图 1 中的相同Fig.2.The density distribution of BEC at different optical lattice depths:(a)V0=3.0;(b)V0=6.0;(c)V0=9.0;(d)V0=15.0;(e)V0=21.0;(f)V0=30.0.The other parameters used are the same as those in Fig.1.

随着光晶格深度的增大,光晶格势阱囚禁能力增强,凝聚体分布越来越集中在光晶格的最小值处,导致条带状的凝聚体密度分布越来越明显.涡旋链分布在条带状的凝聚体之间,随着光晶格深度越深,条带状分布就越明显,条带状凝聚体之间部分的涡旋深度就越来小,最终,条带状之间几乎不存在凝聚体分布,涡旋和涡旋链就随之消失.

3.3 原子间相互作用强度对涡旋链的影响

在BEC的相关实验中,广泛应用了Feshbach共振技术来改变BEC 组成的原子间相关作用强度,用以调控BEC 中的亮孤子的产生,或者调节BEC 中孤子的性质.Feshbach 共振技术使原子间相互作用强度成为一个可以方便调节的宏观物理量,因此,本节讨论原子间相互作用强度的改变,对BEC 中涡旋链的影响情况.图3 展示了不同原子间相互作用强度情况下凝聚体的密度分布|ψ(x,y)|2的图像,从图3(a)—(f),原子间相互作用强度从g=0.05 增大到g=0.90.

图3 不同原子间相 互作用强度情况下,凝聚体的密度分布|ψ(x,y)|2的图像(a)g=0.05;(b)g=0.10;(c)g=0.15;(d)g=0.30;(e)g=0.60;(f)g=0.90.其他参数设置为:k=1.25,V0=3.0,Ω=0.7Fig.3.De nsity distribution of BEC for different interaction strengths between atoms:(a)g=0.05;(b)g=0.10;(c)g=0.15;(d)g=0.30;(e)g=0.60;(f)g=0.90.Values of other parameters are k=1.25,V0=3.0,and Ω=0.7.

首先,可以直观发现,随着原子间相互作用强度的增大,BEC的分布范围随之扩大,这是由于原子间相互作用强度大于0时,表示原子间是相互排斥的,随着相互作用强度的增大,原子间排斥作用增大,就导致了BEC 原子分布的范围扩大.

其次,除了BEC 分布范围扩大,原子间相互作用强度还对涡旋链的长度和涡旋链中涡旋数目有重要影响.当g=0.05时,如图3(a)所示,此时成型的涡旋链有3条,这3 条涡旋链中的涡旋也只有4 个.研究发现在凝聚体的边缘,还有一些涡旋正在形成.随着原子间相互作用强度增大到g=0.10,BEC 中形成了5 条涡旋链,每条涡旋链中至少有4 个涡旋,居于中间的涡旋链中出现了7 个涡旋,如图3(b)所示,此时,凝聚体中的涡旋数量也随着原子间相互作用强度的增大而增加.继续增大原子间相互作用强度至g=0.15,从图3(c)中可以看到,这时凝聚体中仍然是5 条涡旋链,但每条涡旋链的涡旋数量比之前有所增加,凝聚体中总的涡旋数目更多了.当设置原子间相互作用强度g=0.30,BEC 中出现了7 条涡旋链,如图3(d)所示,每条涡旋链中的涡旋数目5—9 个不等,凝聚体中的涡旋数目继续增多.进一步增大原子间相互作用强度g=0.60,凝聚体中仍旧维持7 条涡旋链,每条涡旋链中的涡旋数目增到8—10个,BEC 中涡旋的总数目也进一步增大,见图3(e).此外,中间3 条涡旋链中的涡旋排列,出现了不在一条直线上的情况,也就是说,随着原子间相互作用强度进一步增大,凝聚体中的涡旋链的对称性被破坏.继续增大原子间相互作用强度g=0.90,从图3(f)中可以发现,凝聚体中的涡旋数量继续增加,中央涡旋链的涡旋排列出现了更多的不规则排列,也就是涡旋链的对称性出现了更多的破坏.

分析认为,凝聚体分布范围的扩展,是由于原子间排斥性相互作用强度的增大导致的.而涡旋对应于空间中总能量的局部最小值,为了保持凝聚体能量的最小值,随着原子间排斥性相互作用强度的增大,凝聚体中涡旋的数目也随之增加,大量的涡旋在y方向上排列在凝聚体中,从而来降低系统的总能量[35],最终达到一个稳定的状态,此时呈现出的就是涡旋链数目增加、每条涡旋链中涡旋数目也增加.

综上所述,随着原子间相互作用强度的增大,BEC的分布范围随之扩大,凝聚体中的涡旋和涡旋链的数量也随之增加,当原子间相互作用强度增大一定值后,涡旋链的对称性出现破坏,涡旋的排列不再对称排列.可见,原子间相互作用强度对凝聚体中的涡旋和涡旋链有重要影响,通过Feshbach共振技术调节原子间相互作用强度,可以有效的调控凝聚体中的涡旋的数量和涡旋链的形态.

3.4 凝聚体旋转角速度对涡旋链的影响

通过设置不同的凝聚体旋转角速度Ω的值,讨论旋转角速度对凝聚体中涡旋链的影响.图4 给出了不同凝聚体旋转角速度Ω时凝聚体的密度分布|ψ(x,y)|2中的涡旋及涡旋链的分布情况.当凝聚体旋转角速度较小,凝聚体中没有出现涡旋,如图4(a)所示,此时设置Ω=0.1,凝聚体呈现对称性分布,其中没有涡旋存在.当设置凝聚体旋转角速度Ω=0.3时,凝聚体中出现了4 个涡旋,呈对称分布在凝聚体中,如图4(b)所示,此时还不能称之为形成了涡旋链.当增大凝聚体旋转角速度至Ω=0.5,此时凝聚体中出现了14 个涡旋,凝聚体中的涡旋排列形成了3 条较为明显的纵向有序结构,这时可以认为凝聚体中形成了涡旋链,如图4(c)所示.继续增大凝聚体旋转角速度到Ω=0.7,从图4(d)中可以看出凝聚体中涡旋数量大大增加,总共出现了27 个涡旋,同时涡旋链也增加到5条,每条涡旋链里的涡旋数目也增多,这说明随着凝聚体旋转角速度的增大,涡旋和涡旋链的数量都随之增多.进一步增大凝聚体旋转角速度Ω=0.9,此时凝聚体中出现了64 个涡旋,凝聚体中涡旋的数量大幅增加,还形成了7 条涡旋链,每条涡旋链中涡旋的数量也随之增加,如图4(e)所示.最后设置凝聚体旋转角速度Ω=0.95,这时凝聚体旋转角速度接近囚禁凝聚体的谐振势阱的谐振频率,这种情况称为最低朗道能级近似(the lowest Landau level approximation)[36,37].此时凝聚体的分布如图4(f)所示,可以看到,凝聚体中产生了更多的涡旋,共生成了84 个涡旋,涡旋几乎占据了凝聚体的每个地方,这时的7 条涡旋链每条中至少有10 个涡旋,中央的涡旋链有14 个涡旋.中央涡旋链两侧的涡旋链,涡旋的分布出现了不在一条直线上的情况,这说明,凝聚体的高速旋转,破坏了涡旋的对称性分布.

对比图4 中对应于凝聚体旋转角速度不同的6 幅图像,可以发现随着凝聚体旋转角速度的增大,凝聚体的分布范围也随之扩展,特别是当旋转角速度趋近于1时,凝聚体几乎占据了整个正方向区域U=[−10,10]2.随着凝聚体旋转角速度的增大,凝聚体中的原子由于离心力的增大,进一步远离原子云的中心区域,造成凝聚体分布范围扩大,但由于外部势阱的在x方向的周期性分布,凝聚体的分布仍然呈现一定的周期性分布,在旋转角速度较小时,凝聚体中涡旋和涡旋链基本上呈现关于中央的轴对称性分布,在旋转角速度接近外部势阱的谐振频率时,即最低朗道能级近似时,对称性出现了少许的破坏,涡旋不再呈现直线排列.这是由于随着凝聚体旋转角速度的增大,较高的旋转角速度减小了外部势阱的限制作用,二者共同作用下,就导致涡旋数目增加,也导致了涡旋链不再呈直线排列.

图4 不同旋转角速度情况下,凝聚体的密度分布 |ψ(x,y)|2 中的涡旋及涡 旋链的分布情况(a)Ω=0.1;(b)Ω=0.3;(c)Ω=0.5;(d)Ω=0.7;(e)Ω=0.9;(f)Ω=0.95.其他参 数设置为:k=1.25,g=0.1,V0=3.0Fig.4.Distribution of vortices and vortex chains in the BEC under different rotation frequency:(a)Ω=0.1;(b)Ω=0.3;(c)Ω=0.5;(d)Ω=0.7;(e)Ω=0.9;(f)Ω=0.95.Values of other parameters are k=1.25,g=0.1,and V0=3.0.

3.5 涡旋链随时间演化

利用时间分裂谱方法(time-splitting spectral metho d)[38,39],研究涡旋链随时间的演化情况.为研究涡旋链随时间的演化情况,选取计算参数k=1.25,g=0.1,V0=3.0,Ω=0.7 时BEC 中形成的涡旋链分布为初始计算条件,对应的凝聚体密度分布|ψ(x,y)|2如图5(a)所示.此时,凝聚体中的涡旋在竖直方向(y方向)上的出现了明显链式排布,形成了涡旋链,且涡旋链排列整齐、清晰可辨,而凝聚体的分布刚刚出现条带状分布.以此为初始状态研究涡旋链的演化,不失一般性可以作为一个有代表性的涡旋链随时间的演化情形.

为了在较长的时间范围内有较高的计算精度,计算过程中时间步长取一个较小的值,为∆t=0.0001.计算了从t=0到t=16.0 这一段时间的凝聚体演化情况,结果如图5所示.图5 中的(a)—(f),从t=0至t=5.0,间隔1 个无量纲时间单位给出一幅图像;(g)—(l),从t=6.0 开始至t=16.0,间隔2 个无量纲时间单位给出一幅图像.

对比t=0至t=4.0的图像,可以发现,随着时间的延长,凝聚体沿顺时针方向旋转,凝聚体中的涡旋和涡旋链数量没有变化,涡旋链仍呈直线排列,不过涡旋链的排列方向沿顺时针方向旋转,凝聚体外侧涡旋的位置也沿顺时针方向发生了移动,但位移变化量不大.随着时间的延长,凝聚体边缘的原子,出现了絮状分布,意味着这些原子在离心力的作用下,远离了凝聚体主体部分,换句话说旋转凝聚体中的原子数目会随着时间延长而减少.

值得注意的是,对比t=4.0,5.0,6.0和8.0 时刻凝聚体密度分布图像,即图5(e)—(h),凝聚体中的涡旋链似乎旋转方向发生了反转,好像是沿着逆时针方向旋转一样.为了更清晰展示凝聚体随时间的演化,以更小的时间间隔对t=4.0到t=6.0 之间凝聚体的演化情况进行精细分析.分析结果是,凝聚体中的涡旋和涡旋链仍然是沿着顺时针方向旋转,但在旋转过程中,凝聚体中间部分的涡旋随着时间的推移,涡旋之间的距离变小,呈现一种涡旋空间挤压的现象.在文献[40]中,一种同时发生在凝聚态涡旋结构和原子云形状的类似现象被称为“几何压缩”(geometric squeezing)[40].分析认为,这种空间挤压现象产生的原因是凝聚体中的涡旋,在随着凝聚体顺时针旋转时,由于外部势阱的限制作用,导致涡旋的运动轨迹并不是圆弧,而是出现了朝圆心方向运动,最终形成涡旋在空间挤压的现象.

图5 旋转BEC 中涡旋和涡旋 链随时间演化(a);(b);(c);(d);(e);(f);(g);(h);(i);(j);(k);(l).其他参数为,,,t=0 t=1.0 t=2.0 t=3.0 t=4.0 t=5.0 t=6.0 t=8.0 t=10.0 t=12.0 t=14.0 t=16.0 k=1.25 g=0.1 V0=3.0Ω=0.7Fig.5.Evolution of vortices and vortex chains of the rotating BEC:(a);(b);(c);(d);(e);(f);(g);(h);(i);(j);(k);(l).Values of other parameters are t=0 t=1.0 t=2.0 t=3.0 t=4.0 t=5.0 t=6.0 t=8.0 t=10.0 t=12.0 t=14.0 t=16.0 k=1.25 g=0.1 V0=3.0 Ω=0.7,,,and.

而在t=8.0 之后,如图5(i)—(l)所示,随着时间的推移,涡旋不再有呈现直线排列的规律,可以认为凝聚体中的涡旋链逐渐消失.值得注意的是,这段时间内,涡旋朝向凝聚体的外侧运动,凝聚体中央的涡旋数目随着时间延长而减少.凝聚体中的涡旋之间的距离开始随着时间推移而逐渐变大,这与t=4.0到t=8.0 之间涡旋的运动情况相反.该阶段可以称为涡旋空间扩张.这种情况产生的可能原因是旋转BEC 中的涡旋在离心力的作用下,均有向凝聚体外侧运动的趋势,随着时间的延长,导致涡旋间的距离随着时间的推移而增大,涡旋间距离逐渐扩大,最终出现了涡旋空间扩张这种现象.

通过以上分析,发现了涡旋链随时间演化存在3 个阶段:第1 阶段,涡旋链随着凝聚体旋转且保持原有的链状分布不变;第2 阶段,旋转BEC中涡旋出现了空间挤压现象,涡旋链被破坏;第3 阶段,出现了涡旋空间扩张,涡旋链消失.

为了从实验上实现涡旋链及研究其随时间的演化情况,建议采取如下的实验参数.考虑由单一组分的87Rb 所构成的BEC 系统,原子数目约为N=1.5×104个[33].首先将其装载到一个由磁场产生碟形谐振势阱中,谐振势阱的频率可取为ωX=ωY=2π×20.1 Hz,ωZ=2π×53.0 Hz[33].凝聚体的旋转可以通过称为“旋转框架”的方式产生,即在谐振势阱上叠加一个旋转频率为ω=Ω×ωX的激光束.之后,利用两束激光相干的方法,产生一维的光晶格势阱,光晶格势阱的深度可以通过调节激光强度或者两束激光的相干角而改变.当凝聚体中形成了稳定的涡旋链之后,可以让其自由演化,研究其随时间的演化情况.凝聚体中涡旋和涡旋链的动力学特性可以通过实时成像(the real-time imaging)来观察.

4 结论

综上所述,考虑囚禁在二维谐振势与一维光晶格势组成的复合势阱中的旋转二维玻色-爱因斯坦凝聚体,研究了凝聚体中涡旋及涡旋链的分布情况,以及涡旋链随时间的演化.首先,理论上得到描述其波函数概论密度分布的无量纲的二维GP方程.其次,通过多重网格预条件共轭梯度法,采用数值方法研究了光晶格势阱中涡旋及涡旋链的产生,光晶格势阱深度、原子间相互作用强度和凝聚体旋转角速度对涡旋链的影响.结果表明,凝聚体中涡旋对应于外部势阱的一个极小值,光晶格势阱深度增大到一定值时,凝聚体中形成了涡旋链.随着光晶格势阱深度的进一步增大,凝聚体中涡旋链中的涡旋深度不断减小,最终所有的涡旋链完全消失,只剩下条带状的密度分布.随着原子间相互作用强度的增大,凝聚体的分布范围随之扩大,凝聚体中的涡旋和涡旋链的数量也随之增加,当原子间相互作用强度增大一定值后,涡旋链的对称性出现破坏,涡旋的排列不再对称排列.随着凝聚体旋转角速度的增大,凝聚体的分布范围也随之扩展,凝聚体中涡旋和涡旋链的数量也随之增加,在旋转角速度较小时,凝聚体中涡旋和涡旋链基本上呈现关于中央的轴对称性分布,在旋转角速度接近外部势阱的谐振频率时,即最低朗道能级近似时,对称性出现了少许的破坏.最后,探讨了涡旋链随时间的演化情况.发现了涡旋链随时间演化存在3 个阶段:第1 阶段涡旋链与凝聚体一同旋转且保持原有的链状分布不变;第2 阶段出现了涡旋空间挤压现象,涡旋链被破坏;第3 阶段出现了涡旋空间扩张,涡旋链消失.

上述结果表明,光晶格势阱深度、原子间相互作用强度和凝聚体旋转角速度对凝聚体中的涡旋和涡旋链有重要影响,通过调节相关物理量的大小,可以有效调控凝聚体中的涡旋的数量和涡旋链的形态,为将来的实验与应用提供一定的理论参考和指导.