妙用圆锥曲线的统一方程

程德明

(安徽省阜阳市第五中学 236000)

一、圆锥曲线的诞生及发展

圆锥曲线最早是由古希腊学者梅内克谬斯(Menaechmus)进行系统研究的，他用顶角分别为直角、锐角和钝角，三种直圆锥以不过顶点而垂直一条母线的平面截割这三种圆锥曲面，而分别得到抛物线、椭圆和双曲线的一支.

设圆锥的半顶角为α，平面与圆锥的轴所成的角为θ：

当θ=α时，截面和圆锥的一条母线平行，交线是抛物线；

当α<θ≤π/2 时，截面和所有的母线相交，交线是椭圆，特别当θ=π/2 时，交线时圆；

当 0≤θ<α时，截面和两条母线平行，交线时双曲线.

因此，圆锥曲线包括抛物线、椭圆和双曲线，统称圆锥曲线.

随着社会的不断发展，科学的不断进步，到了亚历山大里亚时期，阿波罗尼奥斯在他的《圆锥曲线学》中指出同一圆锥的不同截口曲线可以是抛物线、椭圆和双曲线，并且研究了圆锥曲线的共轭直径、切线和法线及其性质.这就让圆锥曲线不断的发展起来，并逐渐的应用起来直到现在.在高考的数学当中，圆锥曲线问题也是一个每年必考的题型，所以人们对圆锥曲线这个问题也越来越重视并进行多次研究.

二、圆锥曲线的统一性

圆锥曲线的统一性包括统一定义、统一公式和统一方程.从双曲线和椭圆来看，二者有许多相似的地方和相同的特性.例如，它们都有离心率和焦半径、切线方程、焦点三角形、焦准距和通径，而且他们这些特性的表达式都是十分相似的，它们的原理也是相同的.只是因为它们的图形不一样，所以他们有了一些微小的差别.也正是因为他们有这样多的详细的性质，所以考试时会在圆锥曲线当中也衍变出许多的问题，而且这些问题又可以与其他的知识点相结合，所以这也成了热门的考试题型之一的原因.

其中他们的统一性的应用最常见的是中点弦的求解问题.中点弦方程的求解方法有以下几种.

1.联立方程法

一般这样的题型中会在已知条件中告诉我们截锥曲线的方程和与这条弦有关的条件.我们可以利用点斜式设出该弦的方程.然后将这个方程与圆锥曲线方程联立.然后消去一个未知数，由韦达定理得到两根之和的表达式，再由中点坐标公式和两根之和的具体数值，求出该弦的方程.

2.点差法(代点相减法)

我们都知道弦一定与圆锥曲线图形有两个交点，我们一般也叫作为弦的两端点.设出弦的两端点坐标(x1,y1)和(x2,y2)，代入圆锥曲线的方程，然后二者相减，将会得到一个弦中点与斜率有关的方程，这种方法大大地减少了我们的计算量，我们把它叫作点差法或者是代点相减法.

三、妙用圆锥曲线的统一方程

圆锥曲线的统一方程的性质不只用在求解中点弦时，更多的是利用它的性质与其他知识相结合的题.下面就总结一下妙用圆锥曲线的统一方程的题型.

1.求圆锥曲线的离心率及离心率的取值范围

在解决这类型问题时，最简单的方法就是直接用定义，而在大多数的题型中，并没有直接给到我们所需要的a和c的值.所以我们会选择用更多其他的方法来解出a和c的值或者是与a和c有关的关系式.其次就是可以根据直线与圆锥曲线的位置为背景，设而不求确定e的方程.在求解的e的取值范围时，我们更多的是去构造不等式来确定e的取值范围.还有一种方法就是利用数形结合的方法确定a与c有关的不等式，这种办法可以直接从图上观察到一些特点，可以让学生有更好的思路去解题.下面通过一个例题来看如何求圆锥曲线的离心率及离心率的取值范围.

2.求圆锥曲线上点的坐标

求圆锥曲线上点的坐标一般用的是联立方程的方法.我们都知道圆锥曲线与直线的位置关系结果就是可能有一个交点，或者是两个交点，或者没有交点.所以当联立一个方程组之后，会得到一个方程式.我们可以根据方程式去求Δ的值，比较它和零的大小，若是大于0，则说明有个不同的交点;如果是等于0说明有一个交点;小于0的时候，就没有交点.然后再通过韦达定理进行进一步的计算.下面通过一个简单的例题来求圆锥曲线上的一个点.

(1)求点P的坐标;

(2)设M是椭圆长轴AB上的一点，M到直线AP的距离等于|MB|，求椭圆上的点到点M的距离d的最小值.

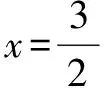
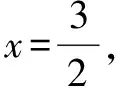
3.求最值

求最值的问题一般是出现在大题当中，最后的压轴题当中.在求解最值时，也会用到联立方程组的方法，找到交点，然后再结合题中的其他条件.而最值最常见的是与抛物线相结合，我们都知道抛物线有最高点与最低点的两种可能，一些圆锥曲线问题就会与抛物线相结合，它们的交点刚好就是抛物线的顶点，最后用这两种图形的特性去证明这一点就是它们的最值点.这只是其中的一种情况，还有的会在它们的弦的中点或者是1/3处等，它们的解决方法都离不开圆锥曲线的性质.

根据上一题的第二问，我们看一下在最值问题中的应用.

∵椭圆上的点(x,y)到点M的距离是d,

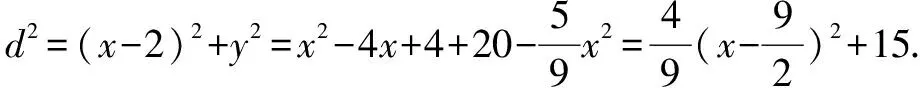
4.求距离

在圆锥曲线中求距离也是最常见的一种题型.而这个求距离一般都是运用公式.在学习圆锥曲线问题之前，我们就学习过两点之间的距离公式，还有坐标，向量它们之间的距离是怎样求的.圆锥曲线问题就可以与这些知识点相结合，考察的就是求距离问题.求距离也是利用圆锥曲线与其他图形相结合的性质来解决，尤其是一些函数的联立，这种题型也一般出现在大型题中.下面通过一个距离的范围例题来解释一下圆锥曲线中距离的问题.

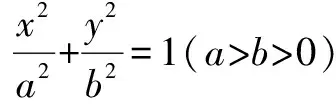
(1)求椭圆的方程;

(2)由(1)得F的坐标为(-2,0).

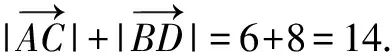
化得(3+4k2)x2+16k2x+16k2-48=0，

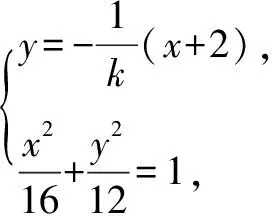
小结:圆锥曲线的图形较多，它的特点也多.其次就是圆锥曲线的知识点相对很多，而且各种图形的特点是相似的，这也就造成了同学们轻易地就混淆了它们的公式，尤其是一些正负号的记忆，如果不能够真正地从理论上去理解这个知识点，那么对圆锥曲线的记忆是有一些困难的.出题者也会因为圆锥曲线的性质多，与其他知识点结合的多样性而热衷于去出更多的圆锥曲线有关的问题去考查学生.但是如果能够真正掌握了圆锥曲线统一性的运用，能够灵活巧妙地去解剖一些题型，就会发现很多的题型利用的都是圆锥曲线的统一方程这一特点，所以我们在学习的过程中更应该注重对统一方程的应用.