拟造高中数学试题的方法与技巧
2019-03-27陈恒曦
陈恒曦
(广东省湛江市教育局教育研究室 524000)
考试随着教育的产生而产生.考试过程的核心环节是命题,命题的关键是拟题,由此也体现出教师命题的理论水平以及命题的实际技巧.数学拟题是指已知条件、已知条件展开的数学逻辑叙述(推理)过程,及由此得到的结论这三个要素组成完整数学意义的陈述.隐去或部分隐去真实、确定的完整数学意义陈述的构成要素,要求应答者构造完整数学意义的陈述,这种构造过程就是拟造数学题. 本文利用具体的数学试题去说明如何改编成题和编制新题,并对通过具体的数学试题去解读数学拟题的方法.
一、改编成题
通过改造成题(课本例题、习题、高考试题、中考试题、中高考模拟题、数学竞赛题)设计数学题,就是对原有题目的条件或结论进行适当的加工与改造,在成题的基础上制作新的数学题,这种方法通常称为改造成题法.改造成题法是设计数学题的一种基本方法,根据成题的不同特点,改造的具体途径也不尽相同,常用的有等价变形、横向变形、纵向变形、正逆变形等.
1.等价变形
就是在保持成题的关系结构的基础上,通过变换题目的条件、结论或题型拟出与原题等价的新题.
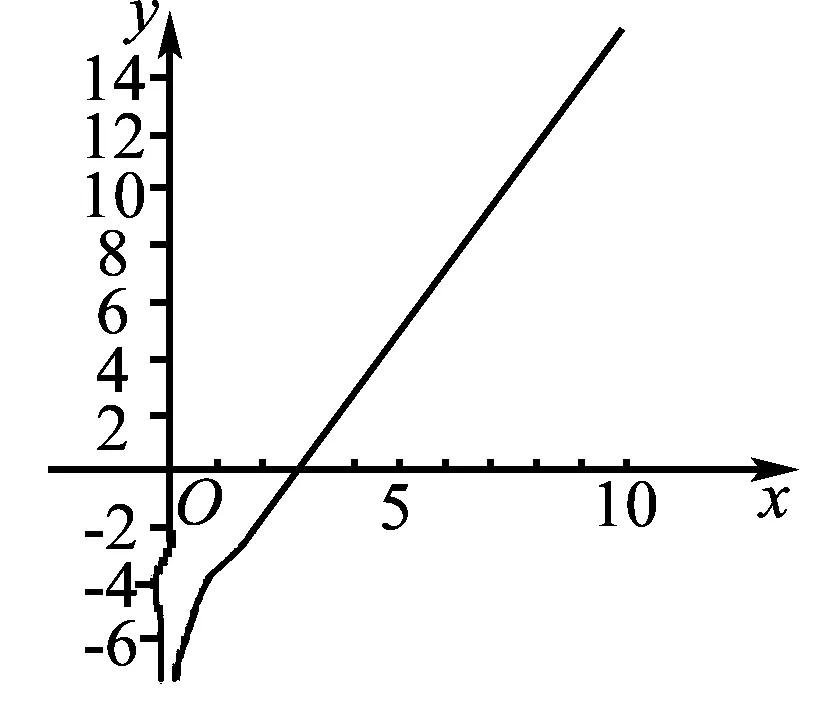
案例1 (必修1第88页例1)求函数f(x)=lnx+2x-6的零点的个数.
解析用计算器或计算机作出x,f(x)的对应值表与图像如下:

x123456789f(x)-4-1.30691.09863.38635.60947.79189.945912.079414.1972
由上表和图可知,f(2)<0,f(3)>0,则f(2)·f(3)<0,这说明函数f(x)在区间(2,3)内有零点.由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点.
本题为运用函数思想解决方程的求解问题,需要理解零点的概念(三种等价的解释).函数思想丰富了求解方程的思路,体验函数思想的作用,掌握数形结合方法.在保证原题本质不变时进行四种变换.
变式1 (2016届宁夏银川一中)已知函数f(x)的图象是连续不断的,有如下的x,f(x)的对应表则函数f(x)存在零点的区间有( ).

x123456f(x)136.1315.552-3.9210.88-52.488-232.064
A.区间[1,2]和[2,3]
B.区间[2,3]和[3,4]
C.区间[2,3]、[3,4]和[4,5]
D.区间[3,4]、[4,5]和[5,6]
变式2 (2013天津高考)函数f(x)=2x+x3-2在区间(0,1)内的零点个数是( ).
A.0 B.1 C.2 D.3
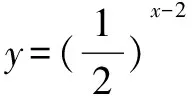
变式4 (2014山东高考)已知函数f(x)=|x-2|+1,g(x)=kx,若方程f(x)=g(x)有两个不相等的实根,则实数k的取值范围是( ).
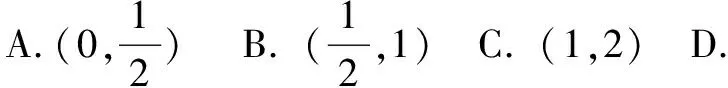
变式1通过改变条件为表格;变式2改变函数解析式;变式3改变条件形式;变式4改变问题的形式,变问题为求参数的取值范围.以上这四道改编题的本质与原题一样,就是所说的等价变形.
2.横向变形
一种方法是将几个基础题叠加在一起的方式来设计试题,简称叠加组合式.
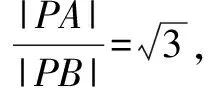
问题2 已知实数x,y满足:(x-2)2+y2=3,求y的最大值.
合成新题: 在△ABC中,a=2,b=2c,求△ABC面积的最大值.
分析问题1是一道轨迹问题(阿波罗尼斯圆),而问题2是一道有明显图形背景的最值问题.合成新题则通过一个不确定的三角形提出问题,其中顶点A到B、C的距离之比为定值.从而可先用解析法研究A的轨迹,从而求出A到边BC的距离最大 ,最终得到问题的求解.
另外一种方法,以成题为基础,利用数学各科知识的横向联系构造新题.
案例3 原题:在平面内两定点B、C的距离为a1,动点A到B、C的距离之和为2a1,求△ABC面积的最大值.
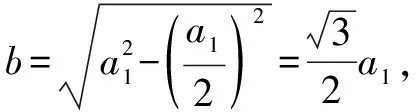
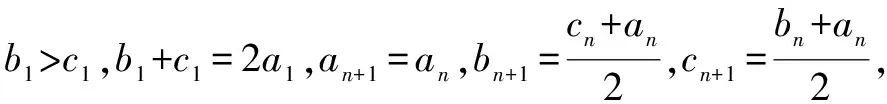
A.{Sn}为递减数列
B.{Sn}为递增数列
C.{S2n-1}为递增数列,{S2n}为递减数列
D. {S2n-1}为递减数列,{S2n}为递增数列
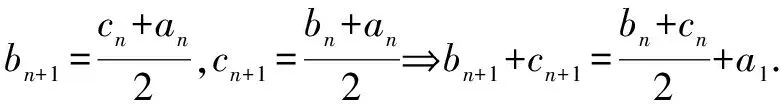
又b1+c1=2a1,
由归纳法可知bn+cn=2a1,△AnBnCn另两边之和为定值2a1,且其中bn,cn→a1,与原题当顶点为椭圆短轴顶点时达最大一致.bn,cn变化如数轴图所示:
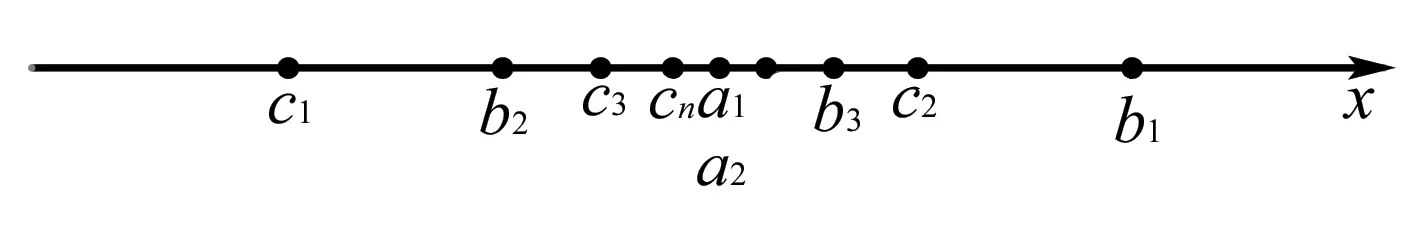
3.纵向变形
纵向变形就是递循由特殊到一般或一般到特殊的思路.对原题作特殊化、一般化的处理,通过考查题目的特殊情形在条件、结论,方法上对原题进行推广,由此来设计试题.
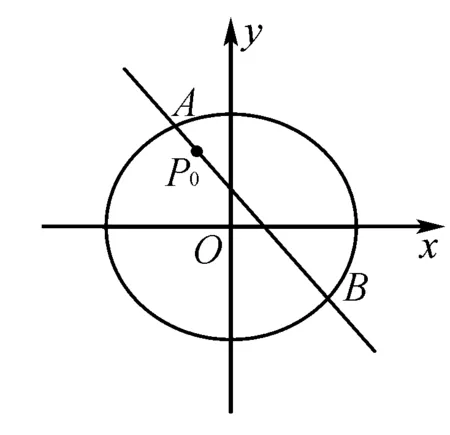
案例4 (人教版高中数学新教材必修2(A版)P133页第4题)如图,圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦.
(1)当α=135°时,求AB的长;(2)当弦AB被点P0平分时,写出直线AB的方程.

改编2:当135°≤α≤150°时,求弦长AB的取值范围;
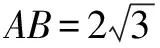
改编4:直线x-2y+5=0与圆心在原点的圆O相交于A、B两点,点P0(-1,2)平分弦AB,求圆O的方程;
案例5 (人教版高中数学新教材选修1-1(A版)P110页第7题)已知函数f(x)=x(x-c)2在x=2处有极大值,求c的值.
改编1:求函数f(x)=x(x-6)2的极大值和极小值;
改编2:已知函数f(x)=x(x-6)2在x=a处有极大值,求a的值.
改编3:已知函数f(x)=x(x-c)2在x=2处有极大值,证明:方程f(x)=6有三个解.
4.正逆变形
正逆变形,指的是将题目中的条件与结论的位置相互变换,由此来编制出新的数学题.
(1)将成题改造成给出结论,探求条件的题型
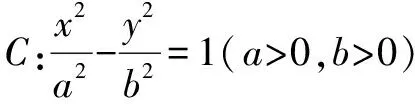
参考答案:A.
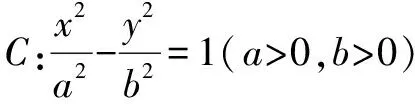
(2)将条件、结论完整的题目改造成给出条件,结论让学生猜想并进行证明的题型.
案例7 (2017年高考理数全国Ⅰ卷第12题)几位大学生响应国家的创业号召,开发了一款应用软件.为激发学习数学兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是( ).
A.440 B.330 C.220 D.110
参考答案:A
改编成已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推;整数N满足如下条件:N>100且该数列的前N项和为2的整数幂;试证明:N的最小值是440.
二、编制新题
1.利用实际问题拟造新题
通过建立数学模型,将实际问题抽象出新的数学问题.这类题的结构为:实际问题情境,数学模型化,解数学模型,从而解答这个实际问题.其目的是为了测量学生灵活运用所学数学知识分析和解决问题的能力,而解答这类题的关键,是从所学的数学知识中选取合适的数学知识,将实际问题数学化,因此,解答这类题对于培养学生的创新思维和实践能力很有实际意义.拟造这类题时,应先选定日常生活中的事实作为背景,然后用合适的数学语言来表述它.
2.利用基本量法拟造新题
在一个系统中,如果任意一个量都可由几个量导出,而这几个量又不能相互导出,则称这几个量为该系统的基本量.利用基本量法拟造数学题的思路:弄清系统的量,确定系统基本量并给予赋值,设计条件拟造题并审定计算顺序,应该指出一个系统的基本量不一定相同.例如,与等差数列{an}相应的量有a1,n,an,Sn,公差d等,而a1,d,Sn和d,n,Sn分别可作为它的基本量.利用等差数列的基本量可拟造题目:在等差数列{an}中,a6+a9+a12+a15=30,求S20.
3.利用新的数学概念、运算法则拟造新题
利用新规定的概念、法则等拟造数学题的主要步骤为:首先用数学的概念、法则等闸述新概念、法则的意义,然后用新概念、法则提出数学题.
案例8 (2009年高考四川卷) 设V是已知平面M上所有向量的集合,对于映射f:V→V,a∈V,记a的象为f(a).若映射f:V→V满足:对所有a,b∈V及任意实数λ,μ都有f(λa+μb)=λf(a)+μf(b),则f称为平面M上的线性变换,现有下列命题:
(1)设f是平面M上的线性变换,a,b∈V,则f(a+b)=f(a)+f(b);
(2)若e是平面M上的单位向量,对a∈V,设f(a)=a+e,则f是平面M上的线性变换;
(3)对a∈V,设f(a)=-a,则f是平面M上的线性变换;
(4)设f是平面M上的线性变换,a∈V,则对任意实数k均有f(ka)=kf(a).
其中的真命题是( ).(写出所有真命题的编号)
4.以高等数学知识为背景拟造新题
以高等数学的思想和知识为背景,把高等数学中的问题初等化,可以拟造新题.高等几何中有一个帕斯卡定理:“二阶曲线内接六角形的对边交点共线”.在这个定理中,把二阶曲线特殊化为圆,内接六角形用内接六边形代替,相应的对边改为对角线,则可拟造如下的题目:
已知圆的内接六边形的六个顶点分别为A(-3,4),B(0 5),C(4,3),D(4,-3),E(-3,-4),F(-5,0),求证:AD与CF的交点、BD与CE的交点、AE与BF的交点共线.
5.不完全确定条件或结论拟造新题
许多所探讨的数学题,其条件和结论都是完全确定的.但在数学教学中还经常使用结论或条件不完全确定的新题拟造方法.
案例9 (1)设△ABC的三边a,b,c满足an=bn=cn(n∈N,n≥2),试判定△ABC的类型.
(2)设等差数列{an}的前n项和为Sn,已知a1=12,S12>0,S13<0.指出S1,S2,…,S12中,哪一个值最大,并说明理由.
由这几个例题可以看出,拟造这类题需对所探求的条件或结论的范围作限制,而且这个限制表现在解答过程中需要对条件或结论进行讨论,这种类型的题属于开放型的题,对培养学生的创新思维和实践能力很有好处.
