关于电磁感应中“电容问题”的讨论
2019-03-27王成
王 成
(江苏省苏州中学 215002)
一、电容器充放电的过程的电压、电流的特点
电容充电与放电都是一个过程.而不是一个瞬间.图1(a)电键k打到1时,电源给电容充电,当电压与电动势相等时,充电结束.(b)图像就是充电时的电压-时间图像,电键k打到2时,电容放电,电量完全放完放电结束.(c)图像是放电时的电压-时间图像.因为电流i=q/t,q=uc,所以i=uc/t,所以图像的斜率可出电流的特点,可以看出充电时电流是越来越小,放电时电流也是越来越小.
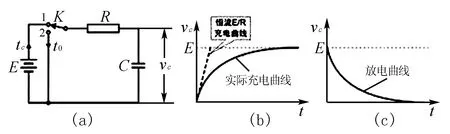
图1
二、电磁感应中的电容
1.恒力作用在切割棒上时电容电路的规律——匀变速直线运动
任何运动受力的分析必须从受力分析开始,电容在电路中会出现充放电,充电与放电就产生电流,由于有了电流就有了安培力,所以必须从安培力的形式下手,由于安培力是个变化的力,所以必须用微元法进行分析,分析安培力的形式,注意这里不能用欧姆定律进行解题.
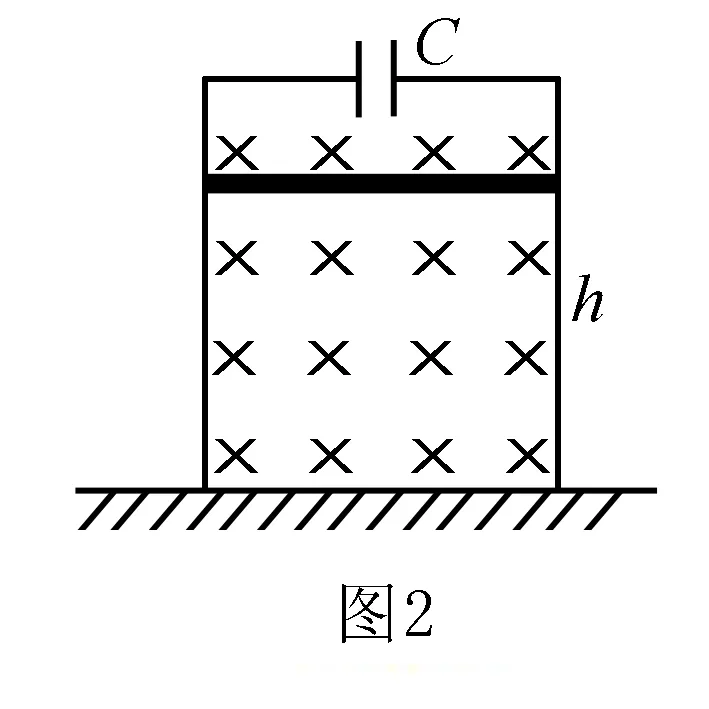
例1 如图2所示,竖直放置在绝缘地面上的金属框架,框架的上端接有一电容为C的电容器,有一质量为m,长为L金属棒与框架接触良好无摩擦平行滑动,h为离地面的高度,匀强磁场强度为B与框架平面保持垂直,开始时电容器没有电量,将棒释放自静止滑下,求棒落到地面的时间t.不计各处电阻.
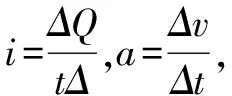
2.无拉力作用时电容电路的规律——先变加速,最后会匀速直线运动
电容电路中导体棒如果不受到拉力,合力就只有安培力的作用了,安培力大小与电流大小有关,电流的大小变化与电容充放电的特点有关,速度的变化引起反电动势的变化,电容两端的电压与感应电动势大小相等从而打到电压的平衡,这样电流的消失,最终会匀速直线运动.
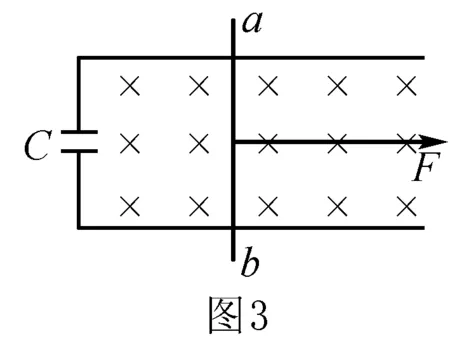
例2 如图3所示,金属杆ab贴着水平平行金属导轨在匀强磁场中沿垂直磁场电容为C的电容器,先用外力拉着金属棒向右方向运动,到有一定速度时突然撤销外力.不计摩擦,则分析棒最终的运动情况可能是( ).
A.简谐运动 B.匀速直线运动 C.匀加速运动 D.匀减速运动
解析这种类型是先有速度,电容上的电量为0.分析必须从受力开始,以金属杆为对象,当外力拉杆ab在匀强磁场中沿垂直磁场方向运动切割磁场时,杆的两端产生感应电动势,电容器此刻被充电,设棒向右为正,使用右手定则判断方向可知:ab中产生的电流从b流到a,所以电容器上正下负.当外力突然消失后,棒将做加速度减小的减速运动,从而电路产生的电动势也相应的减小,所以电路中感应电流会对应的变小,随着时间的推移,当棒产生的感应电动势与电容器两端的电压相等时,电流消失,棒ab受到安培力为0,所以棒最终将做匀速运动,故B正确.故选:B.要强调的是电容的电量不会无限的增大,导体棒也不会无限的减少,只有匀速直线运动才是导体棒最终的状态.
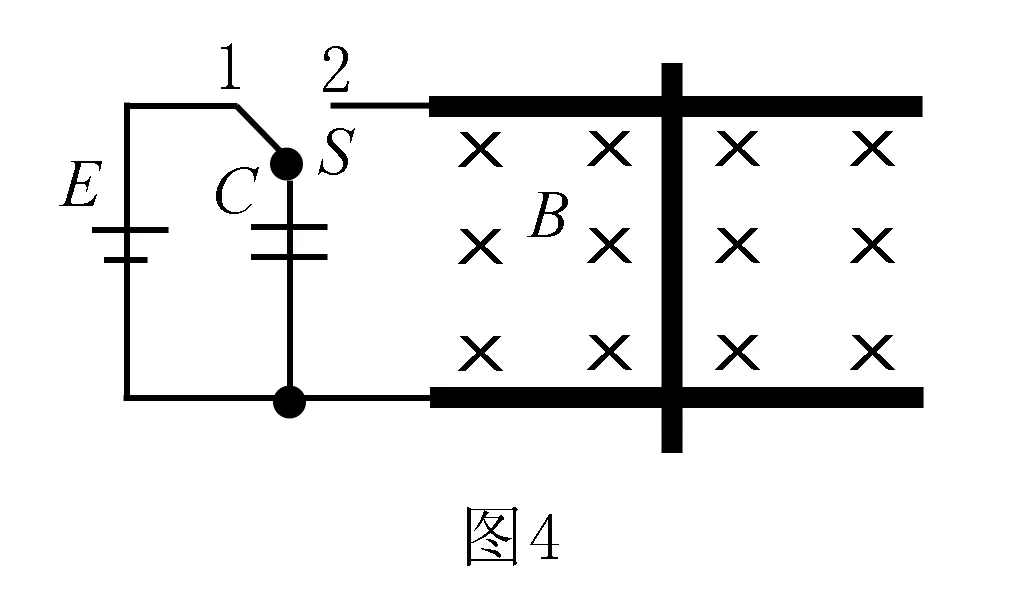
例3 如图4所示,光滑的水平面上有一平行金属导轨,导轨光滑且电阻不计.电源的电动势为E,匀强磁场与导轨垂直.阻值为R的导体棒垂直于导轨静止放置,且与导轨接触.T=0时,将电键S由1掷到2.Q、i、v和a分别表示电容器所带的电荷量、棒中的电流、棒的速度和加速度.图5中正确的是( ).
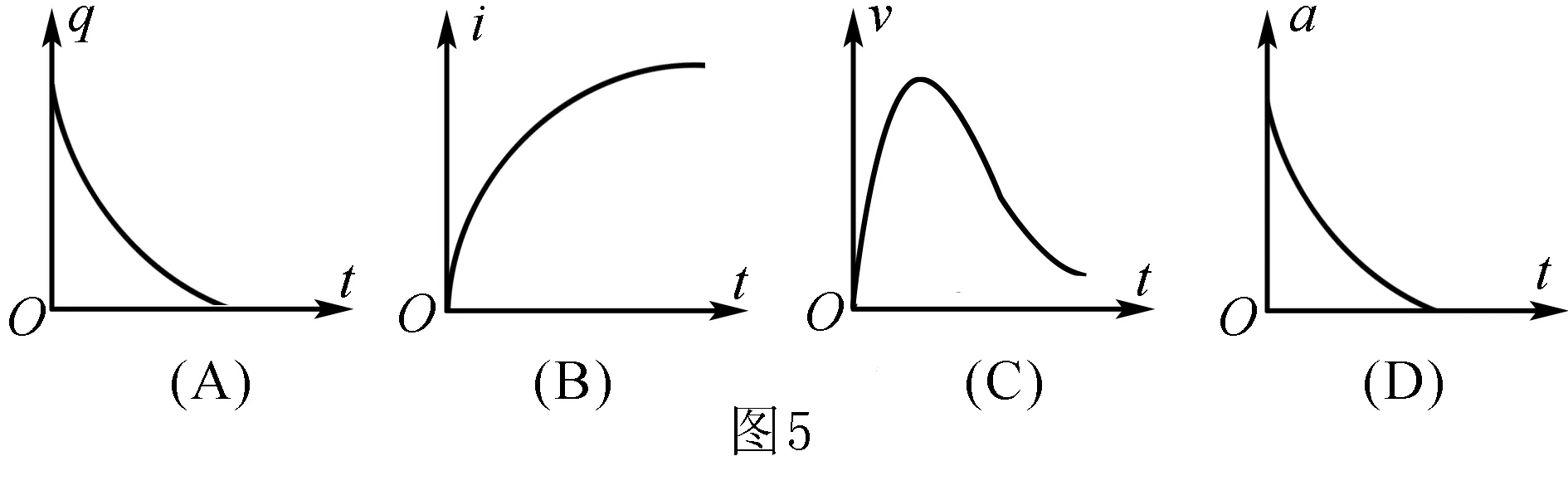
解析这种类型是先有电量,而导体棒的速度为0.开关S打在1时电容被充电,开关打到2时,电容器开始形成放电电流,垂直磁场中的导体棒必然受到安培力的作用,从而产生加速度,速度增大,根据公式感应电动势E=BLv发现速度越大,反电动势也越大,而电容的放电特点可以看出电流变小,从安培力F=BIL得到安培力减小,根据a=F/m很容易得到加速度即减小的结论.所以棒先做加速度减少的变加速运动.这种由于电容器短接放电产生电流使得导体棒在安培力作用下加速运动,而导体棒运动产生反电动势会越来越大.电容上的电压越来越小,感应电动势与电容上的电压两者相等时,电流消失,所以最终导体棒做匀速直线运动.即电容器的电量从此不再变化,所以不会减到0.故选:D.
