解题辩证法

甘志国

(北京丰台二中 100071)

一、有时需要把简单化为复杂来解题

等价转化是解数学题的一种基本思想，通常是把所给的条件逐渐转化，使之越来越简单，该条件就好用了，从而达到解题的目的.

事物都是辩证的.笔者发现，有时在解题的局部过程中，把简单的条件等价转化为复杂的条件来解题反而有助于解题.下面兹举两题.

题1 若“x>1”是“不等式2x>a-x成立”的必要不充分条件，则实数a的取值范围是( ).

A.a>3 B.a<3 C.a>4 D.a<4

解A.由x>1⟺2x+x>3,2x>a-x⟺2x+x>a可得答案.

题2 “a>b”是“3a>2b”的( ).

A.充分不必要条件 B.必要不充分条件

C.充要条件 D.既不充分也不必要条件

二、拼角和拆角

而我们在解某些三角问题时，却需要拼——爱拼才会赢！即不要急着用和(差)角公式sin(α±β),cos(α±β),tan(α±β)展开，而是先把未知的角拼(表示)成已知角的和或差(有时还要把未知角拼成已知角的倍数和)后再解题.下面举题说明这种技巧.

题3 已知=tan(α+β)=3,tan(α-β)=5,求tan2α,tan2β的值.

解可得

tan2α=tan[(α+β)+(α-β)]

tan2β=tan[(α+β)-(α-β)]

证明即证sin(2α+β)-sinβ=2sinαcos(α+β),

sin[(α+β)+α]-sin[(α+β)-α]

=2sinαcos(α+β),

这时再用和(差)角公式展开上式的左边，即知上式成立，所以要证结论成立.

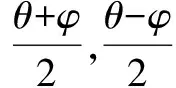
证明先把未知的角β,2α+β拼成已知角α+β,α的差、和，再用和(差)角公式展开，可得要证结论成立.

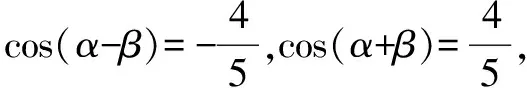
解可求得答案：

cos2β=cos[(α+β)-(α-β)]=…=-1.

题3～8的解法都是拼角.

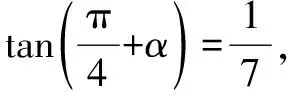
解法1 (拆角)由题设，可得

解法2 (拼角)由题设，可得

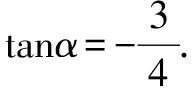
解法1 (拆角)把题设中的等式展开后，可得

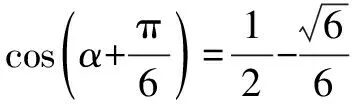
与教科书《必修4》配套使用的《教师教学用书》第130页给出的解答是：

以上解法可能只有极少数同学能掌握，自己能独立想到这种解法的恐怕更少.

下面给出该题的一种直接解法：

若能求出sinx,cosx，则问题即可解决.

唯一解(sinx,cosx).

下面再给出此题的两种巧妙解法：

三、“设而不求”与“设并且求”

在解直线与二次曲线位置关系的平面解析几何题时，经常会用到“设而不求”的方法，往往简便快捷.但笔者发现，有很多时候，把一元二次方程的解求出来(即“设并且求”)也是一种朴素、本质的解题方法——哪怕求出的根的表达式比较复杂.

(1)求椭圆C的焦距；

所以椭圆C的焦距为4.

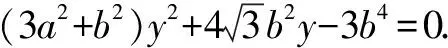
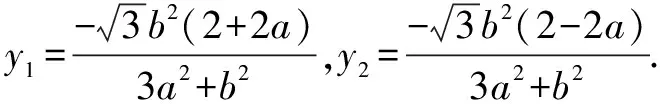
可得(12k2+3)y2+6kcy-k2c2=0.

由-y1=3y2，得

题14 (2006年高考全国卷Ⅱ文科第21题)已知函数f(x)=ax2-2x-2a(a∈R,a≠0)，B={x|10的解集为A，且A∩B≠∅，求实数a的取值范围.

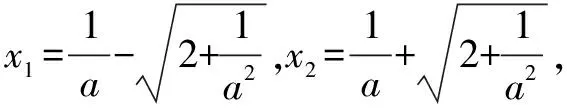
四、不变(静止)与变化(运动)

题15 已知f′(x)=x(x-a)(x-a-1)(a是常数)，求函数f(x)的单调递增区间.

分析要求函数f(x)的单调递增区间，即要求出不等式f′(x)=x(x-a)(x-a-1)≥0的解集.

因为该不等式中有参数a，所以须分类讨论.

在f′(x)的三个零点0,a,a+1中，只有0是不变(静止)的，a和a+1都是变化(运动)的，所以不好分类讨论.但我们可以反其道而行之：如图1所示，在数轴上，先把a和a+1固定下来(注意a+1>a)，再让0在数轴上运动.

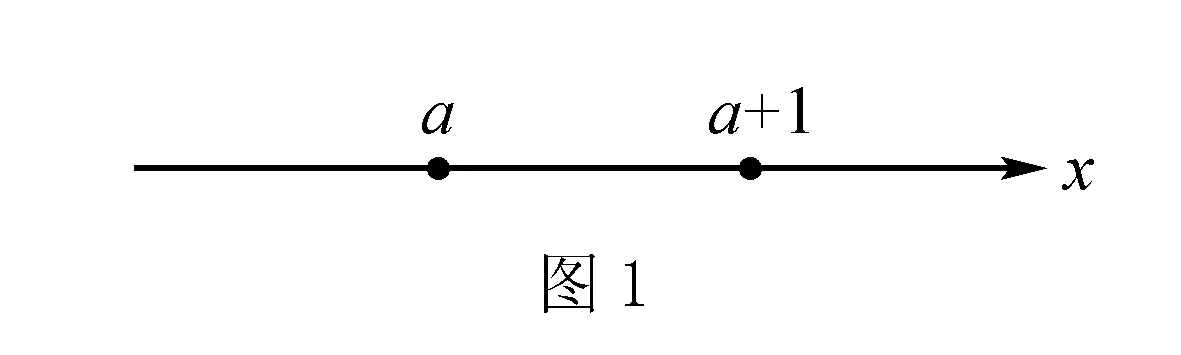
因而可分以下五种情况分类讨论：

(1)当a+1<0即a<-1时，可得f′(x)≥0⟺x∈[a,a+1]∪[0,+∞)，得此时f(x)的单调递增区间是[a,a+1],[0,+∞)；

(2)当a+1=0即a=-1时，可得f′(x)≥0⟺x∈[-1,

+∞)，得此时f(x)的单调递增区间是[-1,+∞)；

(3)当a<0

(4)当a=0时，可得f′(x)≥0⟺x∈[1,+∞)，得此时f(x)的单调递增区间是[1,+∞)；

(5)当a>0时，可得f′(x)≥0⟺x∈[0,a]∪[a+1,+∞)，得此时f(x)的单调递增区间是[0,a],[a+1,+∞).