C波段下窄带多阶切比雪夫滤波器的设计

张凤莉，王 华，代战胜

(商丘职业技术学院, 河南 商丘 476100)

随着电子通信技术的发展，特别是无线通信技术的发展，频谱资源越来越紧张，分配给不同通信系统的频带宽度越来越窄.除了频带资源的紧张之外，对通信设备的低功耗化、小型化的要求也日益提高.在集成设备中，不同的功能模块工作在不同的频带下，由于频带资源的紧张，各个频带之间的缝隙往往比较小，为了防止信号间的干扰，窄带滤波器往往是必不可少的[1].

现在市面上常用的通信设备蓝牙(2.4G)，wifi(2.4G/5G)[1].由于2.4GHz频谱资源特别紧张，5G频带也划给了wifi使用.在5G频带下，通信设备的种类比较少，相互干扰比较少，而5G段的wifi就是工作在C波段的.

现在的手持设备往往是多频带的收发系统，各个收发系统共用一个宽频带天线.在接收信号时，各个系统通过滤波器选择自己的信号，系统内部的各个频带可以通过电子开关来切换.这时就不能再用集总参数来设计电路，要使用传输线的理论来设计电路.即将传统意义的电容电感用微带线来替代，在微波段使用波导、带状线等来传输能量，更容易在PCB板上实现，也更容易和前后级电路连接.

本文使用微带线设计一个带通滤波器，中心频率工作在6GHz，-3dB带宽为300MHz，通带内纹波为0.2dB,过渡带宽为300MHz，阻带衰减为30dB.PCB板的介质厚度为0.6mm，相对介电系数为9.0.为了实现上述设计，本文使用切比雪夫型滤波器来实现.

1 切比雪夫滤波器的设计原理

1.1 切比雪夫表达式

切比雪夫I型滤波器的幅频特性模平方为：

(1)

式(1)中ε是通带内的纹波参数，TN(x)是切比雪夫I型多项式，定义为：

(2)

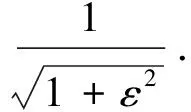
将式(1)的频率用复频率来替换，将系统函数变换到复平面内，则系统函数可以变为：

(3)

为了保证系统的可实现性，所以必须将虚轴左边的极点分给H(s).式(3)中的s/(jω0)为归一化的复频率.式(3)中的极点满足：

(4)

由式(4)计算的极点为：

由式(5)可知所有的极值点是关于虚轴对称的.为了保证系统的因果性，将σk小于0的极值点分给H(s)，剩下的分给H(-s).N等于5时，H(s)极值点sk在复平面上的位置，如图1所示.

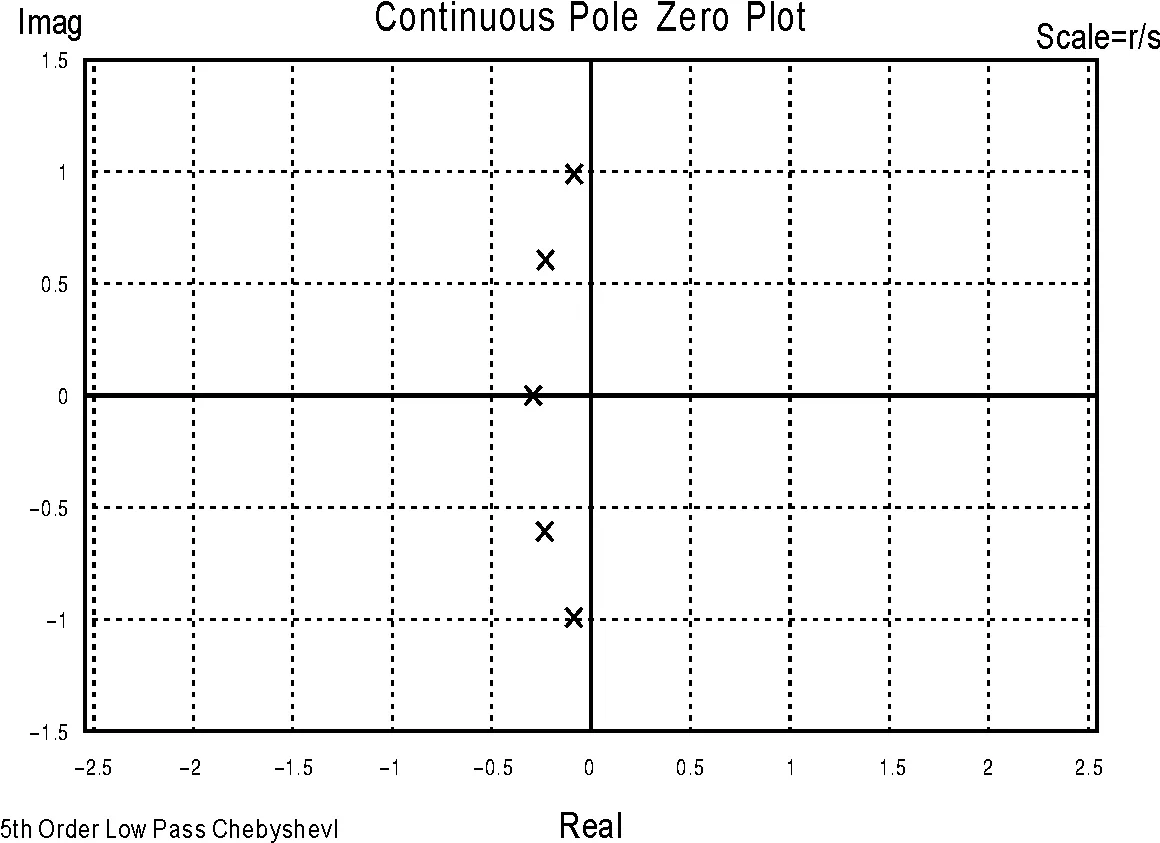
图1 阶数为5的切比雪夫多项式极值点分布

根据上述，可以得出归一化的切比雪夫多项式.式(6)为4阶归一化切比雪夫多项式，式(7)为5阶多项式.

(6)

(7)

根据归一化的多项式，可以得归一化的实现电路[2]，如图2所示.

(a)滤波器电路一 (b)滤波器电路二

1.2 由低通滤波器到带通滤波器的转换

为了求出相对应的带通滤波器，需要将上述的低通滤波器变为带通滤波器.设低通滤波器的频率为ω，高通滤波器的频率为Ω.两者频率满足下述关系：

(8)

低通滤波器的截止频率对应带通滤波器通带的上下频.

(9)

(10)

由上述两式可得，

(11)

式(8)所做的频率变换中，带通滤波器的中心频率是通带上下频的几何平均，而不是算术平均.与一般意义上的带通滤波器稍有不同，上述变换的带通滤波器并不是关于中心频率对称，但是在通频带内部，几乎是关于中心频率对称的.在要求不是特别高的情况下，这种变换是可以满足要求的.低通滤波器的复频率和带通滤波器的复频率有如下关系[2]171-208：

(12)

式(12)中，s′为低通滤波器复频率，s为带通滤波器复频率.

低通滤波器的电感和电容变换到带通滤波器的关系为：

(13)

所以低通滤波器中的电感要变为带通滤波器的电感与电容串联形式，其中电感和电容的变换关系为：

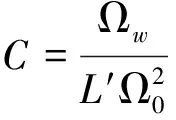
上式中L′是低通滤波器的电感.同理低通滤波器中的电容变为带通滤波器的电感和电容的并联.变换关系为：

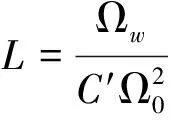
1.3 集总参数电路的实现

前面得到的电感和电容是频率去归一化的结果.微波电路里面一般都是基于50欧姆阻抗的通路.假设微波电路的源阻抗和负载阻抗都是50欧姆.在前面的基础上再进行阻抗的反归一化，可得电感电容为：

将图2(a)中的电路进行反归一化，得到的集总电路，如图3所示.

图3 5阶切比雪夫带通滤波器实现电路

2 C波段滤波器实现结构

当频率达到微波段时，就不能再使用集总参数来设计电路.可以看到图3中，电路中各个元件的值都已经很小了.一小段导线上分布电容电感都可能比上图中电容电感值大，所以在微波段就要使用微带线来设计电路.

微波传输线有很多种，比较常见的有波导(只能传输TM波和TE波)、微带线、带状线和同轴线等.所有这些传输线中只有微带线是最容易在PCB板上实现，而且通过SMA头可以方便的和其他信号相连.这也是微带线最大的优势.下面就通过微带线设计上述滤波器.

2.1 分支线带通实现方案

2.1.1 带通滤波器分支的等效电抗与电纳

从式(8)中可以知道，低通滤波器的频率和带通滤波器的频率并不是线性关系.所以，带通滤波器中的等效电抗和电纳对频率的斜率参量不再是和了.在集总参数中，串联电抗和并联电纳分别是[3]75-145：

(14)

(15)

对应带通滤波器电抗和电纳对频率的斜率参量为[3]75-145：

(16)

(17)

由上述可知，带通滤波器的电感和电纳在线性条件下的等效“电感”和“电容”如式(16)和式(17)所示.

2.1.2 倒置转换器

λ/4传输线的倒置转换关系，如图4所示。

根据微带线的ABCD矩阵，可知图4(a)的电路对应的ABCD矩阵参数为：

(18)

而图4(b)中的ABCD矩阵参数为：

(19)

比较式(18)和式(19)可得图4(a)和4(b)可以相互等效，两式之间的符号只是表示电流或电压的方向不一样[4].

(a)电路原型 (b)等效电路

所以带通滤波器的横向电感与电容串联支路可以等效为LC并联支路，同时两边各有/4的传输线.这样带通滤波器就可以等效为LC并联支路之间再相互并联，两支路之间由/4的传输线相连.

2.1.3 分支线滤波器实现方式

分支线滤波器设计，如图5所示.

图5 分支线滤波器

由于各支路是开路，所以各支路电纳为：

由式(17)可知ζ，所以有：

根据图3中的参数可以计算：

Z01=1052Ω，Z02=5.87Ω，Z03=1701Ω，Z04=5.87Ω，Z05=1052Ω

微带线所能设计的特性阻抗一般在10到200欧姆之间，所以上述的参数使用微带线做不到，故使用分支线实现不了上述滤波器.

2.2 耦合微带线实现方案

平行耦合微带线是利用线端之间的缝隙进行能量耦合，可以得到直接耦合的带通滤波器，如图6所示.

图6 平行耦合带通滤波器

在图6的平行线中，使用奇偶模来分析，可得：

(24)

(25)

J为倒置转换器的系数.根据上面两式可得：

(26)

(27)

根据上述公式和参考文献[3]中的阻抗曲线，可以求得:

W01=W56=0.729mm，W12=W45=0.927mm，W23=W34=0.963mm

s01=s56=0.288mm，s12=s45=1.08mm，s23=s34=1.26mm

L01=L56=4.76mm，L12=L45=4.7mm，L23=L34=4.9mm

设计的耦合微带线滤波器，如图7所示.

图7 平行耦合线带通滤波器

3 结果分析

HFSS中仿真的结果，如图8所示.通过S21参数可以清楚地看到在6GHz处有最大的透射率，也就是在6GHz处负载可以获得最大功率.

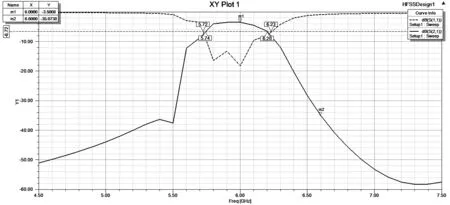
图8 仿真结果图

从仿真结果图上可以看出，在6GHz处也有-3.5dB的插入损耗.这是所有无源滤波器都会有的损耗，在本例中这样的损耗是可以接受的.从图8中可以看到-3dB处的带宽为0.46GHz，频率范围为5.74GHZ至6.2GHz，-3dB的相对带宽小于10%.

4 结 语

本文详细介绍了切比雪夫滤波器的基本原理和集总参数及分布参数中滤波器的设计方法.通过设计过程的分析可以清楚地看到集总参数电路设计与分布参数设计的不同.除此之外，由于电路的工作频率较高，已经达到C波段，通过设计过程可以发现，不管是集总参数电路还是分支型微带线都是难以完成滤波器设计的，只有使用耦合型微带线才能在物理层面具体实现.