判别常数项级数敛散性易犯错误分析研究

景慧丽

(火箭军工程大学 基础部，陕西 西安 710025)

引言

无穷级数是高等数学的一个重要组成部分，它是表示函数、研究函数性质以及进行数值计算的一种工具[1]251.总体来说，无穷级数包括两部分内容：常数项级数和函数项级数，而函数项级数的很多性质和结论都是借助于常数项级数得到的，所以，常数项级数敛散性的判别尤其重要.在高等数学课程中判断常数项级数敛散性的方法有很多，如利用级数收敛与发散的概念、利用收敛级数的性质、利用比值审敛法、利用莱布尼茨定理[1]265等等.每种方法也都有自己的使用条件和使用范围,例如，比值审敛法只适用于正项级数，而莱布尼茨定理只适用于交错级数.但是，笔者在教学中发现，学员在判断常数项级数的敛散性时经常出错，他们不考虑判别法则成立的条件，误用、乱用情况经常发生.为了帮助学员掌握并能熟练应用常数项级数敛散性判别方法，笔者把学员在解题时经常出现的错误进行了分析总结，归纳了常见的错误类型，并且就每种错误给出了例题、错解分析及正确解法.

1 利用级数收敛的必要条件来判断级数收敛

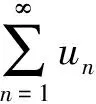
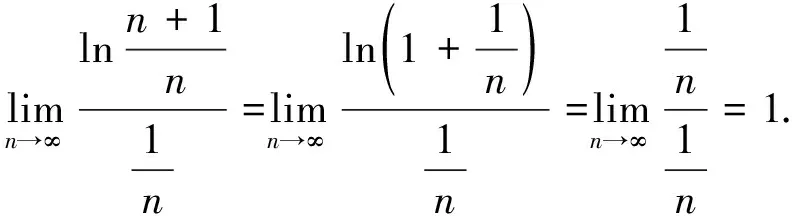
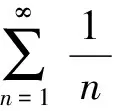
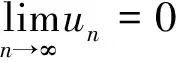
2 颠倒级数收敛与级数的和的逻辑顺序

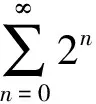
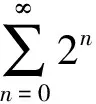
[正确解法] 本题有两种解法.

解法一：利用等比级数的结论，即由于该级数是公比q=2的等比级数，由于|q|=2>1，因此该级数发散.

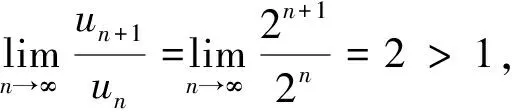
3 用错误的性质来判断级数的敛散性

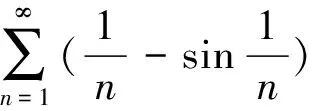
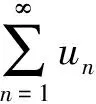
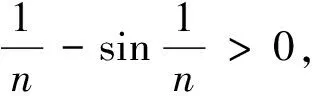
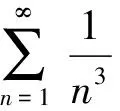
4 乱用比较审敛法(或比较审敛法的极限形式)

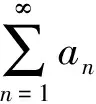
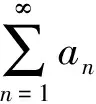
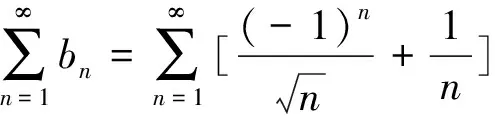
5 误把比值审敛法理解为充要条件

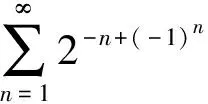
[错解] 令un=2-n+(-1)n，则

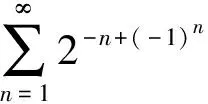
[正确解法] 本题应用正项级数的根值审敛法进行判定

令un=2-n+(-1)n，则

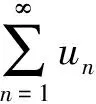
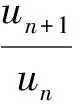
[正确解法] 本题应用正项级数的比较审敛法进行判定.

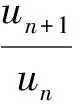
又u3即u3

下面用归纳法证明对任意的n，有un+1成立.

假设un则un+1即un+1成立.

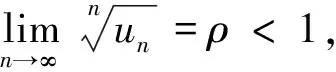
注5 比较审敛法、比较审敛法的极限形式、比值审敛法及根植审敛法都只适应于正项级数，而且这些判别法都是充分不必要的.莱布尼茨定理只适应于交错级数，而且也是充分不必要的，当定理的条件成立时，只能得到级数收敛的结论，当不满足定理的条件时，是不能得到级数发散的结论的.

6 结语

以上就是学员在判别常数项级数敛散性时易犯的错误，其实只要学员理解了级数的概念、性质，掌握了判别级数敛散性方法成立的条件及使用范围，上述错误都是可以避免的.另外，教员要正确看待这些“错题”资源，这些都是非常宝贵的教学资源，正如心理学家盖耶所说：“谁不考虑尝试错误，不允许学生犯错误，就将错过最富成效的学习时刻.”[3]在教学中，教员要主动挖掘学员“错题”中的“闪光点”，及时进行探究、分析和讲评，既可以为学员创造新的学习机会，提高教学质量，还可以培养学员的问题意识，培养学员发现问题、解决问题的能力[4].