井底岩石的共振响应分析及数值模拟研究
2019-03-23宋恒宇李根生史怀忠黄中伟宋先知杨睿月
宋恒宇, 李根生, 史怀忠, 黄中伟, 宋先知, 杨睿月
(中国石油大学(北京) 油气资源与探测国家重点实验室,北京 102249)
钻井提速和高效破岩是油气井领域的重要研究内容。在石油天然气勘探开发逐渐向深部地层发展,所钻地层越来越坚硬、越来越复杂的大背景下,研究高效破岩技术与方法十分必要。针对于此,国内外专家、学者提出了许多钻井提速新概念和新技术,共振钻井就是其中一个较为可行的提速技术。其实现方法如下:利用共振钻井设备对地层岩石持续施加呈周期性变化的冲击力,使冲击力的振动频率接近岩石的共振频率,岩石随之发生共振,其振幅会达到最大,从而改变岩石内部的位移分布,加速岩石的破坏。目前,共振钻井技术已经运用到了相关领域,一部分专家学者也对其破岩机理、破岩效果进行了研究,得到了冲击力激励下岩石介质的响应机制和岩石介质的共振特性。李思琪[1]研究了岩石介质冲击振动的力学模型,并基于接触力学理论,分别建立了动静载荷作用下锥形压头和球形压头在加载阶段和卸载阶段的破岩模型。李玮等[2]研究了基于重整化方法的冲击载荷下岩石振动分析,得到当钻头高频振动频率和岩石固有频率接近时,岩石振动幅度和振动速度最大,即达到了共振。李玮等[3]进行了高频振动钻具冲击下岩石响应机理及破岩试验分析,得到高频振动冲击能够降低岩石的抗钻能力,提高破岩效率。田家林等[4-5]研究了高频微幅冲击振动作用下岩石破碎行为计算方法,得到高冲击频率、低幅值能够增加破岩体积、减小破岩比功、增加岩石裂纹长度等结论。董学成等[6-7]进行了振荡冲击器破岩机理的数值模拟分析,得到了井底岩石的破碎效率与振荡冲击器工作频率的关系。Wiercigroch等[8]提出了共振提速钻井(RED)技术,并设计生产了相应的设备,通过钻头的轴向振动激发地层岩石,使其达到共振状态,该技术对硬岩的提速效果十分明显。
综上所述,在理论研究方面,大多数学者都是通过建立简单的振动模型[9], 研究岩石介质在自由状态下的振动规律,没有考虑到井底岩石不仅属于多孔介质,而且还受到围压作用[10-13]。本文在前人基础上,考虑到岩石内部孔隙,以及其受到的井底围压作用,研究其共振响应特性,得到不同约束下、不同孔隙分布下,岩石的位移响应振幅与冲击力频率的关系,分析结果可以为共振钻井技术提供一定的理论指导。本文模拟的冲击力为钻头整体对地层岩石施加的冲击力。
1 岩石振动方程的建立及响应分析
根据相关文献,选择开尔文体作为岩石的振动模型,该模型是一种典型的、具有一定代表性的岩石力学组合模型,也是岩石动力学的基本模型[14]。开尔文体的组合模型如图1所示。
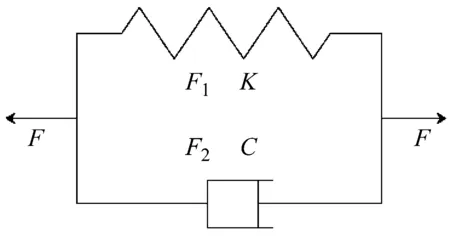
图1 开尔文体组合模型
加载的谐振激励符合正弦变化规律,振动方程如下
(1)
式中:m物质系统的质量(kg);C为阻尼系数(Ns/m);X为振动位移(m);t为时间(s);k为刚度(N/m);F为谐振冲击力(N);ω为谐振冲击力频率(Hz);A为谐振冲击力振幅(m)。
(2)
式中:a即为位移响应振幅。
(3)
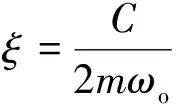
(4)
式中:ωo为岩石的固有频率
根据冲击与振动理论,可得位移共振频率与固有频率之间的关系
(5)
式中:ξ为相对阻尼系数;ωr为位移共振频率(Hz)。
计算参数取值,如表1所示。

ωo分别取值900、1 000、1 500、2 000,绘制响应振幅与冲击力频率之间的关系曲线。
由图2可知,当冲击力频率接近共振频率时,位移响应振幅最大,即达到了共振。并且共振频率越小,对应的最大响应振幅越大。
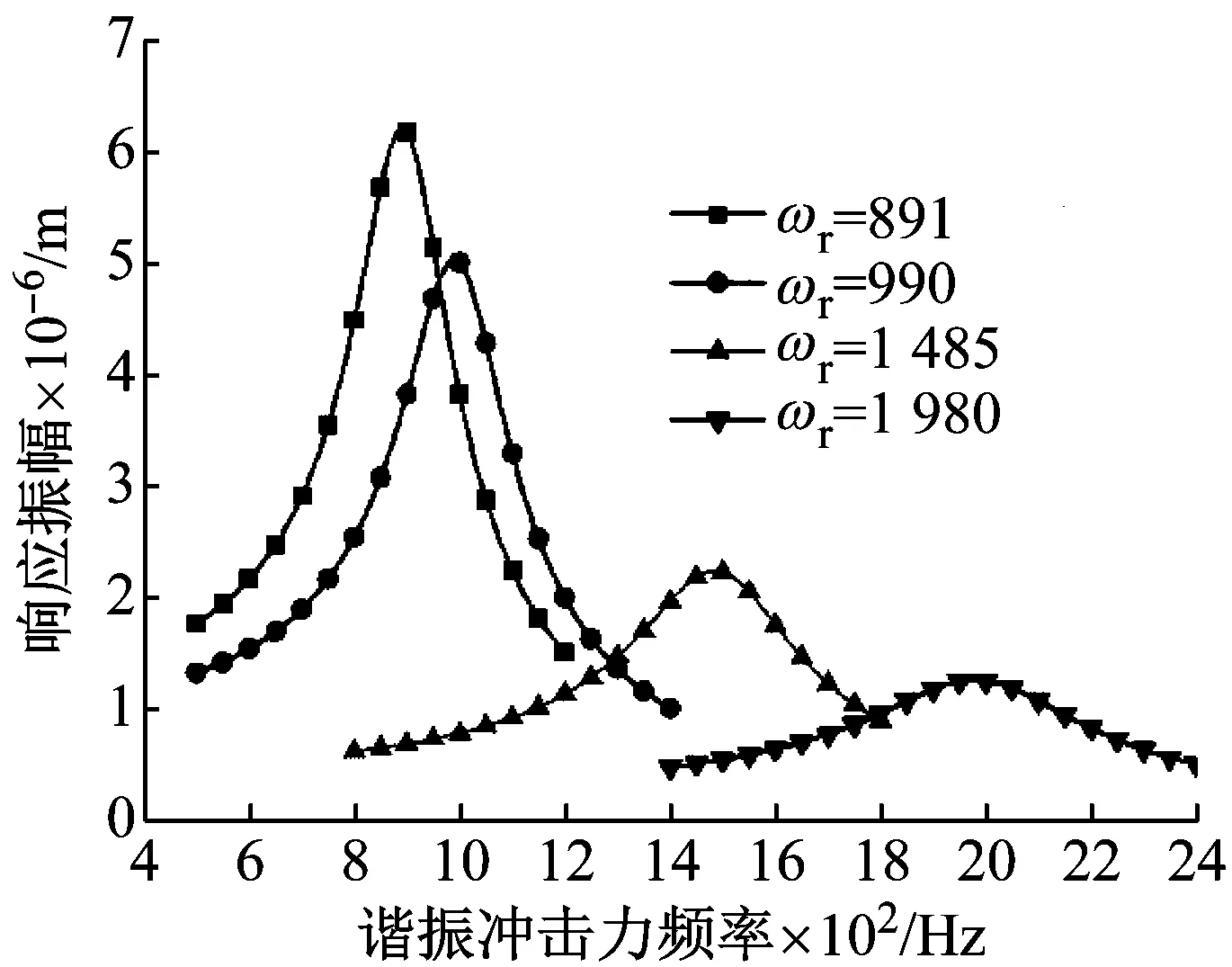
图2 模型位移响应振幅与谐振冲击力频率之间的关系
Fig.2 The relationship between the displacement responding amplitude and the impact force frequency
2 岩石所受约束条件对其共振频率的影响
由以上分析可知,物质系统的共振频率与固有频率密切相关。所以当物体的刚度和质量发生变化时,共振频率会随之发生变化。现推导出刚度与弹性模量的关系,首先建立如图3所示圆柱形岩石物理模型。

图3 岩石物理模型
(6)
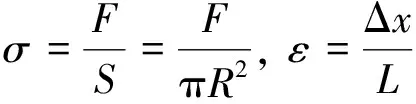
(7)
联立式(6)和(7),得:
(8)
式中:F为轴向力(N);R为模型底面半径(m);L为模型高(m); Δx为轴向形变量(m);E为弹性模量(Pa);σ为轴向应力(Pa);ε为轴向应变(1);S为模型底面面积(m2)。
当模型侧面受到约束时,其轴向刚度可能会发生变化,而刚度的变化会直接影响岩石的固有频率以及施加冲击力时的共振频率。现考虑两种情况,一是侧面受到大小固定的围压,二是侧面受到径向的位移约束,分别分析该岩石模型在这两种情况下轴向刚度的变化以及共振频率的变化。
首先分析其受到围压作用,X,Z方向分别为σx,σz,轴向受到应力σy,根据广义胡克定律和刚度定义,满足如下方程
(9)
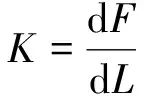
(10)
式中:μ为泊松比
式(9)两边同时分别对εy和σy微分,因为σx,σz保持不变,同时联立式(10),可以得到刚度的计算公式
(11)
由式(11)可知当模型侧面受到固定围压时,其轴向刚度不变,因此其轴向共振频率亦不变,所以岩石模型的共振频率与所受围压的大小无关。
根据前文所述,共振钻井的提速机理就是岩石在钻头冲击作用下达到共振状态时更容易发生破碎。为了把钻头的冲击能量集中在井底岩石的中心区域,降低其向井筒外区域的耗散,同时也为了更容易地实现井底岩石的共振效果,通常选择双级钻头[15]。双级钻头包括下部小尺寸的冲击破岩钻头和上部大尺寸(与井眼尺寸相匹配)的扩眼钻头。共振钻井中,为了使冲击能量更好地破碎井眼内的岩石,下部钻头的尺寸选择应该有两个限定条件:① 下部钻头尺寸不宜过小,否则其冲击能量不能波及整个井眼内岩石,不能高效地对井眼内岩石造成损伤和共振破碎;② 下部钻头尺寸不宜过大,否则其冲击能量会向井眼外区域扩散,造成冲击能量的浪费,同时也会对井壁稳定造成干扰。
根据上述约束条件,可以选择合适的钻头尺寸。在满足上述条件的下部钻头冲击作用下,可以认为井壁处于冲击远端区,此时可以忽略掉井筒以外岩石的变形(波及到井筒外区域的冲击能量很少),此时岩石模型的径向变形就可以忽略。当模型侧面受到径向的位移约束时,即其侧面沿径向上的位移和应变为0,同样可以根据弹塑性力学的理论,建立如下方程
(12)

(13)
岩石模型的侧面径向应变为0,即满足
εx=εz=0
(14)
联立式(12)~式(14),可得
(15)
代入如下轴向应力、应变方程
(16)
可以得到

(17)
化简得
(18)
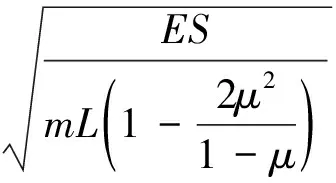
(19)

(20)
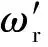
由式(20)可知,当岩石模型受到径向位移约束时,其相对共振频率与岩石模型的泊松比相关,绘制相对共振频率与泊松比的关系曲线,如图4所示。
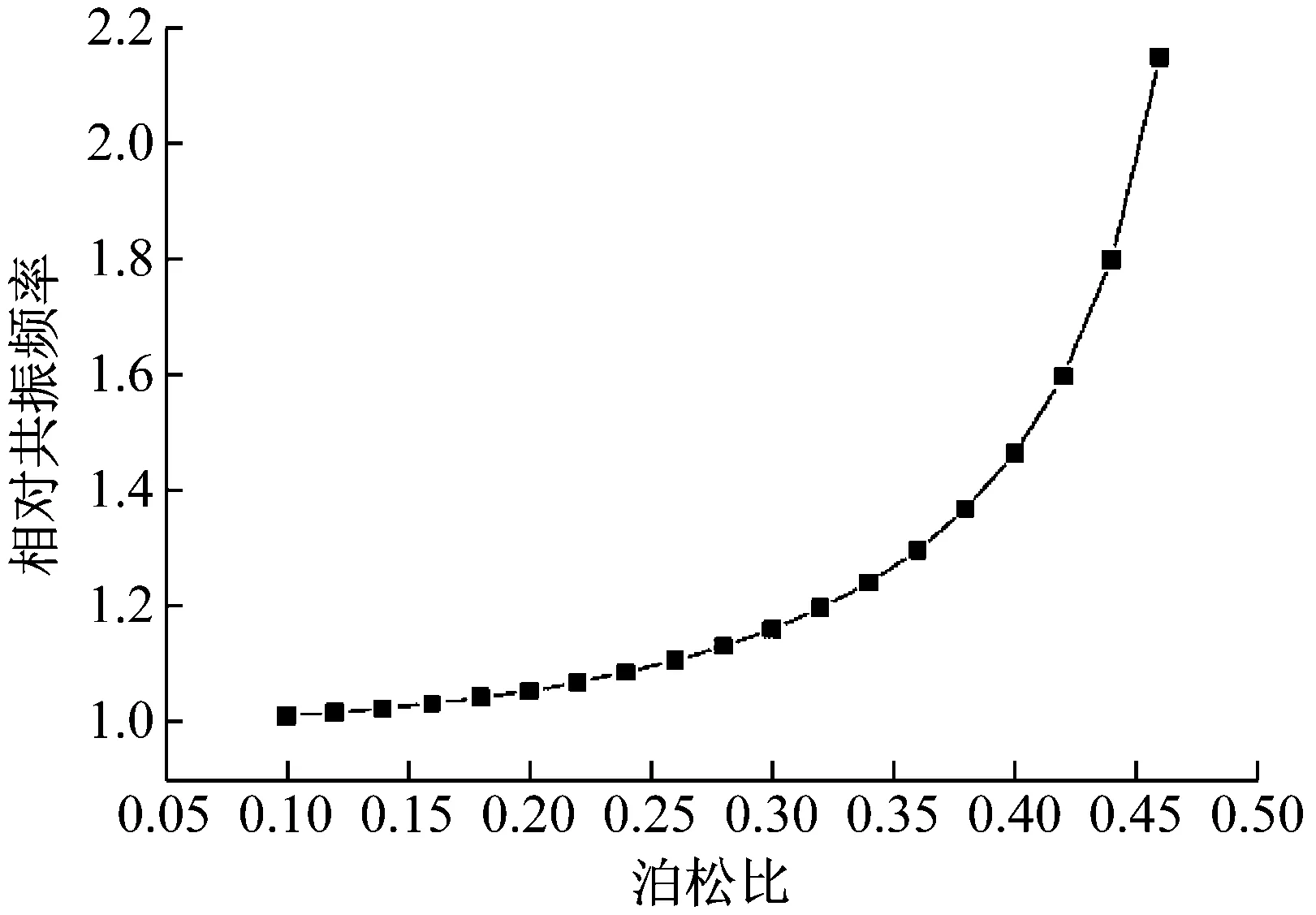
图4 相对共振频率与泊松比的关系曲线
由曲线可以明显看出,当模型侧面受到径向固定约束时,其相对共振频率随之增大。相对共振频率与泊松比有关,泊松比越大,相对共振频率越大,且其变化率亦随之增大。
3 岩石内部孔隙对共振频率的影响
井底岩石属于多孔介质,岩石内部的孔隙可能会对共振频率造成影响,现分三种情况。
3.1 模型孔隙分布均匀
因为岩石模型的孔隙结构分布均匀,所以垂直于轴向的任一截面上孔隙所占截面的面积比均等于孔隙度,此时岩石截面的有效承压面积为S(1-φ),联立式(3)、(5)、(8),可得共振频率的计算公式

(21)
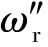
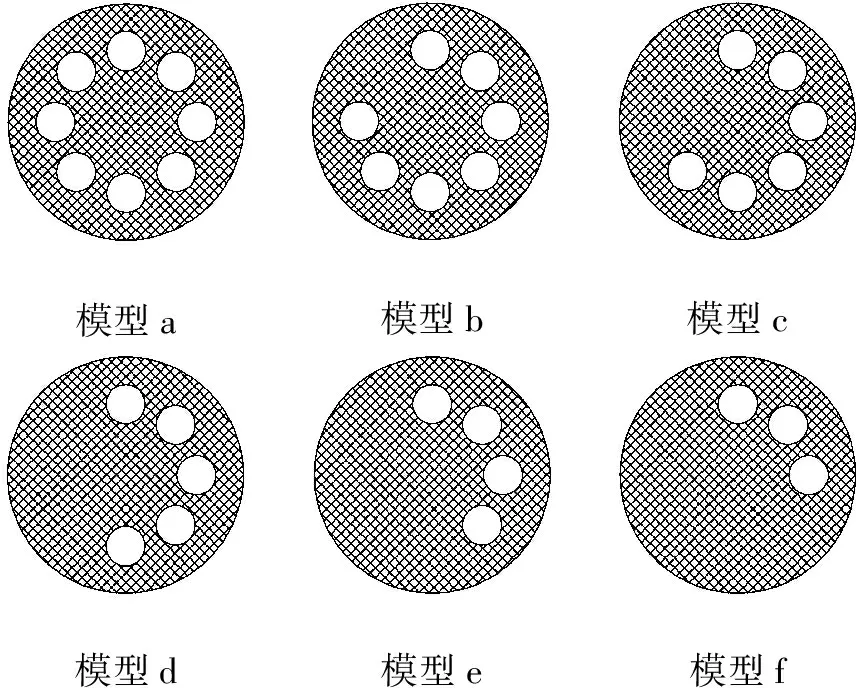
由式(21)可知,当岩石内部存在沿轴向分布均匀的孔隙时,岩石模型的共振频率与孔隙度无关,只与岩石模型的刚度、密度、长度、阻尼大小相关。
3.2 模型孔隙沿径向分布不均匀
考虑到此时研究的孔隙结构,不需要考虑其连通性和渗透性,只需要考虑其分布特征,因此采用球管孔隙模型[16]来模拟岩石模型的孔隙结构,为了方便理论推导,只建立圆管部分。而且保证孔隙结构沿轴向(即沿激励冲击方向)分布均匀。建立的模型外观同图3,横截面如图5所示。
用以上六种模型来模拟孔隙沿径向分布的不均匀性。因为以上模型孔隙度沿轴向分布均匀,所以理论计算公式与式(21)相同,结果亦相同。
3.3 模型孔隙沿激励冲击方向分布不均匀
假定孔隙沿轴向呈线性变化,同样用圆管部分来模拟孔隙结构,并建立锥形圆管模型来表征孔隙沿轴向分布的不均匀性,如图6所示。

图6 孔隙沿轴向分布不均匀的物理模型
原模型的共振频率为

(22)
根据式(8),计算如上物理模型的共振频率,首先把模型沿轴向分成n份,所以第i部分的刚度为
(23)
模型的整体刚度为
(24)
把极限式转化为积分式,得到
(25)
模型的质量为
(26)
模型的共振频率为
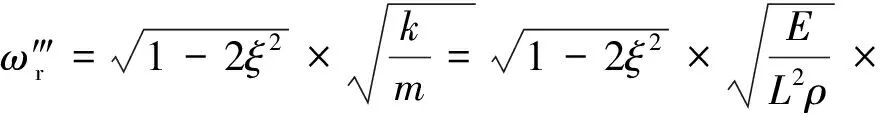
(27)
模型的相对共振频率为
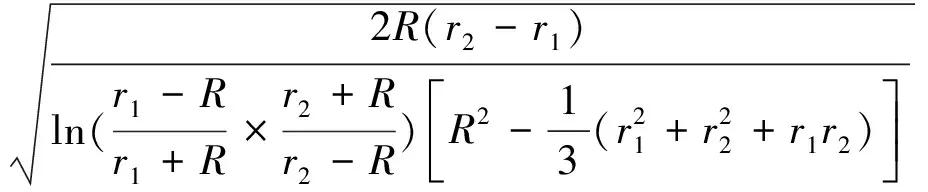
(28)
式中:ω‴r为孔隙结构沿轴向分布不均匀时,岩石模型具有的共振频率;ω‴r/ωr为相对共振频率。
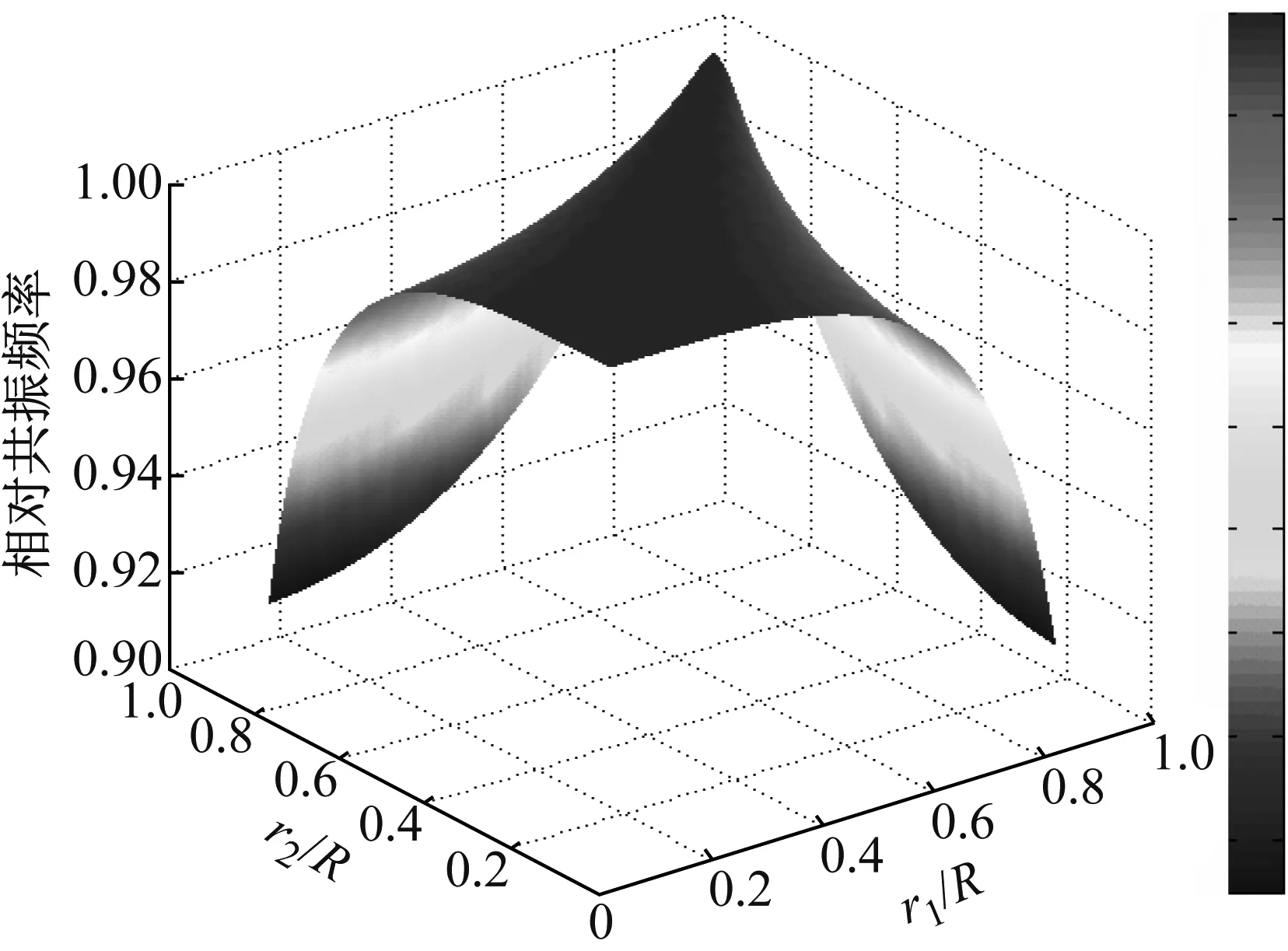
(a)

(b)
根据式(28),并为r1/R、r2/R赋予不同的参数值,绘制如图7所示的相对共振频率与r1/R、r2/R之间的关系曲线。从图中可以看出,r1,r2的差值越大,相对共振频率越低,图7(b)的对角线表示r1=r2,此时相对共振频率等于1,与3.1中均质的结果一致。
4 数值模拟
为岩石模型赋予如下参数值,分析其共振响应。物理参数、几何参数取值如表2。
利用有限元软件,Abaqus的动力学分析模块,对以上所建立的模型进行模拟计算,载荷加载方式如图3所示,右侧底面加载正弦型周期性变化的冲击力载荷,根据模型的截面具体情况选择集中力或者均布面力,当岩石模型内部无孔隙结构时,在右侧底面中心加载集中力;当岩石模型内部有孔隙结构时,在右侧底面上加载均布面力。模型左侧底面统一固定。模型侧面根据具体情况,选择无约束自由状态、加载围压或者施加径向约束。划分网格时,统一选择四面体网格。通过模拟,在不同条件下,得到如下响应振幅与冲击力频率之间的关系。
4.1 不同冲击力下的位移响应
冲击力振幅取值分别为10 kN、30 kN、50 kN和80 kN。图8绘制的是岩石模型在不同冲击力振幅下位移响应与冲击力频率之间的关系曲线, 岩石模型的最大响应振幅均在1 950 Hz处发生,该频率即是岩石模型的共振频率。当冲击力频率小于共振频率时,岩石模型的位移响应振幅随着冲击力频率的升高而升高;当冲击力频率大于共振频率时,岩石模型的位移响应振幅随着冲击力频率的升高而降低,且位移响应振幅变化图像基本关于共振频率对称。在四种冲击力振幅下,振幅越大,共振位移响应振幅就越大。
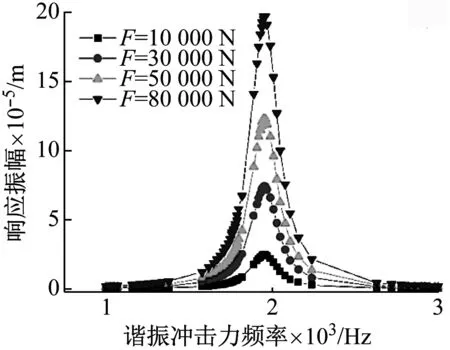
图8 岩石模型在不同冲击力振幅下位移响应与冲击力频率之间的关系
4.2 不同围压约束下的位移响应
4.2.1 不同约束下
该过程模拟了三种围压以及侧面径向约束下的共振响应,围压值分别为10 MPa、20 MPa和40 MPa,冲击力振幅取值80 kN。图9绘制的是岩石模型在不同约束下位移响应与冲击力频率之间的关系曲线。从三条围压下的位移响应曲线可以看出,当岩石模型受到固定围压时,其共振频率不随围压的变化而变化,基本维持在2 050 Hz,且响应曲线不关于共振频率对称,当冲击力频率小于共振频率时,随着冲击力频率的增加,位移响应振幅升高很快,而当冲击力频率大于共振频率时,随着冲击力频率的增加,位移响应振幅下降的速度变缓,而且随着围压的增大,响应振幅亦随之增大。当岩石侧面受到径向位移约束时,其共振频率略高于围压下的共振频率,达到了2 120 Hz,且其共振响应振幅略低,响应曲线大致关于共振频率对称。总之,当岩石模型侧面受到约束时,其共振频率高于自由状态下岩石模型的共振频率。受到侧面径向约束时,岩石模型的共振频率升高这一现象在理论计算上已经得到了解释;而当岩石模型受到侧面围压时,如果按照理论推导的结果,其共振频率应该与自由状态下的共振频率相等,但实际模拟显示的结果是略高,出现这种现象的原因可能是加载的围压对一直处于动态变形岩石的作用有一定的滞后性,类似于产生了一定的径向约束,因此共振频率有所升高。此过程中的模拟结果与理论分析的结果基本相一致。
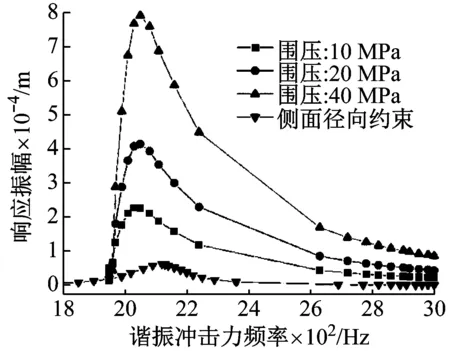
图9 岩石模型在不同约束下位移响应与冲击力频率之间的关系
4.2.2 受到径向位移约束时
该过程模拟了受到径向位移约束的岩石模型在不同泊松比取值情况下的共振响应,泊松比取值分别为0.2、0.3、0.35和0.4,冲击力振幅取值80 kN。图10绘制的是岩石模型在不同泊松比下位移响应与冲击力频率之间的关系曲线。从图10可以看出,当岩石模型受到径向位移约束时,其共振频率与岩石自身的泊松比有关,且泊松比越大,岩石模型的共振频率越大。从图10还可以看出,在加载冲击力振幅相同的情况下,最大响应振幅随着岩石模型泊松比的增加而降低。从图11可以看出,随着泊松比的增大,岩石模型的共振频率不仅随之增大,而且其增加速度也越来越快。该模拟结果基本与理论分析结果相一致。

图10 岩石模型在不同泊松比下位移响应与冲击力频率之间的关系
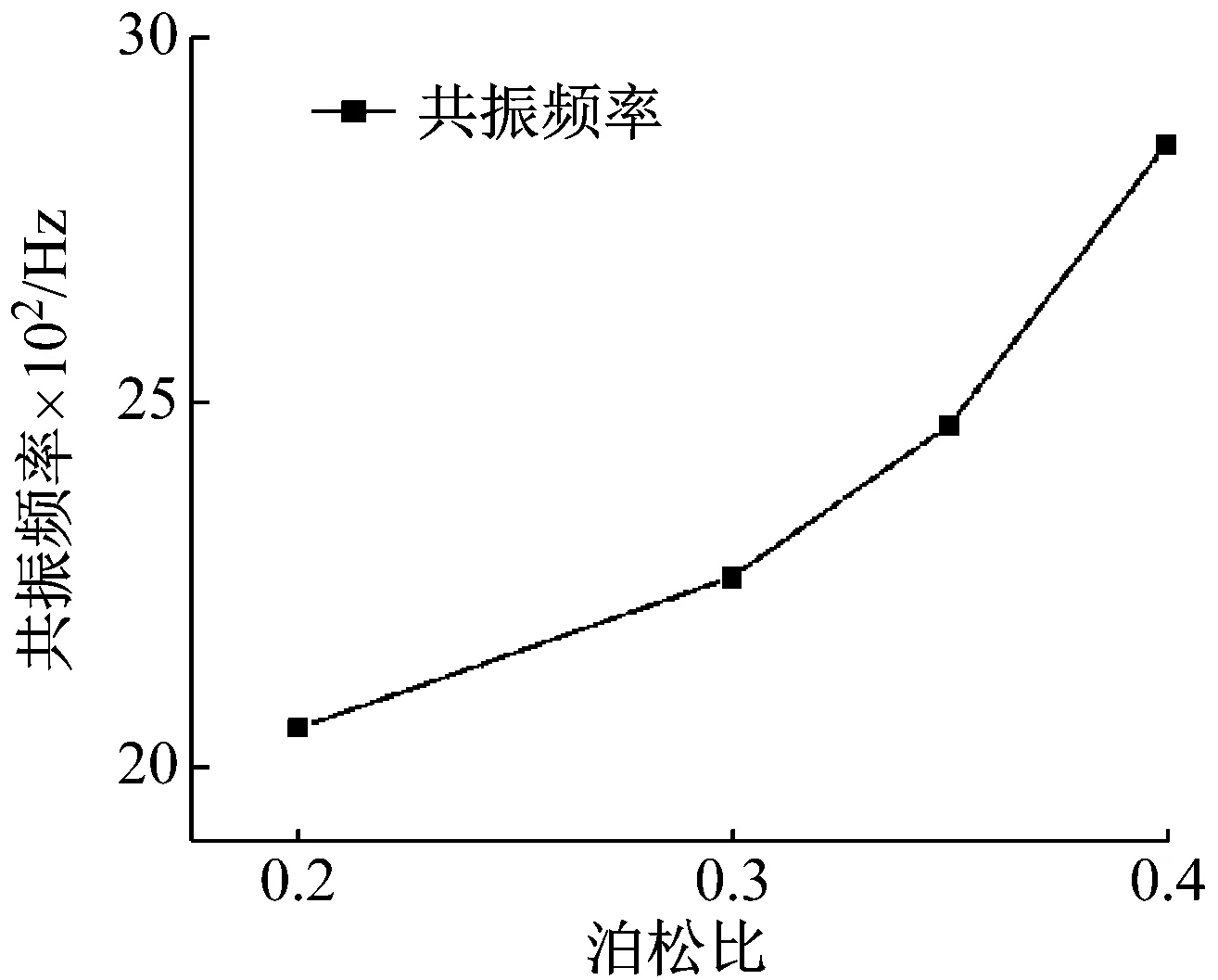
图11 岩石模型的共振频率随泊松比的变化关系
4.3 不同孔隙结构分布下的位移响应
4.3.1 岩石模型的孔隙结构分布均匀
构建内部含有孔隙结构的岩石模型,孔隙度分别为0.857%、3.43%、30.86%。图12绘制的是岩石模型在不同孔隙度下位移响应与冲击力频率之间的关系曲线。三种孔隙度下的位移响应曲线基本重合,因此,在该数值模拟条件下,当岩石模型内部孔隙沿冲击力方向分布均匀时,其共振频率不随孔隙度大小的变化而变化,共振频率亦为1 950 Hz,且具有孔隙结构的岩石模型的响应曲线与不具有孔隙结构的响应曲线相似。该模拟结果与理论分析结果相一致。

图12 岩石模型在不同孔隙度下位移响应与冲击力
4.3.2 岩石模型孔隙沿径向分布不均匀
建立图5中的六种模型,来模拟孔隙沿径向分布的不均匀性。
如图13所示,孔隙沿径向分布的不均匀程度对岩石模型的响应振幅无影响,各模型的响应曲线大致重合。

图13 不同模型下位移响应与冲击力频率之间的关系
4.3.3 岩石模型孔隙沿激励冲击方向分布不均匀
按照图5的模型结构,分别给r1,r2赋值,得到不同的孔隙不均匀程度,并用γ来表征
γ=r2-r1/L
(29)
岩石模型的参数赋值如表3。
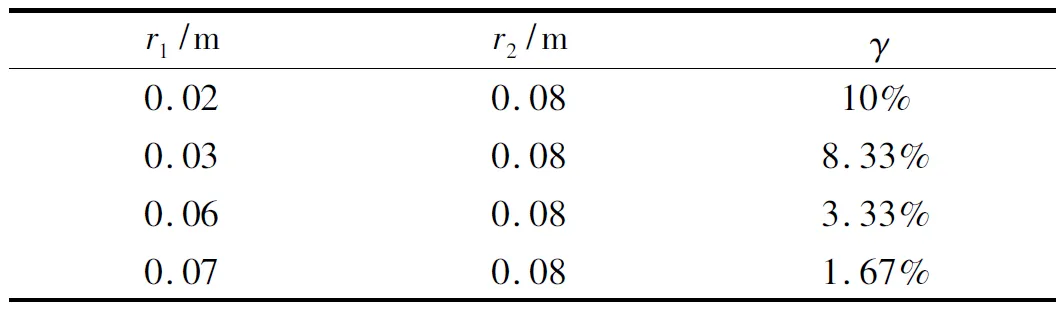
图14绘制的是岩石模型在不同孔隙分布不均匀程度下位移响应与冲击力频率之间的关系曲线,图15绘制的是共振频率与不均匀程度的关系曲线。从图中可以看出,岩石模型的孔隙分布不均匀程度越大,岩石模型的共振频率越低,而且在加载同等大小的冲击力振幅条件下,不均匀程度越大,岩石模型位移响应的最大振幅越大。在该条件下的响应曲线基本关于共振频率对称。从图15可以看出,随着孔隙分布不均匀程度的增大,岩石模型的共振频率随之下降,但其下降速度越来越慢。该模拟结果与理论推导结果相一致。

图14 岩石模型在不同孔隙分布不均匀程度下位移响应与冲击力频率之间的关系
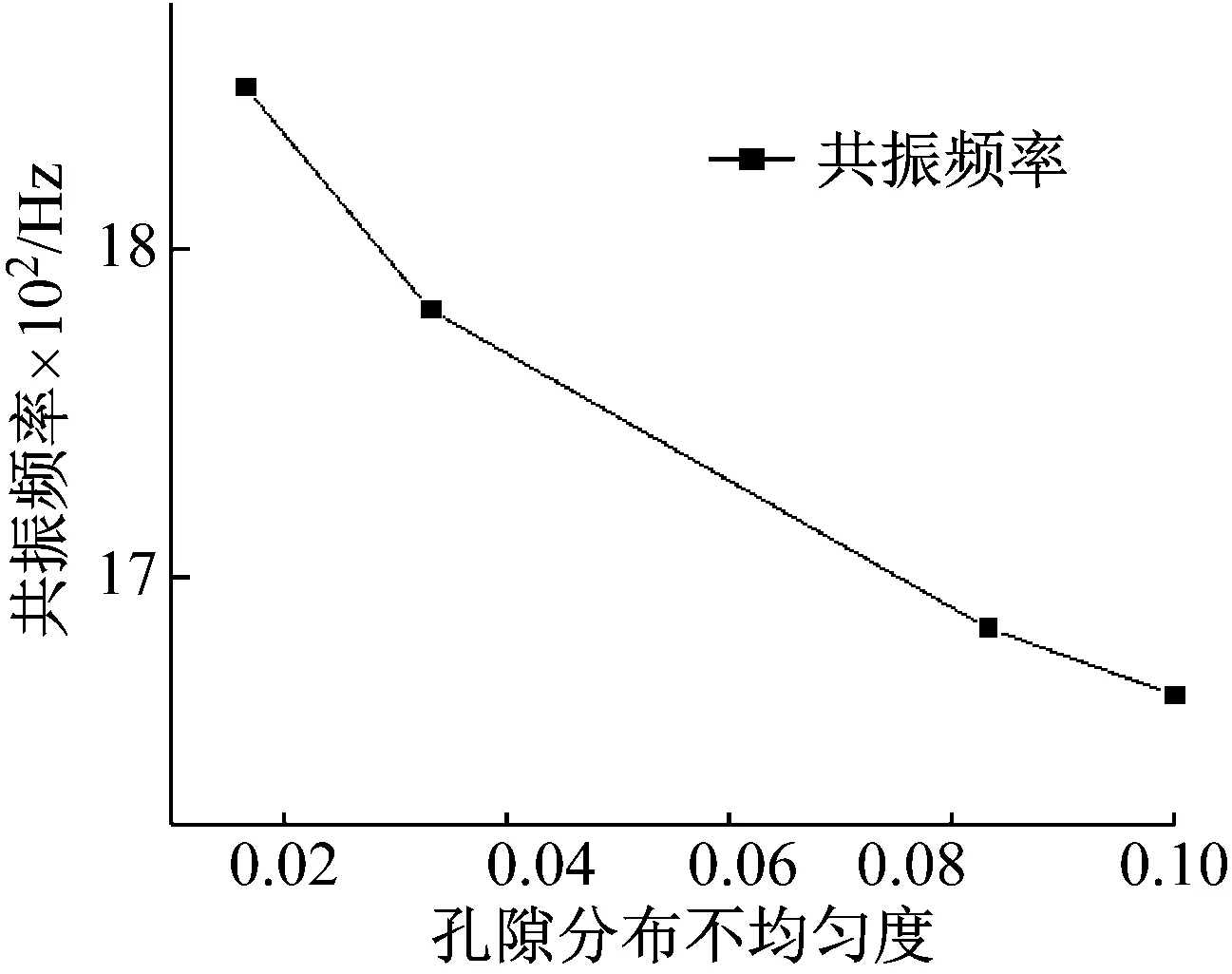
图15 岩石模型的共振频率随孔隙分布的不均匀程度之间的关系
下一步还需要开展室内试验,来验证岩石在实际状态下的共振响应规律及其共振频率的变化规律,为共振钻井技术提供更多理论支持,促进共振提速钻井技术的发展。
5 结 论
(1) 在该模拟条件下,当岩石受到固定围压时,其共振频率不随围压大小的变化而变化,且响应曲线不关于共振频率对称,当冲击频率小于共振频率时,随着冲击频率的增加,位移响应振幅升高很快,而当冲击力频率大于共振频率时,随着冲击力频率的增加,位移响应振幅下降的速度变缓。当岩石侧面受到径向位移约束时,其共振频率略高于围压下的共振频率,但其响应振幅略低于围压下的响应振幅。
(2) 当岩石受到径向位移约束时,其共振频率与岩石自身的泊松比有关,且泊松比越大,共振频率越高,同时共振频率的增加速度也随之增大。在冲击力振幅相同的情况下,最大响应振幅随泊松比的增加而降低。
(3) 当岩石内部孔隙沿冲击力方向分布均匀时,其共振频率不随孔隙度大小的变化而变化,且具有孔隙结构的岩石的响应曲线与不具有孔隙结构的响应曲线类似。
(4) 当岩石内部孔隙沿冲击力方向分布不均匀时,不均匀程度越大,岩石模型的共振频率越低,同时共振频率的下降速度随之变慢。而且在加载同等大小的冲击力条件下,不均匀程度越大,岩石响应的最大振幅越大。
