考虑弹流润滑影响的表面局部缺陷中介轴承动力学建模
2019-03-23艾延廷张凤玲
田 晶, 艾延廷, 赵 明, 孙 丹, 张凤玲
(1. 西北工业大学 动力与能源学院,西安 710072; 2. 沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136)
现代双(多)转子航空发动机支承方案多采用中介轴承结构。中介轴承位于高、低压转子之间,相对转速高,动载荷较大,润滑困难,且工作温度高,极易发生故障[1-2]。中介轴承故障会造成发动机振动超标,甚至发生空中停车等灾难性事故。建立有效的带局部缺陷的中介轴承动力学模型,可以准确的分析故障轴承的动力学行为,获取中介轴承早期故障特征。因此,开展中介轴承故障动力学建模研究对航空发动机故障诊断技术发展具有重要的理论意义和工程价值。
目前,滚动轴承局部缺陷动力学建模方法受到国内外学者的广泛关注,并取得了一些研究成果。Sunnersjo[3]最早将滚动体等效为非线性弹簧,并建立了两自由度模型,但该模型仅能就某一瞬时状态进行动力学分析。同时期的Gupta[4-5]也建立了多种轴承动力学模型,但模型均未考虑滑油的影响。McFadden等[6]建立了轴承内环存在单点和多点故障的动力学模型,获取了两种故障的振动特征。Tandon等[7]提出了一个解析模型,预测了轴承内、外圈及滚动体上存在缺陷时的振动状态。Kulkarni等[8]采用三次Hermite样条函数模拟轴承故障产生的脉冲,研究了载荷大小和外环缺陷尺寸、位置对轴承振动响应的影响。刘静等[9]考虑了时变位移激励与故障尺寸的关系,并基于Hertz接触理论建立了球轴承的故障动力学模型。徐可君等[10]提出了一种带滚动体缺陷的中介轴承动力学模型,但没有考虑动压润滑对模型的影响。针对滚动轴承局部缺陷的动力学建模研究较多,但对中介轴承缺陷动力学建模研究较少,且模型多未考虑润滑油膜的影响。
本文以中介轴承为研究对象,在非线性Hertz接触理论的基础上,提出并建立了一种考虑时变位移激励和弹流润滑影响的中介轴承局部缺陷动力学模型,并进行了故障模拟实验。对比分析了动力学模型模拟结果和故障实验结果,验证了所建立模型的准确性。
1 动力学模型建立
1.1 中介轴承简化及假设
中介轴承位于航空发动机高低压转子之间,轴承的内、外圈随着高、低压转子同时旋转。内、外圈既可以同向旋转又可以反向旋转,中介轴承支承形式如图1所示。

图1 中介轴承支承形式
航空发动机中介轴承全部为圆柱滚子轴承,本文在Hertz接触理论[11]的基础上建立两自由度的局部故障动力学模型,并假设滚子不发生打滑现象。基于Patil[12]假设,将滚子与滚道的接触简化为非线性弹簧—质量系统,如图2所示。
1.2 Hertz接触力计算
基于Hertz非线性接触理论,Harris等[13]推导出了非线性载荷与位移的关系。
F=Kδn
(1)
式中:K为载荷变形系数,δ为径向位移;对于圆柱滚子轴承n=10/9,滚珠轴承n=3/2。航空发动机中介轴承的滚动体为圆柱滚子。中介轴承两个滚道之间的总变形量δ为两个滚道分别与滚动体之间的法向变形量之和。
δ=δi+δo
(2)
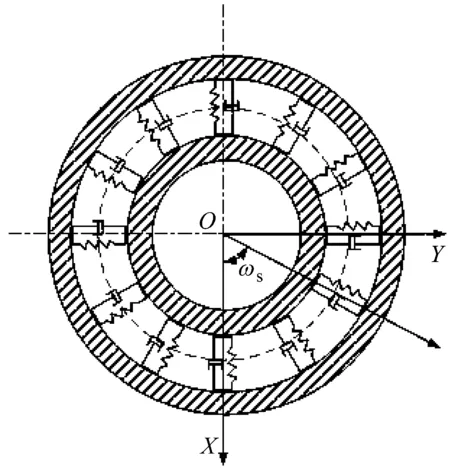
图2 基于Patil理论的假设模型
于是,可得
(3)
式中:δi和δo为内、外圈与滚动体之间的法向变形量;Ki和Ko为内、外圈与滚动体之间的接触刚度。对于圆柱滚子轴承有Kl=8.06×104l8/9。
图3为本文所研究中介轴承的简化模型。图中,第i个滚子与X轴的夹角为θi,其变形量δ为
δ=xcosθi+ysinθi-Cr
(4)
式中:x和y为轴承沿X轴和Y轴的位移;Cr为滚子和滚道之间的初始径向间隙。
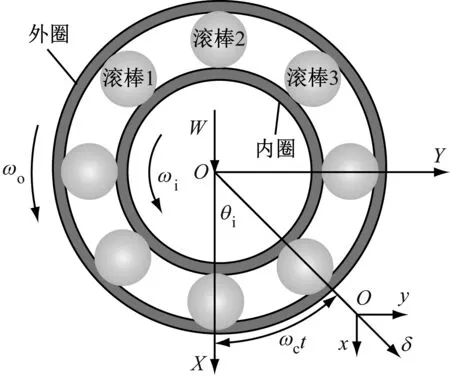
图3 中介轴承简化模型
(5)
(6)
式中:ωi、ωo和ωc分别为中介轴承内、外圈和滚动体的角速度;θt0为相对于X轴第一个滚子的初始夹角;Z为轴承滚子个数,d为滚子直径,Dm为轴承节径,α为轴承压力角。将式(4)代入式(1),得到第i个滚子的Hertz接触力为
Fi=K[xcosθi+ysinθi-Cr]10/9
(7)
由此可知,轴承的总体Hertz接触力在X轴和Y轴上的分力为
(8)
1.3 基于弹流润滑理论的接触刚度计算
中介轴承在正常运转过程中一般处于弹性流体动压润滑状态,滚子和滚道之间存在弹流润滑油膜,油膜压力分布情况如图4所示。从图4中可以看出弹流润滑压力曲线和Hertz压力曲线在分布上具有近似性。本文所建立的考虑弹流润滑影响的动力学模型中,将轴承的刚度考虑为油膜刚度和接触刚度的串联刚度[14]。

图4 中介轴承弹流压力分布
本文假设润滑油为恒温且不存在端泄影响,滚子和滚道接触点不发生滑动。采用Dowson- Higginson线接触膜厚公式计算滚子和内、外圈之间的油膜厚度[15],如式(9)所示。
(9)

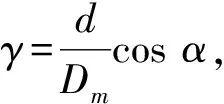
(10)
由于中介轴承为圆柱滚子轴承,轴承压力角α=0,则有
(11)
当量半径为
(12)
式中“-”为内圈与滚子的接触当量半径;“+”为外圈与滚子的接触当量半径。将式(11)代入式(12)则有
R=r(1∓γ)
(13)
将各参数代入式(9)可以求出滚子与内、外圈的最小油膜厚度hi和ho。
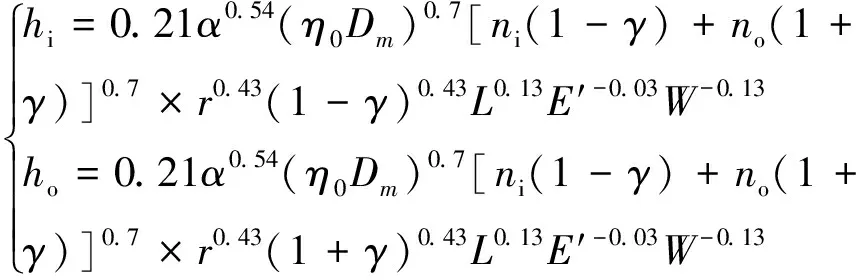
(14)
h=hi+ho=CiW-0.13+CoW-0.13
(15)
式中,Ci和Co分别代表式(14)hi和ho中W-0.13前的系数。
根据刚度定义,由式(15)可求得中介轴承滚动体和内、外圈的油膜刚度为
(16)
根据串联刚度的计算公式可求得滚动轴承在考虑弹流润滑影响的总刚度为
(17)
则式(8)中的刚度K改写为K′。
1.4 时变位移激励
本文主要研究中介轴承早期缺陷形式,且缺陷长度大于圆柱滚子的长度,此种故障的宽度较小,滚子经过缺陷时下降的位移会小于故障的深度,滚子经过缺陷的状态如图5所示。图中H为故障的深度,B为故障的宽度,He为最大的位移激励。由图可以看出,当圆柱滚子进入和经过缺陷时,滚子始终与I边相接触,当滚子接触到II边时,滚子已离开缺陷区。此种经过方式可以采用半正弦函数来描述位移的时变激励。滚子的最大位移激励He为
表3是1980年至2015年在北京举办过个人演唱会的歌手群体及变化情况。从表中可见,近年来,台湾地区歌手在北京个人演唱会市场占有非常大的比重。

图5 滚子经过缺陷状态图
(18)
滚子经过缺陷的时变位移激励函数可以采用以下函数来表示。
(19)
式中:Φd为缺陷的角度;θd0为缺陷的初始角。
缺陷角Φd和第i个滚子与X轴的夹角θi如图6所示。

图6 外圈表面局部缺陷
当缺陷在内滚道上时,
(20)
当缺陷在外滚道上时,
(21)
由于轴承表面存在缺陷,轴承的接触变形量δ需要引入时变位移Hd,式(4)变为
δ′=xcosθi+ysinθi-Cr-Hd
(22)
1.5 动力学微分方程
本文根据刚性套圈的假设理论[16],将中介轴承建立为两自由度动力学系统。将接触刚度、阻尼、Hertz接触力、时变位移和恒定径向载荷W代入动力学方程。
(23)
式中:M为中介轴承质量;c为中介轴承结构阻尼系数;W为轴承所承受径向载荷;x和y为X与Y方向的位移;λ为滚子与滚道是否接触的开关量,表示为

(24)
2 中介轴承局部缺陷模拟实验
2.1 实验设备
为验证模型的准确性,采用双转子试验台进行故障模拟实验。双转子中介轴承模拟实验系统如图7所示。该实验台模拟了某型发动机的支承传动方案,在该支承方案中,4号支点为中介轴承。本文所采用的轴承是SKF nu1004M圆柱滚子轴承。采用线切割的方法在轴承的外圈制造了表面缺陷,缺陷形状如图8所示,方框内为外圈缺陷。在轴承座和机匣的X和Y方向布置4个PCB加速度传感器进行振动数据采集。

图7 双转子中介轴承故障模拟实验系统

图8 外环存在故障的中介轴承
2.2 模型参数
实验过程中,高、低压转子同向旋转,高压转子转速设置为1 000 r/min,低压转子转速设置为625 r/min,实测高压轴为1 001 r/min,低压轴为624 r/min,径向载荷设定为200 N。SKF nu1004M轴承的参数,如表1所示。
在设定转速下,高、低压转子同向旋转,滚动体通过外滚道的故障频率为fbpo=33.55 Hz,滚动体通过内滚道的故障频率为fbpi=47.17 Hz。
2.3 故障特征提取
由于中介轴承的结构特点,其信号经过复杂的传递路径才能传递到支座和机匣上,因此采集的中介轴承振动信号信噪比较低。本文采用多尺度形态滤波和小波降噪相结合的方法对实验原始信号进行降噪处理。外圈故障中介轴承的时域信号和包络谱如图9和图10所示。

图9 外圈缺陷中介轴承实验数据时域图

图10 外圈缺陷中介轴承实验数据包络谱图
从图9可以看出,中介轴承外圈存在缺陷时,其时域信号存在明显的冲击成分,且脉冲的强度存在周期性的变化,这是由于滚动体经过缺陷的冲击受到轴转频或保持架转频调制的原因。从图10中可以清晰的看出,实验测得的中介轴承外圈故障频率为33.02 Hz,该频率与经验公式计算的故障频率33.55 Hz相比存在误差,这是由于在实验过程中轴承存在打滑现象。图中同时存在通过频率的2倍频和3倍频。
3 模型验证
3.1 模型与实验结果分析
本文采用改进的Newmark-β法[17]对建立的运动微分方程(式(23))进行动力学求解。当γ=1/2,且β=1/4时,该方法具有二阶精度,是一种无条件稳定的方法。
当缺陷位于中介轴承外滚道时,通过本文建立的模型求得的振动时域信号和包络谱如图11和12所示。

图11 外圈缺陷中介轴承模拟数据时域图

图12 外圈缺陷中介轴承模拟数据包络谱图
从图11中可以看出,轴承振动的时域信号存在明显的周期冲击成分。从图12中可以看出,本文所建模型的仿真包络谱与实验包络谱图基本相似,同时出现了通过频率1至4倍频,且幅值依次递减。动力学模型求得的故障频率为33.57 Hz,与通过经验公式计算的频率33.55 Hz基本相同,由此证明了本文建立的带局部缺陷的中介轴承动力学模型的有效性和准确性。
3.2 弹流润滑影响分析
为了研究弹流润滑对计算结果的影响,本文对不同缺陷尺寸下的有、无润滑的轴承振动响应进行了仿真。
图13和图14表示的是缺陷尺寸为0.1 mm时,有、无润滑的轴承振动信号的包络谱图。从图中可以看出,在缺陷尺寸相同时,中介轴承有润滑时其振动要小于无润滑的中介轴承,这是由于存在润滑时,润滑油对轴承起到了阻尼减振的作用。
本文计算了缺陷尺寸从0.1 mm变化到4 mm时,中介轴承在有润滑和无润滑情况下的振动响应。中介轴承在两种状态下振动加速度变化趋势如图15所示。从图中可以看出,两种状态下中介轴承的振动加速度都随着缺陷尺寸的增加而呈上升趋势。在同样缺陷尺寸下,无润滑轴承振动加速度要高于有润滑轴承,这是润滑油膜具有一定的阻尼减振作用。在缺陷尺寸小于1 mm时,随着缺陷尺寸变大,中介轴承振动加速度增加较快,而有润滑中介轴承振动加速度明显低于无润滑轴承,这是由于缺陷尺寸较小,油膜的减振效果作用较为明显。当缺陷尺寸继续增大时,有润滑轴承的振动加速度上升也很快,这是由于缺陷尺寸已经很大,润滑油膜很薄,减振作用效果降低。

图13 缺陷0.1 mm时无润滑中介轴承包络谱图

图14 缺陷0.1 mm时有润滑中介轴承包络谱图
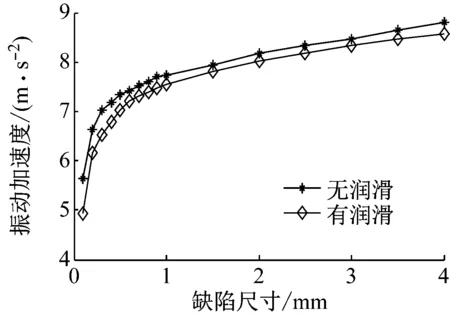
图15 不同缺陷时有润滑和无润滑中介轴承振幅
4 结 论
(1)本文建立了一种考虑弹流润滑影响和时变位移激励的局部缺陷中介轴承动力学模型,该模型对局部缺陷中介轴承的数值模拟结果更加精确。
(2)采用双转子实验系统开展了带局部缺陷中介轴承的故障模拟实验,并将实验结果与数值模拟进行对比,验证了建立动力学模型的准确性和有效性。
(3)采用所建立模型模拟了不同缺陷尺寸下,有、无润滑时中介轴承的振动响应。对比分析结果表明:随着缺陷尺寸增大中介轴承的振动响应呈增加趋势,且有润滑轴承的振动小于无润滑轴承的振动。
