基于扩张状态观测器的轧机振动抑振器研究

王鑫鑫, 闫晓强

(北京科技大学 机械工程学院，北京 100083)

随着国民经济快速发展，不论是在数量还是在质量上对薄带钢的需求逐年增加。然而，制约薄带钢生产的关键因素之一就是轧机振动问题。轧机振动是一种机电液界耦合的“幽灵”式振动，轻则在带钢和轧辊表面产生振痕，重则发生断带和爆辊等严重事故。

目前现场针对轧机振动的抑振措施主要是调节轧机参数的抑振方法，发挥了重要作用，例如安装振动阻尼器[1]，提高磨辊质量[2-3]，调整乳化液润滑特性[4-5]和机械间隙调整[6]等。也有学者采用先进优化算法，例如神经网络和遗传算法等，对轧机工作状态参数进行优化设计，成功降低了颤振，提高了轧制速度[7]。被调节的轧机参数主要包括轧机等效刚度、等效阻尼以及激振力，但是其效果需要经过繁杂的试验验证，找到最佳参数。

随着控制理论日趋成熟，主动抑振方法逐渐引起重视。此方法不必要探究振因和振源，省去了繁杂的现场试验。Schlacher等[8]采用非线性微分平坦理论，对机架间的活套位置和工作辊的转速进行控制，进而实现对机架间张力的控制，通过仿真验证了抑制颤振的有效性。Yang等[9]论述了轧制过程、轧机机械结构和液压系统，以厚度控制为目标，考虑垂直振动的影响，使用定量反馈理论设计控制器，有效地提高了鲁棒性、抗外扰的能力和厚度控制精度。许宝玉[10]鉴于引起轧机振动因素的不确定性，依据统计学原理和最优控制理论建立随机最优控制器，以工作辊振动加速度的统计特性-均方值为控制目标，将最优控制力加在工作辊和支承辊之间，大幅度的降低了工作辊加速度的均方值。凌启辉等[11]采用改进粒子群优化方法，以振动加速度有效值和动态响应为双优化目标，对PI控制器参数进行寻优，缓解了轧机振动。

本文提出一种轧机振动抑振器，其工作原理为：提取原控制器输出信号和压下缸位移信号中的振动信号为抑振器的输入，将振动外扰和内部不确定参数视为总和扰动，利用扩张状态观测器(ESO)估计总和扰动，然后将总和扰动转化为伺服阀的等效输入，实现轧机抑振控制。仿真结果表明，抑振器针对三种经常出现的轧机耦合振动现象均具有良好的抑振效果。

1 轧机振动耦合模型

为了方便问题研究，将轧机振动耦合模型做如下简化：①只考虑垂直振动，不考虑扭转振动；②认为上辊系与下辊系关于轧制中心线对称，并且轧制中心线静止不动；③将带钢从耦合模型中分离出来，带钢和工作辊之间的相互作用用轧制力表示；④机架简化成刚体；⑤认为压下缸位移和支撑辊位移相等。

针对某四辊轧机建立轧机振动动态耦合模型，工作原理，如图1所示。

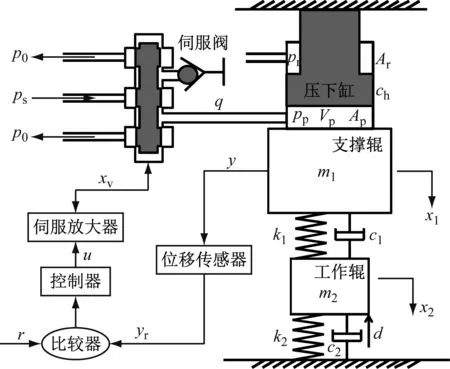
图1 轧机耦合振动简图

(1)

其中

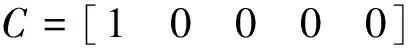
其中，yr为测量输出；u为控制器输出电压；xv为伺服阀阀芯位移；q为伺服阀输出流量；pp为活塞腔压力；Ap为活塞面积；x1为支撑辊位移；Vp为活塞腔体积；ch为压下缸内泄漏系数；pr为有杆腔背压；Ar为有杆腔有效截面积；x2为工作辊位移；m1为支撑辊等效质量；c1为支撑辊与工作辊之间的等效阻尼；k1为支撑辊与工作辊之间的等效刚度；m2为工作辊等效质量；c2为工作辊与带钢之间的等效阻尼；k2为工作辊与带钢之间的等效刚度；d为轧制力；y为实际输出，即支撑辊位移；ps为油源压力；p0为油箱压力；kp为控制器比例系数；ka为伺服放大器比例系数；kq为滑阀流量增益；kc为滑阀流量-压力系数；βe为油液弹性模量；ks为位移传感器的比例增益。

2 扩张状态观测器原理

韩京清[13]首次提出了扩张状态观测器(ESO)的概念，其核心思想是把模型误差和外部扰动看作总和扰动，并将其扩张成一个系统状态，利用观测器估计系统所有状态，然后将被估计出来的总和扰动补偿到系统输入端，使系统被补偿成一个标准型[14-16]。目前，ESO已经得到了广泛应用，例如机器人系统中柔性连接的轨迹跟踪[17]、永磁同步电机的运动控制[18]、高压共轨喷射系统的压力控制[19]和加筋板的振动控制[20]等。

考虑如下n阶系统

(2)

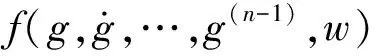
令b=b0+Δb，b0是b的估计值，Δb代表b的不确定性偏差，定义gi=g(i)(i=1,2,…,n) 和gn+1=f+Δbu作为系统的n+1个状态，则可对式(2)设计如下状态观测器

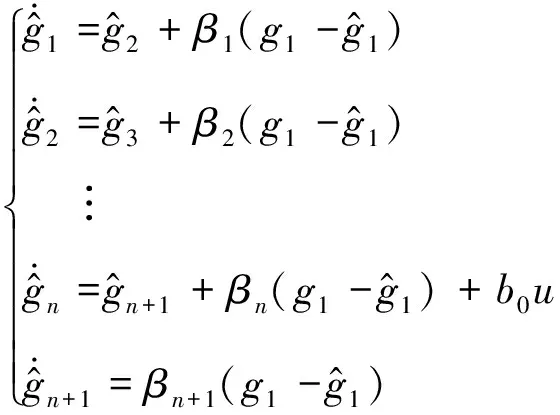
(3)

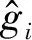
3 抑振器设计

因为研究核心是抑制振动问题，而且压下系统中存在着许多补偿回路，为了避免抑振器对主回路和其它补偿回路产生较大影响，抑振器的输入经过处理获得振动信号，其输出带有限幅功能。

抑振器主要包括四部分：信号滤波前处理、扰动估计、扰动补偿和输出限幅。其工作原理的方框图如图2所示。

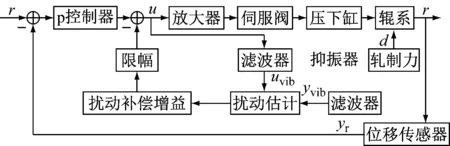
图2 抑振器工作原理方框图

令u=uvib+uval，yr=yvib+yval和B=[B1,B2]，则式(1)可改写成

uvibG-dG′=yvib

(4)

uvalG=yval

(5)

其中G=C(sI-A)-1B1；uvib为与振动相关的系统输入；uval为与振动无关的系统有效输入；yvib为与振动相关的系统输出；yval为与振动无关的系统有效输出；G′=C(sI-A)-1B2。

式(4)为由扰动引起的轧机振动部分动力学方程，式(5)为无外扰时轧机动力学方程。信号前处理的目的是将式(4)和式(5)区分开来，其方法为用滤波器来提取系统输入和系统输出信号中的振动主频信号，即uvib和yvib。

接下来对式(4)设计扩张状态观测器估计系统中的振动外扰和参数不确定性。

在正常轧制过程中，轧机振动系统所受的外扰是谐波形式，而且振动频率的大致范围也是可以确定的，但是谐波的相位和幅值是完全未知的，所以外扰的部分信息可以被用来设计ESO。考虑谐波外扰模型， 同时，假定式(4)中k2存在参数不确定性，可得系统模型为

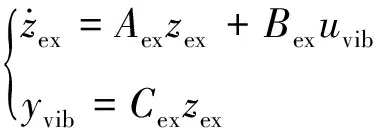
(6)

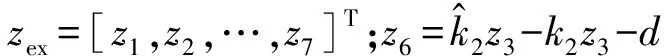
对式(6)设计ESO，状态空间方程如下

(7)

其次设计扰动补偿增益，将总和扰动转化为伺服阀等效输入。

然而系统中的扰动是不匹配扰动，被估计出来的总和扰动并不能在系统内部被抵消，但是它可以在输出通道中被补偿[21-22]。因为工作辊的振动是主要被考虑对象，所以通过在工作辊位移通道中补偿总和扰动的方法来抑制工作辊的振动。

令式(6)中z3=0，可得抑振控制量usup和总和扰动z6之间的关系为

(8)

又因为G(s)是物理不可实现的，所以还需要串联一个低通滤波器

(9)

式中，T为低通滤波器系数。

至此，已获得扰动补偿增益的传递函数为F(s)G(s)。在原系统中加入抑振器之后，控制量输入为

(10)

式中，u0为原控制器输出。

4 仿真结果及分析

为了验证所提出方法的有效性，对比系统中接入抑振器和未接入抑振器时的振动速度幅值。在Matlab/Simulink中使用“状态空间”模块搭建系统模型以及扰动估计环节，使用“LTI System”模块调用“工作空间”中扰动补偿增益环节的传递函数，利用m语言设定系统模型和抑振器的相关参数值。系统模型参数设定，如表1所示。

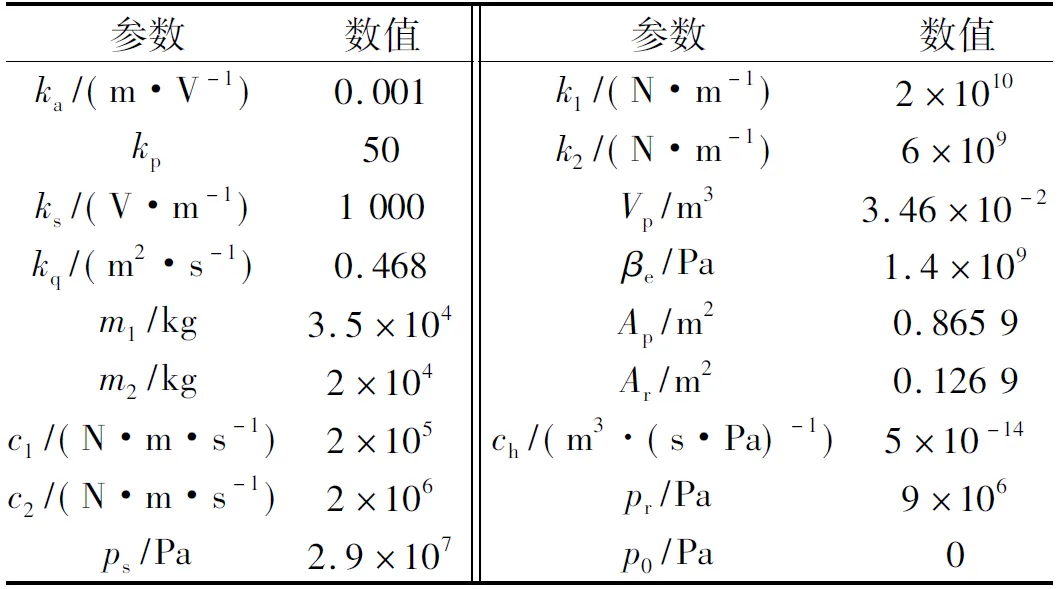
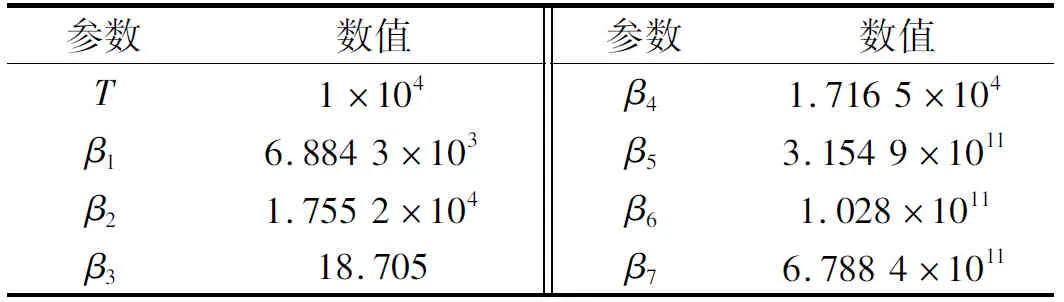
虽然ωo越大，ESO对扰动的估计能力越强；T越大，抑振器的相位滞后越少，从而使抑振器的抑振能力越强，但是因为现实中的噪声干扰等因素，ωo和T的取值是有限制的，不能太大。因为在正常轧制过程中，经常出现固定的单一集中频率、频率相近的多个集中频率和频率随速度变化的情况，所以下面分别针对这三种情况做仿真分析。

4.1 单一频率情况

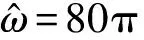
根据图3和图4中投入抑振器前后的振动幅值对比可以看到，工作辊振动几乎完全被抑制了，幅值从原来的4.6 mm/s下降到抑振后的0.06 mm/s。

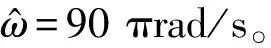
图3 工作辊振动速度时域图

图4 工作辊振动速度频域图

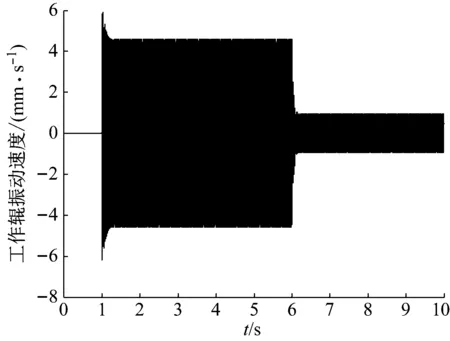
图5 工作辊振动速度时域图

从图5和图6中可以看到，工作辊振动速度幅值从抑振前的4.6 mm/s下降为抑振后的0.94 mm/s，降幅约为80%。虽然获取的外扰频率存在偏差，抑振器依然得到了非常可观的抑振效果。由此可以得出，抑振器具有良好的鲁棒性能。

4.2 多频率情况

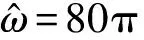
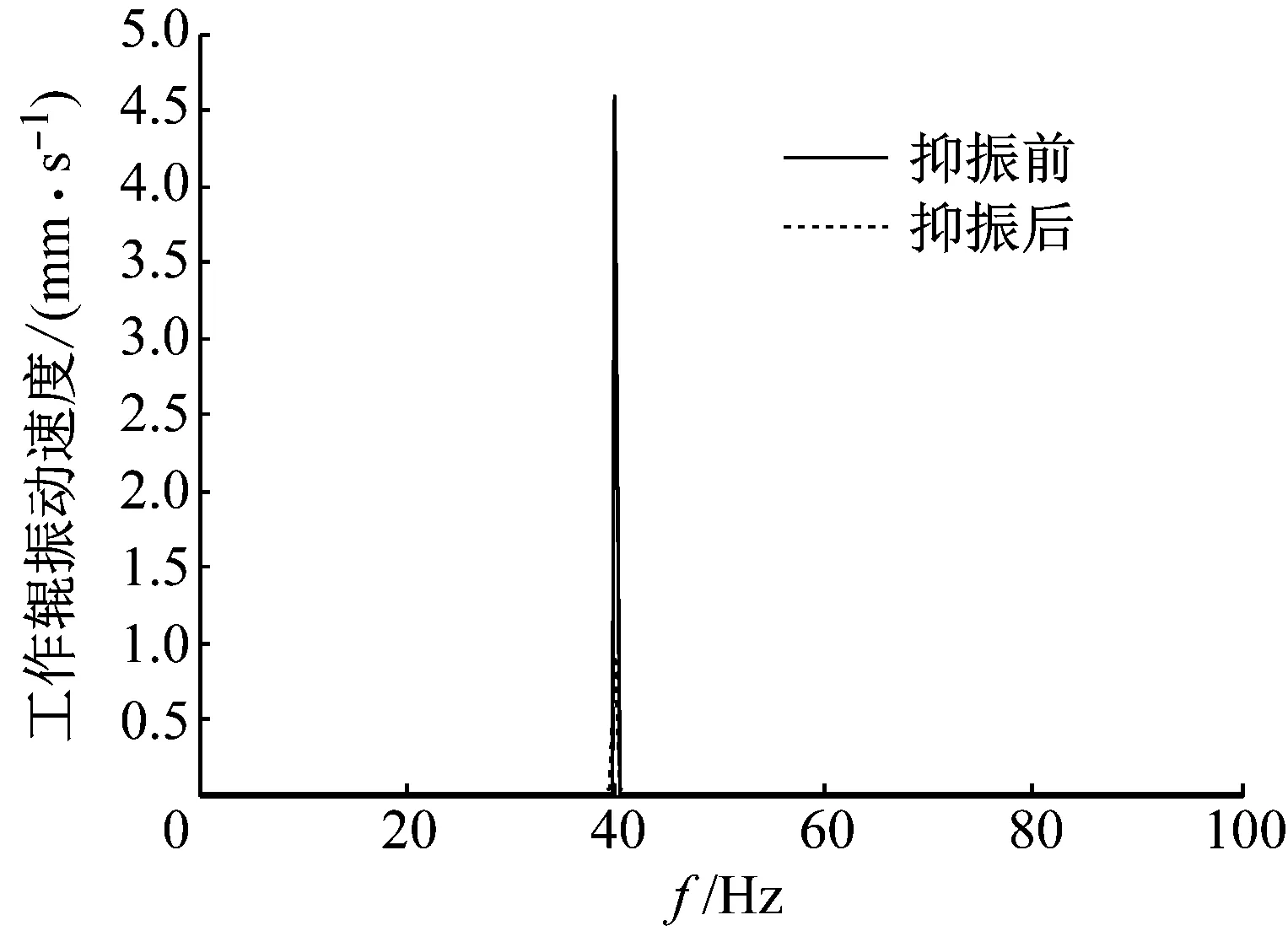
图6 工作辊振动速度频域图

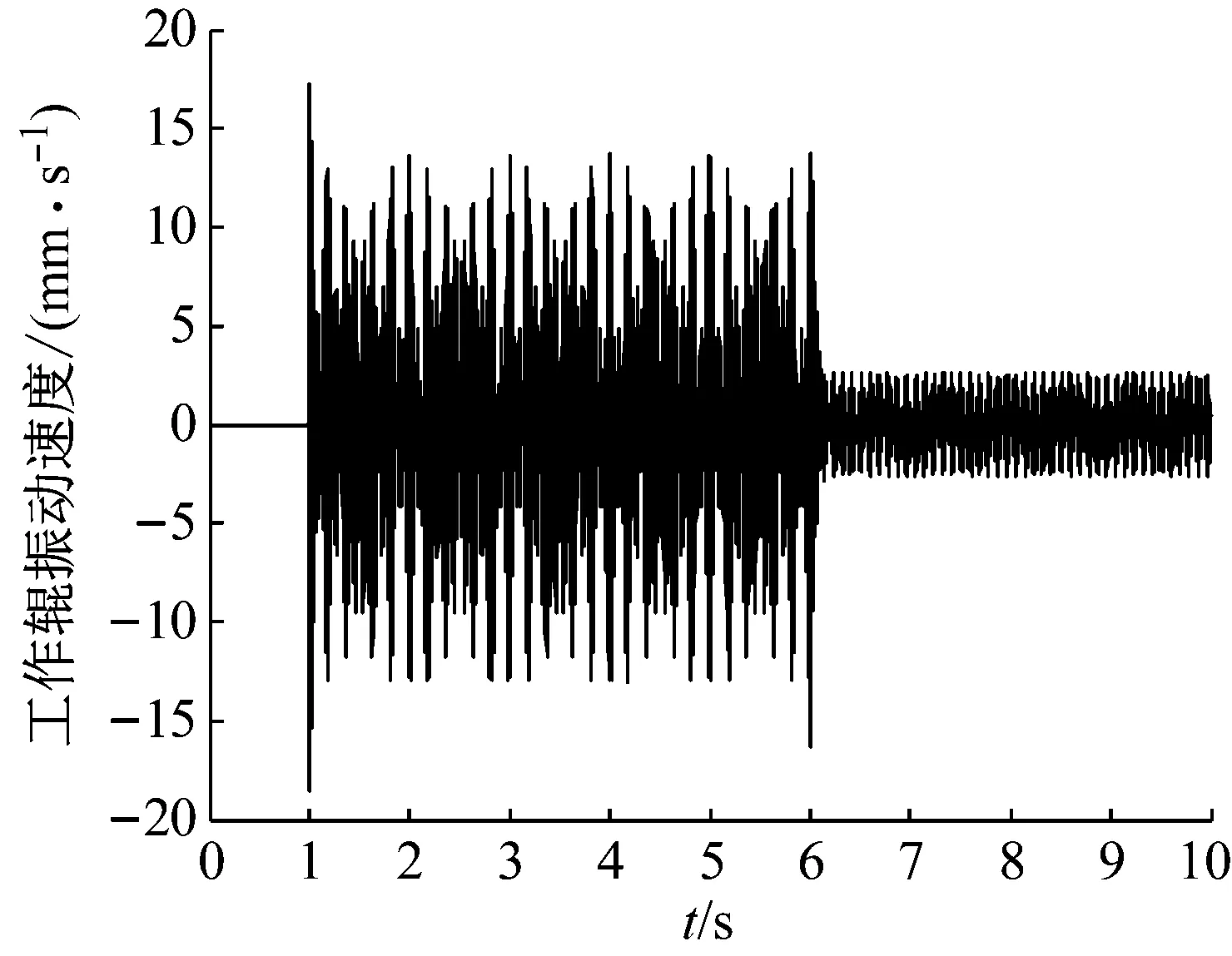
图7 工作辊振动速度时域图

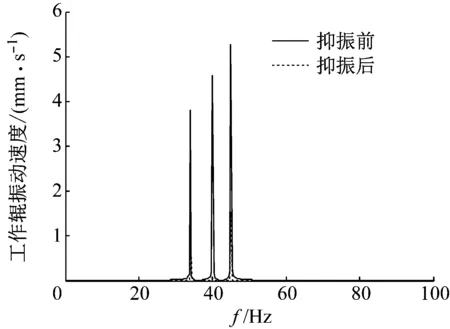
图8 工作辊振动速度频域图

从图7中可以看出，最大振动速度幅值从13.5 mm/s降至2.5 mm/s。从图8中可以看到，34 Hz的振动，幅值从3.8 mm/s降至1.1 mm/s，降幅约为71%；40 Hz的振动，幅值从4.6 mm/s降至0.07 mm/s，几乎完全被抑制；45 Hz的振动，幅值从5.3 mm/s降至1.5 mm/s，降幅约为71.7%。由此可以看出，针对多频率并存的振动，抑振器依然具有良好的抑振效果，而且频率越接近抑振器中设定的扰动频率，抑振效果越明显。

4.3 变频率情况

图9 工作辊振动速度时域图

从图9中可以看出，投入抑振器之前，随着外扰频率的增加，振动幅值增大。投入抑振器之后，在8.5 s时振动幅值最小，几乎为0，此时的外扰频率为40 Hz；而在向前或向后偏离8.5 s时，因为实际振动频率与抑振器仿真设定的振动频率之间的偏差，振动幅值出现逐渐增大的趋势。而且投入抑振器后比投入抑振器前振动幅值出现了明显的下降。在投入抑振器前后的时频图图10和图11中也得到同样的结论。

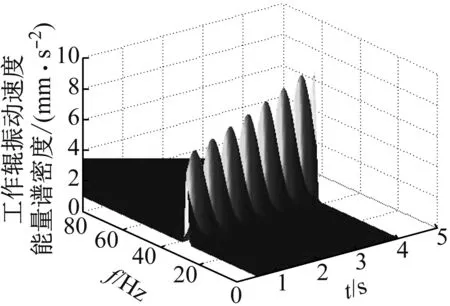
图10 工作辊振动速度时频图(抑振前)

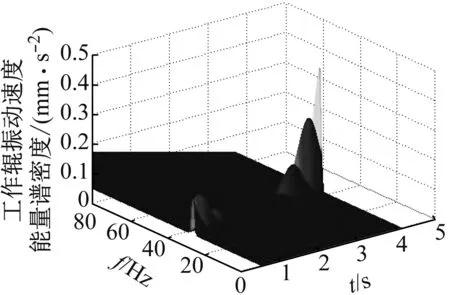
图11 工作辊振动速度时频图(抑振后)

5 结 论

以某热连轧机F2为研究对象，建立了机电液耦合振动模型。提出了基于扩张状态观测器来设计附加模块嵌入到液压压下系统中的抑振器来抑制轧机振动的思想。针对轧机振动中经常出现的三种情况：单一频率、多频率和变频率振动现象，分别做了仿真研究和分析。仿真结果表明：设计的抑振器可以有效抑制多种情况下的轧机振动，为解决和抑制轧机振动提供了一种新的途径。