基底悬摆隔震结构振动台试验研究
2019-03-23胡宇飞张会会罗检文何燕青
鲁 亮, 胡宇飞, 张会会, 罗检文, 何燕青
(同济大学 结构防灾减灾工程系,上海 200092)
常规意义的悬挂结构如图1所示,最早在桥梁工程中应用,现代悬索桥、斜拉桥也是典型的悬挂结构?。随着悬挂式楼盖结构的出现,它开始应用于大跨建筑领域和高层建筑领域,如德国慕尼黑的宝马总部大楼和香港汇丰银行总部大楼等建筑[1]。本文研究的基底悬摆隔震(Base-suspended Pendulum Isolation, BSPI)结构与一般悬挂结构有不同的结构技术特征,结构示意如图2所示,上部结构通过刚性吊杆(或柔性吊绳)悬挂于刚性基础上,形成单摆结构,利用单摆结构自振周期较长的特点,远长于一般地震波卓越周期,从而达到隔离地震、减小结构地震响应的目的。与图1类似的悬挂结构由主、子结构构成,其结构振动控制原理类似TMD控制技术,需要同时考虑主、子结构的抗震性能。BSPI结构悬挂在刚度很大的基础上,没有主、子结构的概念,其隔震原理类似橡胶支座隔震结构。基于现代结构振动控制方法,BSPI结构的技术特征在于:①BSPI结构可以通过调整吊杆(吊绳)的长度来改变整体结构的动力特性,从而调整结构地震响应,这里的吊杆提供竖向承载力,重力分量充当整体结构水平向恢复力;②在悬挂层内设置耗能减震装置来控制结构的位移响应,合理设置的阻尼参数可以达到对加速度和位移响应双控制的目标;③利用BSPI结构的构造特点,在吊杆(吊绳)处设置竖向减震弹簧和耗能阻尼器,将竖向隔震与悬摆水平隔震结合起来,使得结构具有三向隔震能力。

图1 悬挂结构示意图
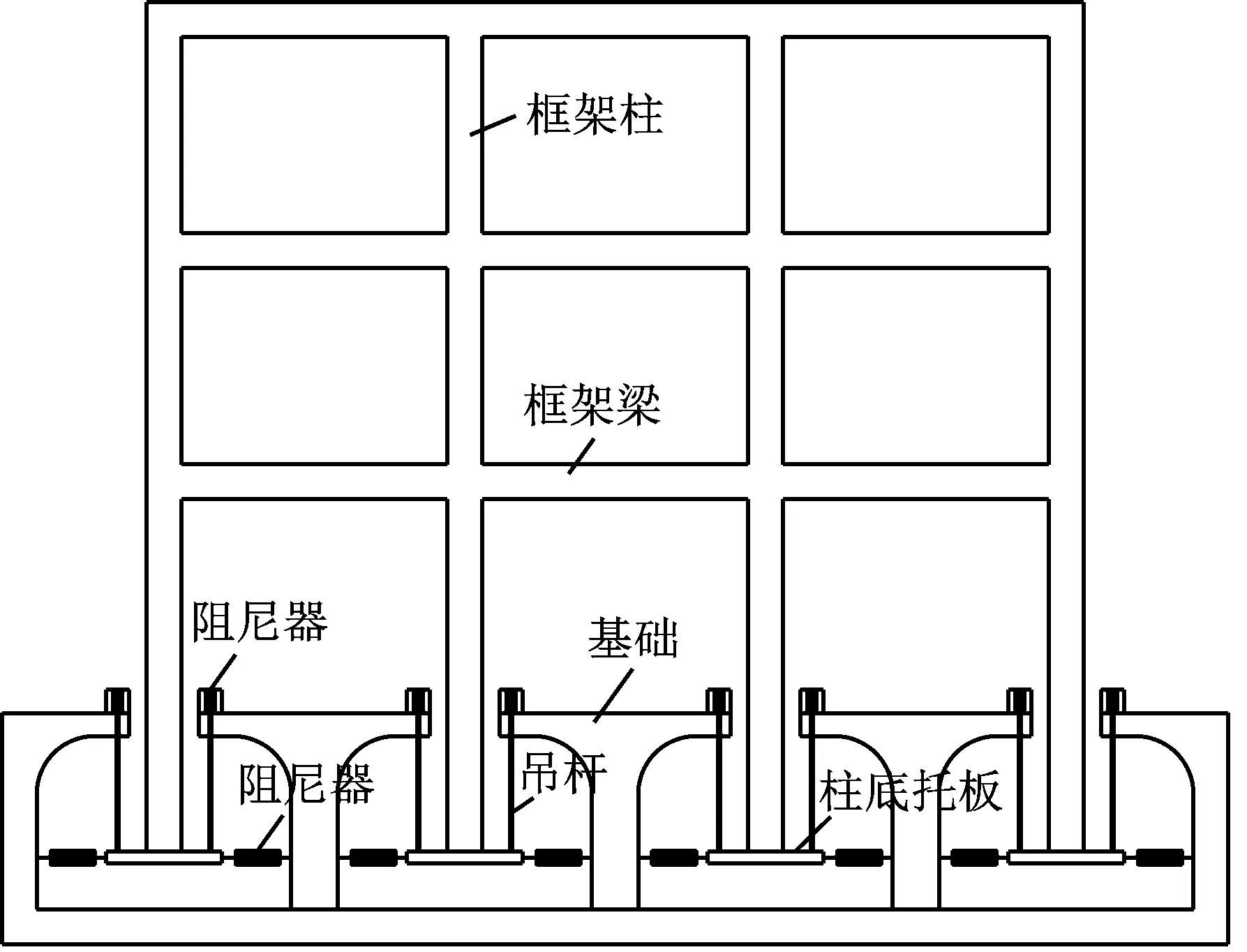
图2 基底悬摆隔震结构示意图
目前关于BSPI结构的研究文献较少,但是利用悬挂隔震的理念古而有之,例如墨西哥人早期就设计了悬挂柱子底部的框架结构房屋[2]。1948年泽连科夫[3]提出通过房屋和地基之间的柔性连接,把地震时产生振动的结构物看作悬摆结构,保证结构在地震作用下保持不坏状态,并首次于1959年在阿什哈巴德建造的一座三层民房上加以应用,但是泽连科夫研究的悬摆隔震结构不具备现代结构控制技术的基本特征。1995年,Bashsiha等[4]提出了悬挂摆隔震(SPI)系统,通过将上部结构安装在悬挂摆板上,达到隔震的目的,其基本周期可以由单摆的振动周期确定,Bashsiha等所进行的试验模型很小,同时不具备竖向隔震能力。王开才等[5]对悬摆隔震结构的力学模型作了等效处理,并研究了常规计算程序对其进行动力分析的有效方法。陈志华等[6]对于对称悬挂在两个支点的钟摇做了解析的和试验的研究,并以平移摆动为例子,得出了悬于两点的摆体结构动力性能。然而,以往研究多集中在基于单摆原理上的隔振研究,随着现代结构控制理论的发展和技术应用,需要赋予基底悬摆隔震技术更多内涵。本文BSPI结构在已有研究的基础上,着重研究了以下三方面的内容:①结构地震动力响应控制,吊杆长度和隔震层阻尼可对加速度和隔震层位移进行双控制的效果;②利用BSPI结构特征,设置竖向振动控制装置,对竖向地震响应进行控制;③进行了大型模型振动台试验,并结合数值模拟分析,综合研究BSPI结构的隔震性能。
1 BSPI振动台模型试验方案
1.1 试验原型与相似关系
试验原型结构为3层框架结构,平面尺寸13.5 m×13.5 m、层高3.3 m、总质量约为600 t,所在场地类别为Ⅱ类,地震设防烈度为8度(0.2g),设计地震分组为第一组。根据原型结构的尺寸、振动台台面尺寸、吊装重量等参数,确定模型长度相似常数为SL=1/5,弹性模量相似比和加速度相似比均为1。
对于BSPI结构,当上部结构的等效层间抗侧刚度大于隔震层等效刚度20倍时,可以采用质量块简化模型进行振动台试验[7]。
1.2 原型结构竖向动力特性
对于一般建筑物而言,竖向振动基本周期很小,通过减小竖向刚度从而达到减小竖向加速度地震响应的难度很大。然而,对于大跨度和长悬臂结构而言,其竖向基本周期较大,很多工程案例的前几阶周期里都有竖向周期,部分网壳结构的前十几阶周期甚至都为竖向周期,因此对于大跨度和长悬臂结构而言,竖向地震作用对结构抗震性能的影响相对更加突出,结构抗震设计时必须加以考虑。同时根据《建筑抗震设计规范》[8]第5.1.1条第4款的规定:8度、9度时的大跨度和长悬臂结构及9度时的高层建筑,应计入竖向地震作用,且8度、9度时采用隔震设计的建筑结构,应按相关规定计算竖向地震作用。所以本文竖向隔震研究以此类大跨度和长悬臂结构为对象。
作者收集了35个典型大跨度和长悬臂结构竖向振动基本周期数据,经统计分析,竖向一阶自振周期平均值约0.50 s,并以0.50 s作为本文原型结构竖向振动的自振周期[9]。具体做法是将1.1节所述原型结构放置在选定刚度的弹簧上,构成竖向隔震的原型结构。
1.3 结构振动控制(隔震)措施
依据反应谱理论,当结构自振周期变长,超出地震波卓越周期范围外,结构的加速度响应会减小、位移响应会变大。
在水平方向设置悬摆隔震层,通过调节悬吊杆的长度,就可以调整结构振动基本周期,从而调整结构水平向减震系数。在竖直方向采用设置减震弹簧来加大结构竖向自振周期,从而减小结构竖向地震响应。
在减小结构恢复刚度、减小结构加速度响应的同时也会增大结构位移响应,而结构位移响应也是需要控制的抗震性能指标之一,一般通过增大结构阻尼来控制,设置阻尼器是增加结构有效阻尼的常用技术,BSPI结构通过设置黏滞阻尼器来控制结构位移响应。为了节约结构布置空间,作者将竖向隔震弹簧和阻尼器整合成“一种穿心式竖向减隔震装置”,并获得了专利授权[10]。
1.4 BSPI结构抗震设防目标
结构控制技术是提升结构抗震性能的有效手段,甚至可以达到大震不坏的韧性结构(Resilient Structure)的要求。结构抗震设计的两个重要指标是地震响应加速度和位移,与橡胶支座隔震结构类似,经过隔震参数设计的BSPI结构的隔震层上部结构的地震设防承载力要求可减低一度至一度半。
BSPI结构上部结构的层间位移响应很小,结构在罕遇地震作用下一般处于弹性状态,位移响应集中在隔震层。由于BSPI结构是新型隔震结构体系,隔震层位移限值无规定,参考FM365的有关规定[11],建议BSPI结构隔震层在罕遇地震作用下位移角性能目标设定为1/20,同时设定结构竖向变形的位移限值为吊杆长度的2%。
1.5 BSPI结构自振频率理论公式
通过以上对BSPI结构布置的描述,BSPI结构的力学模型如图3所示。其中质量块m(图3构件1)和A类弹簧(图3构件5)模拟未经隔震的原型结构,此结构具有0.5 s的竖向自振频率。当不考虑竖向隔震、同时水平位移未加控制时,结构动力特性与单摆结构相同。当考虑竖向隔震时,吊杆长度(摆长)会随着结构竖向变形的产生而变化,对结构自振周期的影响需要加以评估。

1-质量块M;2-吊杆;3-刚性托架;4-水平向阻尼器;
原型结构竖向振动固有频率
(1)
式中:kA是模拟悬挑或大跨结构竖向自振周期所需的弹簧刚度,见图3中的构件5(A类弹簧);m是结构总质量,见图3中的构件1。
图3所示结构振动系统为典型弹簧摆振动系统,系统有两个自由度,分别为径向(竖向)和切向(水平向)。
系统动能和势能分别为
(2)
(3)
拉格朗日函数
(4)
分别列出两个自由度r、θ的的拉格朗日方程为
(5)
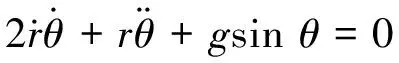
(6)
当摆角、竖向位移均为小量时,式(5)、(6)可简化为[12]
(7)
(8)
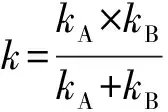
从式(7)和(8)可以看出,结构竖向振动和水平向振动在小振幅运动(控制位移)下可以解耦,这样包含竖向隔震的BSPI结构的隔震机理十分明晰。
2 BSPI振动台试验
2.1 试验模型
为了验证BSPI结构的抗震性能,振动台试验按多模型、多工况开展,试验模型按仅考虑水平向、仅考虑竖向、考虑三向以及是否有阻尼器控制(有控或无控)排列组合。振动台模型所采用的动力相似关系见表1,试验系列内容见表2。
依据原型参数和表1的试验相似关系,BSPI结构模型利用一个4.8 t(=600/125)的质量块来模拟有一定重心高度的上部结构(为模型制作方便,本次试验对重心高度的相似要求予以放松)。



模型设计时,采用4个相同的A类弹簧支撑上部结构,每根弹簧的刚度约为946 N/mm。进行竖向隔震设计时采用串联B类弹簧来降低结构固有频率,通过试算将结构减震系数落到预期取值范围内,得到隔震后的原型结构固有周期设计为1.75 s,是隔震前的3.5倍。采用式(1),计算得到隔震后模型的竖向刚度为
利用公式
(9)
计算得到单根B类弹簧刚度约84.1 N/m。在计及上部结构下支撑的刚度后,最终B类弹簧刚度取为110 N/m。
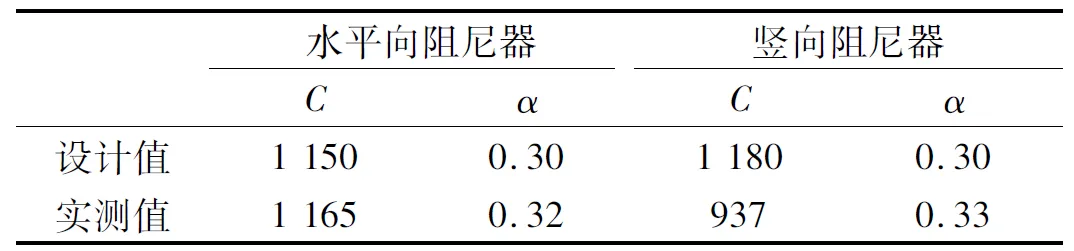
根据规范《圆柱螺旋压缩弹簧》GB-T 2089—2009[13],选取质量块下A类弹簧型号为YB35×170×340/4.5圈-右旋,刚度为946 N/mm,承载力为58.6 kN,可用最大变形量为87 mm;选取隔震用B类弹簧型号为YB30×220×700/8.5圈-右旋,刚度为108 N/mm,承载力为28.5 kN,可用最大变形量为324 mm。竖向隔震采用黏滞阻尼器来控制结构的竖向位移并消耗地震能量。经试算采用的竖向黏滞阻尼器参数为C=1 180 N/(m/s)0.3,α=0.30,设计行程为±50 mm,最大阻尼力为0.613 kN。
三维隔震BSPI振动台模型的平面图和正视图如图4、图5所示,模型照片见图6。
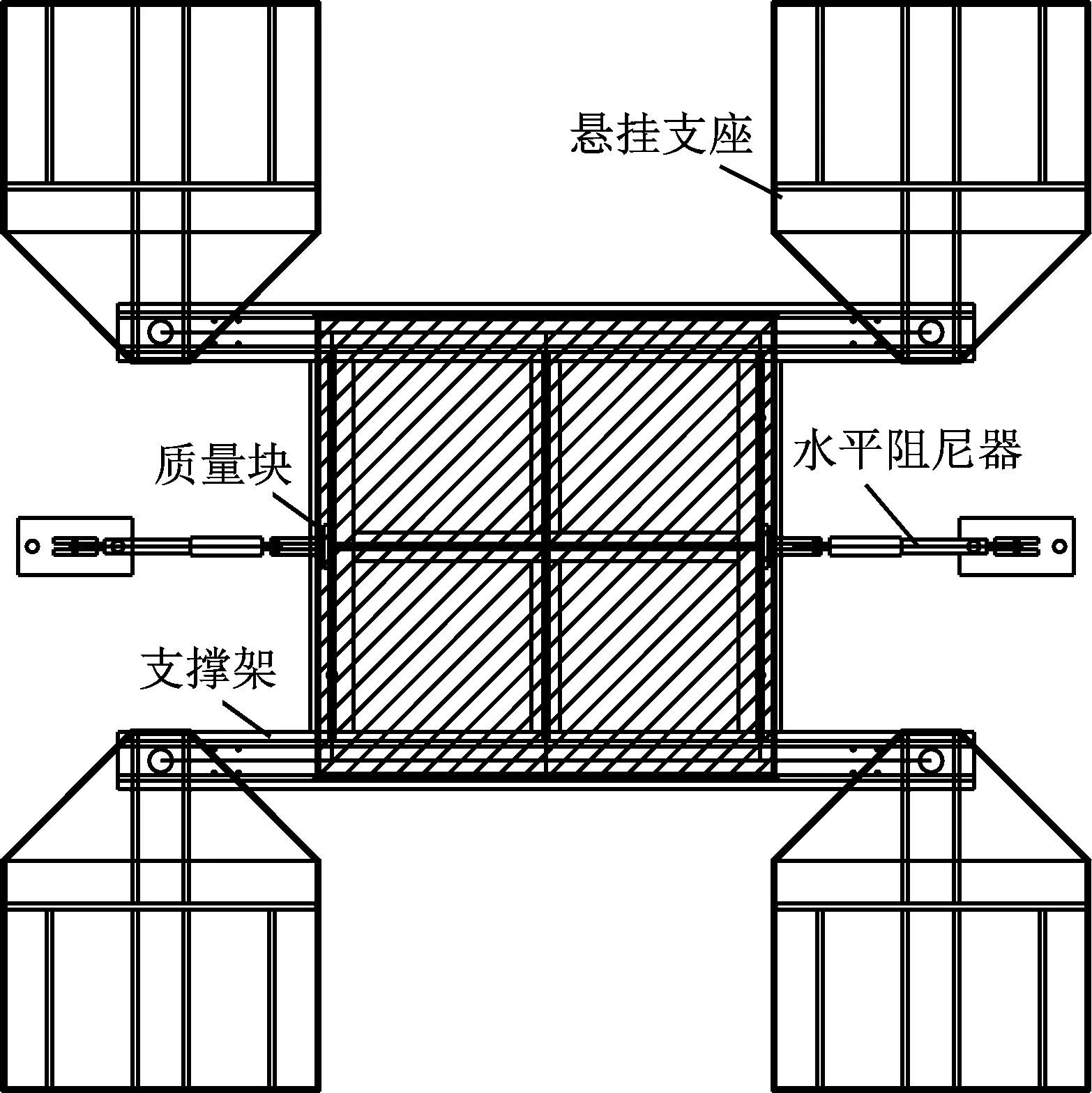
图4 三维隔震BSPI结构模型平面

图5 三维隔震BSPI结构模型正视
2.2 弹簧和阻尼器性能测试
为了提供计算模型减震弹簧和阻尼器力学参数,对两种阻尼器和两种弹簧进行了性能测试。
黏滞阻尼器的力学性能测试采用MAS-100型电液伺服作动器,作动器最大出力100 kN,行程250 mm,最大速度33 mm/s。考虑到MAS-100型作动器最大加载速度不能满足测试要求,利用杠杆原理放大6倍行程加载,见图7。

图6 BSPI振动台试验模型

图7 黏滞阻尼器试验加载装置
根据不同加载频率作用下的阻尼力测试结果,推导出黏滞阻尼器的阻尼系数C和速度指数α,其结果如表3所示。
弹簧的力学性能测试采用YE-2000型压力试验机,测试得到的A、B类弹簧的线刚度如表4所示。

2.3 试验过程
试验过程为先采用白噪声对模型结构进行扫频,再由小到大输入不同能级的天然地震波。依照表2所列的试验系列变更安装试验模型并重复以上两步。
水平单向、竖向和三维BSPI结构模型对应的振动台地震波输入分别为X向、Z向和X、Y、Z三向。根据试验设计,振动台试验选用El Centro地震记录和Taft地震记录作为振动台台面激励。
试验时根据相似关系对输入的地震波进行1/倍的时间轴压缩,根据各种工况下的加速度峰值对输入的地震波峰值进行相应的调整,从而生成不同工况所需要的台面激励波形。
以安装有黏滞阻尼器的水平单向BSPI结构模型为例(表2中系列7),加载工况和顺序如表5所示。

2.4 传感器测点布置
试验时需要测量的内容有:结构的动力特性,结构的加速度响应(单向/三向),结构的整体位移响应(单向/三向)。对于水平单向BSPI结构模型,加速度传感器和整体位移计均布置2个,分布在质量块的侧面。对于三维BSPI结构模型,在X、Y两个方向布置各布置4个加速度传感器和2个位移传感计,在Z方向布置4个加速度传感器和4个整体位移计,分布在质量块的侧面和顶面。
3 试验结果
BSPI振动台试验得到大量试验数据,通过试验初步验证了采用BSPI结构体系隔震的可行性及其优异的隔震效果。限于文章篇幅,此处仅列出部分BSPI水平隔震相关的试验数据。
3.1 水平单向BSPI结构模型地震响应
3.1.1 结构模型动力特性分析
通过白噪声对无控和有控结构模型进行扫频试验,得到模型的初始频率、阻尼比和振型。
白噪声扫频分析结果表明:
(1) 测试得到的无控结构模型的振型为X向平动的,一阶频率为0.75 Hz,且随着输入地震动幅值的增大,频率基本保持不变。理论计算得到的理想单摆的基频为0.5 Hz,说明试验模型提供了附加刚度,经分析主要是吊杆两端球铰提供了部分附加刚度。
(2) 测试得到的黏滞阻尼器有控结构对应的一阶频率为0.875 Hz,说明阻尼器提供了部分刚度。
(3) 输入0.05g白噪声时测得无控结构阻尼比为0.058,安装黏滞阻尼器的有控结构的阻尼比为0.198,说明设置阻尼器使得结构阻尼比显著增大、阻尼效果明显。
3.1.2 有控结构和无控结构的加速度响应
测试得到的地震作用下有控BSPI结构(有阻尼器)和无控结构的加速度最大响应对比情况如表6所示。

从表中可以看出,BSPI结构加入黏滞阻尼器后,结构加速度响应相对于无控结构变化不大,主要原因在于BSPI结构设置阻尼器后有两方面的作用,一方面增设阻尼器后结构刚度会有所增加,加速度响应加大;另一方面,增设阻尼器后,结构有效阻尼增加,带来的效果是加速度响应减小。但总的来说,BSPI结构的加速度响应比非隔震结构要小很多(本文质量块模型的非隔震结构加速度响应接近振动台台面输入)。另外,从测试数据看出,BSPI结构对Taft地震波的隔震效果更好。
3.1.3 有控结构和无控结构的位移响应
结构模型的相对位移为结构相对于振动台台面的相对值。表7为BSPI结构在单向地震作用下各工况的相对位移响应最大值。由于模型结构吊杆长度为1 m,所以位移角取层间高度为1 m时的换算值。
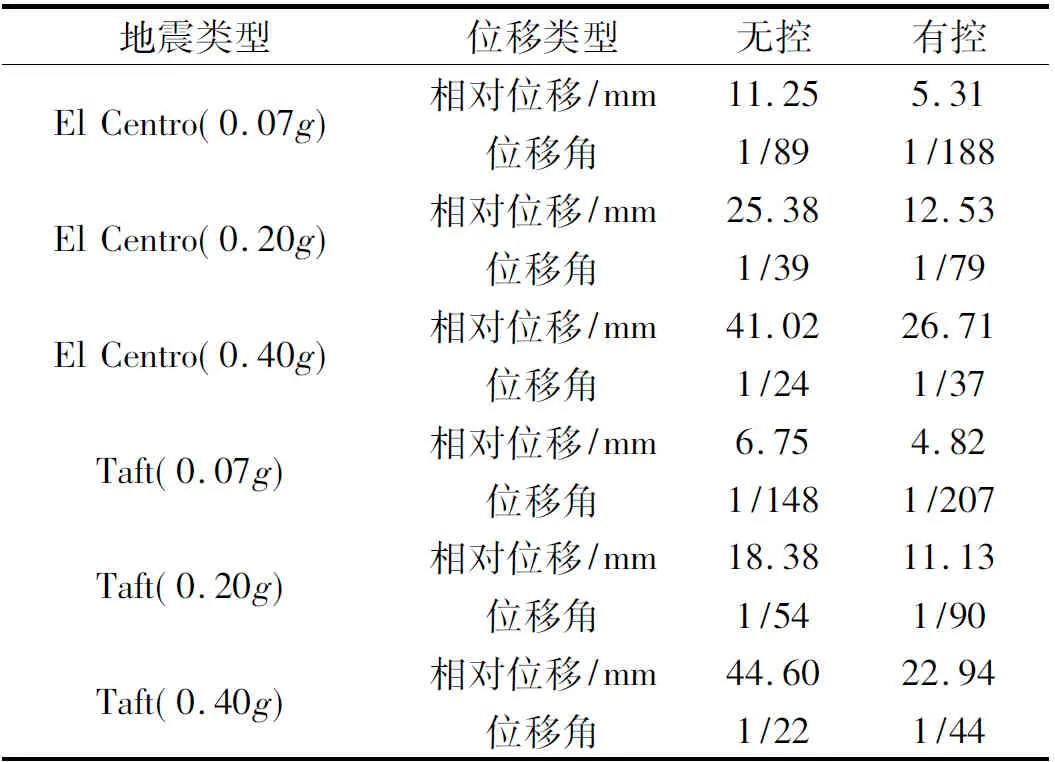
从表7结果可知:
(1)无阻尼器时,BSPI结构位移较大,但也满足大震下位移角小于1/20的要求,这主要是试验前对吊杆球铰存在较大摩擦阻尼估计不足,后期计算分析时考虑了实测的结构阻尼。
(2)当加入黏滞阻尼器后,BSPI结构的相对位移明显减小,几乎为无控结构的一半左右,说明设置黏滞阻尼器能起到良好的位移控制效果。
3.1.4 水平单向BSPI结构模型吊杆内力响应
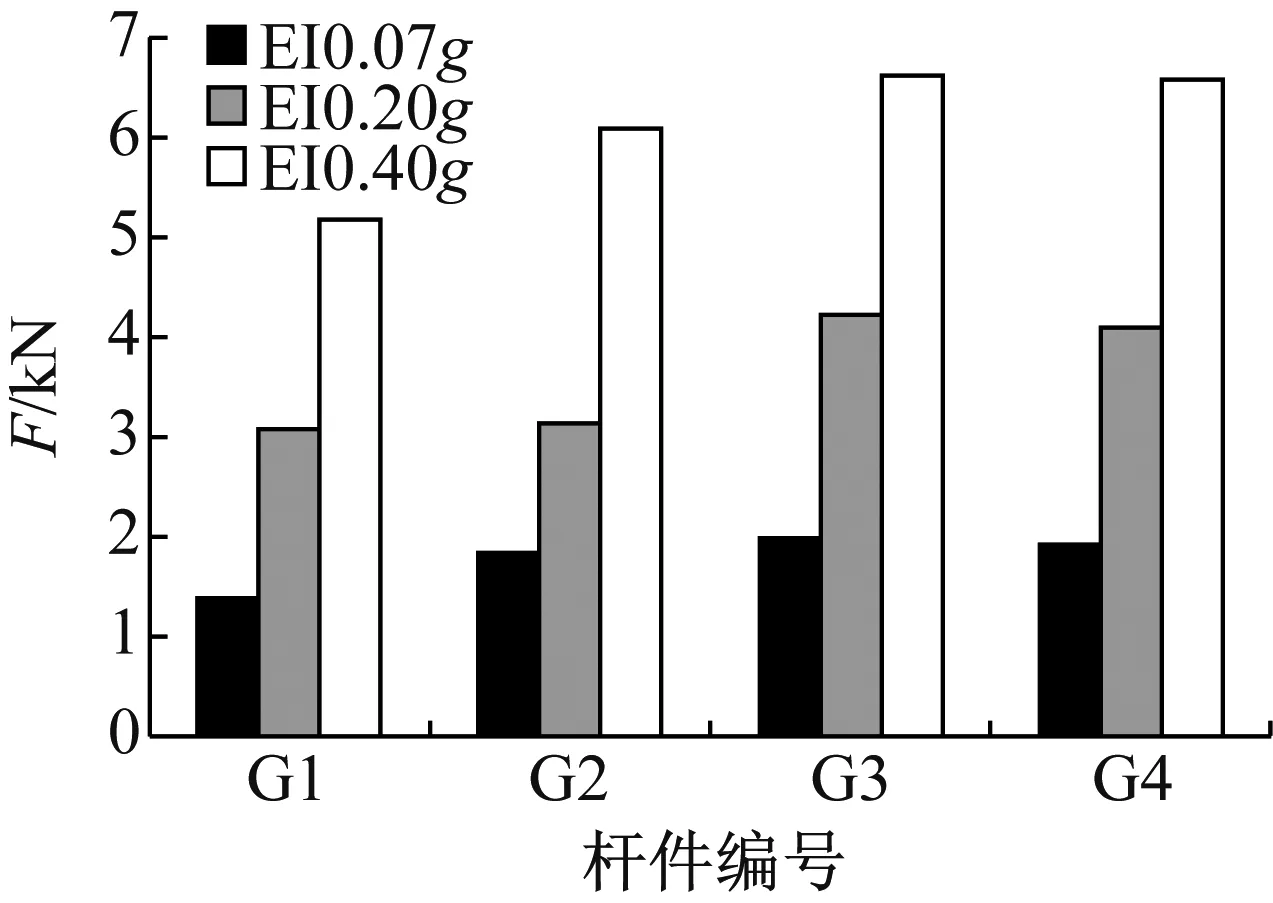
水平单向试验中为了研究结构倾覆力矩对吊杆内力的影响,在吊杆上粘贴应变片,来测量吊杆内力在各工况下的内力变化情况。以El Centro波为例,有控结构和无控结构的吊杆最大内力变化值如图8所示。
(a)无控结构

(b)有控结构
从图8可以看出,随着地震动输入加速度的增大,杆件最大内力变化值不断增大;在同一地震动工况下,安装阻尼器结构的杆件内力变化值明显地小于无控结构,说明设置阻尼器能减小结构整体位移,从而减小了吊杆内力变化值。同时也可以看到,4根吊杆在同一加载工况下,内力变化值略有不同,可能原因是质量块偏置以及地震波正负峰值大小绝对值不同。
3.2 三维BSPI结构模型地震响应
3.2.1 模型结构动力特性
采用0.05g白噪声对结构进行三向扫频分析,得到动力特性,并与水平单向BSPI结构模型的动力特性对比结果列于表8。
从表8可以看出,三维BSPI结构模型的X向和Y向的振动频率和阻尼比基本保持一致,说明三维模型X向和Y向具有基本相同的动力特性。通过与水平单向有控结构扫频结果对比可以知道,X向的阻尼比和频率基本相同,说明Z向的隔震措施基本不影响水平向动力特性,水平向和竖向运动可以解耦。

3.2.2 模型加速度响应
不同水准地震作用下三维隔震模型最大加速度响应见表9。P1、P2、P3、P4分别为X、Y方向上的四个加速度测点。
由于非隔震结构(质量块)在水平向近似刚体,地震作用下的加速度峰值响应近似台面输入。为了更加直观地阐述三维BSPI结构在三向地震作用下的水平隔震性能,将Taft 0.4g三向地震作用下,模型结构水平向加速度响应与振动台台面加速度响应对比时程曲线如图9所示。

(a)X向加速度响应

(b)Y向加速度响应
隔震后的三维BSPI结构模型在三向地震作用下水平向加速度响应明显减小,在设防地震作用下,其减震系数均小于0.4,满足《建筑抗震设计规范》(GB 50011—2010)关于隔震后上部结构抗震构造降低一度设计所对应的隔震系数的要求,说明BSPI结构具有良好的水平向隔震性能。
3.2.3 模型位移响应
结构模型的位移为结构相对于振动台台面的相对值。表10为三维BSPI结构模型和水平单向BSPI结构模型在单向地震作用下各工况的相对位移响应最大值对比结果。D1~D4为各位移测点。

表10 模型最大位移响应
通过单向BSPI结构模型在单向地震作用下X向位移响应峰值与三维BSPI模型在三向地震作用下X向位移响应峰值对比分析可知:
最大位移响应符合设计预期,三维BSPI结构模型在三向地震作用下,位移响应比单向激励下稍小,主要是水平两方向之间的相互影响引起。另外,三维BSPI结构模型中的竖向隔震措施对水平向位移响应影响也比较小。
4 试验结果与计算结果对比
4.1 有限元模型建立
为便于同振动台试验结果作对比,采用ABAQUS软件建立了BSPI振动台模型的有限元分析模型,如图10所示。
模型中吊杆和基础刚性梁均采用钢材,等效质量块采用混凝土材料,用B31单元模拟基础梁和吊杆,基础梁截面刚度EI=2.822×104kN·m2,吊杆为直径30 mm的圆钢。采用Solid单元模拟等效质量块,质量块质量4 800 kg。采用Springs/Dashpots单元模拟结构模型重力恢复刚度和实测结构有效阻尼,结构模态阻尼比的实测值在地震波峰值为0.2g和0.4g时分别取0.074和0.089。采用无转动刚度Hinge连接单元模拟吊杆与基础梁的铰接连接。
限于篇幅,本节给出对无控水平单向BSPI结构模型进行各种工况下的弹塑性时程分析结果。分析时输入的地震波为振动台台面实际输入的地震波,部分有限元模拟工况见表11。
4.2 加速度响应对比
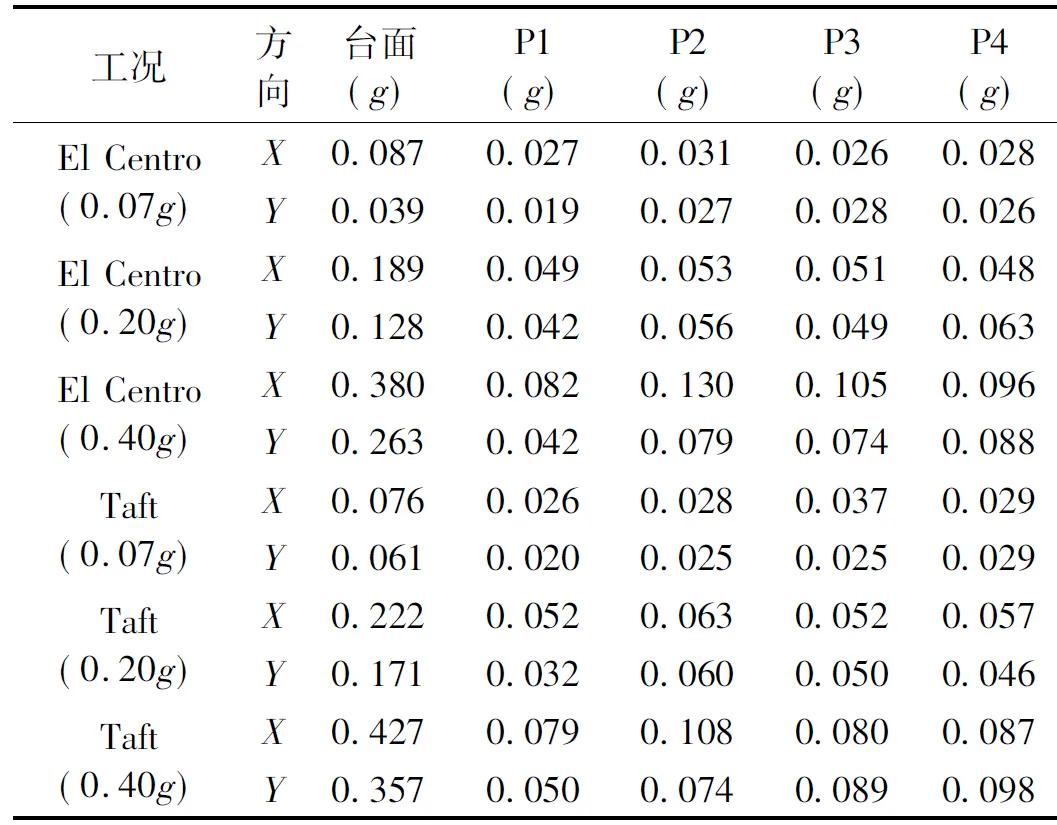
以El Centro波为例,设防地震和罕遇地震作用下无控BSPI结构模型的振动台试验数据和有限元分析的加速度响应对比如图11所示。


(a) El Centro 0.20g
(b) El Centro 0.40g
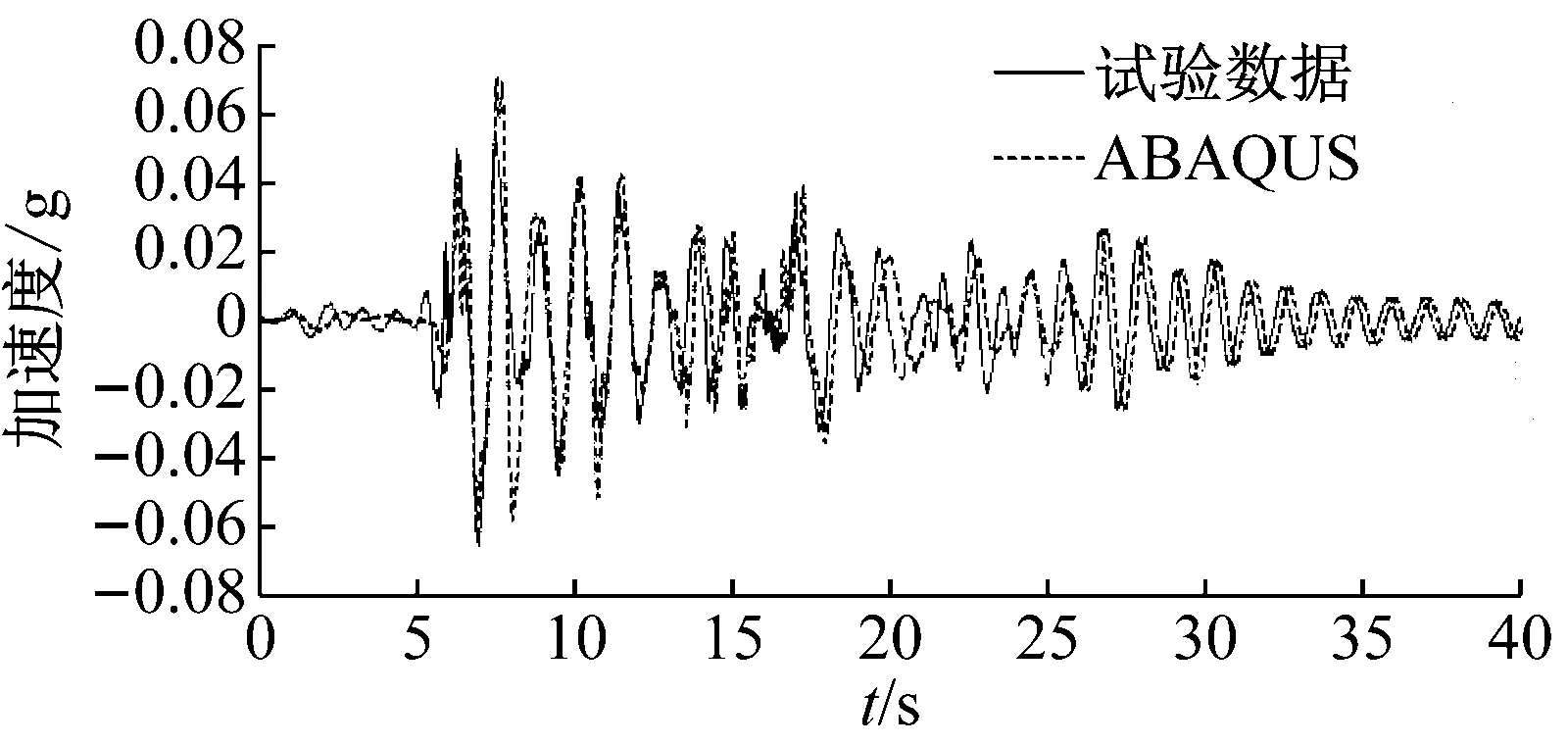
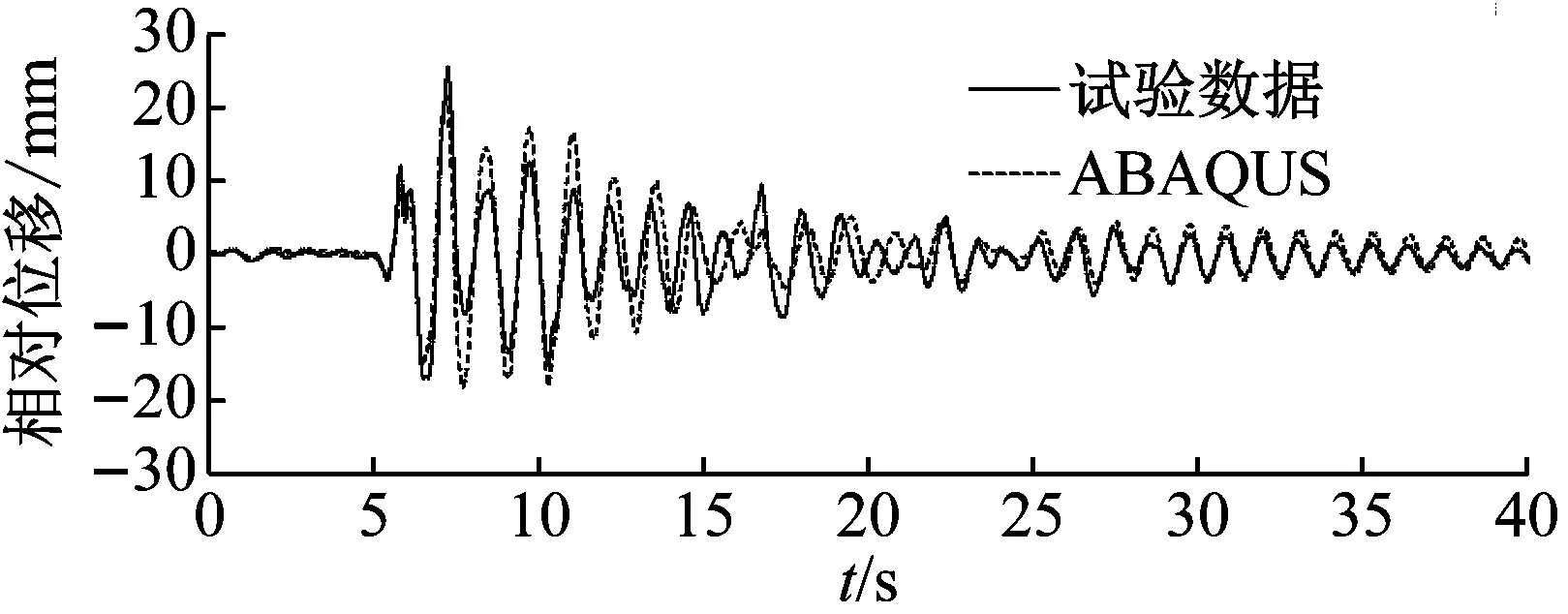
4.3 位移响应对比
以El Centro 波为例,设防地震和罕遇地震作用下无控BSPI结构模型的振动台试验数据和有限元分析的位移响应对比如图12所示。
(a) El Centro 0.20g
(b) El Centro 0.40g
从数值模拟和试验数据的对比可知,结构层间位移与加速度时程波形和峰值均能吻合良好,说明利用ABAQUS建立的有限元模型正确,节点力学模型和非线性分析方法选择合理。
5 结 论
本文通过水平单向和三向的振动台试验,并结合数值模拟,研究了BSPI结构在地震作用下的隔震性能,得出的结论如下:
(1)利用单质点混凝土质量块模拟上部结构,确定了弹簧和阻尼器的参数和布置、试验工况、测点位置以及输入的地震波,并通过试验得出了阻尼器和弹簧的实际参数。
(2)对BSPI结构竖向隔震措施及模型参数设计进行了阐述,振动台试验验证了BSPI竖向隔震的有效性和可行性,从理论和试验证明了在小振幅振动下,BSPI结构水平振动和竖向振动可以解耦。
(3)根据试验实测参数建立了有限元分析模型,计算得出的无控BSPI结构在设防地震和罕遇地震下的时程曲线与试验数据对比可知,计算结果与试验数据基本一致,验证了有限元建模的可靠性。
(4)经过振动台试验验证,表明BSPI结构具有优异的隔震性能,模型设计过程反映BSPI结构具有工程应用可行性。
