宽弦风扇叶片颤振预测的工程研究

章嘉麟，丁建国

(中国航发商用航空发动机有限责任公司，上海201108)

1 引言

航空发动机压缩部件的颤振多发生于大展弦比、小刚度叶片中，一旦发作，可在极短时间内导致叶片疲劳断裂失效[1]。随着民用航空发动机持续向高效率、高可靠性、高推重比的方向发展[2]，发动机风扇叶片尺寸不断增大，各种新结构和新材料也在风扇叶片上得以应用，如钛合金空心风扇叶片、复合材料风扇叶片等。这些技术在减轻叶片质量、提高推重比的同时，也大大降低了叶片刚度，导致风扇叶片颤振问题更加突出。因此，防止风扇叶片颤振已经成为大涵道比民用航空发动机研制过程中所面临的一个重要问题，发展适用于工程设计的风扇叶片颤振预测方法，对于发动机安全设计、缩短设计周期、节省研制经费[3-4]都具有深远意义。

早期的颤振预测主要采用经验法和半经验法[5]进行。这类方法以相似理论为指导，将大量的叶片颤振统计数据整理成经验性预测准则或经验型曲线，引入工程试验数据，用以预测新设计叶片的颤振稳定性[6]。近年来，由于计算机性能的高速发展和非定常流场模拟技术的日渐成熟，基于CFD的方法逐渐成为颤振预报的主流[7-9]。叶轮机械颤振问题的数值研究方法可分为经典法和耦合法[10-11]两种。经典法通过对叶轮机械结构和气动模型的适当简化，忽略流体与结构的耦合关系，将结构与流体分开求解。常用的经典法有特征值法和能量法，Bendiksen等[12]采用特征值法对多种叶栅颤振问题进行了研究，Hall[13]和He[14]等则用能量法对三维叶片颤振进行了分析。耦合法的流体和结构求解是交互影响的，使得流体与结构求解能够考虑更多的非线性因素。Debrabandere等[15]采用耦合法对某压气机转子叶片在设计工况下的气动弹性稳定性进行了研究。Schoenenborn等[16]采用三维有限元模型模拟叶片，利用Navier-Stokes方程求解流场，研究了压气机在喘振工况下的叶片颤振问题。胡运聪[17]和杨真青[18]等运用耦合法对二维叶栅颤振问题进行了求解，指出振动叶栅中的流动具有较强的非线性特征，与非耦合情况存在较大差异。由于流动的非定常性和求解的复杂性，完全耦合计算过程需要投入大量的资源，国内尚未在工程设计中广泛采用。

某大涵道比风扇叶片在设计中采用了宽弦和复合弯掠等技术，在性能考核试验过程中风扇叶片发生了颤振现象。本文分别基于经验法和数值模拟方法，以发生颤振的风扇叶片为对象进行颤振评估。以期通过对其的分析研究，掌握该类叶片的颤振机理；同时，将计算结果与试验结果进行对比，以验证颤振预测方法的准确性。

2 风扇叶片颤振预估方法

2.1 经验法

经验法[19]包括单参数法、双参数法和三参数法等。对于传统的三参数法，通常只计算单一特征截面的折合速度或折合频率、进口相对马赫数以及气动攻角，并与试验得到的经验曲线族进行比较，判断颤振是否发生。本文采用经过改进的三参数法，选择两个特征截面，对风扇叶片进行颤振分析。计算过程为：选择75%和100%叶高处的两个特征截面，计算1～3阶的75%叶高处的折合速度和100%叶高处的模态振型，分别以折合速度和模态振型为横、纵坐标在经验曲线图上查找得出颤振临界攻角。如果75%叶高处的实际气动攻角小于临界攻角，则叶片稳定；反之，则叶片发生颤振。与传统意义上的三参数法相比，改进后的三参数法增加了叶尖截面的模态振型计算，考虑了叶片尖部的扭转和变形，有利于提高预测精度。

2.2 数值模拟方法

本文在对风扇叶片颤振进行数值模拟预测中，采用基于频域方法的能量法，通过引进合理假设，实现流体和固体的弱耦合[20]，计算量和计算精度都能满足工程需求。假设所有叶片以相同的频率和振幅做简谐振动，相邻叶片的振动相差一个相同的叶片间相位角(IBPA)，计算一个周期内非定常气动力对叶片所做的功。计算使用一方程S-A湍流模型；对流项空间离散采用中心差分+二阶/四阶人工粘性；虚拟时间项积分采用显式(Runge-Kutta)和隐式(LU-SGS)相结合的方法；非定常流动采用非线性谐波平衡方法进行频域模拟；并行计算采用OPENMPI。叶片颤振稳定性使用能量法判据[21]，即在叶片的一个振动周期内，叶片振动系统从外界获得的能量与系统阻尼消耗的能量的正负决定了叶片是否颤振[22]。累积功W的计算公式为：

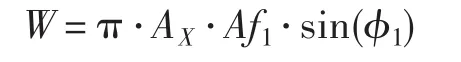
式中：AX为叶片振动位移，Af1为叶片所受非定常力，φ1为非定常力相位角。

3 计算结果及分析

该大涵道比风扇性能试验件，在85%转速外涵逼喘过程中，接近喘振边界时风扇叶片振动超限，图1为监控到的叶尖振幅曲线。可见11号叶片叶尖振幅最大值达到13.61 mm；叶片从32.875 s起振，在35.671 s叶尖振幅达到最大值，历时2.796 s。以该发生颤振的风扇叶片为研究对象，给定85%转速近喘点的工况，分别基于经验法和数值模拟方法，评估叶片的颤振稳定性，并与试验结果进行对比验证。

图1 85%转速外涵逼喘过程叶片叶尖振幅曲线Fig.1 Blade tip vibration amplitude curve during surge at 85%speed

3.1 经验法计算过程及结果分析

3.1.1 计算过程

根据85%转速近喘点工况，首先完成定常气动计算。三维流场计算采用商业软件NUMECA的FINE/TURBO求解。计算设置如下：采用S-A模型；计算域进口按照试验时的真实情况给定总温、总压和进口气流角；风扇内外涵分别给定出口平均静压；固壁为绝热、无滑移边界条件；转静交界面选择为周向守恒型[23-25]。计算网格如图2所示，风扇和外涵出口导流叶片(OGV)的网格拓扑结构为默认的O4H，内涵通道中叶片的网格拓扑结构为HOH。离开叶片表面第一层网格的距离为5 10-6m，y+值保持在10以下。总网格量约300万。

图3和图4示出了计算所得外涵特性线与试验结果对比。可以看到：压比特性的计算结果与试验结果较接近；效率特性方面，由于设计压比较低和受探针测量精度限制，外涵所录取的温升效率较计算结果偏高，但趋势基本一致。取特性曲线中近喘点(图4中蓝色框所示)，将外涵OGV前的总压比和总温比径向分布与级间探针测量结果进行对比，如图5和6所示。考虑到温度测量误差，可认为近喘点的流场计算较为准确。

图3 风扇外涵效率特性Fig.3 Adiabatic efficiency characteristic lines of fan bypass

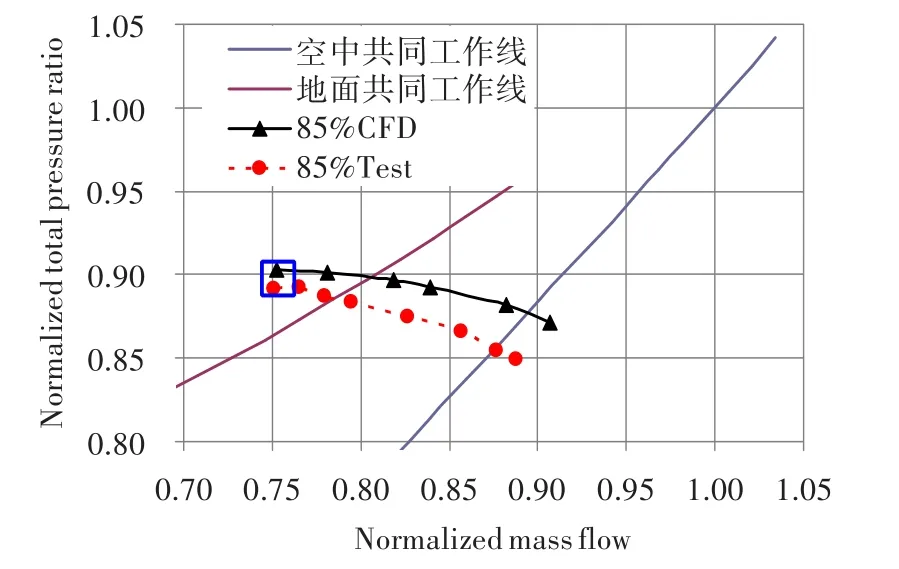
图4 风扇外涵压比特性Fig.4 Total pressure ratio characteristic lines of fan bypass

图5 外涵OGV前总压比Fig.5 Inlet total pressure ratio of bypass OGV

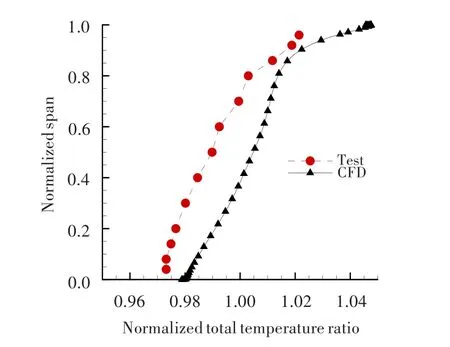
图6 外涵OGV前总温比Fig.6 Inlet total temperature ratio of bypass OGV

其次，完成风扇叶片强度计算。风扇转子为整体叶盘结构，共有18片叶片，其材料为YZ-TC4锻件，表1给出了材料性能参数。叶盘前缘与帽罩用花键连接，叶盘安装边与风扇轴用螺栓连接，轮盘后端面为自由状态。网格单元采用六面体，单元类型为二阶solid186，单元数为114 336，节点数为459 790，建立的有限元模型如图7所示。计算时，施加的边界条件及载荷为：①对风扇盘轴连接法兰(面3)施加轴向和周向位移约束，风扇盘周期对称面(面1、面2)施加周期对称约束；②对风扇盘腔表面施加均布的气动载荷，以模拟腔压对风扇盘的影响；③对风扇整体叶盘施加离心力载荷，对叶身和叶盘流道表面施加气动力载荷，对叶片表面进行气动力插值；④设置分析类型为大变形静态分析进行计算，并在静强度分析基础上进行考虑应力刚化和旋转软化效应的模态分析；⑤在笛卡尔坐标系下，提取计算工况下叶尖前、后缘节点前3阶模态的位移量、比例系数和频率，以及叶尖偏移和扭转变形计算结果。

表1 风扇整体叶盘材料性能参数Table 1 Material properties of fan blisk

图7 风扇转子有限元模型Fig.7 Finite element model of fan rotor

表2示出了风扇叶片前3阶模态下的固有频率。图8为风扇整体叶盘叶身在85%转速外涵喘点状态下的径向变形、轴向变形和总变形分布。由图可知，最大径向变形、轴向变形和最大总变形均出现在叶尖，分别为1.03 mm、-6.64 mm(向后)和8.71 mm。图9为风扇整体叶盘叶身的径向应力、第一主应力和等效应力分布云图。可看出，最大第一主应力出现在叶盆中部区域，为425.19 MPa。

表2 风扇叶片固有频率Table 2 Natural frequency of fan blades

最后，比较颤振临界攻角和实际攻角。具体步骤为：

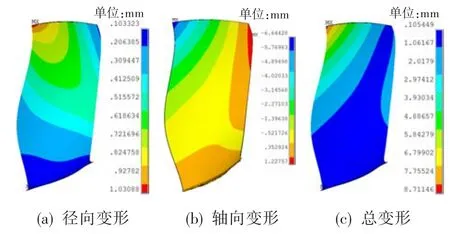
图8 叶身变形云图Fig.8 Deformation cloud diagram of blade

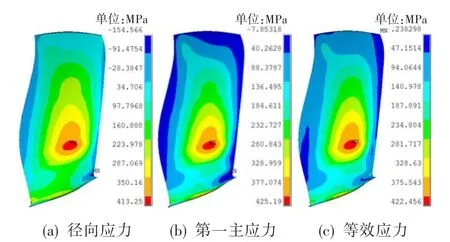
图9 叶身应力分布云图Fig.9 Stress distribution cloud diagram of blade

(2)计算1～3阶模态振型。模态振型的定义为Flap/(φ·B′)。其中：Flap为叶尖弯曲分量，即变形前后叶尖周向偏移量；φ为叶尖扭转角，即变形前后弦线夹角；B′为风扇叶片叶尖弦长。

(3)以折合速度为横坐标，模态振型为纵坐标，在经验曲线图上查出1～3阶的颤振临界攻角。

(4)计算风扇叶片75%叶高处的实际攻角i。i=相对气流角-金属角，相对气流角来自三维计算结果，金属角为叶片造型结果。

(5)比较实际攻角与1～3阶临界攻角大小，若任意1阶的实际攻角大于临界攻角，则叶片发生颤振，反之则稳定。

3.1.2 结果分析

表3示出了风扇叶片的经验法颤振评估结果。可看出1阶模态下，风扇叶片的实际攻角大于颤振临界攻角，评估结果为叶片发生颤振，与试验现象一致。

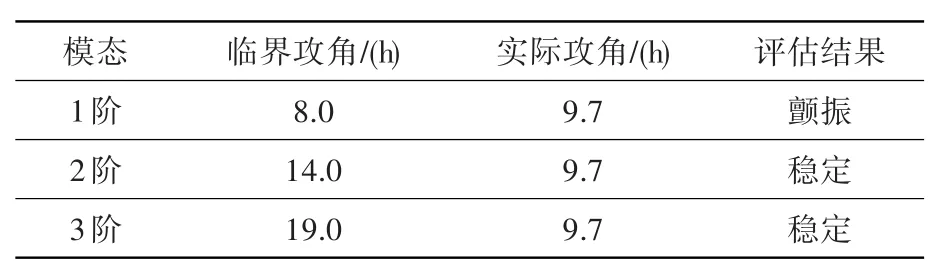
表3 经验法颤振评估结果Table 3 Flutter evaluation results of empirical method

3.2 数值模拟方法计算过程及结果分析

3.2.1 计算过程

颤振数值模拟采用Turbo3D软件。该软件使用频域法进行颤振分析，是一种流固解耦的能量法分析方法。主要计算过程如下：

(1)使用网格转换程序将Numeca生成的网格文件转换为Turbo3D程序可读的网格文件，设定输入边界条件(进口总压、总温、气流角、转速、掺混面模型、湍流模型、CFL数、人工粘性系数、壁面函数、多重网格层数等)、初场文件(各叶片排的压力、轴向速度、切向速度、径向速度、密度等)和交界面设置文件(各交界面位置的径向网格对接点数，出口边界条件等)，完成85%转速近喘点定常计算。

(2)将强度计算得到的风扇模态变形量数据连续插值到CFD网格上，并设置叶间相位角。插值方法为二维线性插值，兼容强度有限元网格中包含的非结构化六面体网格。对于有限元网格上存在的三棱柱网格、四面体网格等非结构化六面体单元，均按照20节点输出的方式，确定单元的外表面。插值原理是使用CFD网格表面的四边形节点的三个点构成单独的三角形面，选取离此三角形质心最近的有限元网格上的点赋值给此三角形的三个节点，以提高插值的准确性。

(3)以定常计算和模态插值结果为输入，采用频域谐波方法进行非定常计算。假设非定常频率是叶片振动自然频率的线性叠加，叶片按预先设定方式、振幅振动。叶片间相位角计算范围为-160.0h～160.0h，对应的节径为-8～8。

(4)计算1～3阶模态下各叶间相位角的累积功，若各模态各叶间相位角的累积功都小于0则叶片稳定，若在某阶模态某叶间相位角的累积功大于0则存在颤振风险。

3.2.2 结果分析

图10为85%转速外涵近喘点前3阶振型对应不同叶片间相位角的累积功随节径的变化特性。如图中红圈所示，对应1阶振型-1、-2节径的累积功大于0，其中最大累积功出现在-1节径，对应为-20.0h叶片间相位角。根据能量法判据，该风扇叶片存在颤振风险，与试验现象一致。

图11为最不稳定点节径-1时叶片表面的气动功(气动功沿表面积分即为累积功)分布，上图为吸力面，下图为压力面。可以看到，在吸力面叶尖激波位置处出现气动功峰值。通过减弱叶尖激波强度以减小当地的气动功，从而减小1阶的累积功，抑制颤振风险。

图10 前3阶振型对应不同节径的累积功Fig.10 Worksum of different nodal diameter for the first three mode shapes

图11 节径-1时风扇叶片表面气动功分布Fig.11 Fan blade surface worksum distribution with the nodal diameter equals to-1

4 结论

基于经验法和数值模拟方法对发生颤振的风扇叶片进行了颤振预测计算分析，得到如下结论：

(1)三参数法和数值模拟方法的分析结果均表明叶片发生颤振，且与试验结果一致。两种方法的计算量均在可承受范围内，工程上具备实用价值。

(2)根据三参数法的预测结果，可通过以下手段降低叶片颤振风险：减小近外涵喘点风扇叶片中上部叶高处的气动攻角，增大叶片1阶频率，增大叶片75%叶高处弦长并减小100%叶高处弦长，减小叶片尖部扭转角。

(3)数值模拟方法的分析结果表明，叶片中上部激波位置处气动功出现峰值。通过减小喘点风扇叶片攻角，改善流动状态，以及减弱叶尖激波，可以有效降低颤振风险。