篦齿结构磨损对封严性能的影响

袁紫琪，宁方飞

(北京航空航天大学能源与动力工程学院，北京100191)

1 引言

航空发动机内部转静子间的封严对发动机性能至关重要，封严技术的改进和泄漏流量的降低是未来航空发动机性能提高的一个关键[1-2]。篦齿封严结构因可在高温、高转速下正常工作，且具有良好的可靠性，已广泛应用于航空发动机转静子封严中。

在篦齿封严实际工作过程中，常因篦齿和衬套涂层的碰磨导致二者发生几何改变，进而对封严性能造成较大影响。此外，篦齿封严加工过程中，齿尖处受加工精度和加工设备的影响通常会出现一个小的倒圆，而该倒圆也将造成蓖齿结构封严性能变化。国内外研究人员针对蓖齿封严开展了多项研究工作。国外，Zimmerman等[3]对光滑直通齿进行了研究，通过简化衬套磨损结构发现带磨损槽的衬套将降低篦齿的封严性能，但其泄漏流量比等间隙下的直通齿结构的泄漏流量小。Andrea等[4]研究了齿尖前缘倒圆对篦齿内部流动及其封严性能的影响，结果表明齿尖前缘倒圆对封严性能有不利影响。国内在该领域的工作主要集中在篦齿齿数、齿腔厚度/齿尖间隙值及齿腔形状对封严性能的影响。纪国剑[5]、胡东旭[6]通过实验获取了直通齿沿流动方向的压力损失规律，结果显示沿流向的第一个齿和第二个齿间压力损失最大，之后几个齿的压力损失较小，表明只靠增加篦齿齿数来提高封严性能的成效不明显。吴丁毅[7]采用实验手段研究了一个篦齿齿数为3的直齿和斜齿在不同齿腔厚度/齿尖间隙值下，其泄漏系数随压比的变化。结果表明，对于直齿，随着间隙的增加，泄漏系数随之增加；间隙减小一半，泄漏系数约增加7%，泄漏流量增加近50%。而对于斜齿，其影响相对较小。黄守龙等[8]对3种不同深宽比的单空腔封严结构进行了数值模拟，表明存在一个合适的深宽比使得封严结构的泄漏流量最小。

以往针对蓖齿封严性能的研究主要通过实验测量、数值仿真、理论分析的手段来完成。随着计算流体力学的发展和完善，对于收缩-扩张型流道的模拟技术已较为成熟，计算的准确性也有较大保障。为此，本文通过数值模拟手段，全面研究不同压比下篦齿齿尖磨损、衬套磨损对篦齿封严性能的影响。

2 篦齿封严研究常用参数

篦齿封严研究常用参数有泄漏流量、流量系数、泄漏系数、雷诺数、泰勒数等。其中，流量系数定义为实际泄漏流量与理想泄漏流量之比[9]，即

式中：p0为进口总压，pn为出口静压，k为绝热指数，R为气体常数，A为间隙面积(A=πDc，D为间隙处对应封严结构直径，c为封严间隙值)。

3 计算模型

3.1 计算对象

以Denecke[10]的实验模型为研究对象，其几何模型如图1所示。图中Divergent表示上台阶流动，Convergent表示下台阶流动。其中，齿高为4.0 mm，齿宽为8.0 mm，齿尖厚度为0.4 mm，台阶齿间隙为1.3 mm，台阶高度为2.0 mm，齿数为4。

图1 台阶齿几何模型Fig.1 Geometric model of labyrinth seal step tooth

3.2 计算网格及边界条件

采用ANSYS ICEM 17.0软件生成结构网格。参考实验设备实际结构，图2示出了台阶齿计算域。采用ANSYS CFX 17.0计算，湍流模型选择k-ε模型。对于所有计算模型，y+max均在20以下，给定进口总压、总温，出口静压边界条件，通过改变进口总压改变其压比，静态计算时Wall 1～Wall 3均设置为绝热无滑移边界条件；两侧面设为周期性边界。

图2 台阶齿计算域Fig.2 The calculation domain of the step tooth

3.3 网格无关性验证

对于计算模型，其损失主要来源于齿尖处的节流效应、齿腔中的掺混损失及壁面的摩擦损失。为此，网格无关性验证过程中，主要加密齿尖、齿腔和壁面处网格，验证结果如图3所示。可见，网格数量为30万时，网格无关解已基本收敛。当压比为1.05时，Denecke通过实验得到其流量系数为0.297，本文仿真收敛结果为0.294，误差为0.89%，在可接受范围内。考虑计算的准确性与计算时间，后续的模拟中都使用30万网格规模。

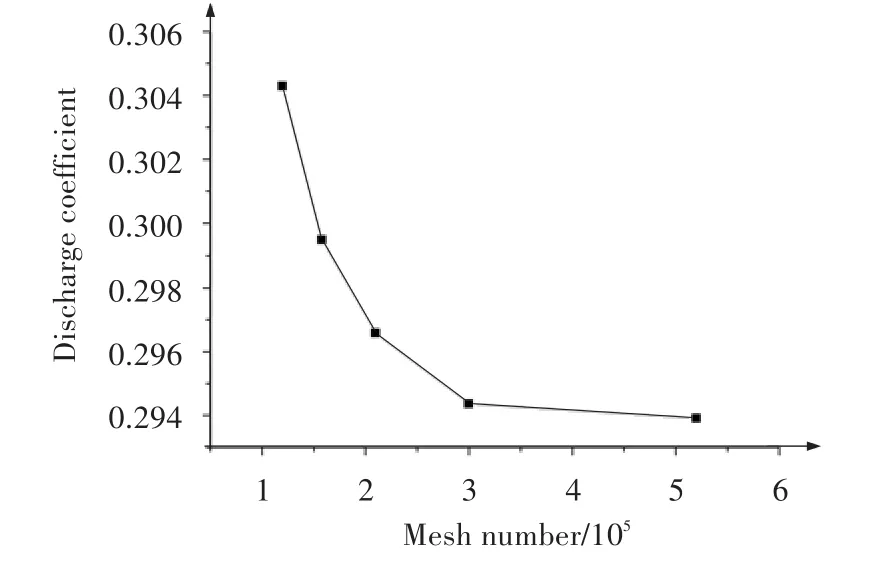
图3 网格无关性验证Fig.3 Validation of mesh sensitivity

4 计算结果及分析

4.1 压比对封严性能的影响

通过改变进口总压，计算不同压比下篦齿结构的流量系数。图4给出了上下台阶流动泄漏流量随压比的变化。由图可知，对于上下台阶流动，随着压比增加，其泄漏流量均随之增加，且上台阶流动的封严性能比下台阶流动的差。从具体的数值看，相同压比下，上台阶流动的泄漏流量比下台阶流动的增加了约16%。对于台阶齿，齿腔内部的掺混是决定其封严性能的一个主要因素，掺混越大其封严性能越好。图5给出了压比1.5时上下台阶流动的马赫数云图。可看出，此时在齿腔处，下台阶流动使得气流在齿腔中有了较长的流动路径，其透气效应较小，因此更多气流在齿腔中掺混并被减速，下台阶流动在齿腔中的损失显然高于上台阶流动的。

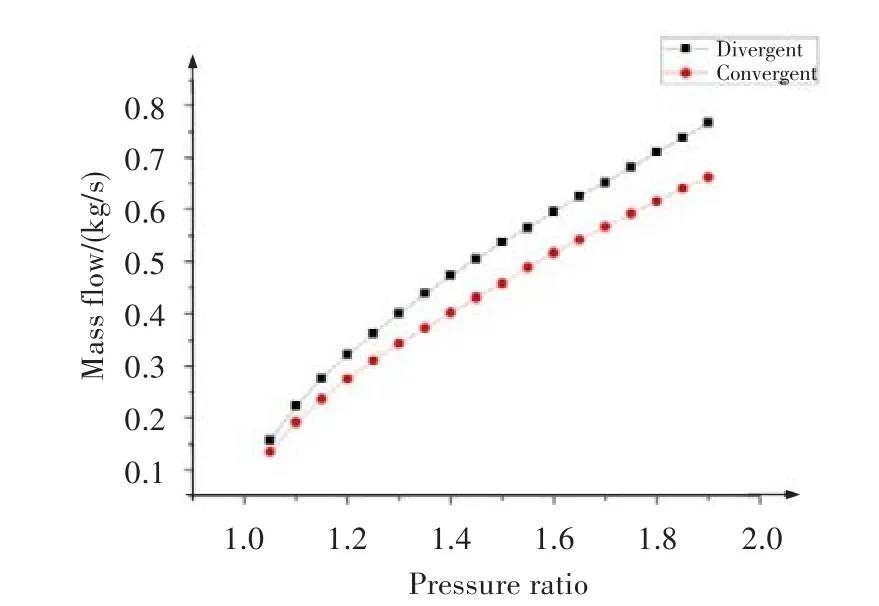
图4 上下台阶流动流量随压比的变化Fig.4 The change of the seal mass flow with pressure ratio

4.2 齿尖磨损对封严性能的影响

主要讨论齿尖前缘倒圆、尾缘倒圆、前缘尾缘倒圆三种情况下篦齿封严性能变化，倒圆半径(R)分别为0.1 mm、0.2 mm。图6给出了倒圆处网格细节。

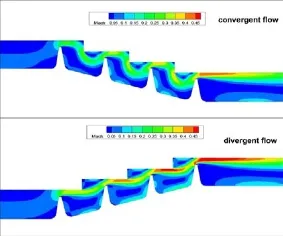
图5 压比1.5时上下台阶流动的马赫数云图Fig.5 The contour of Mach number in stepped flow(pressure ratio=1.5)

图6 前缘和尾缘倒圆处网格细节Fig.6 The meshes of leading and trailing edge of rounded section

图7 倒圆对上台阶流动流量的影响Fig.7 The change of divergent flow's mass flow in different rounded sections

图8 倒圆对下台阶流动流量的影响Fig.8 The change of convergent flow's mass flow in different rounded sections

不同倒圆情况下上下台阶流动流量随压比的变化，见图7、图8。图中，BE表示齿尖两侧均倒圆，LE表示齿尖前缘倒圆，TE表示齿尖尾缘倒圆。对于齿尖前缘倒圆，当R=0.1 mm时，不同压比下上、下台阶流动的泄漏流量相对齿尖未磨损时的，分别增加了约17.0%和14.5%，且随着倒圆半径的增加，封严性能进一步恶化；当R=0.2 mm时，上、下台阶流动的泄漏流量分别增加了约25.0%和23.5%。对于齿尖前缘尾缘均倒圆，当R=0.1 mm时，不同压比下上、下台阶流动的泄漏流量相对齿尖未磨损时的分别增加了约15.0%和13.5%，且随着倒圆半径的增加封严性能进一步恶化；当R=0.2 mm时，上、下台阶流动的泄漏流量分别增加了约26.0%和25.0%。对于齿尖尾缘倒圆，当R=0.1 mm时，不同压比下上、下台阶流动的泄漏流量相对齿尖未磨损时的分别下降了约0.9%和0.6%，且随着倒圆半径增加封严性能变好；当R=0.2 mm时，上、下台阶流动的泄漏流量分别下降了约2.3%和2.4%。可见，齿尖前缘和前缘尾缘倒圆将大大降低封严性能，齿尖尾缘倒圆对封严性能略有提升。相同条件下，对于上下台阶流动，倒圆对封严性能影响排序(封严性能逐渐变好)如下：0.2 mm的前缘尾缘倒圆、0.2 mm的前缘倒圆、0.1 mm的前缘倒圆、0.1 mm的前缘尾缘倒圆、未倒圆、0.1 mm的尾缘倒圆、0.2 mm的尾缘倒圆。

图9 前缘倒圆时不同倒圆半径的下台阶流动Fig.9 Convergent flow's streamline in leading edge rounded section

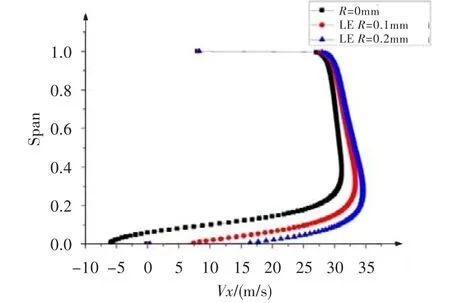
图10 前缘倒圆时下台阶流动齿尖中心截面的速度分布Fig.10 The convergent flow's velocity distribution at the center cross section of the first tooth tip in leading edge rounded section

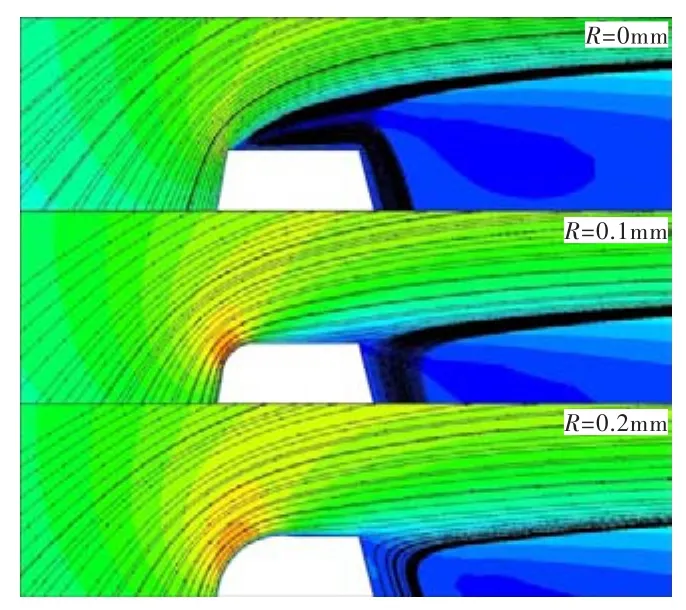
图11 前缘倒圆时不同倒圆半径的上台阶流动Fig.11 Divergent flow's streamline in leading edge rounded section

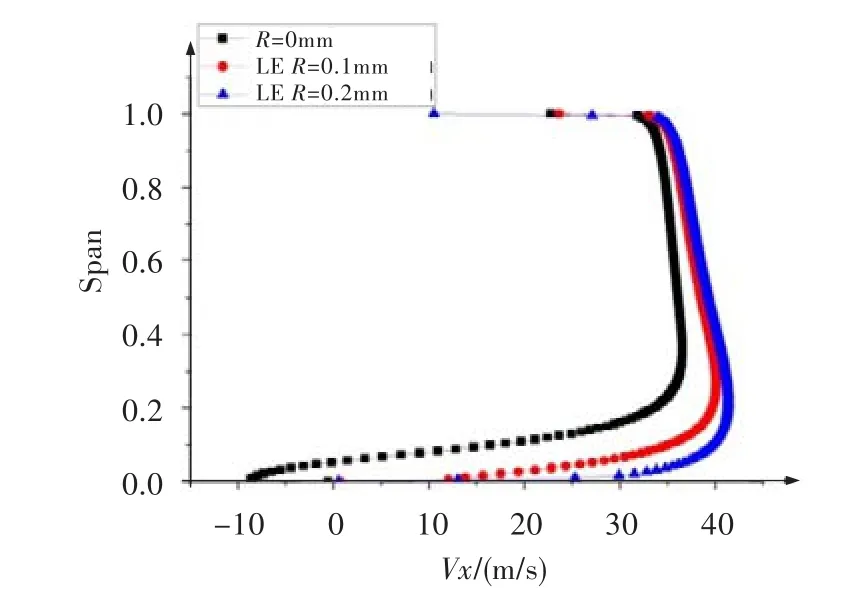
图12 前缘倒圆时上台阶流动齿尖中心截面的速度分布Fig.12 The divergent flow's velocity distribution at the center cross section of the first tooth tip in leading edge rounded section

图9～图12给出了前缘倒圆时不同倒圆半径的上下台阶流动流线及齿尖中心截面的速度分布。由图9、图11可看出，对于上下台阶流动，齿尖前缘倒圆使得齿尖处气流分离明显减小，且倒圆半径越大分离越小，进而导致齿尖处有效流通面积增加。由图10、图12可看出，齿尖前缘倒圆后齿尖前缘处气流的轴向速度均比未倒圆的大，特别是下壁面处；且因倒圆的存在，齿尖处的节流效应减弱、损失减少，因而沿流向气流流速增加。正是这两个原因的共同作用，导致齿尖前缘倒圆后其封严性能大大降低。

图13～图16为尾缘倒圆时不同倒圆半径的上下台阶流动流线以及齿尖中心截面的速度分布。由图13和图15可看出，对于上下台阶流动，尾缘倒圆使得齿尖有效流通面积略有减小。由图14和图16可知，尾缘倒圆后截面气流流动速度整体均比未倒圆时的小。这两个原因同时作用，导致泄漏流量有所减小。

图13 尾缘倒圆时不同倒圆半径的下台阶流动Fig.13 Convergent flow's streamline in trailing edge rounded section

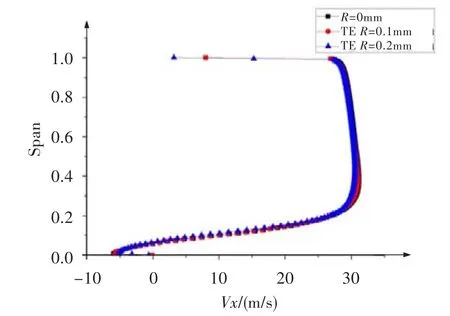
图14 尾缘倒圆时下台阶流动齿尖中心截面的速度分布Fig.14 The convergent flow's velocity distribution at the center cross section of the first tooth tip in trailing edge rounded section

图17～图20为前缘尾缘均倒圆时不同倒圆半径的上下台阶流动流线以及齿尖中心截面的速度分布。对比图9、图11可知，前缘尾缘倒圆与前缘倒圆的流动状态类似。由图17和图19可看出，当R=0.1 mm时，由于尾缘倒圆的作用仍在发挥，沿壁面处气流流速较小，因而相同情况下其封严性能比只在前缘倒圆的好；当R=0.2 mm时，由于气流流速较快，流过中心截面后突然扩张，使得气流有较大的速度贴着壁面流动。由图18和图20可看到，前缘尾缘倒圆后齿尖前缘处的轴向速度均比未倒圆的大，这是因为前缘尾缘倒圆后，齿尖处的节流效应减弱，损失减少，因而沿流向气流流速增加。

图15 尾缘倒圆时不同倒圆半径的上台阶流动Fig.15 Divergent flow's streamline in trailing edge rounded section

图16 尾缘倒圆时上台阶流动齿尖中心截面的速度分布Fig.16 The divergent flow's velocity distribution at the center cross section of the first tooth tip in trailing edge rounded section

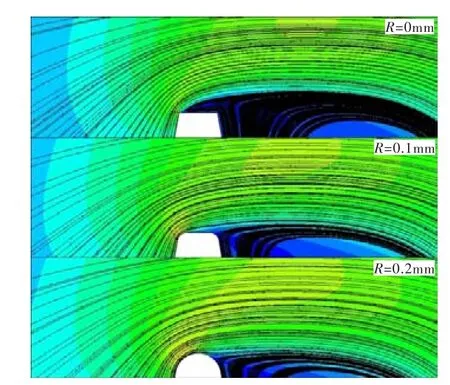
图17 前缘尾缘倒圆时不同倒圆半径的下台阶流动Fig.17 Convergent flow's streamline with different leading and trailing edge rounded section

4.3 衬套磨损对封严性能的影响

以光滑衬套为例，简化磨损模型，使磨损凹槽与台阶齿中心在同一竖直线上。为定性分析衬套磨损对封严性能影响，保证篦齿结构原间隙值不变，仅考虑衬套磨损的影响。分析了表1所示的6种模型。

图18 前缘尾缘倒圆时下台阶流动齿尖中心截面的速度分布Fig.18 The convergent flow's velocity distribution at the center cross section of the first tooth tip with different leading and trailing edge rounded section

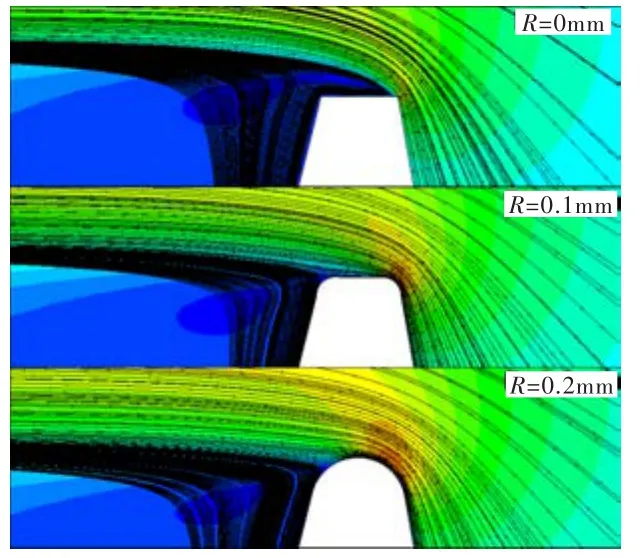
图19 前缘尾缘倒圆时不同倒圆半径的上台阶流动Fig.19 The divergent flow's streamline with different leading and trailing edge rounded section

图20 前缘尾缘倒圆时上台阶流动齿尖中心截面的速度分布Fig.20 The divergent flow's velocity distribution at the center cross section of the first tooth tip with different leading and trailing edge rounded section

图21、图22显示了衬套磨损对下台阶和上台阶流动泄漏流量的影响。结果表明：对于上下台阶流动，衬套磨损对封严性能有不利影响。随着磨损深度的增加，封严性能有所下降，但深度达到0.2 mm后泄漏流量趋于不变；随着磨损宽度的增加，泄漏流量也呈逐渐增加的趋势。

表1 6种分析模型Table 1 Six analysis model

图21 衬套磨损对下台阶流动封严性能的影响Fig.21 The convergent flow's performance change in the brushing worn condition

图22 衬套磨损对上台阶流动封严性能的影响Fig.22 The divergent flow's performance change in the brushing worn condition

对于上下台阶流动，表2给出了不同磨损深度下第一齿中心截面气流的平均速度。可看出，随着磨损深度的增加，其平均速度先减小后趋于不变。图23、图24为不同磨损深度的下台阶和上台阶流动的流线图。可看出，衬套磨损宽度不变时，随着磨损深度的增加，磨损处出现回流且回流区逐渐发展，当磨损深度为0.2 mm时回流区大小基本稳定。随着磨损深度的进一步增加，回流区大小几乎不变，因此磨损深度进一步增加对泄漏流量影响不大。

表2 不同磨损深度下第一齿中心截面气流的平均速度Table 2 The average velocity at the center cross section of the first tooth tip with different worn depth

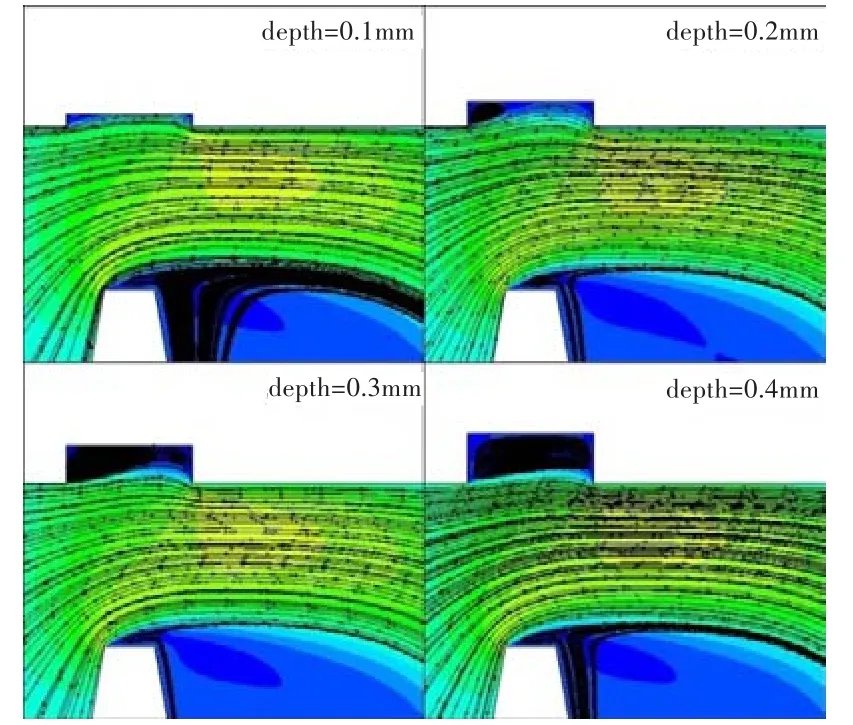
图23 不同磨损深度的下台阶流动Fig.23 The convergent flow with different worn depth

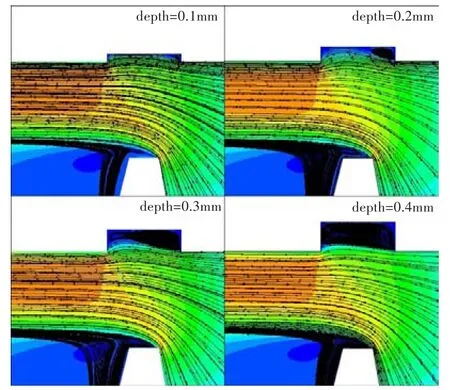
图24 不同磨损深度的上台阶流动Fig.24 The divergent flow with different worn depth

对于上下台阶流动，表3给出了不同磨损宽度下第一齿中心截面气流的平均速度。由表可知，随着磨损宽度的增加，齿尖中心截面处的平均速度略有增加。图25～图28为不同磨损宽度的上下台阶流动流线及第一齿尖中心截面的速度分布(图26和图28中，纵坐标表示从齿尖中心点处到磨损底部中心点处的无量纲长度)。由图25和图27可看出，衬套磨损深度不变时，随着磨损宽度的增加，磨损处涡系结构逐渐减小，气流有效流通面积有所增加。由图26和图28可看出，在齿尖的近壁面处流动速度型基本一致。在0.2～0.4和0.8～1.0的无量纲长度处，1.2 mm磨损宽度下的速度比其他两种小磨损宽度的大，0.4～0.8无量纲长度处则相反。综上分析可知，封严泄漏流量随着磨损宽度的增加而增加。

表3 不同磨损宽度下第一齿中心截面的气流平均速度Table 3 The average velocity at the center cross section of the first tooth tip with different worn width

图25 不同磨损宽度的下台阶流动Fig.25 The convergent flow with different worn width

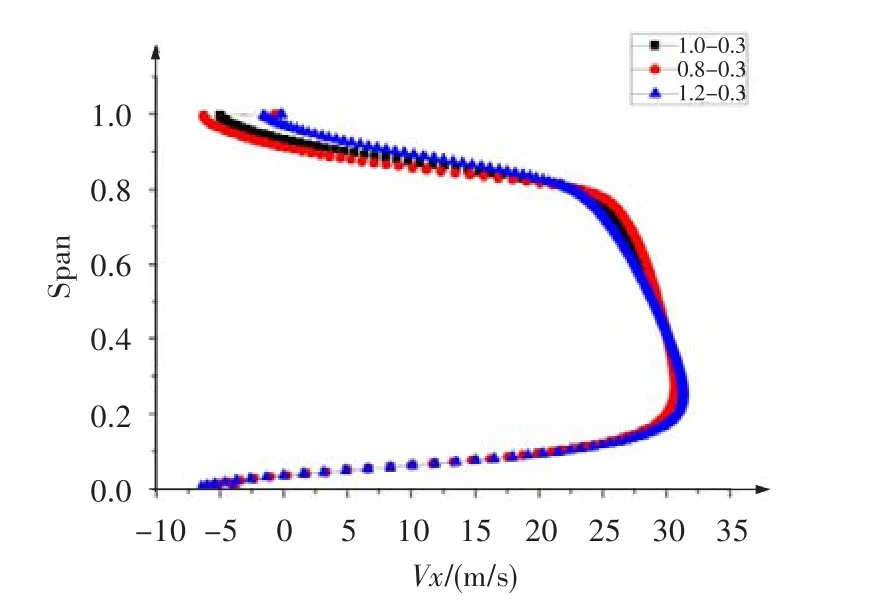
图26 不同磨损宽度的下台阶流动第一齿尖中心截面的速度分布Fig.26 The convergent flow's velocity distribution at the center cross section of the first tooth tip with different worn width

图27 不同磨损宽度的上台阶流动Fig.27 The divergent flow with different worn width

图28 不同磨损宽度的上台阶流动第一齿尖中心截面的速度分布Fig.28 The divergent flow's velocity distribution at the center cross section of the first tooth tip with different worn width

5 结论

(1)齿尖前缘磨损和齿尖前缘尾缘磨损对封严性能有不利影响，齿尖尾缘磨损对封严性能有一定提升作用。在所模拟的最恶劣情况(齿尖前缘尾缘均被磨损，磨损半径为0.2 mm)下，会导致泄漏流量增加约26.0%。

(2)衬套磨损对封严性能有不利影响。随着衬套磨损深度的增加，其封严性能逐渐下降，到一定深度(0.2 mm)后性能恶化趋于不变。衬套磨损宽度对封严性能的影响相对较大，随着磨损宽度的增加，会造成封严性能持续下降。文中探讨的最大磨损宽度为齿尖宽度的3倍，此时其泄漏流量增加了约6%。