浅海小掠射角的海底界面声反向散射模型的简化*

2019-03-16侯倩男吴金荣

物理学报 2019年4期

侯倩男吴金荣

(中国科学院声学研究所,水声环境特性重点实验室,北京 100190)

在浅海,尤其是负梯度声速剖面和海面较为平静的浅海波导,海底界面反向散射是浅海混响的主要来源.经验散射模型只适用于分析浅海混响平均强度衰减特性,而基于物理机理建立的反向散射模型克服了这一缺陷,但同时也引入了其受地声模型约束的问题.本文结合了海底反射系数的三参数模型,对浅海远场海底反向散射模型进行了简化,以减少地声模型的输入参数.理论分析了海底反射系数的相移参数可以描述海底对声场的散射作用,无需任何海底地声参数的先验知识.通过对海底反向散射模型近似简化,结果表明在临界角附近和甚小掠射角范围内的海底粗糙界面反向散射模型的角度特性和强度特性受海底沉积层的影响不同:在临界角附近,海底反向散射的角度特性受海底反射系数的相移参数加权,而其散射系数则近似与相移参数无关;对于甚小掠射角,海底反向散射的角度特性近似与海底反射系数的相移参数无关,其散射系数则近似与相移参数的4次方成正比.

1 引言

海底作为浅海混响的主要散射源,浅海海底界面混响是很多学者探究的课题.浅海混响根据其形成过程可以分为传播和散射两个过程.入射声传播和散射声传播过程同属信道声传播问题,研究较为完善.而散射过程则比较复杂,散射强度的测量也较难实现,尤其是小掠射角的反向散射的测量,所以针对散射的研究相对比较受限.在混响研究伊始,各国学者均采用经验的散射模型描述海底对声场的散射作用.由于其形式较为简单,运算速度较快,在主动声纳预报系统中有很大的优势[1−4],至今仍被延续使用.但是该类型的散射模型也存在着很大的局限性,很难分析海底散射机理.最初的经验散射模型是借鉴光学理论中提出的半无限自由空间中的Lambert散射定律给出的海底散射模型,是海底散射强度与平面波掠射角之间的关系.而在波导环境中,由于频散效应的存在,平面波散射理论不再适用于声场处理,遂采用简正波理论,避免了频散产生的多途现象.然而简正模态的掠射角不同于平面波的掠射角,因此对波导环境中的声散射问题不能够直接采用经验的Lambert散射模型.近年来,越来越多的学者开始从海底散射的物理机理着手建立散射模型.国际上关于物理散射模型的建模方法包括有限元方法[5]、Kirchhoff近似方法[6]、微扰近似方法[7−10].国内关于物理散射模型的研究最具代表性的是中国科学院声学研究所的高天赋和尚尔昌.Shang等[11]在Gao[12]和Tang[13]的研究基础上提出了全波动混响理论,并对该模型进行了一系列的发展.2001 年,Gao 等[14]提出了依据混响数据反演海底反向散射矩阵的方法.Wu等[15,16]将海底反射模型引入到浅海混响模型中简化了混响衰减特性与海底沉积层参数之间的关系,为海底地声参数的反演提供了一种新方法.

本文在尚尔昌和吴金荣的研究基础上,对反向散射模型进行进一步分析.通过引入海底反射系数的相移参数,描述海底对声场的散射作用,分析海底反向散射模型的角度特性和强度特性.在实际应用允许的误差范围内,进一步分析海底粗糙界面反向散射模型的角度特性和强度特性,并与经验散射模型进行对比,说明两者之间的异同.

2 浅海全波动混响理论

在浅海波导环境中,海底粗糙界面是海底混响的主要散射源.在图1所示的浅海波导环境中,平坦海底的平均海深为,任意水平位置的海底粗糙界面相对于平均海深的起伏高度为,其量值远小于,均值为 0,方差为.海底粗糙界面对声场的散射强度远小于入射声场的强度,即满足弱散射的条件.海底为半无限均匀介质,其声速、密度和声吸收系数分别为(声吸收系数的单位是).海面为平坦的自由边界,不考虑其对声场的散射作用.

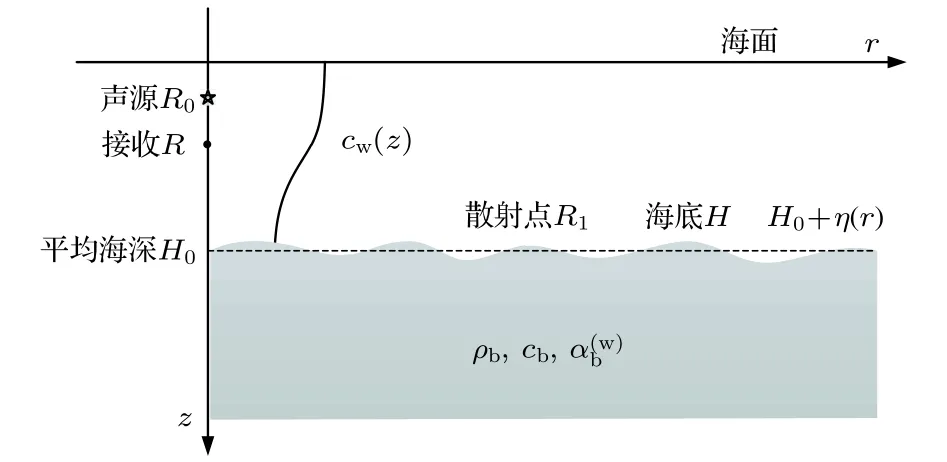
图1 浅海波导环境Fig.1.Shallow water waveguide environment.

2.1 浅海海底粗糙界面散射

全波动混响理论的基础思想是将海底粗糙界面对声场的散射作用看作是“二次声源”向外辐射声能量,从而将海底粗糙界面的散射作为“声源”向波导环境中辐射声能量[11].该“声源”的声源强度与入射声强度成正比关系.在水平均匀的波导环境中,单位简谐点源入射声场满足波动方程为

海底粗糙界面的“二次声源”满足

根据格林定理,水平均匀波导环境中,“二次速度源”在接收点处的辐射声场可以通过格林函数给出形式解.辐射声场的格林函数满足

同时满足边界条件

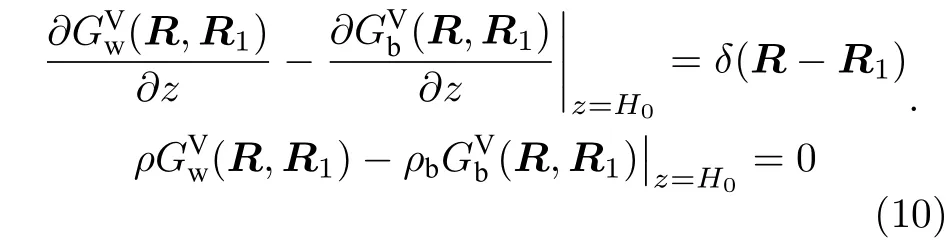
在接收点“二次速度源”的辐射声场满足形式解,

对于本地混响,声源和接收均在同一水平位置.为了方便计算,通常令其位于过源点的垂直轴线上,即.将 (4）—(6）式代入 (17）式,并通过分部积分法得到简谐点源的海底粗糙界面的反向散射声场,将其描述为简正模态的叠加形式[11],

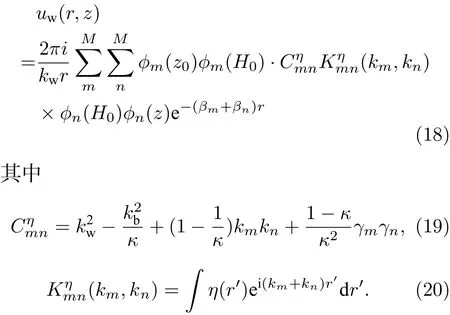
2.2 浅海海底粗糙界面混响

实际上(18）式是平坦波导环境中海底粗糙界面散射场的稳定解形式.对于声源脉冲信号s(t),其功率谱满足Fourie变换

其中,t0是信号的传播时间,与散射环的水平距离满足.

混响是能够同一时刻被接收、来自各方向散射回波的叠加.对于海底粗糙界面混响而言,同一时刻接收到的散射回波来自于宽度为的.对(23）式计算强度,并在散射环面积上进行积分得到海底粗糙界面混响平均强度

在这里,只考虑其非相干特性,得到短脉冲的非相干混响平均强度

是区别于经验散射模型的物理散射模型.它结合了波导环境特性和简正波理论的思想,建立了受格林函数约束的散射模型,明确了海底地声参数以及海底粗糙界面与海底反向散射的定量关系.因此,地声参数的准确度直接影响到海底反向散射函数的精确度.通常情况下,很难直接获取大面积的地声数据,通过反演得到的地声参数又受地声模型的影响较大,而且反演的未知参数较多,导致结果存在很大的不确定性.从反射系数的角度思考,海底对声场的影响主要体现在海底反射系数.海底反射系数的三参数模型与海底地声模型无关,且参数较少,利用海底反射系数代替地声参数作为输入参数,能很大程度上简化海底粗糙界面的反向散射模型.

3 海底反射系数的三参数模型

尚尔昌在1979年提出了海底反射系数的三参数模型[17],随后给出了海底小掠射角的反射系数幅值和相移与掠射角之间的量化关系,该参数与地声模型无关.海底反射系数的幅值用Q参数表示

(33）式和(34）式分别给出了不同海底掠射角时海底反射系数的相移参数的不同形式.是甚小掠射角处的海底反射系数相移参数,是海底沉积层和水介质的声速比和密度比的函数;是临界角附近海底反射系数的相移参数,是临界角的函数.

海底反射系数的幅值参数Q与地声参数之间的转换关系满足[18,19]

联合(37）式和(33）式得到甚小掠射角的海底反射系数的相移参数与密度之间满足关系式

(37）式和(38）式分别是海底反射系数的参数与等效的均匀半无限海底介质的地声参数之间的转换关系.

4 海底粗糙界面反向散射模型

常用的经验散射模型如(39）式所示:

(30)式的海底反向散射模型是根据波导环境建立的散射模型,明确了入射简正模态、散射简正模态以及海底地声参数对反向散射的强度特性和角度特性的影响.浅海波导环境中简正模态是受格林函数严格约束的稳定解,与海底沉积层的介质参数和水文环境有关.在掠射角小于临界角的条件下,忽略各阶简正模态的水平波数(掠射角)之间的差异,即,则 (19）式可以近似描述为与模态无关的量.

将(37）式和(38）式代入(40)式,用海底反射系数的相移参数代替地声参数,得到

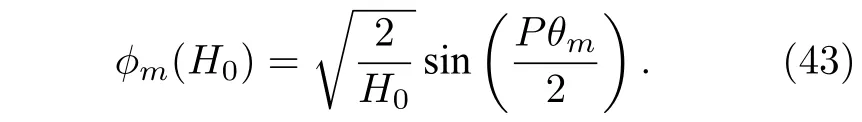
将(41）式和(43）式代入(30)式得到远距离(小掠射角)条件下的海底反向散射核函数,

4.1 角度特性

在远距离条件下,(44）式表明,海底反向散射的角度特性受海底反射系数的相移参数的影响,不同于经验散射模型.在临界角附近,

4.2 强度特性

通过4.1节的分析,掠射角不同时,海底反向散射的角度特性不同,同时也反映了海底反向散射系数的差异.

(47）式指出,在临界角附近,海底反向散射系数由海底反射系数的相移参数P、海底界面粗糙度谱,海深以及声源信号的频率决定.忽略临界角附近以及甚小掠射角的P参数之间的差异[18],则(42）式中等式右边第三项相比前两项为小量,可以忽略不计.第二项中采用小角度近似,

图2 随 P 参数的变化Fig.2. varied with P parameters near critical angle.

图3以第一类海底为例说明了这种近似结果的合理性.图中给出了甚小掠射角的海底反向散射系数随参数的变化曲线(仿真参数:海深为50m,声源频率为600Hz,海底粗糙界面的标准差为,相关尺度为,计算得到Goff-Jordan谱[20]为－32.8dB)以及对其进行参数的四次方拟合结果,两者的变化趋势基本一致.所以,在甚小掠射角的条件下,海底反向散射系数与海底反射系数的相移参数密切相关,即与海底沉积层的声速比和密度比有关,与声吸收系数无关.

图3 海底甚小掠射角反向散射系数对P参数的依赖Fig.3.Relationship between P and bottom backscattering coefficient at very low grazing angle.

另外,从混响平均强度的角度分析,同样说明了这种近似的合理性.海底界面粗糙度谱函数采用图3的仿真参数,海底是第一类均匀半无限介质,声速为,密度为,声吸收系数为,海深为 50m,水介质为 1500m/s的等声速剖面的均匀水体.声源频率为600Hz,发射深度为 10m,接收深度为 30m.计算水平散射距离从5km到50km的混响平均强度衰减曲线.图4中实线是根据(30)式仿真的非近似混响平均强度衰减曲线;“○”是根据(46）式和(53）式仿真的临界角的近似结果,与非近似的混响平均强度衰减曲线在13km以前完全重合;随着水平距离的增加,两者相差逐渐增大;“”是根据 (49）式和(54）式仿真的甚小掠射角的近似结果,在20km以前,与非近似结果之间的差异随水平距离的增大而减小,在20km以后两者基本吻合.在散射距离较近时,掠射角相对较大,临界角附近近似的海底反向散射模型与真实结果更接近;在散射距离较远时,掠射角相对较小,甚小掠射角的近似结果与真实结果更接近.

图4 海底反向散射模型的比较Fig.4.Compare with bottom backscattering model with different approximate.

5 结论

在浅海混响平均强度模型中,经验散射模型在混响特性分析中存在明显的局限性,而现有的物理散射模型受地声模型的影响较大.本文以全波动混响理论的物理散射模型为基础,结合海底反射系数的三参数模型,将海底反射系数的相移参数等效代替地声参数,描述海底对声场的散射作用,简化了海底反向散射模型.通过理论分析,明确了海底掠射角以为分界点,海底反向散射的角度特性和强度特性对海底反射系数的相移参数存在不同的依赖关系.在掠射角满足时,海底反向散射的角度特性近似描述为与可分离经验散射模型的角度特性一致,与参数无关;而其散射系数则近似描述为与P4线性增强.当海底掠射角满足,海底反向散射的角度特性是受参数加权的,即受海底地声参数的影响;而其散射系数则近似为与参数无关.所以不同掠射角范围,海底对反向散射声场的强度特性和角度特性的贡献不同.掠射角较大时海底对反向散射声场的影响主要体现在其角度特性;掠射角非常小时,海底的影响主要体现在其强度特性.

附录A 经验反向散射模型

经验反向散射模型有多种形式,主要体现在其角度特性之间的差异.最常用的海底散射模型是可分离的散射模型,