一种工程化的海洋混响仿真模型研究

郭燕子 李国良 张福生

（91388部队 湛江 524022）

1 引言

随着现代仿真技术的发展，对自导鱼雷在水声对抗环境下攻击目标的全弹道仿真的研究也越来越深入，鱼雷的仿真主要是针对鱼雷的制导系统进行仿真，其中鱼雷自导的仿真是鱼雷制导系统仿真中的一个重要内容，其内容包括基阵的波束形成仿真、噪声干扰仿真、混响干扰仿真、信号检测与参数估计、目标识别的仿真等内容。海洋混响是海洋环境产生的回声，对于鱼雷制导来说，混响是一种严重的干扰［1］，研究海洋混响仿真模型，对于研究现代鱼雷的仿真具有重要的意义。

2 海洋混响的离散统计模型

对于主动声自导鱼雷的信号检测处理而言，其干扰主要有噪声干扰（包括鱼雷自噪声、海洋环境噪声等综合噪声）和海洋混响干扰，其中噪声干扰伴随鱼雷自导工作的整个过程，而混响干扰则由于与鱼雷自导发射的信号能量、信号体制密切相关，其对鱼雷的自导干扰表现为鱼雷的信号从发射结束转为接收后的一小段时间内，但对自导的干扰是相当厉害的。混响的产生是由于发射信号在海洋信道传播过程中被水介质中各种不均匀颗粒和界面（包括海面和海底）的不平整散射所引起。混响和发射信号有着直接的关系，直观上可理解为它和发射信号存在着某种内在的联系，但由于海洋环境的复杂性，很难建立混响和发射信号之间的确定关系，但在一定的假设前提下，建立发射信号和混响之间的统计关系是可能的［2-5］。

把混响模型看作是一个时间随机过程F(t)，并作如下假设：

1）海洋中各颗粒杂质散射的不均匀性是离散的；

2）不存在二次散射，且认为介质是均匀的。

在以上的假设前题下，混响的时间随机过程F(t)可表达为

式（1）中，N是在t时刻接收点上产生混响元散射信号的个数，fk(t)是第k个元散射信号所形成的一个函数，它可表达为

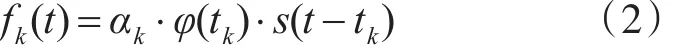
式（2）中，αk表示第k个元散射体的散射性质的随机变量，φ(tk)表示信号在水介质中传播时衰减情况的一个函数，tk表示第k个元散射信号到达接收点的时间，s(t)为自导鱼雷的发射信号。

F(t)可以写成如下形式：

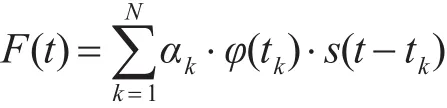
假设发射信号 s(t)=A(t)⋅cos[ϖ0t+φ(t)]，则

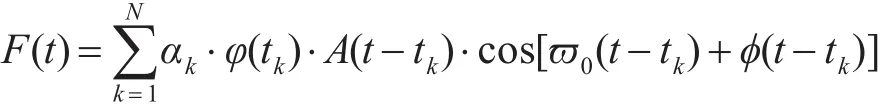
F(t)的解析函数Y(t)为

又s(t)的复包络可表示为

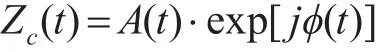
则混响的复包络YF(t)

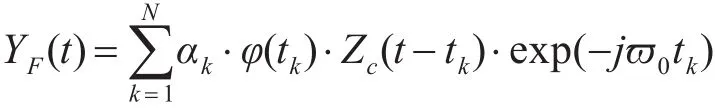
令

在上式混响的复包络模型中，有关随机参量的概率分布情况，我们假定在水介质中散射体是独立分布的，并且从散射性质的观点来看彼此不影响，认为这些随机参量是统计独立的。

3 海洋混响的仿真模型

海洋混响是由于海水介质及海面和海底对自导鱼雷的声探测系统发射信号产生的声散射在接收点叠加而成的结果，是限制主动自导鱼雷对近距离目标检测的主要因素，理论研究表明，与海洋噪声相比，混响有其自身的特点［6～10］，主要表现为

1）混响强度与发射信号的能量有关，两者是正比关系；

2）混响与发射信号相关，并且混响本身具有一定的相关性；

3）混响振幅呈瑞利分布；

4）混响频谱相对于发射信号有频谱扩展；

5）混响是时空变化的，其强度随时间增加而逐渐衰减，并且在不同的海域、不同的季节甚至中午和下午都各不相同。

准确地仿真海洋混响是不现实的，在工程中只能采用简化的方法，利用以上建立的混响离散统计模型，把混响看成一个可平稳化的高斯随机时变过程，混响的包络服从瑞利分布，混响强度的衰减规律近似用指数衰减规律拟合。

海洋混响的生成方法可用图1表示。

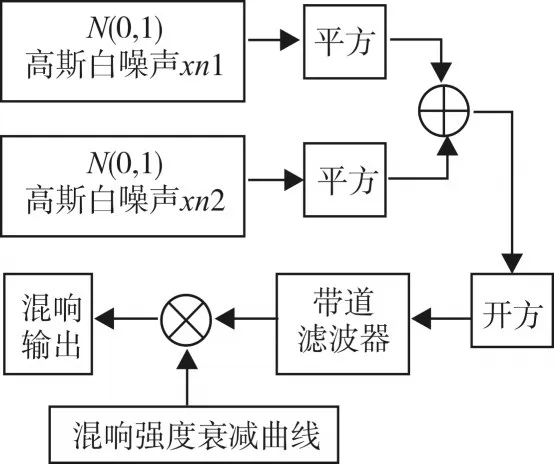
图1 海洋混响干扰的生成框图

3.1 混响带通滤波器的设计［11］

要设计带通滤波器，首先要确定滤波器的带宽，前面已经分析，混响的带宽与发射信号密切相关，但要比发射信号的带宽宽一些，称之为频率扩展；频率扩展一方面与海洋中散射体的多普勒和随机相移有关，另一方面与发射信号包络的时间长度和形状有关，还与自导系统波束宽度有关。

若发射信号是单频CW矩形脉冲，则混响带宽近似为

若发射信号是线性调频矩形脉冲，则混响带宽近似为

其中，BW 混响带宽的单位是赫兹（Hz）；T是发射信号的脉冲宽度，单位是秒（s）；WLFM是线性调频信号的调频宽度，单位是赫兹（Hz）。

从式（4）我们看出，若发射信号的脉冲宽度T为40ms，则可以算出BW 为50Hz，若系统中心频率为30KHz，系统采样率为90KHz，50Hz的带宽与之相比就显得太小，归一化的带宽只有九百分之一，这对滤波器设计带来很大的困难。

通过对几种滤波器的分析比较，采用椭圆形滤波器，利用椭圆函数设计的椭圆滤波器，它的误差在通带和阻带内都是按等波纹形式分布的。实现相同的滤波器设计指标时，椭圆滤波器的阶数最低。在相同的阶数条件下，则椭圆滤波器的性能指标最高。

在具体混响仿真中的具体做法是借用Matlab中有关椭圆滤波器设计的几个函数，将它们转化成标准C语言的子程序，然后在Visual C++中调用［11］。转换工具是一个叫做MATCOM的实用程序。

［n Wn］=ellipord（Wp/（fs/2），Ws/（fs/2），rp，rs，z）；

［b a］=ellip（n，rp，rs，Wn，‘bandpass’）

filter（b，a，xn）；

采用上述椭圆滤波器处理的效果非常好，在采样率为300KHz的情况下，可以滤出通带带宽为30Hz的混响，滤波器的归一化带宽只有5000分之一，并且可以做到通带内衰减在3dB之内，阻带内衰减在30dB以上。

3.2 混响包络曲线的确定

用以下指数衰减曲线拟合混响的包络曲线：

假定自导鱼雷的发射脉冲周期为2s，再假定自导系统接收回波1.2s后，混响干扰衰减接近为零，则取α≥2.85可满足要求，我们取α=2.85；而A则主要用于控制幅度，可以根据每型鱼雷的发射声源级的不同加以确定。

4 海洋混响的仿真结果

利用以上建立的模型对混响进行仿真，取CW和LFM信号的中心频率 f0=22kHz,脉冲宽度T=40ms，LFM信号的调频宽度WLFM=1kHz的模拟结果。

比较图2和图3可以看出，混响仿真信号在频率上并不和发射信号完全相吻合，而是在频谱的两侧都有频移，形成一定的频带扩展。

图2 LFM脉冲混响信号及其频谱图

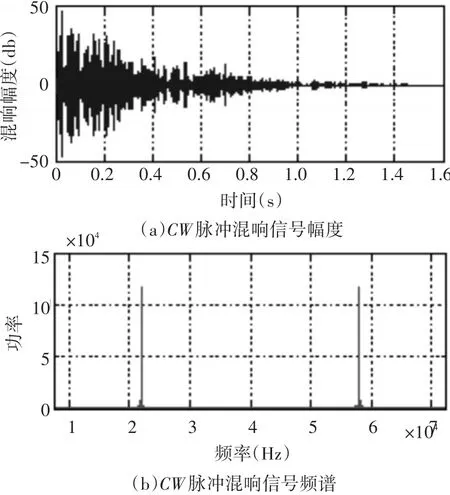
图3 CW脉冲混响信号及其频谱图

5 结语

本文提出并建立混响干扰模型已成功运用于某水声对抗试验仿真系统，实践表明，该模型可以满足鱼雷自导系统仿真中对混响干扰模拟的要求。