一维准周期晶格的性质及应用*

王玉成 刘雄军 陈澍

1）(南方科技大学物理系,深圳量子科学与工程研究院,深圳 518055）

2）(北京大学物理学院,国际量子材料中心,北京 100871）

3）(中国科学技术大学,量子信息与量子物理协同创新中心,合肥 230026）

4）(中国科学院物理研究所,北京凝聚态物理国家研究中心,北京 100190)

5）(中国科学院大学物理科学学院,北京 100049）

6）(量子物质科学协同创新中心,北京 100084）

准周期晶格在冷原子领域被广泛研究,它使得人们可以在一维或者二维系统里研究扩展到安德森局域的转变.2008年,Inguscio研究组在冷原子系统里制备了一维准周期晶格,并观测到了安德森局域化现象,这极大地推动了准周期系统的理论和实验研究.后来,Bloch研究组在制备的一维和二维准周期晶格中都观测到了多体局域的现象.最近,他们还在准周期晶格中成功观测到迁移率边以及存在迁移率边的系统的多体局域现象.这些冷原子实验推动了多体局域以及迁移率边等方向的研究.准周期晶格已经成为一个平台,它对很多物理现象的影响正在被广泛研究,并可以尝试在冷原子实验中观测到这种影响.本文结合作者的一些相关工作,对一维准周期晶格一些近期的研究进行了简要综述,介绍了一些相关的重要的冷原子实验,讨论了准周期晶格的一些重要性质,以及它对一些物理现象(比如拓扑态)的影响.

1 引 言

近三十年来,随着一系列原子的激光冷却与陷俘技术的实现和进步[1],人们能够研究超冷原子气体中新奇的量子现象.一些关键性的技术,比如菲斯巴赫(Feshbach)共振技术[2],应用到冷原子系统上,人们可以调节原子间的有效相互作用.由于超冷原子气具有高度纯净和容易操控的优点,成为了理想的量子模拟的平台,比如人们已经成功模拟了费米和玻色哈伯德(Hubbard)模型[3],自旋轨道耦合[4,5],拓扑模型及相变[6,7],科斯特利茨-索利斯(Kosterlize-Thouless)相变[8],甚至霍金辐射[9]等.所以现在的理论物理学家提出一个新的现象时,往往会考虑怎么在冷原子中模拟这种现象.另外,这些量子模拟不仅仅是验证凝聚态里的一些已知的结果,而且通过引入一些参数和新的环境,可以得到一些新的物理现象,这些新的物理现象又推动了理论物理的发展.

在 1980 年,Aubry 和 André研究了一维准周期系统[10](以下简称AA模型).尽管该系统不是随机无序的,但是它仍然没有平移对称性,它具有扩展到局域的转变的性质.此后,对于该模型以及该模型的一些推广[11−14]被广泛研究.2008 年,Roati等[15]在冷原子系统里成功模拟了AA模型,并且观测到了安德森局域化的现象.这开启了人们在冷原子系统里研究局域化问题的新篇章,一系列理论与实验的成果被发现.同时AA模型成为了研究其他物理现象的重要平台,比如在AA模型上加上p波配对项[16−19],可以用来研究拓扑超导到安德森局域相的转变,在AA模型上加上相互作用[20−22],可以研究热化相到多体局域相的转变.2015年,Schreiber等[23]在冷原子里制备出了带有相互作用的AA模型,从而第一次观测到多体局域相,这在一定程度上引发了多体局域研究的热潮.

本文详细介绍一些一维准周期系统及其应用,先介绍AA模型以及它的实验实现和在其基础上的一些推广模型,接着在AA模型上加上相互作用,讨论热化到多体局域的转变,并介绍如何在冷原子实验中观测多体局域现象,然后介绍AA模型相关的动力学研究,最后讨论准周期势对拓扑超导和拓扑半金属的影响.

2 AA模型简介及其冷原子实验实现

2.1 AA模型简介

1958年,美国物理学家Anderson[24]研究了无序晶体中电子的运动,提出了强无序体系中电子局域化的概念.由于无序的存在,晶格的周期性被破坏,电子的波函数不再能扩展到整个晶体中,而是在空间中按照指数形式衰减,这就是局域态.由于无序的存在,动量不再是描述电子态的好量子数,因此通常采用紧束缚近似,在瓦尼尔基下进行讨论.考虑安德森模型其中表示第 i个格点的态矢量,表示格点之间的跃迁,是 i 格点的化学势,它在范围内随机分布.本征态可写为中是粒子在 i 格点的概率幅.容易得到动力学方程为

对于一维或二维系统,很弱的随机无序就会使系统变得局域.AA模型是一个一维准周期系统[10](也可以称为非公约系统),其哈密顿量为

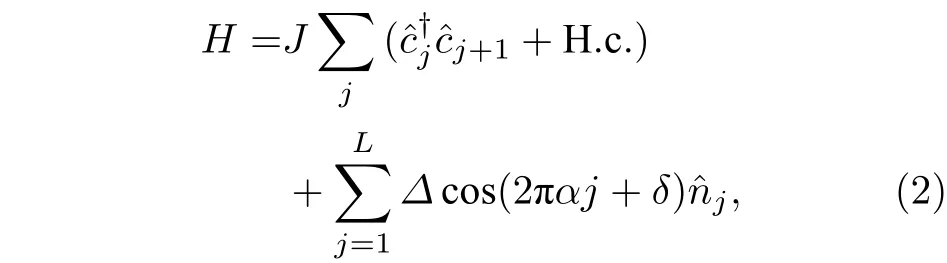
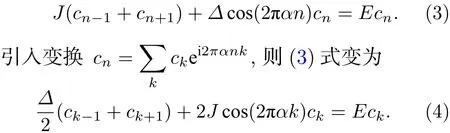
可以看到(3）式和(4）式有着完全类似的形式,这时称这两个方程是对偶的.对于固定的和,如果波函数∑ 是扩展的(局域的),其变 到对偶空间的波函 数∑ 应该是局域的 (扩展的).所以这个系统的扩展-局域的转变点是.

为了直观展示AA模型的扩展局域的性质,下面研究这个系统的倒参与率(the inverse participation ratio,IPR)和波函数的分布.倒参与率是一个最常用的描述系统局域扩展性质的量[25–27]:系统的第个本征态,它满足归一化条件1.如果一个态是扩展的,容易验证,当时,趋于 0.而对于局域态,在热力学极限下,IPR是一个有限的非零值.固定跃迁强度和系统尺寸,在图1中展示了AA模型的基态的倒参与率随准周期势强度的变化,这里取的是开边界条件(open boundary condition,OBC).可以看出,IPR 在时接近于零,在处突变为一个有限值,说明系统在这一点从扩展态变为了局域态.在图1的左右插图中,分别展示了和时系统的基态波函数的分布,可以看出时系统的基态波函数分布在整个空间,这是扩展态的特征,而时系统的基态波函数分布在一个很小的区域内,这是局域态的分布特征.不止是基态,容易验证其他态仍然有类似的特征.

图1 基 态 的 倒 参 与 率 随 的 变 化 ， 这 里 固 定 和.左 右 的 插 图 分 别 展 示 了 和 时系统的基态波函数的分布Fig.1.IPR of ground states as a function of for this system with and .The left and right insets show the distribution of the ground state withand respectively.

2.2 AA模型的冷原子实验实现

由于晶体中存在电子-电子以及电子-声子的相互作用,所以很难在晶体中直接观测到安德森局域化.冷原子系统干净和可控的特性为直接观测到安德森局域现象提供了可能.2008 年,Roati等[15]在冷原子系统中成功模拟了AA模型,并在此基础上观测到了安德森局域态.他们首先在光势阱中冷却得到一团玻色-爱因斯坦凝聚体(Bose-Einstein condensate),然后通过菲斯巴赫共振技术将原子间的相互作用调到零,最后将其放入一维双色光晶格中,如图2所示[15].一维双色光晶格势可以通过两束激光以驻波的形式产生,一束激光的波长为,产生主晶格,另一束波长为产生弱的次晶它们的形式为[28,29]:

式中矩阵元为

图2 实验实现准周期晶格的原理示意图.J描述的是主晶格最近邻格点之间的跃迁, 是由次晶格导致的在位能最大的差别Fig.2.Sketch of the quasiperiodic lattice realized in the experiment.J describes the hopping between the nearestneighbor sites of the primary lattice and is the maximum shift of the on-site energy induced by the secondary lattice.

考虑到晶格势很深时瓦尼尔函数的高度局域化,这里交叠积分只取到了跃迁项的次近邻部分和次晶格势的在位部分.利用和

(9）式最后一项的积分可以写成AA模型中的准周期势项对应的形式.定义

舍去常数项,易得

因此,得到了AA模型类似的哈密顿量

实验上可以测量系统的输运性质来研究扩展-局域转变:突然撤掉简谐势让原子在这个晶格中运动,然后利用原位吸收成像技术测量原子随时间的演化.会发现在准周期势强度很弱的情况下,系统迅速膨胀;而在准周期势强度很大的情况下,系统基本上没有扩散发生.这和前面通过动力学方程对安德森模型中扩展态和局域态的描述是一致的.

3 AA 模型的推广

3.1 存在迁移率边的一维准周期模型

对于三维系统,如果加的无序强度在某个范围内,系统的能带中可能会出现迁移率边和.满足的本征值对应的态是扩展的,如果费米面在这个范围内,系统就表现出金属属性,或者范围的本征值对应的态是局域的,如果费米面在这个范围,系统就表现出绝缘体属性.通常可以通过掺杂、加压或者加电磁场等方式调节费米面或迁移率边的位置,从而使系统可以发生金属-绝缘体的转变.

在AA模型之后,科学家们在此基础上提出几个准周期模型[11−14],这使得可以在一维系统里研究迁移率边.如哈密顿量(2）式中化学势项写为.可以看出,当时,该系统简化为AA模型.固定跃迁强度,理论和数值研究发现,当以及时,这个系统存在迁移率边,在能带的中间(),所有的态是扩展的,在能带的两边(),所有的态是局域的,是两个迁移率边的位置.当时,所有的态都是局域的.另一种扩展是在跃迁项上做文章[13,14].考虑下面一个紧束缚模型:

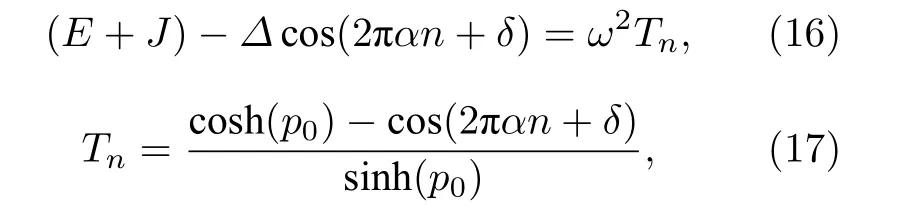
3.2 存在迁移率边的一维准周期光晶格的实验实现

最近,Li等[30]和 Lüschen 等[31]在冷原子系统中成功实现了存在迁移率边的一维准周期光晶格

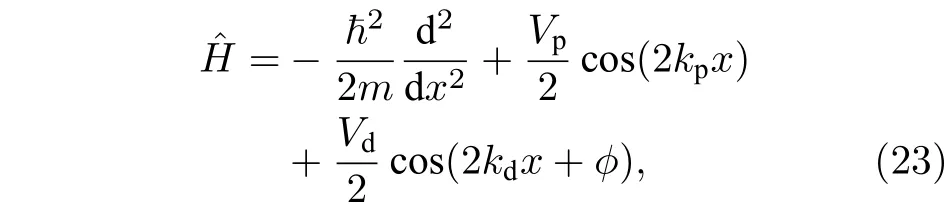
图3 实验原理图.制备的初始 CDW 态，以及在局域、中间和扩展相中，经过一段时间演化后，分别对应的系统的末态 (a)初态分布，制备为CDW态(根据定义，有 ,);(b)局域态 ( , );(c)中间态，对应于不同的能量存在局域态和扩展态 ( , );(d)扩展态( , )Fig.3.Schematics of the experiment.Schematic illustration of the initial CDW state and the states reached after time evolution in the localized, intermediate, and extended phase,respectively:(a)Initial state:CDW state ( ,); (b) localized phase( , ); (c) the intermediate phase,extended and localized states coexist at different energies ( , );(d) extended phase( , ).

这个系统存在三个相:局域相,扩展相和中间相(包含局域态和扩展态的相).实验中为了测得这三个相,他们制备了一个电荷密度波(charge density wave,CDW)的初态,如图 3(a)所示,然后考虑这个初态的演化.如果系统中存在局域态,那么初始的CDW的模式将会存在很长的时间,考虑一个能反映奇偶格点的密度分布差异的量,在很长时间的演化后,它仍不等于零,如图 3(b)和图 3(c)所示.这里,()表示偶(奇)格点的原子数.如果系统中存在扩展态,那么初态会往整个空间扩散,因此原子云的总尺寸将变大.引入可以反映这个变化的量,那么如果系统存在扩展态,将大于零,如图3(c)和图3(d)所示.如果所有的态都是局域的,则等于零,如图 3(b) 所示.如果所有的态都是扩展的,将等于零,如图 3(d) 所示.如果系统中既存在扩展态又存在局域态,那么在一段时间演化之后,和都将不为零,如图 3(c) 所示.在实验中通过测量这两个量,证明了这个系统中中间相的存在,从而间接地说明了迁移率边的存在.

4 存在相互作用的一维准周期系统

安德森局域化考虑的是单粒子的问题,下面加上粒子间的相互作用.相互作用可以影响系统的自能,自能的虚部在一定程度上反映了单粒子激发的寿命,如果单粒子激发在有限时间内可衰减,系统是可热化的,如果单粒子激发有无限长的衰减时间,系统可稳定存在,它是多体局域的,所以相互作用可以影响热化相和多体局域相之间的转变[32].另外,从动力学角度来分析一个封闭的多体系统的初态在任意长的时间内会演化成什么样的态.根据初始态的细节信息会不会在演化过程中消失也可以区分热化相和多体局域相[33].多体局域的系统在任意长的时间演化后都不会热化,从动力学上看它保留了初始态的信息,并且它对于局域的微扰是不敏感的.多体局域在过去几年里被广泛研究[34−37],它正逐渐成为其他理论的基础,比如时间晶体(time crystal),就是通过弗洛凯 (Floquet)周期驱动和多体局域结合定义的[38].人们第一次在实验中观测到多体局域现象就是在一维的准周期晶格中[23].下面先讨论加相互作用的AA模型的相变[20−22].

4.1 存在相互作用的AA模型

考虑在AA模型中加上近邻排斥相互作用的费米子模型,其哈密顿量为[21]:

4.2 一维准周期系统中多体局域的实验实现

实验上第一次观测到多体局域现象的是Schreiber等[23].他们制备的系统是在AA模型上加上在位的相互作用,即

图4 (a) 随 的 变 化 .当 系 统 尺 寸 为 和 时 用 的 样 品 数 是 ,当 时 用 的 样 品 数 是 ,当 时用 的 样 品数是 ;(b) 平均 的 纠 缠熵 和 随 的变化.当 和 时 用 个样 品,当 时 用个样品,当 时用 个样品.相互作用强度始终被固定为 .这里一个样品指的是任选一个初相位 [21]Fig.4.(a) as a function of .Here we use50samples for and ,30samples for ,and20samples for;(b)averaged entanglement entropy and versus .Here we use500samples for and ,100 samples for and 30 samples for .The interaction strength is fixed at .Here a sample is specified by choosing an initial phase [21].

另外,热化相和多体局域相的纠缠熵随时间的变化也明显不同[44,45].多体局域相对应的纠缠熵随时间变化是对数增加的,这是既不同于热化相,也不同于安德森局域态的性质.所以也可以在实验中测量纠缠熵随时间的变化观测系统从热化到多体局域的转变[23].

进一步,Bordia等[46]也成功在二维系统中观测到多体局域现象.最近,Kohlert等[47]还在已经实现的有迁移率边的系统里引入相互作用,并观测到多体局域.这些实验都是在准周期的系统中完成的,并极大地促进了多体局域方面的理论研究.

5 一维准周期系统中的动力学

正如前面提到的,扩展态和局域态在动力学上会表现出明显不同的性质.下面基于AA模型讨论常见的三种动力学方面的研究:系统参数不变的动力学演化,周期驱动和参数突变的动力学演化.

5.1 AA模型的动力学演化

图5 AA 模型中取不同的 时随时间 t的变化的对数-对数图,这里固定 ,跃迁强度 ,以及系统尺寸√Fig.5.Log-log plot of the width vs time t for several values of in the AA model with ,and .

另一个常用来描述AA模型不同相的动力学演化差异的是初态的残存率 (return probability)[53,54],即若假设初态是粒子在某一个格点上,在一段时间演化之后,研究这个粒子还待在这个格点的概率.因为在后面的AA模型的动力学相变中会详细介绍这个量,所以这里不再赘述.

5.2 周期驱动的准周期晶格

考虑下面的准周期势是周期驱动的模型[55]:

图6 固定 和 ,平均信息熵随周期 的变化.左上角的插图展示了平均纠缠熵的导数随周期 的变化 ,这 里 固 定 (蓝 色 ), (红 色 ),和(绿色).右下角的插图展示了平均纠缠熵随 的变化,这里分别固定 (蓝色), (红色), (绿色)[55]Fig.6.The mean information entropy as a function offor this system with and .The left up inset shows the derivative of the mean information entropy as a function of with fixed (blue), (red),and (green). The right down inset shows the derivative of the mean information entropy as a function ofwith (blue), (red),and (green)[55].

由于AA模型中不存在迁移率边,所以可以定义一个平均的信息熵.图6展示了这个平均的信息熵随驱动周期的变化,这里固定了准周期势的强度.可以看出,随着周期的增大,这个平均的信息熵从近似于零的小值变为一个非零的有限值,这意味着这个系统的波函数从局域态变为扩展态.在图6的插图中,展示了不同强度的准周期势时,平均信息熵的导数随周期的变化.当,和时,这个导数 的 尖 峰 分 别 出 现 在,和处.图6下方的插图展示了不同周期时,平均信息熵的导数随的变化,可以看出当,和时,平均信息熵导数的尖峰分别出现在,和的地方.可以看出,平均信息熵导数的尖峰位置满足,这对应于这个系统从动力学局域到扩展的转变点.

下面从这个系统的有效哈密顿量中来分析这个转变点,

5.3 准周期晶格中扩展-局域转变的动力学相变

图7 固定系统尺寸 ,平均信息熵随 和 的变化[55]Fig.7.The mean information entropy versus both andfor the system with [55].

动力学相变最近被广泛研究[62−65],它扩展了我们对相变的理解.第一次在局域扩展的转变中引入动力学相变的概念是在AA模型中[66],即哈密顿量如 (2） 式所示,下面设作为能量单位.制备一个初态,使之是哈密顿量的一个本征态,然后突然改变系统的参数,用哈密顿量描述,研究在一段时间演化后,初态的残存率[67−71]

图8 取不同值时 Loschmidt echo 的演化.初态选准周期势强度为 ((a),(b))和 ((c),(d)) 的哈密顿量的基态[66]Fig.8.Evolution of Loschmidt echo in a long time with different s.The initial state is chosen to be the ground state of the Hamiltonian with ((a),(b))and ((c),(d))[66].

下面对Loschmidt echo怎么趋于零进行定量描述,引入一个接近于零的小量对做截断.给定一个大的时间间隔,在中,测量满足的时间间隔长度,定义为.相当于引入了一个勒贝格测度(Lebesgue measure)[66].为了方便,研究.固定,在图 9(a)中,展示了取不值同时(,,和),随的变化.这里的初 态 仍 然 是 选 系 统 的 基 态 .可 以 看 出,在和时 的 表 现 确 实 不 同 .当时,总是零,但是过了转变点后,它随着的变大突然增大到一个有限的非零值.尽管这个非零值会依赖于截断的的大小,但是这种在转变点突变的性质不会随着截断的不同而改变.

6 准周期势对系统拓扑性质的影响

最近几十年,拓扑态(拓扑绝缘体、拓扑超导体和拓扑半金属)的发展是凝聚态发展的一个重要的方向[72−75].对拓扑相变的描述超出了朗道对称性破缺的理论,加深了我们对凝聚态的认识.如果系统是周期的,可以通过调节跃迁强度的相对大小来诱导拓扑和非拓扑之间的转变[76,77].在开边界条件下,这个转变会对应于边缘态的出现或消失;在周期边界条件下,这个转变可以计算拓扑不变量来描述,这个不变量在实验上可以通过索利斯泵浦(Thouless Pumping)来测量[78−81].如果系统中存在无序或者准周期势,那么一个自然且有趣的问题是它们会对系统的拓扑性质产生什么影响.下面研究在一维p波超导链[82]和外尔半金属[83−85]中增加准周期势对系统产生的影响.

图9 固定系统参数 , 和 时 随 的变 化:(a) 不 同的颜色对应不同的 值,这里的初态是初始哈密顿量的基态;(b)选取不同的初态, 表示初始哈密顿量的第 n个本征态.在 处,可以清晰地看到一个相边界.这里固定 [66]Fig.9.The behavior of versus for the system with , and :(a)Different colors correspond to different s and the initial state is chosen to be the ground state of the initial Hamiltonian;(b)different choice of initial state with standing for the eigenstates of the initial Hamiltonian .A clear boundary can be seen at .Here we choose [66].

6.1 准周期势对一维p波超导链的影响

在一维p波超导链上加上准周期势[16,18,19],讨论其影响.系统的哈密顿量为

这个哈密顿量可以用波戈留波夫-德热纳变换 (Bogoliubove-de Gennes(BDG)transformation)[16,89]来对角化:

图10 (a)固定两个 p 波配对强度 和时，MIPR随准周期势强度 的变化，这里用的系统尺寸是 ;(b)系统随 p 波配对强度 和准周期势强度 变化的相图，I:扩展相，II:临界相，III:局域相.这里固定Fig.10.(a) MIPR as a function of the incommensurate potential strength at two p-wave pairing strengthand .Here use ;(b) phase diagram of this system with a p-wave pairing strengthand incommensurate potential strength .I:extended phase,II:critical phase and III:localized phase.Here fix.

6.2 准周期势对外尔半金属的影响

考虑下面的可在冷原子中实现的外尔半金属模型的哈密顿量[90]:

图11 (a)在开边界条件下,固定 和 时系统的能谱;(b),(c) 不同的 值时最低激发模的 ((b)) 和 ((c)) 的分布[16]Fig.11.(a)Energy spectra of this system with and under OBC.The distributions of (b)and (c)for the lowest excitation with different [16].

这是下带所有本征态的IPR的平均.MIPR可以给出下带所有填充态的扩展到局域转变的信息.图12(a)和图12(b)分别展示了第个本征态的IPR 和 MIPR 作为和的函数,这里取.从图中可以看出,在附近的态是扩展的,而其他区域的态在方向已经变得局域,也就是说附近的态在方向更难变得局域,即需要更大的才能使外尔点附近的态变得局域.图12(c)和图12(d)分别刻画了固定时第个本征态的IPR和MIPR作为和的函数.图 12(e)和图 12(f)展示了固定时第个本征态的IPR和MIPR作为和的函数.从这些图中可以看出在,>时开始有本征态在方向变得局域,而动量在附近的本征态在时才由扩展变为局域.从(40)式出发,可以直观地理解这一现象.A和B子格之间的有效跃迁强度大小依赖于和.A和B子格间的跃迁是在平面内,其跃迁强度越大,粒子在方向的运动就会更容易变得局域,反之,平面内的跃迁强度越小,则方向的运动变得局域所需要的就越大.当和时,从(40)式中可以看出,两个子格间的有效跃迁强度是零,这时粒子在方向的运动发生扩展到局域的转变所需要的最大,而且可以看出这时这个模型可以简化为AA模型,所以时所有方向的本征态变成局域,这和我们的数值结果是一致的.

为了研究系统的费米面随着准周期势增大的变化,下面数值计算态密度 (density of states,DOS),其定义为

图12 第N个本征态的IPR((a))和 MIPR((b))随 和 的 变 化 ,这 里 固 定 ;第 N 个 本 征 态 的 IPR((c))和MIPR((d))随 和 的变化,这里固定 ;第 N 个本征态的 IPR((e)) 和 MIPR((f))作为 和 的函数,这里固定 .其他参数是 和 [91]Fig.12.IPR((a))and MIPR((b))as a function of and with fixed ;IPR((c))and MIPR((d))as a function of and with fixed ;IPR((e))and MIPR((f))as a function of and with fixed .The lattice size is and

图13 (a)不同晶格尺寸 时, 随 的变化,这里固定 ;(b) 固定 ,取不同的准周期势强度 时系统的态密度随能量的变化[91]Fig.13.(a) versus for different lattice size with fixed ;(b)DOS with as a function of energy for various values of incommensurate potential strength [91].

最近,人们还研究了在外尔半金属的三个方向上都加上准周期势[96]以及在节链(nodal-link)半金属的一个方向上加上准周期势[97,98]时系统发生的相变,都得到了一些有趣的结果.

7 总结与展望

当一个新的物理现象被发现的时候,一个自然而有趣的问题就是这种物理现象能否被无序(或准周期势)轻易地破坏,比如前面提到的准周期势对拓扑超导体相和拓扑半金属相的影响.所以对无序(或准周期势)的研究具有持久的生命力.在一维系统或者冷原子系统中,准周期势的优点显得尤为突出:一方面它本身具有很好的性质,比如可解析得到扩展到局域的转变点等,使得对这类模型本身的研究就很有意义,如文中提到的动力学性质的研究;另一方面,这种势在冷原子实验中更容易实现,因此正如文中提到的,第一次实验观测到准周期势导致的局域转变,第一次实验观测到多体局域,第一次实验验证迁移率边的存在等等都是在冷原子中实现的准周期势的晶格中完成的.正是因为在冷原子中实现了很多与准周期势有关的物理现象,反过来又推动了这方面的理论研究.相信在将来,准周期势会被应用到更多的领域,会带来更多有趣的物理现象.本文主要涉及了准周期势带来的局域转变方面的工作,实际上当体系处于扩展态时在准周期格子系统中也展示了丰富的拓扑相,有兴趣的读者可以参考相关的文献[77,99–101].