基于学生发展的教学实践与反思

郁中华

[摘  要] 立足于学生发展并帮助学生在掌握基础知识与技能的基础上灵活运用数学思想方法是数学教学的根本，本文着眼于“数系的扩充与复数的概念”进行了以学生发展为根本的教学设计和思考.

[关键词] 认知冲突;认知顺应;意义;应用;升华

以学生发展为根本并帮助学生在掌握基础知识与技能的基础上灵活运用数学思想方法是数学教学的根本，本文结合《论语》中的“本立而道”这一思想对“数系的扩充与复数的概念”进行了教学设计方面的仔细思考.

教材与学情分析

“数系的扩充与复数的概念”这一章节内容包含了数系的扩充、复数的引入及相关概念. 数的发现与创造、数的发展的现实背景与客观需求都在数系的扩充这一内容中得到了很好的体现. 复数的引入则是中学阶段数系的最后一次扩充. 高中学生学习复数的基础知识能够帮助他们对数的概念形成较为完整的认识并为其问题的解决增添新的工具.

当然，学生在学习这一章节内容时必然也会遇到一些障碍或疑惑，比如，虚数的单位i为何要引入呢？又是怎样引入的呢？复数的意义是什么？它是怎样的数？

教学目标

（1）掌握复数的概念、复数的代数表示、复数相等的重要条件.

（2）在回顾旧知中体会数系扩充的过程与基本方法，对复数相关概念的形成获得理解.

（3）领会虚数引入的必要性并体会人类理性思维的作用，帮助学生建立积极的学习态度.

教学重难点

重点：①数系扩充的过程;②复数的相关概念;③复数相等的充要条件.

难点：①数系扩充的原则;②对虚数单位i的理解.

教学过程

环节1：诱发认知冲突并进入课题的学习

问题1：我校高一、高二年级分别有多少个班级？这两个年级的班级数之比为多少？

设计意图：用熟悉的数字与事件为本课教学进行铺垫，引导学生在数字这一基本语言的运用与研究中体会数系的扩充与壮大.

问题2（当年一道令数学家卡尔丹头疼的问题）：可否把10分成两部分并使这两部分的乘积为40？

设计意图：引导学生在数学历史的回顾中感受数学的魅力，让学生在体会数学大师思想的同时获得问题的答案：“无法找到两个和为10、积为40的实数.”这就意味着方程x2-10x+40=0没有实数解. 追问：“该方程为何无解呢？”“有何根本原因？”“-15不能开方，那何数可以开方并解决所有负数开方的问题呢？”让学生在认知冲突中对问题形成积极主动的思考并顺利进入课题的研究中.

环节2：在认知顺应中扩展数的认识

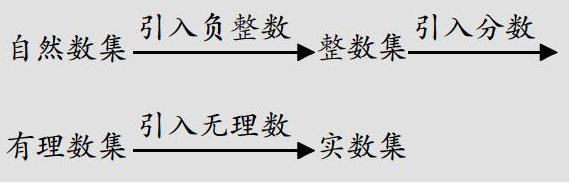
问题3：数系的扩充经历了哪几次？每一次的扩充都解决了原先哪些无法解决的问题呢？

设计意图：学生对数已经建立的认知是本课内容学习的生长点，因此，教师可以首先帮助学生对数系的扩充进行梳理，使学生能够在了解数系扩充的历史序的基础上形成数系扩充的逻辑序，使学生在感受引入新数进行扩充的同时感受数系扩充的社会发展必要性，不仅如此，不够减、不能整除、不能开方等数学内部发展的需要也令数系扩充有了必要性：

问题4：上述数系的扩充所具备的共同特征有哪些？

设计意图：引导学生梳理、归纳数系的扩充并感受其合理性，对数系扩充的一般原则进行梳理与提炼：①引入新数;②原有的运算与性质在新的数集中仍旧适用.

问题5：实数集应如何扩充才能解决负数开方这一问题呢？

设计意图：首先寻找一个平方后能够等于-1的数并将“新元i”顺利引入，然后规定：①i2=-1;②实数能和i进行四则运算，原有的运算法则都能成立并令实数集得到扩充. 然后将新元i的200多年发展史介绍给学生并使其能够领会知识发現过程中的数学思想方法与精神.

环节3：联系意义并帮助学生掌握复数

问题6：实数与虚数单位i进行四则运算后可得到新的数，大家能举例后归纳出其一般形式吗？

设计意图：引导学生运用新知列举出含有i的新数并进行思考：“所列举出的数字中哪些可以归为一类呢？大家以为其一般形式是怎样的？”学生一般都能先发现bi，继而发现a+bi（b≠0），不过学生一般都会将实数遗漏. 笔者进行了追问：“能产生2，3…吗？”“大家以为哪种形式可以将刚才所列举出的数都包含进去呢？”学生在教师的引导下从特殊到一般并将复数的代数形式a+bi（a，b∈R）概括了出来，学习复数的相关概念的同时也很好地完成了实数集到复数集的扩充. 笔者又及时地进行了追问：“大家觉得我们所列举的复数的实部与虚部都是什么呢？”“能对复数进行分类吗？”“分类的依据是什么呢？”学生在教师问题的引导下很快联想到实数a，b的不同取值并对复数进行了分类，即

复数实数，b=0，虚数，b≠0.

复数的概念在如此的经历中得以深化，本课的重点也因此得以攻克，数系也因此顺利得以扩充.

环节4：引导学生在精选的练习中掌握应用

例1：判断以下命题的正确性：

（1）若a，b是实数，则z=a+bi为虚数;

（2）若b是实数，则z=bi为纯虚数;

（3）若b=0，则z=a+bi为实数.

设计意图：在学生自主归纳出复数的分类之后设计上述诊断的练习题能帮助学生及时巩固对这一知识点的理解.

例2：用韦恩图表示数集N，Z，Q，R，C之间的关系应如何表达？

设计意图：这一例题的设计主要为了前后照应并令学生在概念同化的练习中对认知结构进行完善，使学生能够在数系扩充的过程中对知识点形成更好的理解.

例3：实数m取何值时，复数z=m（m-1）+（m-1）i是（1）实数？（2）虚数？（3）纯虚数？

设计意图：引导学生對复数的分类标准进行熟悉并同时内化复数的有关概念，使学生能够在实际问题的解决中及时巩固知识、反馈学习的具体状态. 在学生解决例3之后可以进行追问：上述例题中的m取何值时，复数z为0？是6+2i？学生根据已有知识经验往往能够自主解决并获得复数相等的概念.

例4：已知（x+y）+（x-2y）i=（2x-5）+（3x+y）i，实数x，y的值是多少？

设计意图：令学生在实际问题的解决中强化复数相等的充要条件并感受复数问题向实数问题的化归.

环节5：在小结中理性升华

大家在本课的学习中学到了什么？

设计意图：教师在学生总结的基础上进行提炼并因此形成总结的模式，帮助学生养成总结与反思的习惯.

教学反思

1. 数学文化渗透课堂始终

常见的数集到数学家卡尔丹的问题令学生感受到了数学发展的漫长历史，“i”这一经历两个世纪才为人接受的虚数单位的出现也将更加广阔的数学天地展现在大家眼前，学生学习数学知识的同时也感受到了浓厚的数学文化气息.

2. 数学方法贯穿课堂始终

以学术形态存在的数学学科蕴含着丰富的思想方法，学生记忆、理解、把握数学知识的同时还应对以知识为载体的数学思想方法进行深刻的领会.

笔者在此课的设计中利用问题串将数的发展历史进行了展现，学生在数系的扩充这一知识的发生过程中进行思考与创造并抽象概括出了数系扩充的原则. 类比实数的分类引导学生对复数的分类进行思考，使学生在复数分类的思考中实现了数系的扩充、复数的分类并因此体会到了新旧知识在研究方法上的一致性.

3. 学生活动串联课堂始终

学生对所学知识形成理性的理解必须建立在丰富的感性体验的基础之上，虚数的“生长”过程对于学生来说是一个从无到有、从疑惑到接受、从模糊到清晰的过程，学生在教师精心设计的活动中亲身经历知识的发生与发展并令自身的认知从片面过渡向完善，复数是什么、引入复数的必要性、如何引入、引入后的作用等疑惑也因此在活动中一一消除.

本课设计中的学生活动主要有两次. 笔者首先引导学生回顾了从小学开始依次遇到的数集，令学生在思考数集扩充原因的基础上对每一次扩充所解决的问题进行了深入的思考，并在学生深入思考的基础上组织了学生小组的交流与合作. 第二次活动是围绕虚数单位i和实数所构成的新数来进行的，组织学生进行小组讨论与合作学习中设计了以下问题：①从形式看，这些新数的特征有哪些？②能描绘其一般形式吗？③如何分类？学生在这两次的活动与探究中很快自主获得了概念，学生的科学品质与创新精神在活动的参与和教师的指引中获得了有意义的锻炼与塑造.