地下气化热 -力耦合作用下短壁工作面长度的确定方法
2019-03-13黄温钢王作棠邬书良张修香严荣富
黄温钢,王作棠,邬书良,霍 亮,张修香,严荣富
(1.东华理工大学 地球科学学院,南昌 330013;2.中国矿业大学 煤炭资源与安全开采国家重点实验室,江苏 徐州 221116)
煤炭地下气化(以下简称“地下气化”)是一项通过化学方法实现固体煤炭资源流态化开采的技术,可用于开发资源储量巨大的深部、关闭/废弃矿井煤炭资源,较传统采煤方法具有更好的安全性、环保性和适应性[1-3]。然而,随着气化工作面的推进,燃空区逐渐扩展导致顶板大范围垮落,可能引起煤气泄漏、地下水溃入和地面塌陷等问题,从而影响产气稳定性,危害气化区邻近水体、生态环境、人员、设备以及构筑物等安全。因此,燃空区围岩稳定性控制是地下气化的关键技术之一。
相关学者针对地下气化燃空区覆岩破坏机理和围岩稳定控制等进行了研究。余峰[4]通过实验发现气化通道周围煤体在高温作用下形成干馏组合碹,其承载能力和整体稳定性较煤体有所提高,并据此提出利用地下气化回收三下煤炭资源的设想。陈启辉[5]建立了地下气化燃空区岩层扩展数学模型,并提出利用湿式充填法来控制燃空区的稳定性。谭启[6]建立了地下气化岩石弹性固-热耦合和弹塑性固-热耦合控制方程,发现高温条件下两模型计算所得的最大等效热应力相差较大。郑慧慧等[7-8]通过数学建模和数值模拟研究发现,地下气化顶板岩层下沉速度比常规开采的下沉速度快,且垂直位移较大。陆银龙等[9]建立了考虑岩石损伤演化的温度-应力耦合作用控制方程,现场实测发现气化高温在燃空区覆岩中的影响范围约为19 m,覆岩的最大断裂带发育高度约为28 m.唐芙蓉等[10-11]建立了温度-应力耦合作用下的燃空区覆岩关键层力学模型,发现考虑温度因数时,煤层顶板具有更大的初次来压步距、周期来压步距和较小的冒落带高度。上述研究主要针对长壁开采法;由于在燃空区内难以形成有效支护体,使用该方法进行开采的过程中可能发生顶板大面积垮落,从而影响气化过程。
与传统物理采煤方法相比,地下气化工作面无大型设备,采用短壁或条带开采法其布置更加灵活,且更有助于深部采场围岩稳定性控制,更加适应深部、残留煤炭资源赋存特点。在地下气化短壁开采方面,部分学者也开展了一些有益探索。王作棠等[12]提出了工作面老顶初次来压步距的计算预测法,认为当工作面长度小于其顶板步距准数时,将形成短壁工作面或巷道情形,理论上老顶将不垮落。XIN et al[13-15]以地下气化短壁工作面为研究对象,提出了以包络线作为围岩烧变范围、焦化圈范围及温度影响范围计算依据的新方法,并建立了含温度场的多层热弹性基础梁模型。WANG et al[16]建立了温度场在顶底板、气化煤层内的一维热传导方程,发现顶底板围岩及周围煤层内各点温度呈现先增大后减小的趋势。这些研究主要集中在围岩温度场、覆岩移动与地表变形规律等方面,关于地下气化短壁工作面长度的确定方法则尚未涉及。传统短壁工作面长度或条带采宽通常采用经验方法确定[17],一般为采深的1/4~1/10.由于未考虑温度影响,该方法并不适用于地下气化短壁工作面长度的确定。
本文针对地下气化燃空区覆岩处于高温和地应力耦合环境的特点,基于燃空区顶板稳定性控制目的,建立了地下气化顶板极限跨距计算式,并提出了地下气化热-力耦合作用下短壁工作面合理长度的确定方法。
1 地下气化短壁工作面长度确定方法
地下气化燃空区顶板同时受到地应力和高温作用。为便于计算,先分别对顶板所受的地应力和热应力进行单独分析,再进行应力叠加。
1.1 仅地应力作用下的工作面长度确定方法
为维持短壁工作面顶板的稳定性,应控制工作面长度小于其直接顶或老顶的极限跨距。短壁工作面顶板三维空间模型可简化为平行于工作面方向的二维平面问题。同等情况下,由简支梁模型计算所得的极限跨距比固支梁模型计算的小,而弯矩形成的极限跨距又比剪切应力形成的小[18]。为安全起见,采用简支梁计算,模型如图1所示。
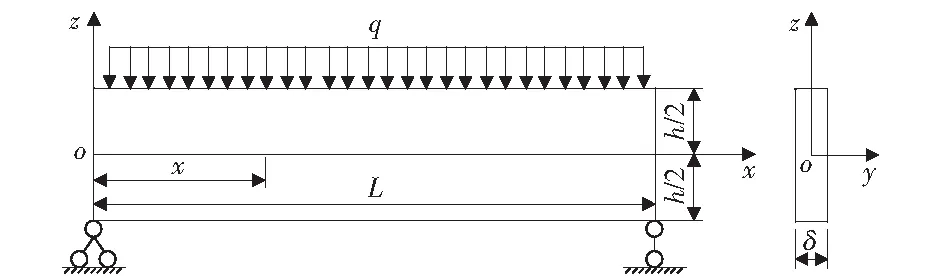
图1 顶板简支梁模型Fig.1 Simply supported beam model of roof
1.1.1 顶板应力分析
以最大拉应力作为岩层断裂的依据。此时,最大弯矩Mmax发生在梁的中间,即
(1)
式中:Mx为简支梁x点处的弯矩,N·m;q为岩梁承受的载荷,N/m2;δ为岩梁y轴方向的厚度,m;L为岩梁长度,m;h为岩梁厚度,m.
已知梁所受最大弯矩Mmax发生在梁的下边缘中间处(z=-h/2),则该点的最大拉应力σmax如下:
(2)
式中:Iy为对称中心轴断面矩,m4;h为岩梁厚度,m.
1.1.2 顶板极限跨距
根据拉破坏准则,当σmax=σt,即岩层所受拉应力达到其极限抗拉强度时,将发生破坏,可得其极限跨距LlT:
(3)
式中:σt为岩层极限抗拉强度,MPa.
综上,若要维持短壁工作面直接顶的稳定性,工作面长度We应满足:
(4)
若要保证短壁工作面老顶或覆岩关键层不发生破断,还应考虑顶板垮落角对工作面长度的影响,即
(5)
式中:Ht为顶板关键层下表面至煤层上表面距离,m;ψ为顶板垮落角,一般取45°~75°.
计算短壁工作面顶板极限跨距LlT之前,需先确定顶板所受载荷q.顶板任一岩层所受荷载包括其自重及其上覆邻近岩层产生的载荷。假设开采煤层直接顶控制其上部n层岩层,则其上部n层岩层将与第1层(直接顶)发生同步变形,形成“组合梁”。将n层对第1层形成的载荷用qn,1表示,则有[18]
(6)
式中:γi为上部第i层岩层的容重,kN/m3;hi为上部第i层岩层的厚度,m;Ei为上部第i层岩层的弹性模量,GPa.
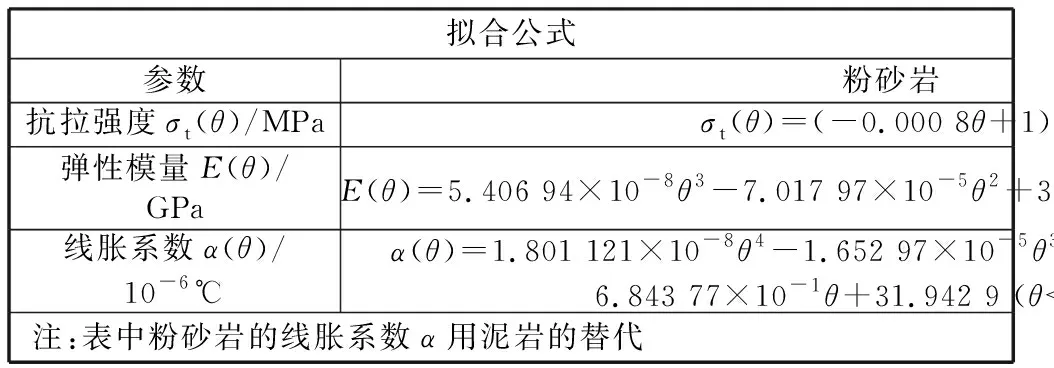
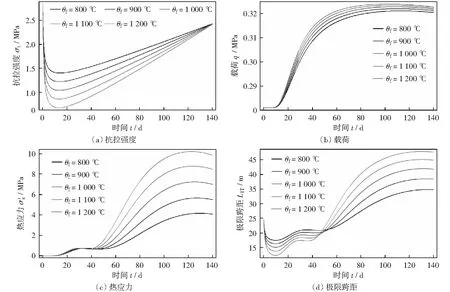
运用式(6)自下而上逐一计算上部n层岩层对第1层形成的载荷qn,1.若计算至n+1层时,出现qn,1 先确定燃空区顶板内的温度分布规律,据此计算顶板岩层内的热应力;再与常温状态下计算的拉应力进行叠加,通过叠加应力计算顶板的极限跨距;在此基础上确定气化工作面的合理长度。 1.2.1 顶板温度分布 为掌握燃空区顶板内的温度分布情况,先需确定不同时刻和位置处顶板下表面的温度。为便于计算,假设燃空区内充满各向同性介质,且除火焰工作面外无其他热源,则燃空区顶板下表面某一处温度可假设为时间t的线性函数θsp(t): θsp(t)=θf-kt. (7) 将燃空区上部所有岩层视为一无限厚顶板,则其内部温度θro关于距离z和时间t的分布函数为[22] (8) 1.2.2 顶板热应力 (9) 式中:α为岩梁线胀系数,1/℃;E为岩梁弹性模量,MPa;θ(z)为岩梁弯矩最大处的温变,℃. 式(9)中,第一项为z轴方向温变导致的x方向产生的热应力,第二项为假设距离梁端足够远处截面上产生的一个近似均布的拉应力,第三项为当θ(z)对x轴不对称时产生的力矩。式(9)适用于梁端无约束的情况[23]。此处,简支梁两端受约束,即梁受热后无法沿x方向伸长,但能弯曲。故可略去第二项,则式(9)变为 (10) 因此,对于地下气化而言,燃空区顶板岩梁中间下边缘的最大拉应力为 (11) 1.2.3 燃空区顶板极限跨距 (12) (13) 而当要维持稳定性的顶板距离煤层较远时,应考虑顶板垮落角对工作面长度的影响,则有 (14) 需要注意的是,上式中σt、α、E和q等参数的取值应考虑到温度的影响。 以贵州盘江某矿煤炭地下气化工程为例。该工程设计采用有井式富氧蒸汽连续法气化工艺,用于开采具有突出危险性煤层。气化首采工作面位于该矿4号煤层采四区南翼1043工作面的东北部,地下气化区钻孔柱状图如图2所示。根据上述方法,首先确定燃空区顶板温度分布规律,再计算顶板的极限跨距,最终确定气化短壁工作面的合理长度。 通过式(8)可计算出顶板的温度分布情况,参数取值如下:火焰工作面的总运行时间tr=136 d;不同气化工艺条件下火焰工作面的温度变化范围为θf=800~1 200 ℃;围岩原始温度θo=20 ℃;顶板岩层的导温系数a=5.26×10-7m2/s;燃空区温度分布函数斜率k=5.11×10-5℃/s(800 ℃时)或8.51×10-5℃/s(1 200 ℃时);开切眼处顶板的最终冷却温度θc=200 ℃.将上述参数代入式(9),采用Mathematica软件进行计算,并绘制了燃空区覆岩内不同时刻温度的分布曲线,如图3所示。 图2 地下气化区钻孔柱状图Fig.2 Drill column in UCG zone 图3 不同时刻燃空区顶板内温度分布曲线Fig.3 Distribution curves of temperature in the roof of the combustion space area at varying times 计算结果表明:随着火焰工作面的推进,靠近顶板下表面0~3 m处岩体温度先迅速上升、后逐渐下降,而3~10 m处岩体温度则缓慢上升;对于不同气化工艺,虽然火焰工作面的最高温度有所不同,但高温对顶板岩层的影响范围仅为10 m左右。 根据气化区柱状图(图2),将岩层参数代入式(6),可计算出不考虑温度作用下的上覆各岩层对4号煤层直接顶所形成的载荷。各岩层参数和载荷计算结果详见表1。由表1可知,4号煤层直接顶所受载荷来自其上覆5层岩层(包含直接顶自身)。 表1中列出了常规煤岩物理力学参数,而计算燃空区顶板的极限跨距时应考虑高温对煤岩物理力学特性的影响。由图3可得,地下气化高温在覆岩中的影响范围小于10 m,即仅对4号煤层上覆临近的3层煤、岩层产生影响。燃空区顶板极限跨距计算式中涉及的受温度影响较大的物理力学参数包括抗拉强度σt(θ)、弹性模量E(θ)和线胀系数α(θ).调研相关文献[11,24],获得了粉砂岩和煤相关参数随温度变化的拟合公式,见表2。 表1 4号煤层直接顶所受载荷计算参数Table 1 Calculation parameters of load on immediate roof of No.4 coal seam 各岩层的温度是随时间变化的,其物理力学性质也随之改变。为简化计算过程,计算各岩层物理参数时,其温度直接取各层平均值(即中间值);为减少顶板垮落程度,在计算顶板抗拉强度时,温度取其邻近下表面区域的温度值。因此,由式(8)可得直接顶(粉砂岩和泥质粉砂岩互层)下表面及直接顶、煤、粉砂岩和细砂岩互层等三层岩层中间的温度关于时间的函数,分别为θro(0.2,t)、θro(3.35,t)、θro(7.20,t)和θro(9.68,t).将各式代入表2中粉砂岩和煤的抗拉强度、弹性模量、线胀系数随温度变化的拟合公式,再将其代入式(6)、(10)和(12)中,可得到不同气化工艺条件下,燃空区直接顶的抗拉强度、载荷、热应力和极限跨距随时间的变化情况。采用Mathematica软件计算并绘制了不同气化工艺条件下燃空区直接顶的抗拉强度、载荷、热应力和极限跨距随时间的变化曲线,如图4所示。 表2 粉砂岩和煤的热物理及力学参数的拟合公式Table 2 Fitting formula of thermal physical and mechanics parameters of siltstone and coal 图4 燃空区直接顶抗拉强度、载荷、热应力和极限跨距随时间的变化曲线Fig.4 Curves of tensile strength, load, thermal stress and ultimate span of immediate roof of the combustion space area with time 由图4可知:对于不同地下气化工艺,随着火焰工作面的向前推进,燃空区直接顶承受的载荷和热应力在稳定了一段时间之后迅速上升,而抗拉强度则先下降、后上升;三者的共同作用,导致直接顶的极限跨距并非一个定值,而是呈现先小幅下降、后急剧上升的变化趋势。这是由于气化过程中覆岩体内同时产生了逐渐增大的垂直和水平方向的热应力,前者增加了直接顶所受载荷,使其产生更大的拉应力,但后者会抵消部分拉应力(相当于在顶板内施加了一水平应力);直接顶所受载荷大幅上升的时间(10 d左右)早于水平热应力大幅上升的时间(40 d左右),故前期直接顶的极限跨距出现了小幅度降低现象,后期随着水平热应力和直接顶抗拉强度的同时增加,直接顶的极限跨距又迅速上升。 鉴于地下气化过程中燃空区顶板的极限跨距并非定值,为最大限度维持其顶板稳定性,地下气化短壁工作面长度应小于图4(d)中直接顶极限跨距变化曲线的最小值,即气化短壁工作面的合理长度不应超过12 m.故该项目气化短壁工作面的长度取12 m. 1) 针对地下气化燃空区覆岩处于高温和地应力耦合环境的特点,推导出了燃空区直接顶热应力和极限跨距的计算公式,构建了地下气化短壁开采的合理长度确定方法。 2) 以贵州盘江某矿煤炭地下气化工程为例,计算结果表明,随着火焰工作面的推进,距离顶板表面0~3 m处岩体温度先迅速上升、后逐渐下降,而3~10 m处岩体温度则缓慢上升,地下气化高温在覆岩中传播范围有限,仅为10 m左右。 3) 地下气化过程中,燃空区直接顶承受的载荷和热应力在经历一段时间稳定不变后迅速上升,而抗拉强度则先下降、后上升。在三者的共同作用下,直接顶的极限跨距呈现先小幅下降、后急剧上升的变化趋势。 4) 由于地下气化过程中燃空区顶板的极限跨距并非定值,为最大限度地维持燃空区顶板的稳定性,气化短壁工作面长度应小于直接顶极限跨距变化曲线最小值。由此得出贵州盘江某矿煤炭地下气化工程的气化短壁工作面的合理长度为12 m.这说明该方法可为地下气化工作面长度设计提供理论指导。1.2 热-力耦合作用下工作面长度的确定方法
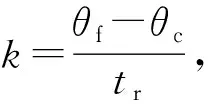
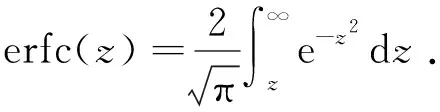
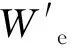

2 工程设计实例
2.1 燃空区顶板温度分布规律


2.2 燃空区顶板极限跨距

3 结论
