一种利用相关性度量的不确定数据频繁模式挖掘
2019-03-13任永功张志鹏
任永功,高 鹏,张志鹏
(辽宁师范大学 计算机信息与技术学院,辽宁 大连 116029)
1 引 言
随着数据收集和存储技术的进步,产生了海量数据.其中,现实生活中产生的不确定数据受到了广泛重视,继而对不确定数据频繁模式挖掘的需求日益增长,然而从中提取有用的信息已经成为巨大的挑战.
频繁项集[1]挖掘作为数据挖掘方面的基础步骤,在不同领域都出现了许多有效的方法.比如项集挖掘[2,3](例如Apriori,FP-growth),数据流挖掘[4],序列模式挖掘,频繁图挖掘,高效用模式挖掘[5],相关模式挖掘[6](例如兴趣度方法),行为挖掘和时序数据挖掘.其中多数方法仅是基于支持度来剪枝组合搜索空间,另外加上确定数据库与不确定数据库在计算上和语义上的差异致使它们并不适用于不确定数据库.
近些年已经提出了不少算法[7-14](例如FOCUS,U-Apriori,UF-growth,UFP-growth,CUF-growth,PUF-growth, TVDBSCAN,WUIPM等)来进行不确定数据库中的模式挖掘,其中也涉及到不确定数据库中一些有效的聚类算法[15,16].其中CUF-growth算法通过引入限值而获得一个紧凑树结构,其性能优于UFP-growth算法,但会产生许多误报信息.于是,PUF-growth算法在树的前缀分支引入限值进而减少误报来成功减少运行时间.所有这些都集中在不确定数据库频繁模式挖掘.然而,频繁模式往往在数量上巨大并且在很多时候包含过多冗余信息,但项之间的相关分析可以在已挖掘的模式中消除冗余和不重要的项集.
此前,WIP[17]和Hyperclique Miner[18]挖掘相关模式和加权相关模式表现突出,但是确定数据库和不确定数据库之间的基本区别使这些方法在不确定的数据库中已经过时.因此,探究新的方法来从不确定的数据库中挖掘相关模式,将更具有价值.
本文将充分考虑项集各项之间的相关性来发现不确定数据中有价值的模式,其中考虑到了每一项的重要性并赋予其相应的权重值代表其项的重要性.
2 相关工作
确定数据库和不确定数据库存在语义上的差异,所以在不确定的数据库中通常用一个项集的期望支持度来代替实际的确定数据库的支持度.目前已经有了许多从不确定数据库中挖掘频繁项集的算法.其中,CUF-growth*[9]介绍的紧凑树和快
速挖掘算法,其性能优于其它算法.然后,提出的PUF-growth算法[12],其采用依赖于前缀分支的树型结构来挖掘频繁模式.所有这些方法只适用于挖掘频繁模式,并且未解决数据挖掘的一个有价值的问题,即频繁项集内各项目之间的相关性.在一般情况下,频繁项集可以是大数量的,它们之间的相关性分析可以删除大量的不相关项集,选择最有效的项集进行知识挖掘.在本节中,按时间顺序对现有的方法进行一个简短的讨论.
首先,U-Apriori[8]算法扩展了Apriori[2]算法,来从一个不确定的数据库中挖掘频繁模式.相对于Apriori算法它有类似的缺点,例如,过度的候选集生成.在U-Apriori之后,提出了基于FP-growth[3]的方法,即UF-growth[9]算法.UF-growth算法使用一棵被称为UF-tree[8]的树结构来存储一个不确定数据库,并从树中挖掘频繁模式.在构建UF-tree[9]的过程中,首先找出期望支持度计数大于或等于最小支持计数的频繁1-项集.然后,在不确定的数据库中每个事务更新只保持频繁1-项集.UF-tree[9]的构造过程就像建造FP-tree[3]除了有着不同存在概率的相同项被放在了不同的节点.而在事务中只有相同的存在概率的相同项才合并在一起.为了进一步减小UF-tree的大小以获取挖掘效率,UFP-growth[10]把相似的节点(即节点具有相同的项X和相近的存在概率值)分成一簇.此簇包含其成员之间最大存在概率值的项X以及其成员的数量.因此,如果没有集群可以形成,UFP-tree[10]可能和UF-tree同样大.另外,它可以减小树的规模,但它可能会产生一个模糊的结果(误报频繁项集).
之后,CK Leung提出CUF-growth[11]和CUF-growth*[12],显著减小了树的规模,达到了比其它不确定数据库中频繁项集挖掘算法更好的性能.虽然CUF-growth*[11]优于所有现有的方法,但它还是避免不了会产生过多的误报信息.因此,CUF-growth*[11]的性能很大程度上取决于其产生的误报数.
目前,为了降低UF-tree[9]和UFP-tree[10]的大小,CK Leung又提出了基于前缀上界的不确定频繁模式树结构(PUF-tree[12]),并可从其中获取不确定性数据的重要信息,进而可以从中挖掘频繁模式.
3 相关描述和问题定义
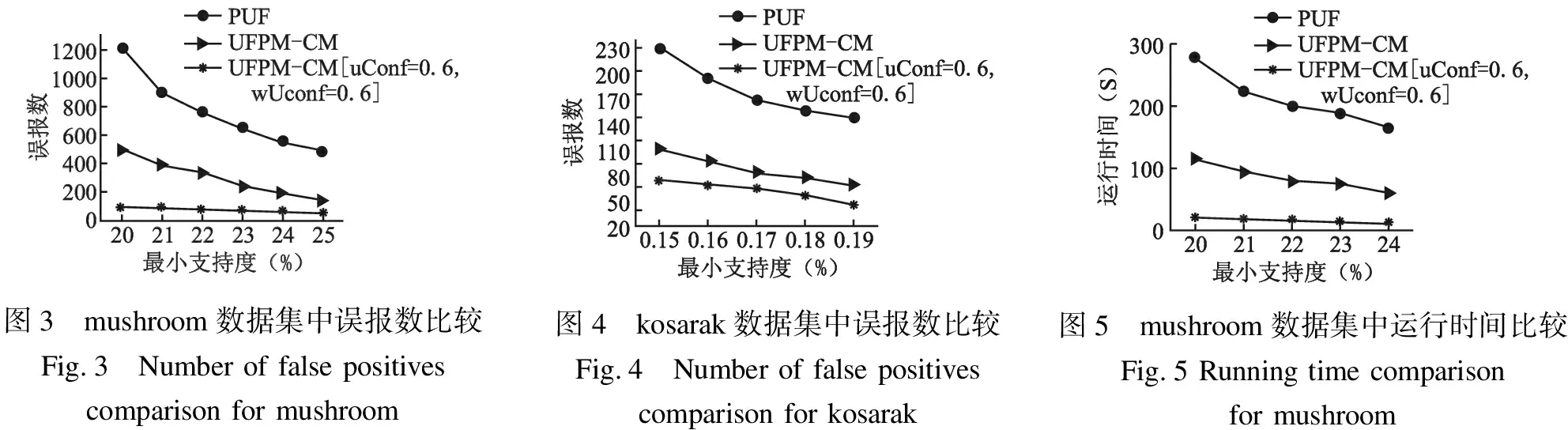
定义1. (前缀).事务ti为{a1:p1,a2:p2,…,aj-1:pj-1,…,an:pn},则定义事务ti中的数据项aj的前缀为p(ti,aj)={ak:pk|ak:pk∈ti,且1≤k (1) 定理1.事务ti任意k-项集(k>2)I={a1:p1,…,ak:pk} 的存在概率总是小于等于其事务前缀上界TpCap(ti,ak),即P(I,ti)≤TpCap(ti,ak). 定义3.(事务前缀代理).ti中项aj的事务前缀代理值记作TpProxy(ti,aj)其值为p(ti,aj)中的第三大概率值.在事务ti={a1:p1,a2:p2,…,aj:pj,…,an:pn}中h=|p(ti,aj)|表示其前缀长度,第三大值M-3=thirdmaxw∈[1,h](pw)则 (2) 定义4.(前缀代理).在数据库T中具有相同p(ti,aj)的事务ti的集合记为TP,在TP中取所有事务第三大值M3中的最大值记为项aj的前缀代理值pProxyk(aj).则 pProxy(aj)=maxti∈TP(TpProxy(ti,aj) ). (3) 定义5.(期望支持度前缀上界).项集X的期望支持度前缀上界记为ExpSuppCap(X),定义如下 (4) 定理2.项集X的实际期望支持度总是小于等于X的期望支持度前缀上界,即ExpSup(X)≤ExpSuppCap(X). 假设这些不确定数据库包含事务ti,ti表示n项集合{a1:p1,a2:p2,…,an:pn},其中每一项aj对应着一个概率值Pj(0 (5) 式中|T|表示不确定数据库中事务的数量,P(x,ti)是项x在事务ti中存在的概率.如果某一项集的期望支持度大于等于预定阈值,则它可以被认定为频繁的. 然而,在不确定数据库中,仅仅依靠期望支持度并不能准确地估计频繁模式,其丢失了项集支持度的不确定性产生误报.继而针对不确定数据库又提出了概率频繁模型[19],假设最小支持度minsup和频繁概率阈值τ,如果 P(sup(X)≥|T|×misup)≥τ (6) 式中sup(X)表示不确定数据库T中包含X的事务数量,满足上式则X被认定为频繁项集. 在本文中,提出了一种新的针对不确定数据挖掘的树结构-UFPM树和对应的快速挖掘算法-UFPM-CM算法,其中考虑到了每一项的重要性并给予相应的权重值代表其项的重要性.引入不确定数据库的度量不确定置信度(uConf)和加权不确定置信度(wUConf)进行项集之间的相关性分析,以删除大量的不相关项集,得到最有效的项集进行知识挖掘. 在不确定数据库(UD)中,|UD|表示事务数量.假定事物之间相互独立,每个事务ti包含多个数据项k,p(k∈ti)∈[0,1]表示数据项k在事务ti中的存在概率.一个不确定数据库样例如表1所示. UFPM树的构建分两步来完成.第一步通过扫描数据库得到频繁项的集合,第二步使用这些频繁项集构造UFPM树.一般来说,一次读取一个事务并将其频繁项插入作为树的一个分支.在插入的过程中,前缀上界TpCap(定义2)和前缀代理值pProxy(定义4)也逐步被计算出来并存储在相应的结点中. 表1 带权值的数据库样例Table 1 Example database with weight 例如在表1中,数据库有6个事务{a1,a2,…,a6},设定最小支持度阈值为38%,则最小支持度计数为0.38×6=2.28.在事务t1中项a的不确定值为0.6,于是项a的期望支持度ExpectedSupport({a}=p(a,t1)+p(a,t2)+p(a,t3)+p(a,t4)+p(a,t5)+p(a,t6)=0.6+0.5+0.4+0.9+0.7=3.1.则扫描数据库,计算出所有项的期望支持(a:3.1,b:3,c:3.3,d:2.9,e:3,,f:3.7).然而通常不确定数据库包含了项集支持度的不确定性,其对项集是否频繁十分重要.根据文献[19],设置合适的频繁概率阈值τ为0.9,计算各项的支持度概率.其中发现项目b和项目e期望支持度相同,但从表2所示的支持度概率分布可以看出,根据公式P(sup(X)≥|T|×minsup)≥τ则e的频繁概率为0.702(=0.534+0.12+0.048),b的频繁概率为0.91(=0.82+0.08+0),这样项e的存在和不存在相较于项b更加明确,然后删除不频繁的项,按期望支持度递减排序到列表Item-list中.这样,结果Item-list={f:3.7,c:3.3,a:3.1,e:3,d:2.9}. 第二步再次扫描数据库,事务插入到树中作为其分支,其中每个项所需要的信息将一个个计算出来.例如,第一个事务t1={a:0.6,c:0.4,d:0.9,e:1,f:0.7}被读取,其中所有不频繁项被移除.然后按Ttem_list中的次序排序得到{f:0.7,c:0.4,a:0.6,e:1,d:0.9}.现在这些项就被插入到树中,并且根据定义2、定义4,相应的前缀上界TpCap和前缀代理值pProxy也被计算出来.具体细节如下.在第一个事务中,f:0.7首先插入空树,其前缀p(t1,f)={φ},所以,TpCap(t1,f)=∞,pProxy(f)=0.接下来,c:0.4作为f(∞,0)的孩子插入,其p(t1,c)={f:0.7},则TpCap(t1,c)=∞,pProxy(c)=0.然后a:3.1作为c(∞,0)的孩子插入,其p(t1,a)={f:0.7,c:0.4},则TpCap(t1,a)=0.7*0.4*0.6=0.168,pProxy(c)=0.如此,{e:1,d:0.9}同上一样插入树中.图1描述了t1插入树中的过程. 所有的事务都以上述方式插入树中,当遇到共享的前缀时,对于前缀上界值与结点已存在的值相加,而前缀代理值pProxy则更新为其最大值.例如,当事务t2插入到树中后,树更新为{f:∞:0,c:∞:0,a:0.168+0.1:0,e:0.42+0.02:0.8,d:0.63+0.06:0.6}.同样,样例中所有事务插入到树中后,得到的树如图2所示. 对UFPM树的挖掘过程分为3个步骤: 1)构建项集投影树; 2)利用剪枝策略过滤投影树; 3)挖掘所需要的项集. 首先,初始频繁项集取自上面的结果集Item-list.UFPM-CM算法对result中的每个项递归地执行这3个步骤,直到产生所有的频繁项集.详细描述见算法2. 图2 最终构建的树Fig.2 Final tree construction 受全置信度的启发引入不确定数据库的度量不确定置信度(uConf)和加权不确定置信度(wUConf),即项集I满足置信度uConf(I)和wUConf(I),那么中的所有规则至少有一条规则也满足置信度阈值,也就是意味着uConf和wUConf隐含着项集中各项之间的相关性,而不是其中两个项之间的相关性,所以一项集只要满足相应的阈值就可以挖掘出强相关的模式. 根据文献[20]所提出的全置信度,提出不确定期望支持度置信度前缀上界和加权不确定期望支持度置信度前缀上界可分别定义如下. 定义6.在不确定性数据库中模式的不确定性置信度前缀上界uConfpCap可表示为: (7) 性质1.(uConfpCap的反单调性):如果模式Z的uConfpCap不小于最小阈值,那么Z的所有子集的uConfpCap值也不小于最小阈值. 定义7.在不确定性数据库中模式的不确定性置信度前缀上界wUConfpCap(Z) 可表示为: (8) 性质2.(wUConfpCap的反单调性):如果模式Z的wUConfpCap不小于最小阈值,那么Z的所有子集的wUConfpCap值也不小于最小阈值. 如果项集Z的uConfpCap(Z)和wUConfpCap(Z)值小于最小阈值,则就无须更深地挖掘它的超集,进而可以有效地剪枝无用的项集.利用UFPM树来简单有效地计算任意项集I的uConfpCap(Z)和wUConfpCap(Z)值,并可以把它们单独地加入到UFPM-CM算法中.因此,除了频繁模式之外,UFPM树可以提取到相关模式,而不需要任何大量的计算. 算法1.构建UFPM树 输入:不确定数据库UD,最小期望支持度阈值δ,频繁概率阈值τ 输出:UFPM树 begin 1. foreach itemI∈UD do 2. Calculate expected supportI; 3. CalculatePi(I); 4. If ExpectedSupport(I)<δthen 5. RemoveI; 6. If P(sup(I)≥N×δ)<τthen 7. RemoveI; 8.Item-list:=Arrangeitemsinapre-definedorder; 9.CreatetherootnodeR; 10. Foreach transactionTi∈UD do 11. Delete all infrequent items fromTi; 12. IfTi≠NULLthen 13. SortTiaccording to the order in Item-list; 14. Insert transactionTi; end 算法2.挖掘强相关模式 输入:UFPM树,最小期望支持度阈值δ 输出:加权强相关项集 begin 1. foreach itemα∈Item-list do 2.Pα= ProjectTree(UFPM-tree, α); 3. Mine(Pα,α,Item-listα,{α}); 4. end 5. ProjectTree(UFPM-tree,α) 6. foreach nodeNα∈UFPM-tree do 7.pathα:=ProjectNα; 8. foreach nodePNα∈pathαdo 9. Calculate PNα·TpCapand PNα·pProxy∈projected treePα; 10. returnPα; 11. Mine(Pα,α,Item-listα,candidate) ; 12. Set candidate as candidate frequent itemset; 13. foreach β∈Item-listαdo 14. ifExpSuppCap(β)<δoruConfpCap(β) then 15. PruneTree(β,Pα); 16. Item-listα=Item-listα-β; 17. ifPα≠NULLthen 18. foreach itemβ∈Item-listαdo; 19. nextCandidate=candidate∪β; 20.Pβ=ProjectTree(Pα,β); 21. Mine(Pβ,β,Item-listβ,nextcandidate); 22. PruneTree(β,Pα) ; 23. foreach nodeNβ∈Pαdo 24. ifNβ·parent≠NULL then 25. foreach st∈Nβdo 26.Nβ·parent:=Nβ·parent∪st; 27. Merge duplicate children; 28. DeleteNβ; end 上述过程中,每一项α,投影树Pα通过ProjectTree()构建,从投影树Pα中挖掘频繁项集通过Mine()实现. 为验证本文所提出方法的性能在,本实验针对误报数、产生模式数和运行时间与PUF-growth算法[12]进行对比实验.数据集选用http://fimi.Ha.ac.be/data/上的mushroom,kosarak两个真实数据集.其中mushroom是一个稠密数据集,有8124个事务,120个不同项;kosarak是一个稀疏数据集,有990002个事务,41270个不同项.在实验中对事务中的每一个数据项按照正态分布的规律随机生成一个概率值,并使该值的范围是[0,1] .对于数据集中不同的项的权重赋值同样采取上述方法. 实验算法采用C++语言实现,电脑配置为Intel(R) Xeon(R) CPU E5-1607 V3 @3.10GHz 3.00GHz的处理器,8GB内存,Microsoft Windows7操作系统.实验结果取自于多次运行的平均值,实验中的UFPM树均按照其期望支持度降序构造,频繁概率阈值τ均取值0.9. 本文所提UFPM-CM算法可以挖掘出强相关模式,但同类算法中仅仅只是挖掘不确定频繁模式,所以当和PUF-growth算法[12]作对比时,置信度阈值均设为0.同时,实验也取值验证其算法相关性挖掘效果. 120010008006004002000误报数202122232425最小支持度(%)PUFUFPMCMUFPMCMuConf06wUconf06--[ = . ,= . ]图3 mushroom数据集中误报数比较Fig.3 Number of false positives comparison for mushroom图4 kosarak数据集中误报数比较Fig.4 Number of false positives comparison for kosarak图5 mushroom数据集中运行时间比较Fig.5 Running time comparison for mushroom 实验1.误报数的比较 由于算法中使用估计值代替实际期望支持度,势必会产生一定误报.实验针对两个真实数据集进行实验,由于使用了pProxy值来计算边界值,导致了一个更紧凑的限制,所以效果如图3、图4所示,证实了UFPM-CM算法产生了更少的误报,且产生的误报数随着最小支持度的增加而减少. 实验2.运行时间的比较. 从图5、图6可以看出,UFPM-CM算法挖掘频繁项集的时间远小于PUF算法,由于其产生了更少的误报数来节省了运行时间.当给UFPM-CM算法加上两个置信度uConf和wUConf时它会预先剪枝不相关模式,因为这两个度量具有反单调性,并且值整合在了已经构造好的UFPM树和相应算法中,从而没有额外的计算量. 实验3.产生模式数的比较. 图6 kosarak数据集中运行时间比较Fig.6 Running time comparison for kosarak图7 mushroom数据集中模式数比较Fig.7 Number of patterns comparison for mushroom图8 kosarak数据集中模式数比较Fig.8 Number of patterns comparison for kosarak UFPM-CM算法与PUF算法在两个真实数据集上运行产生模式数量如图7、图8所示,图中可以看出,所产生的模式数明显减少.其中,利用UFPM树中pProxy度量值有效剪枝了非频繁项集.当使用uConf和wUConf这两个置信度时,将产生强相关的模式. 以上实验证实,UFPM-CM算法利用UFPM树高效地存储了不确定数据库,快速挖掘出较少、相关性强的频繁模式且其效率优于同类算法. 通过对不确定频繁项挖掘的研究,本文提出了新的不确定模式树UFPM-tree和对应的UFPM-CM算法.深入研究项集之间的相关性和权重度量来发现有价值的相关模式,其中引入了uConf和wUConf两个置信度来挖掘强相关模式.通过实验证明,本文所提出的算法在误报数的减少、运行时间和产生的模式数量上优于其他同类算法.未来,UFPM-CM算法将探索挖掘其他类型的数据挖掘,例如网络数据流等.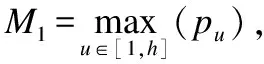
4 本文算法


5 实验与分析

6 结 论
