不确定数据频繁项集挖掘算法研究

赵学健，熊肖肖，张欣慧，孙知信

(1.南京邮电大学 现代邮政学院，江苏 南京 210003；2.南京邮电大学 物联网学院，江苏 南京 210003)

0 引 言

作为数据挖掘领域研究的重要分支之一，频繁项集挖掘的主要目的是以频繁出现的项目集的形式发掘嵌入在海量数据中的隐式的、先前未知的、潜在的有用知识[1-4]。当前，频繁项集挖掘在各领域应用广泛，如银行数据分析、市场营销、医疗诊断、气象数据分析等[5]。上述应用中广泛存在不确定数据，造成数据不确定性的原因主要有：对现实世界的有限感知和理解能力；感知监测设备的局限性；用于收集、储存、转换或数据分析的可用资源的限制；无线传输错误或网络延迟；数据粒度或隐私保护。因此，针对不确定数据的频繁项集挖掘引起了学者的广泛关注。

文中首先介绍了不确定数据的定义，并分析不确定数据频繁项集挖掘的概率模型。接着详细介绍了当前针对不确定数据的主流频繁项集挖掘算法，将主流频繁项集挖掘算法分为3类：基于候选项集生成和测试的频繁项集挖掘算法，基于模式增长的频繁项集挖掘算法和基于生物启发的频繁项集挖掘算法，分别介绍3类算法的代表性算法，并对相关算法的性能进行了简单分析。最后进行总结与展望。

1 定义及模型

在早期，最常见的频繁项集挖掘算法主要用于搜索传统的确定数据库。然而，在各种实际应用中，数据库中的每一条事务中项目的存在不是百分百确定的，而是依据某种相似性度量或是概率形式存在，比如说通过分析购物篮数据来预测商品需求量时，购物篮中的商品用户并不是肯定要购买的，而是存在一个不确定性。

在过去几年中，许多模型被提出用于不确定数据的分析[6-7]，其中概率模型受到了众多研究者的青睐。从概率模型的角度来看，在不确定数据集D中，用户可能无法确定事务Tq中是否存在某个项目集X，这种不确定性可以用存在概率p(X,Tq)来表示，p(X,Tq)表示X存在于事务Tq中的可能性。存在概率p(X,Tq)的取值最小为一个接近0的正值，表示X在D中存在的可能性不大，趋近于0；存在概率p(X,Tq)的取值最大为1，表示项目集X绝对存在。从这个意义上说，传统的确定数据库可以看作每一个项目在事务Tq中的存在概率均为100%的不确定数据库。不确定数据的概率模型涉及以下三个定义。

定义1(项集在事务中的存在概率)：项集X在事务Tq中的出现概率记为p(X,Tq)，等于项集中各项目在事务Tq中存在概率的乘积。

即：

其中，Ij为项集X的第j个项目。

定义2(项集的期望支持度)：项集X在不确定数据库D中的期望支持度记为expSup(X)，等于项集X在包含该项集的所有事务中的出现概率之和。

即：

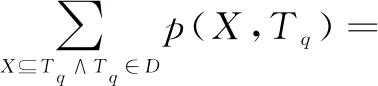
定义3(频繁项集)：在不确定数据库D中，当项集X的期望支持度大于等于最小期望支持度时(最小期望支持度为最小期望支持度阈值δ与数据库D中所包含事务数的乘积)，则项集X为频繁项集，即当expSup(X)≥δ×|D|时，项集X为频繁项集。

2 频繁项集挖掘算法

2.1 基于候选项集生成和测试的频繁项集挖掘算法

从不确定数据中挖掘频繁项集的一种重要方法是首先生成候选频繁项集然后扫描数据库对候选频繁项集进行测试。基于这个思想，Chui等[8]提出了U-Apriori算法，该算法从不确定数据中挖掘频繁模式的方法是分层的、宽度优先的、自下而上的。具体来说，U-Apriori算法首先计算所有1-项集的期望支持度，通过扫描不确定数据库，那些期望支持度大于最小期望支持度的项目最终组成频繁1项集。然后，U-Apriori算法反复应用候选项集生成和测试的过程，从频繁k项集生成候选k+1项集，并测试它们是否是频繁的k+1项集。U-Apriori算法与用于挖掘确定数据的Apriori算法[2]是一样的，都依赖于Apriori属性，即频繁模式的所有子集也必须是频繁的，反之任何非频繁项集的所有超集也是非频繁项集，该性质也称为向下闭包特性。

U-Apriori算法还通过采用LGS-修整策略来提高其效率，LGS-修整包括局部修整、全局剪枝和单次修补。

该策略从不确定数据的原始概率数据集D中剔除每一项存在概率低于用户指定的修剪阈值的项，然后从修剪以后的数据集中挖掘频繁项集。

Chui等[9]采用递减修剪技术，进一步提高了U-Apriori的效率。递减修剪技术通过估计候选频繁项集的期望支持度的上限以减少候选模式的数量。如果候选频繁项集X的估计期望支持度上限值低于最小期望支持度，则立即剪除该候选频繁项集X。

2.2 基于模式增长的频繁项集挖掘算法

基于模式增长的频繁项集挖掘算法是基于候选项集生成和测试的频繁项集挖掘方法的一种有效替代方法，能够避免产生大量的候选项集。常用的模式增长频繁项集挖掘算法又可以分为两类：基于超链接结构的频繁项集挖掘算法和基于树结构的频繁项集挖掘算法。

(1)基于超链接结构的频繁项集挖掘算法。

基于超链接结构的频繁项集挖掘算法以超链接结构存储数据集的内容，在这类算法中，频繁的模式以深度优先、分而治之的方式被挖掘出来。

Aggarwal等[10]提出了一种基于超链接结构的UH-mine算法，用于从不确定数据中挖掘频繁项集。该算法用一个名为UH-struct的超链接结构存储不确定数据集D中的概率数据内容。UH-struct中的每一行表示不确定数据集D中的一个事务，与用于挖掘确定性数据的H-struct不同的是，UH-struct还存储了项目的存在概率。换句话说，对于存在于事务中的每个项目，通过UH-struct可以得到：项目本身；项目的存在概率；项目的超链接结构。因此，在UH-mine算法中，通过建立的UH-struct可以递归地扩展每个频繁项集并调整其在UH-struct中的超链接来实现频繁项集的挖掘。

该算法在较小的数据集上可以获得较好的效果，然而在大数据集上，由于H-struct需要较多的空间来存储数据集，并且算法需要多次递归调用，因此时间效率并不理想。

(2)基于树结构的频繁项集挖掘算法。

基于候选项集生成和测试的频繁项集挖掘算法使用了分层的自下而上的广度优先挖掘范式，但是往往生成的候选项集数量过多。基于超级链接结构的频繁项集挖掘算法通过递归地调整超链接结构，以深度优先的方式从不确定的数据中找到频繁的模式，时间效率也不理想。

基于树的频繁项集挖掘算法使用树结构对不确定数据集进行存储，并采用深度优先、分而治之的方法挖掘频繁项集，既可避免产生许多候选项集，又避免了递归地调整多个超链接结构，具有较好的性能。

Leung等提出了一种基于树的频繁项集挖掘算法UF-Growth[11]，类似于用于挖掘确定性数据的频繁项集挖掘算法FP-Growth[12]，UF-Growth也是通过构造一个树结构来存储数据集的内容。但是，它不使用FP-tree，因为FP-tree中的每个节点都只能记录项目及其在树路径中的出现数目。当挖掘确定性数据集时，项集X的期望支持度取决于项集X中各项目的出现次数。然而，在挖掘不确定数据时，X的期望支持度是X中各项目的发生计数和存在概率的乘积之和。因此，UF-Growth算法采用了不同于FP-tree的树结构UF-tree。

UF-tree中的每个节点由三个部分组成：项目、存在概率、项目在路径中的出现次数。UF-tree的构造方式与FP-tree的构造类似，但是只有当事务和子节点中存在相同的项和相同的存在概率时，新事务才会与子节点合并。因此，UF-tree比原来的FP-tree具有更低的压缩比。

Aggarwal等[13]提出了UFP-growth算法，与UF-growth算法一样，UFP-growth算法也会通过两次扫描不确定数据集来建立UFP-tree。UFP-tree中，当项集X对应的节点具有相似的存在概率值时，会聚集成一个超级节点。超级节点将会存储项集X、存在概率值及其出现数信息。UFP-growth算法在第二次扫描不确定数据集时才能发现所有真正频繁的模式，然而由于UFP-growth的近似性质，UFP-growth算法除了能够发现那些真正频繁的项集之外，还会发现一些不常见的模式，称为假阳性模式。

因此，需要对不确定数据集进行第三次扫描，以消除这些错误。

Leung和Tanbeer[14]提出了一种用于不确定数据集的频繁项集挖掘算法，称为CUF-growth算法。该算法构建了一种叫做CUF-tree的树结构，与UFP-growth算法一样，CUF-growth算法也对不确定数据集进行三次扫描，以挖掘频繁项集。CUF-growth首先扫描数据集以计算事务上限，然后通过第二次扫描数据集构建CUF-tree。在第二次扫描不确定数据集结束时，CUF-growth算法会发现所有潜在的频繁项集。由于这些潜在的频繁项集包括所有真正频繁的项集和一些并不频繁的项集，CUF-growth算法最后通过第三次快速扫描数据集，以检查每个项目集，验证它们是否是真正频繁的，即修剪假阳性项目集。

Leung和Tanbeer[15]引入了前缀项上限的概念，并提出了相应的PUF-growth算法用于挖掘不确定数据集中的频繁项集。与UFP-growth和CUF-growth一样，PUF-growth算法也对不确定数据的概率数据集进行三次扫描，以挖掘频繁项集。在第一次扫描中，PUF-growth计算前缀项上限。在第二次扫描中，PUF-growth构建PUF-tree。PUF-growth算法也是在第二次扫描不确定数据集结束时找到所有潜在频繁项集。因为这些潜在的频繁项集包括所有真正频繁的项集和一些罕见的项集。PUF-growth算法最后通过第三次快速扫描数据集，检查每个数据集是否真的频繁。PUF-growth算法采用的前缀项上限与CUF-tree算法的事务上限相比更加接近项集的期望支持度，因此在第三次扫描过程中，需要检验的假阳性项目集数量通常小于CUF-growth算法需要检验的项目集数量，速度更快。

2.3 基于生物启发的频繁项集挖掘算法

上述基于候选项集生成与测试的频繁项集挖掘算法以及基于模式增长的频繁项集挖掘算法都是精确挖掘算法，也就是说这些算法都可以挖掘出数据集中的所有频繁项集。这类算法虽然精确度高，但是时间复杂度通常与数据集的规模成正比。当数据集非常大时，比如社交网络数据[16]或者大型生物信息数据集[17]，精确的频繁项集挖掘算法几乎是无能为力的[18]。

为了解决精确频繁项集挖掘算法时间效率低下的问题，研究人员提出了基于生物启发的频繁项集挖掘算法，比如基于遗传算法的频繁项集挖掘算法[19-20]，基于群体智能的频繁项集挖掘算法等[21]。基于生物启发的频繁项集挖掘算法可以在规定的合理时限内完成，但是通常该类算法不能挖掘出所有的频繁项集，称之为模糊频繁项集挖掘算法。因此，针对大型的不确定数据集，提出合适的生物启发频繁项集挖掘算法在保证时间效率的前提下获得更高质量的频繁项集，将会是一个持续的挑战。

文献[19]提出的GA-FIM算法将每一个项目集看成由n个元素组成的向量，如果该项目集的第i个元素属于该项目集，则将向量的第i个元素设置为1，否则设置为0。比如说数据集中包含5个项目，即I={a,b,c,d,e}，则项目集bde可以用向量{0,1,0,1,1}表示。接下来，在完成初始化后将执行遗传算法的交叉、变异和选择操作，直到达到预先设置的轮数为止。最终，GA-FIM算法得到的频繁项集为每一轮过程中发现的频繁项集的集合。

文献[21]最早提出了PSO-FIM算法，文献[22]后期又对PSO-FIM算法进行了改进。在PSO-FIM算法中，群体中的每一个粒子代表一个项目集，粒子在初始化时随机设置为项目集空间中的任意一个项目集。PSO-FIM算法初始化时首先构造一群随机粒子，接下来通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个极值来进行更新，第一个值是本粒子找到的最优解，即具有最大期望支持度的项目集，第二个值是整个粒子群找到的最优解。

文献[19]和文献[21]表明，GA-FIM算法和PSO-FIM算法相对于当前的精确频繁项集挖掘算法具有更好的时间效率。然而，这两种算法所得到的频繁项目集结果并不理想，也就是说算法的最终输出仅为频繁项目集的一个子集。

3 算法性能对比分析

上述对不确定数据集的频繁项目集挖掘算法进行了分类划分，并对代表性算法进行了介绍，包括U-Apriori、UH-mine、UF-growth、UFP-growth、CUF-growth、PUF-growth、GA-FIM及PSO-FIM等。

在准确性方面，U-Apriori、UH-mine、UF-growth、UFP-growth、CUF-growth、PUF-growth算法都可以返回满足用户指定最小期望支持度阈值的所有频繁项集。然而，GA-FIM及PSO-FIM算法由于融合了启发式智能算法的思想，不一定能够返回所有符合条件的频繁项目集，准确性相对较差。

在内存消耗方面，U-Apriori保留了候选频繁项集列表，而基于树和超链接结构的算法则构造内存结构，比如UF-tree及其变体，扩展的H-struct等。一方面，UF-tree比扩展的H-struct更紧凑，即需要更少的空间。然而，另一方面，UH-mine只保留一个扩展的H-struct，而基于树的算法通常构造不止一棵树，树的大小也可能不同。

因此，基于树和超链接结构的算法的内存消耗要根据具体算法和数据集情况来确定。GA-FIM及PSO-FIM算法不需要保存大量候选频繁项集或其他内存结构，内存消耗较小。

就时间性能而言，GA-FIM及PSO-FIM等基于生物启发的频繁项集挖掘算法可以灵活设置，通常优于其他几种算法。

基于候选项集生成和测试及基于模式增长的频繁项集挖掘算法的时间性能影响因素较多。首先，项目对应的存在概率会影响算法的时间性能。通常不确定数据集中的项目呈现较低的存在概率时，大多数算法的性能都很好，因为这些数据集不会导致较长的频繁模式。当项目呈现较高的存在概率值时，U-Apriori算法会生成更多的候选频繁项集，U-growth算法需要构造更多更大的UF-tree，UH-mine算法需要调整更多的超链接结构，自然都需要更长的运行时间。其次，当最小期望支持度减小时，往往会得到更多的频繁项目集，当然也需要更长的运行时间。此外，数据集的密度也会影响运行时间。例如，当数据集密集时，UF-tree获得了更高的压缩比，因此与稀疏数据集相比，遍历所需的时间更短，时间性能更好。

4 结束语

频繁项集挖掘是一项重要的数据挖掘任务，有助于发现隐式的、先前未知的潜在有用的知识，有助于揭示许多现实生活应用中共同发生的项目。由于许多现实生活应用中的数据都具有不确定性，因此，近年来不确定数据的频繁项集成为研究者们关注的焦点。文中介绍了不确定数据频繁项集挖掘算法的相关成果，其中包括基于候选项集生成和测试的、基于模式增长的以及基于生物启发的频繁项集挖掘算法，并对典型代表性算法进行了介绍，对其性能进行了分析。

未来的可能研究方向包括：(1)基于生物启发的频繁项集挖掘算法的改进创新；(2)在社交网络分析等应用领域的不确定数据中挖掘频繁项集；(3)从不确定数据中挖掘频繁序列和频繁图；(4)不确定频繁模式的可视化分析。