基于共现结构的频繁高效用项集挖掘算法
2022-04-26杨海军张博岚路永华
杨海军,张博岚,路永华
(兰州财经大学 信息工程学院,甘肃 兰州 730020)
0 引言
模式挖掘多年来一直是数据挖掘研究领域的重要课题,主要内容包括频繁项集挖掘、高效用项集挖掘、序列挖掘等.频繁项集指的是在数据库中的支持度不低于用户指定的最小支持度阈值的项集.频繁项集挖掘算法[1-5]的意义在于发现数据库中大量出现的项集,其主要可分为2大类:基于水平层级机制和基于模式增长机制,前者以Apriori算法[1]为代表,后者以FP-Growth算法[2]为代表.在实际应用中,频繁项集挖掘算法基于所有项都具有相同“利润”的假设是不能完全满足实际需求的,因此高效用项集的概念和模型在文献[6]中开始被提出,并在同年发表的文献[7]中通过TWDC(Transaction Weighted Download Closure)策略得到解决.高效用项集指的是数据库中效用值不小于用户设定的最小效用阈值的项集.一般的高效用项集挖掘算法[8-14]通过应用效用模型(包括商品利润、物品重要性、用户偏好程度等)发现数据库中的所有高效用项集.但随着频繁项集挖掘算法和高效用项集挖掘算法的大量涌现和应用,研究人员发现单独使用频繁项集挖掘或高效用项集挖掘方法在实际应用中存在一定局限性,比如一些出现频率很高的商品及商品组合能够给商家提供的利润是很小的,例如食盐;而一些效用很高的商品,出现频率却很低,例如奢侈品,会使得相应频繁项集或高效用项集的出现具有一定的偶然性.因此,发现既频繁又高效用的项集具有重要的理论意义和实践价值.
近两年新颖的模式挖掘算法越来越多地被提出,如Min等[15]通过将字母分为强、中、弱3个部分,提出了3支挖掘算法,并在3种数据集上验证了该算法对于生物数据、时间序列数据和文本数据的灵活性和适用性.Dong等[16]以负序列为研究对象提出了top-k NSP(top-k Negative Sequential Pattern)算法,并针对有用负序列的挖掘方法和减少时间消耗问题提出了2个解决策略.Wu等[17]为了减少无用项集的产生,基于网状树结构提出了NetNCSP(Nettree for Nonoverlapping Closed Sequential Pattern)挖掘算法,对闭序列模式和无重叠序列模式挖掘都有较好的效果.
本文提出频繁高效用项集挖掘算法(improved FHM with Support,iFHMS),该算法是基于传统高效用项集挖掘算法(Fast High-Utility Miner,FHM)的拓展,通过构建1个改进的共现结构,实现数据库中频繁高效用项集的挖掘.
1 基本知识
数据库D由1组事务Tj(j=1,2,…,m)组成,即D={T1,T2,…,Tm},每个Tj都是1个项集I,由n个项构成,即D={i1,i2,…,in},项的个数为k的项集被称为k-项集.D中的每条事务Tj都有且仅有1个事务标识符,记作TID.
表1展示的是1个数据库实例,它包含5条事务(T1,T2,T3,T4,T5)和7个不同的项(a,b,c,d,e,f,g),每个项都有1个内部效用iu(ip,Tj)和外部效用eu(ip),分别为表1中括号内的数字和表2中的Profit行中的数值.

表1 数据库实例

表2 项的外部效用
定义1项ip在事务Tj中的效用u(ip,Tj),表示为
u(ip,Tj)=iu(ip,Tj)× eu(ip)
(1)
例如,项a在T1中的效用U(a,T1)=1×5=5.
定义2项集X在事务Tj中的效用U(X,Tj),表示为
(2)
例如,项集{ac}在T1中的效用U({ac},T1)=1×5+1×1=6.
定义3项集X在数据库D中的效用U(X),表示为
(3)
例如,项集{ac}的效用U({ac})=(1×5+1×1)+(2×5+6×1)+(1×5+1×1)=28.
定义4事务Tj的效用TU(Tj),表示为
(4)
例如,T4的效用TU(T4)=4×2+3×1+3×2+1×3=20.
定义5项集X的事务加权效用TWU(X),表示为
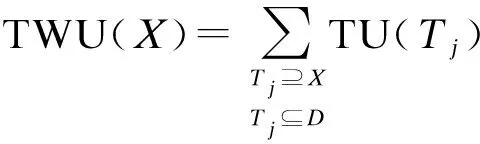
(5)
例如,项集{ac}的事务加权效用TWU({ac})=TU(T1)+ TU(T2)+ TU(T3)=65.
性质1事务加权向下闭包属性.对于用户设定的最小效用阈值mutil,若有TWU(X) 例如,项集{ac}的支持度计数Sup({ac})=3. 定义7项集X在事务Tj中的剩余效用RU(X,Tj).项集X⊆Tj,数据库中的所有项按顺序≻排列,排在X之后的所有项的集合被记为Tj/X,则RU(X,Tj)为集合Tj/X的效用值[2],即 (6) 例如,假设≻为字典序,有a≻b≻c≻d≻e≻f≻g,则项集{bd}在T3中的剩余效用为[3] RU({bd},T3)=u(e,T3)+u(f,T3)=3 + 5=8. 性质2支持度向下闭包属性.假设用户设定的最小支持度阈值minSup,若有Sup(X)≥ minSup,则项集X及其所有非空子集均为频繁项集;反之,项集X及其所有超集都不是频繁项集. 问题定义:频繁高效用项集挖掘算法的目的是发现数据库中所有效用不小于最小效用阈值并且支持度不小于最小效用阈值的项集[4],即 FHUIs={X:Sup(X):U(X)|X⊆I,Sup(X)≥ minSup,U(X)≥ mutil}. 例如,当mutil=40,minSup=2时,数据库D的FHUIs={dbec}. 本文提出的iFHMS算法构建了1个新的数据结构——USCS(Utility and Support Co-occurrence Structure),其对FHM算法中构建的EUCS(Estimated Utility Co-occurrence Structure)做出了2方面的改进.一方面,USCS在原EUCS的基础上新增了支持度的存储;另一方面,USCS不再存储不满足效用约束或支持度约束的相应2-项集的TWU和支持度. 若对表1设定mutil=40,minSup=2,则iFHMS算法构建的USCS见表3. 由于iFHMS算法是在FHM算法的基础上加上了支持度约束,其搜索空间和存储结构均与FHM算法相同,参考文献[11]即可,只是在效用列表中新增了1项支持度计数的统计信息,通过统计效用列表的TID的总数获得. 策略1Item剪枝.对于1-项集X,若有TWU(X) 策略2CS剪枝.对于2-项集X,若在USCS中,存在TWU(X) 策略3SU剪枝.对于k-项集X(k≥ 3),若有∑(iutil+rutil) 实际上,以上3种剪枝策略都是在效用约束条件的基础上加入支持度约束条件,只要2个条件中有1个不能满足,就可认定该项集及其所有的扩展项集一定不是频繁高效用项集. 对于策略1和策略2,根据已有的众多经典频繁项集挖掘算法和高效用挖掘算法,已经充分论证了TWU向下闭包属性和支持度向下闭包属性,而从USCS结构的存储原则来看,所有TWU或支持度的值小于最小效用阈值或最小支持度阈值的项都已被剔除,被剔除项组成的2-项集一定不满足TWU和支持度向下闭包属性,所以包含被剔除2-项集的任意超集都不可能是频繁高效用项集. 对于策略3,假设项集X的超集为X′,则有[5] 所以如果存在U(X)+ RU(X) 综上,USCS结构以及3个剪枝策略对于频繁高效用项集挖掘是有效的. iFHMS算法同样需通过构建效用列表结构,并对其进行连接来实现频繁高效用项集的挖掘过程,根据策略1构建的初始效用列表见图1. 图1 初始效用列表 根据策略3,只对1-项集{d}有∑(iutil+rutil)=53>40,即有且仅有项d的扩展项集中可能存在频繁高效用项集,故根据策略2构建2-项集的效用列表,见图2. 根据策略3,只有{db}的扩展项集中可能存在频繁高效用项集,故构建的3-项集的效用列表如图3所示. 根据策略3,只有{dbe}的扩展项集中可能存在频繁高效用项集,故构建的4-项集的效用列表如图4所示. 图2 2-项集效用列表 图3 3-项集效用列表 图4 4-项集效用列表 挖掘过程结束,FHUIs={dbec}. iFHMS算法的实现过程见 Algorithm 1.算法以用户数据库D、设定最小支持度阈值minSup和最小效用阈值mutil为输入值.算法首先对数据库D进行2次扫描,第1次扫描计算出所有项的支持度和事务加权效用TWU;第2次扫描时根据策略 1 将Sup Algorithm 1 iFHMS算法输入:事务数据库D;最小支持度minSup;最小效用阈值mutil输出:频繁高效用项集FHUIs1.扫描数据库D,计算所有项的Sup和TWU;2.若有Sup(i)≥minSup且TWU(i)≥mutil,则项i∈I∗;3.按I∗中元素的TWU升序,排列数据库中的事务;4.扫描更新后的数据库D,构建共现结构和效用列表;5.Search(Ø,I∗,mutil,minSup,USCS).2-项集及k-项集(k≥3)效用列表的构建过程及高效用项集挖掘过程分别是Algorithm 2和Algorithm 3.Algorithm 2 Search过程(挖掘过程)输入:P.UL:项集P的效用列表;Px.UL:项集P的扩展项集Px的效用列表;mutil:最小效用阈值;minSup:最小支持度;USCS:共现结构;输出:频繁高效用项集FHUIs1.for each Px do if SUM(Px.UL.iutil)≥mutil and Sup(Px)≥minSup then2. OUTPUT Px;3. end if SUM(Px.UL.iutil)+SUM(Px.UL.rutil)≥mutil and Sup(Px)≥minSup then6. exULs=NULL;7. for each Py(y>x)do8. if ∃(x,y,c,s)∈USCS 且c≥mutil and s≥minSup then9. Pxy←Px∪Py;10. Pxy.UL←Construct(P,Px,Py);11. Ext(Px)←Ext(Px∪Py);12. end13. end14. Search(Px,Ext(Px),minutil,minSup,USCS);15. end16.end Algorithm 3 Construct过程(效用列表构建过程)输入:P.UL:项集P的效用列表;Px.UL:项集Px的效用列表;Py.UL:项集Py的效用列表(x∈E(P),y∈E(P))输出:Pxy.UL:项集Pxy的效用列表1.Pxy.UL=NULL;2.foreach ex∈Px.UL do;3.if ∃ ey∈Py.UL and ex.tid=ey.TID then4. if P.UL≠NULL then5. 查找所有满足条件e.TID=ex.TID的元素e,e∈P.UL;6. exy= 为验证本文提出的iFHMS算法中做出的2个改进之处是否有效,实验将该算法与SFHM(Fast High-Utility Mining with Support)算法进行了对比,其中,SFHM算法是在FHM[11]算法中增加存储2-项集支持度的结构ESCS(Estimated Support of Co-occurrence Structure)的变体.实验环境:硬件:4G内存惠普台式电脑;软件:Ubuntu、Java、Maven. 实验使用的数据集均是从SPMF(见网页http://www.philippe-fournier-viger.com/spmf/.)公开资源库中下载的标准数据集,见表4.数据集Retail是消费记录数据,包含了真实的外部效用和内部效用,采用对数正态分布分别在[1,1 000]和[1,5]之间随机产生数据集Accident和Mushroom的外部效用和内部效用. 表4 数据集特性 实验结果表明,iFHMS算法在内存占用方面基本无改善,故这里不再讨论. 为研究最小效用阈值对iFHMS算法挖掘时间效率的影响,实验需保持每个数据集的最小支持阈值不变,3个数据集上的最小支持度阈值minSup分别设为40%、10%、0.05%.iFHMS算法的挖掘时间t随最小效用阈值变化情况如图5所示. 从图中可以看出,在不同数据集上,iFHMS算法的挖掘时间随最小效用阈值的增大而逐渐减小,这说明该算法是可行的.同时,iFHMS算法的时间效率相比对比算法有一定程度的提升,在3个不同数据集上的平均减少幅度分别为6.69%、7.43%、4.05%. 图5 不同mutil下算法时间对比 为探讨最小支持度阈值对iFHMS算法挖掘时间效率的影响,实验需在保持每个数据集的最小效用阈值不变的情况下进行,3个数据集上的最小效用阈值mutil分别设为3×106、1×105、200[7].iFHMS算法的挖掘时间t随最小支持度阈值变化情况如图6所示. 图6 不同minSup下算法时间对比 从图中可以看到,iFHMS算法的挖掘时间都随最小支持度阈值的增大而减少,这说明该算法对于挖掘频繁高效用项集是可行的.并且iFHMS算法的时间效率是有一定程度的提升的,在3个数据集上的平均提升幅度分别为2.88%、3.01%、2.36%. 与SFHM算法相比,iFHMS算法在空间和时间上都能一定程度地减少消耗.因为利用USCS可以同时对2-项集的TWU和支持度计数进行计算,iFHMS算法一旦发现某个值小于其阈值,就进行下一个项集的计算和判断,从而避免了需对某些2-项集的TWU和支持度都构建存储结构并进行计算的可能.比如,在对数据库D进行挖掘的整个过程中,当判断了只有{d}的扩展项集中存在频繁高效用项集时,iFHMS算法通过USCS结构就能直接知道,只需构建2-项集{db}、{de}、{dc}的效用列表.但SFHM算法就必须分别计算{da}、{db}、{dc}、{de}的EUCS和ESCS,并与mutil和minSup比较,才能确定有希望的频繁高效用2-项集.这就是iFHM算法优于SFHM算法的原因所在. 考虑到频繁高效用项集在实际生活中的应用价值,本文通过构建一个改进的共现结构USCS,并提出基于此结构的iFHMS算法实现频繁高效用项集挖掘.iFHMS算法将EUCS和ESCS结构进行合并形成USCS,其优势主要体现在2-项集效用列表的构建过程中能够减少没有希望的2-项集的效用列表.最后通过对比实验说明,iFHMS算法能够有效发现数据库中的频繁高效用项集,且在时间效率方面有一定程度的提升.后续也会针对剪枝策略进行改进,以进一步提高算法效率.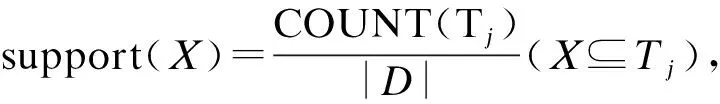
2 iFHMS算法
2.1 剪枝策略
2.2 效用列表的构建
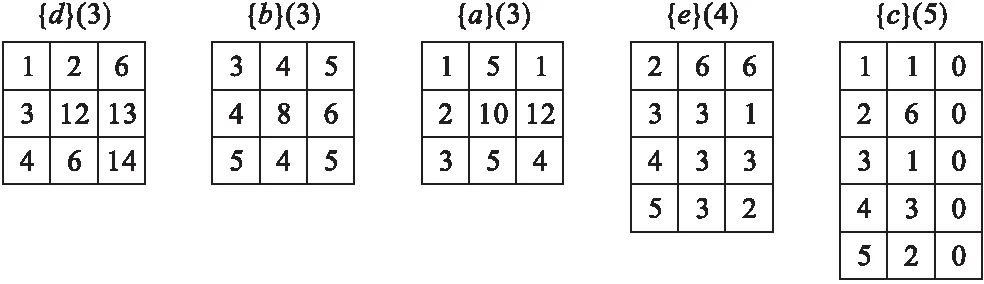

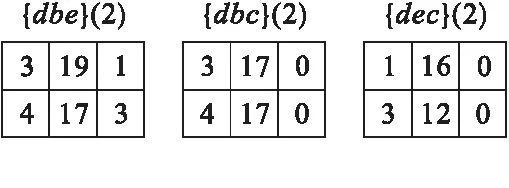
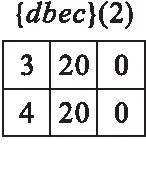
2.3 算法流程介绍


3 实验及结果分析

3.1 最小效用阈值对时间效率的影响

3.2 最小支持度阈值对时间效率的影响

3.3 结果分析
4 结论
