一种共轴双旋翼飞行器悬停控制联合仿真

陈汉， 李科伟， 邓宏彬， 危怡然， 赵瑾

(1.北京理工大学 机电学院, 北京 100081; 2.中国兵器工业集团有限公司 第203研究所, 陕西 西安 710065)

0 引言

无人机近年来受到越来越多科学家及工程师的关注，尤其是微小型无人机。微型旋翼机比全尺寸直升机更灵活，其尺寸紧凑的特点以及悬停、转弯和向各方向移动的能力使小型旋翼航空器非常适合动态环境下的操作。与固定翼飞机相比，微型旋翼飞机具有显著优势，特别是在需要保留飞机静止(悬停)时或在严格受限的环境中操纵。在战场环境中，微型旋翼无人机可以执行多种任务，例如侦查环境、电子对抗、通讯中继甚至直接攻击目标等[1]。

由于可操作性、多功能性、稳定性和易于控制等优势，再考虑到实际的工程项目需求，飞行器能够携带质量较大的任务载荷，本文选择微型共轴旋翼机而不是单旋翼的配置方案。与目前最流行的四旋翼飞行器对比，共轴双旋翼飞行器的结构更加紧凑，尽管目前存在一些可折叠四旋翼飞行器，但四旋翼飞行器无法满足折叠后的尺寸要求，而本文所涉及的共轴双旋翼飞行器其翼片折叠后特征尺寸显著减小，更加便携，适合放置在狭长的火箭弹舱室内运输并投放，且折叠旋翼比折叠机身结构设计更简单可靠，因此本文采用共轴双旋翼的配置方案[2]。

然而，四旋翼飞行器的相关控制算法相比之下更加简单，研究已经非常成熟，而共轴双旋翼飞行器的相关研究则较少，尤其是国内关于微小型共轴双旋翼飞行器控制算法的文献几乎没有。目前，国外相关的研究工作有：美国Drexel大学Husnic[1]对一种微型共轴双旋翼直升机设计了控制器，并利用MATLAB/Flightgear进行了联合仿真；Maryland大学Lee[3]对双旋翼涵道飞行器的悬停和前进飞行性能进行了研究；Duke大学Giovanetti[4]对共轴双旋翼的最小功率控制和转子优化设计进行了研究；Purdue大学Arama[5]对一种小型共轴双旋翼飞机设计了混合控制策略，在仿真中得到了较好的结果。另外Gecgel[6]、孙茂等[7]、Wicha[8]在共轴双旋翼的空气动力特性和优化功率损耗方面均做出了独立研究。国内的相关研究工作有：南京航空航天大学宁承威[9]对共轴倾转旋翼机的飞行动力学建模与控制进行了研究；北京理工大学黄祥斌[10]对一种采用空气舵控制的球形共轴旋翼飞行器进行了总体设计，包括控制算法和飞行实验；清华大学袁夏明等[11-12]对共轴式无人直升机建模与鲁棒跟踪控制进行了深入细致的研究，完善了相关理论；石征锦等[13]对Fuzzy-PID算法在共轴双旋翼姿态控制的应用进行了研究；匡银虎等[14]研究了模糊自适应算法在多旋翼飞行器控制中的应用；李悦[15]对共轴双旋翼涵道飞行器的气动特性和仿真方法进行了独立研究。

从控制器设计和仿真技术来看，国内外相关研究普遍基于对共轴双旋翼的简化或近似的动力学模型对控制算法进行设计，并在MATLAB/Simulink仿真平台上对控制算法进行性能测试。这种做法存在两方面问题：首先，只能依靠经验公式和近似理论求解上旋翼和下旋翼干扰的问题，在样机测试之前无法准确判断不同系统状态下的升力大小和方向，模型仍存在系统误差。如果控制器对模型的依赖较强，即使在仿真中可能取得较好的成果，在样机实验中也会因为未建模的误差、装配和加工精度、舵机精度等问题造成姿态发散。其次，MATLAB中难以对飞行器的复杂操纵机构进行准确建模，目前仿真方法使用的都是简化数学模型，将其整体考虑为一个刚体加上外部控制力的方式，忽略了机体上各部件的相对运动。显然这种做法是不准确的，没有建立起舵机动作量和控制算法输出控制量之间的联系，控制器输出量和实际情况差距很大。

基于以上现状，本文主要在以下两方面实现了创新：第一，采用适应性和鲁棒性更好的滑模控制算法，应用于控制执行机构复杂的共轴反桨式无人机上，使姿态控制更加迅速稳定；第二，将Adams/MATLAB联合仿真技术应用于飞行器控制仿真，解决具有复杂操纵机构的无人机难以进行数学建模和数值仿真的问题，利用联合仿真技术，较好地对实际飞行器动力学系统包括舵机及其传动机构进行建模，可信度更高[16]。从而使得本文设计的悬停控制算法具备可靠性和有效性，并具有可视化的优点，通过动画保存可以直观地找出设计中的错误，成果展示的效果也更好。

1 飞行器操纵原理

本文所涉及的共轴双旋翼飞行器由任务载荷、电池仓、机身、下桨盘、上桨盘等5大部分组成，所有结构的三维建模均在Solidworks 2018软件中完成，如图1和图2所示。

图1 翼片折叠后Fig.1 Folded wings

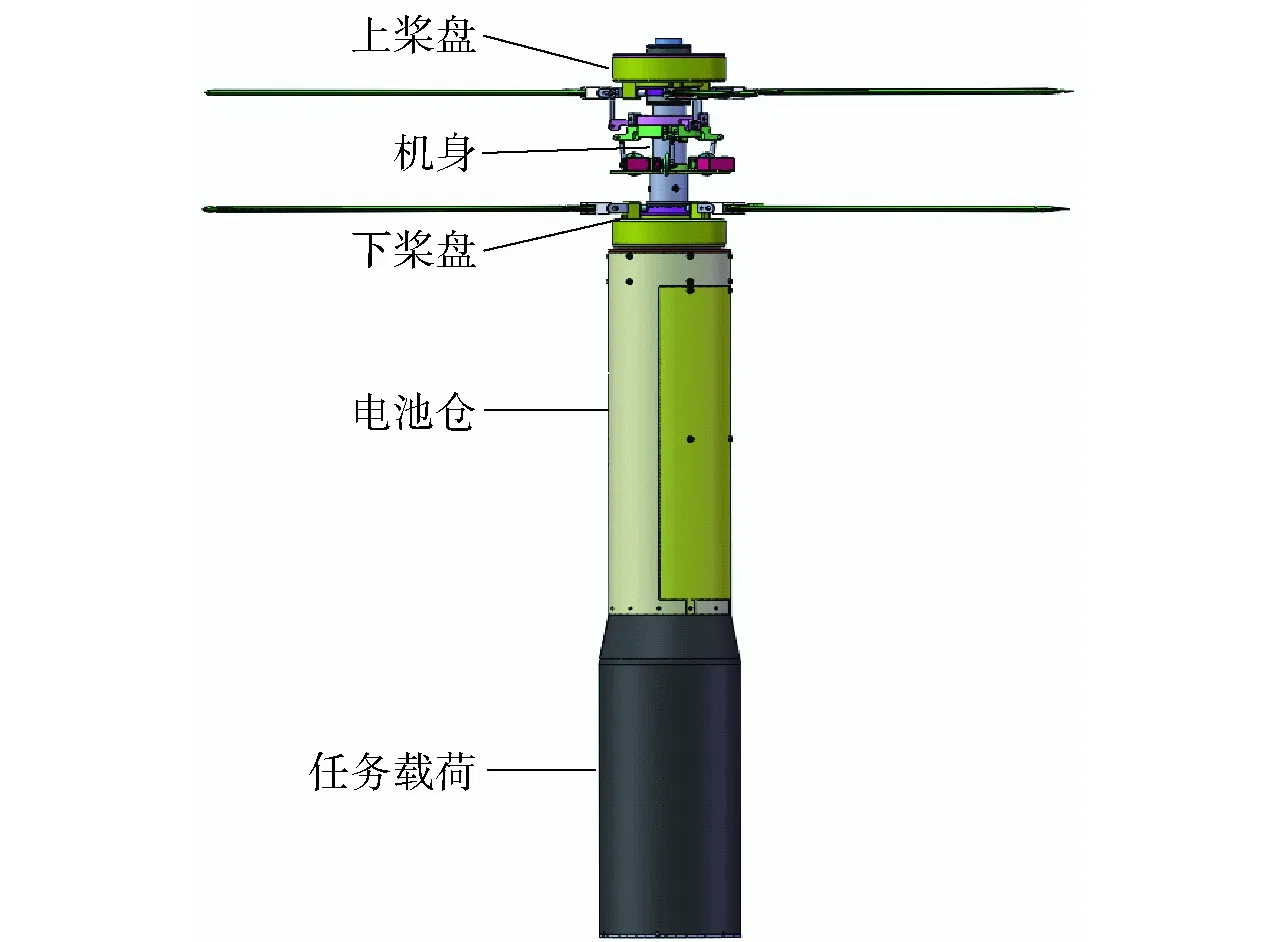
图2 共轴双旋翼飞行器结构组成Fig.2 Structure of coaxial dual-rotor aircraft

由图2可知，飞行器电池仓和任务载荷都可以看作是飞行器载荷，它们与机体固连；上桨盘和下桨盘的桨叶均可折叠，飞行时通过离心力展开并达到水平位置，桨叶与桨盘铰接副的活动范围为90°. 下面介绍机身上舵机控制航向的方式，操纵机构如图3所示。

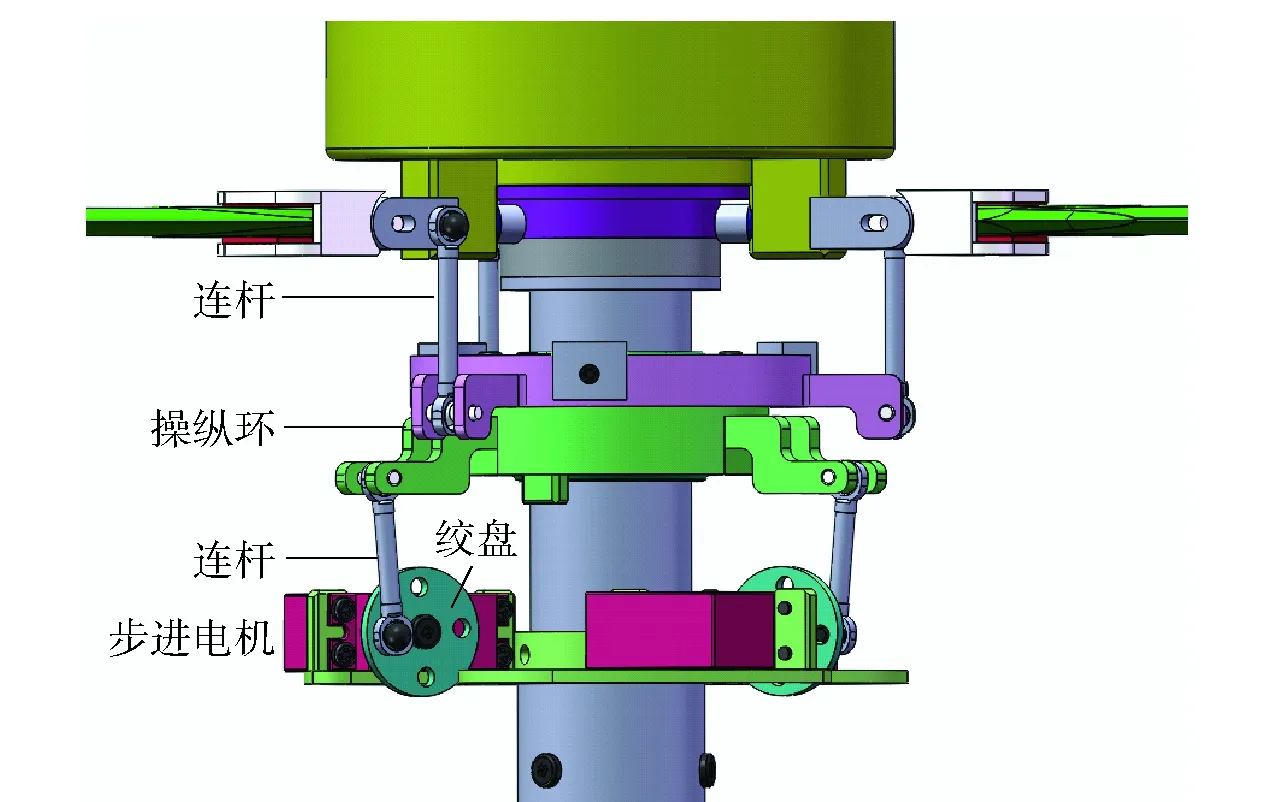
图3 操纵机构Fig.3 Control mechanism

图3中所有的连杆两端均为球铰约束，由步进电机带动绞盘和连杆，与上方的操纵环连接，操纵环内是1个球面轴承，使操纵环中心点与飞行器中心轴线重合，但是可以倾斜及沿轴线上下运动。根据几何知识，空间中的3个点可以确定1个平面，因此操纵环的位置和姿态可以通过3个舵机完全确定。当操纵环平面法向量不与机身中心轴线重合时，上桨叶迎角是周期性变化的，桨叶在转动过程中在连杆带动下其迎角与下方操纵环的姿态对应，在操纵环较高处桨叶的迎角也会变大，从而使产生的升力变大，在操纵环较低的位置则相反。最后的效果就是上桨盘所产生的所有桨叶升力合力方向与操纵环平面的法向量方向完全一致。

当飞行器向前飞行时，桨叶开始挥舞运动，这种运动较为复杂，会给控制器设计带来挑战。本文所涉及的飞行器在结构设计上限制了挥舞运动的幅度、减轻了其影响，并在动力学建模中考虑了挥舞运动带来的周期性变距问题，采用近似方法对其进行建模，同时采用滑模控制解决建模不精确问题[17]。

2 飞行器动力学模型

2.1 无上旋翼和下旋翼干扰及挥舞运动的模型

为建模方便，现引入2个坐标系，即大地坐标系OXYZ和机体坐标系oxyz. 其中OXYZ坐标系可视为惯性坐标系，oxyz坐标系为机体坐标系，且oxyz的原点位于飞行器质心位置。飞行器坐标系以及简化模型如图4所示。

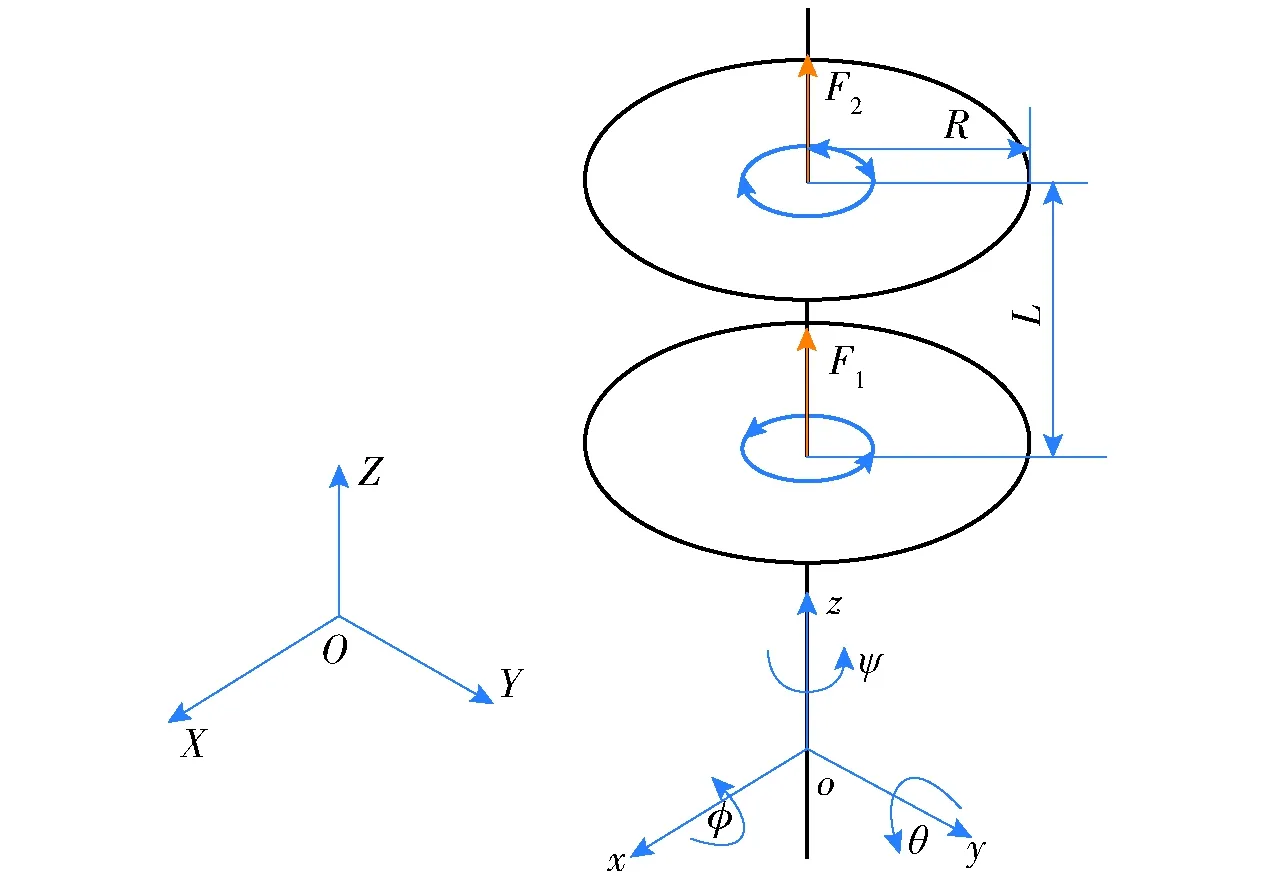
图4 飞行器坐标系以及简化模型Fig.4 Aircraft coordinate system and simplified model

图4中，φ、θ、ψ表示欧拉角，即分别为滚转角、俯仰角和偏航角，F1、F2分别为下旋翼和上旋翼的升力，R为桨盘半径，L为上旋翼到下旋翼安装中心的距离。

为了便于分析，在确保研究结果有效的前提下，本文提出以下3点假设：

1)将整个共轴双旋翼飞行器视作1个刚体；

2)将共轴双旋翼飞行器质心与中心对称轴视作重合；

3)由于旋翼体积和质量很小，可忽略旋翼陀螺效应对系统动力学特性的影响[18]。

现定义V=(p,q,r,u,v,w)为机体速度向量，即共轴双旋翼在机体坐标系下的速度向量，其中p、q、r、u、v、w分别为机体相对于x轴、y轴、z轴的角速度以及质心相对于x轴、y轴、z轴的速度。

基于欧拉- 庞卡莱方程建立共轴双旋翼无人机动力学模型，在机体坐标系下其方程的一般形式为

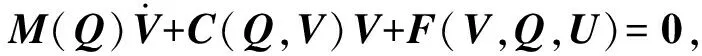
(1)

式中：Q为机体质心相对于大地坐标系下的广义坐标向量；U为控制力；M(Q)为惯性矩阵；C(Q,V)为根据欧拉动力学方程得出的变换矩阵；F(V,Q,U)为机体坐标系下包含空气动力、重力以及控制输入的总和。

(1)式中部分矩阵的具体表达式如下：

(2)

(3)

式中：m为飞行器质量；Ix、Iy和Iz分别为飞行器相对于x轴、y轴、z轴的转动惯量。

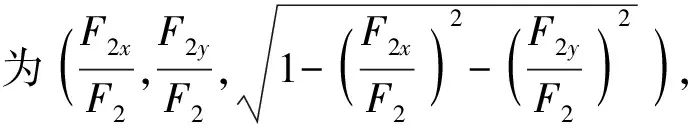
(4)

式中：F2x和F2y分别为F2在机体坐标系内x轴和y轴上的投影。将z1作为调整上旋翼系统总距离和升力大小的基准，让其随着控制器输出的F2期望值变化，则可以求解出z2和z3.

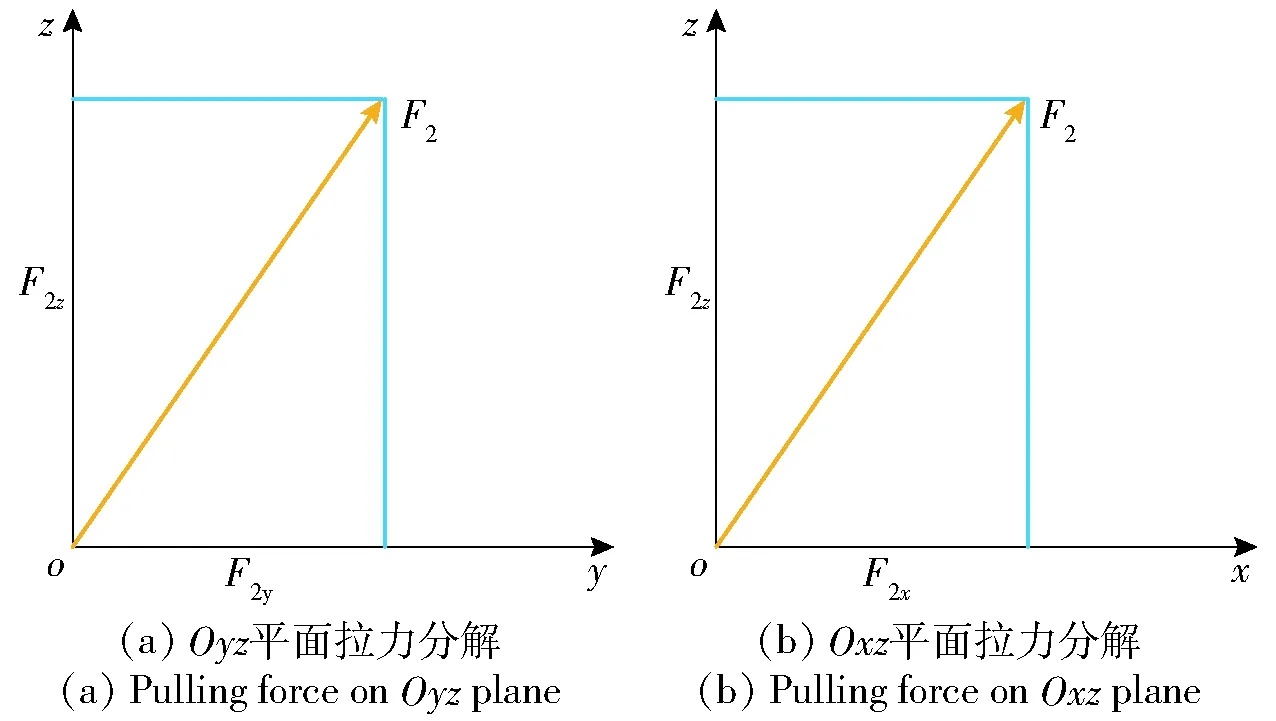
图5 上旋翼拉力分解Fig.5 Decomposition of upper rotor pulling force

飞行器质心处的受力情况由(5)式给出：

(5)

式中：

(6)

U1为垂直高度控制量，U2为滚转输入控制量，U3为俯仰控制输入量，U4为偏航控制量，η为旋转力矩系数(与旋翼受到的阻力和电机轴摩擦系数有关)；V(Q)为飞行器机体坐标系向大地坐标系转换的矩阵，为简化书写，记s()=sin (),c()=cos()，

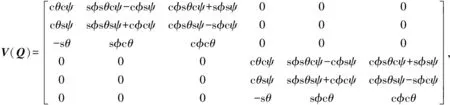
(7)

旋翼拉力可由(8)式计算得到：

(8)

式中：S为桨叶迎风面积；ρ为空气密度；Ct为旋翼拉力系数；ω为旋翼旋转角速度。根据(5)式和(6)式联立后将等式两侧同时从机体坐标系转换到大地坐标系，可以得到大地坐标系下的广义坐标向量对时间的导数：

(9)

共轴双旋翼飞行器在无风或风速很小状态下低速飞行时，空气阻力对系统的影响较小，可以忽略不计。同时，假设共轴双旋翼在飞行过程中的滚转角和俯仰角很小，且其变化率也充分小，则系统的数学模型可以简化为

(10)

由(10)式可知，飞行器质心位置的3个坐标x、y、z这3个通道之间的耦合非常严重，在考虑旋翼间气动干扰对入流动力学的影响后，其力与力矩的动态变化过程更复杂，在飞行器本体动力学的非线性之外进一步叠加了控制力产生过程的严重非线性，同时也加重了耦合问题。

2.2 上旋翼和下旋翼干扰及挥舞运动的模型

为了反映上旋翼和下旋翼之间的气动干扰，根据叶素理论和Pitt-Peters动态入流模型建立上旋翼和下旋翼入流干扰及挥舞运动模型。该方法相比涡流理论或计算流体力学(CFD)方法的形式简洁、计算方便，与实验数据也吻合较好。需要指出的是，该模型建立在以下假设基础上：桨叶为刚性，忽略桨叶根部截断效应、桨尖损失与挥舞铰外伸量，且不考虑非定常效应，认为入流速度在桨盘平面内均匀分布[12]。Pitt-Peters动态入流模型的核心思想是将诱导速度的动态变化和空气阻力变化通过(11)式联系起来：

(11)

式中：λi=[λ0,λs,λc]T，λ0、λs和λc分别表示诱导入流比的时均、1阶横向分量和1阶纵向分量；C=[Ct,Cr,Cp]T，Cr和Cp分别为旋翼滚转力矩和俯仰力矩系数；Mi、Vm和L分别为入流动力学的惯性矩阵、质量流量参数矩阵和静态传递矩阵。诱导速度的相互影响用(12)式表示为

λi=λ0,i+Kjiλ0,j+λfs，

(12)

式中：Kji表示旋翼间诱导速度干扰系数，与两组旋翼的直径和间距等设计参数有关；i、j∈{u,l},i≠j，下标l表示下旋翼，u表示上旋翼；λi为入流比；λ0,i、λ0，j为静止状态下无穷远处到某一叶片的入流比；λfs为飞行器运动带来的入流比。根据上述入流干扰模型，可以将旋翼系统的拉力和扭矩表示如下：

(13)

(14)

式中：T和Q分别为整个旋翼系统产生的拉力和扭矩；δ为叶素桨距角；Cd为桨叶阻力系数；v0,i为无穷远处到某一叶片的诱导速度；σ=Nbc/(πR)表示桨盘实度，c为桨叶弦长，Nb为桨盘上的桨叶根数；a0为翼片升力线斜率；A为桨盘面积。

另外，考虑到桨叶的刚度，挥舞运动对另外俯仰和滚转通道的正交力矩为

(15)

式中：k9=NbSβγIβΩ2/8，Sβ为叶片刚度系数，γ为桨叶洛克数，Iβ为挥舞转动惯量；αa为纵向挥舞角；αb为横向挥舞角。

综上所述，考虑挥舞运动和旋翼气动干扰后，共轴双旋翼飞行器的动力学模型修改为(其他项不变)

(16)

3 控制器设计

3.1 总体控制结构

图6所示为共轴双旋翼飞行器系统的控制结构示意图，整个控制系统可分为姿态控制和位置控制。

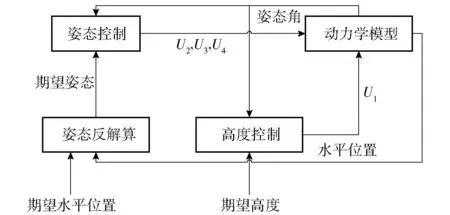
图6 控制结构图Fig.6 Control structure

由于共轴双旋翼的三轴姿态控制之间不存在耦合关系，且姿态控制响应最快，本文优先对姿态进行控制，保证其精确控制。考虑到共轴双旋翼的欠驱动问题，即4个输入控制6个自由度，直接通过PID算法建立姿态角与水平位置之间的数学关系，通过水平位置的信息解算出所需姿态角的信息，再根据姿态角和水平控制量计算高度控制量，进而通过控制姿态角和位置高度实现轨迹跟踪的目的[19]。滚转角与俯仰角的期望值分别表示如下：

(17)

式中：kp、ki、kd分别为比例、积分、微分的调节系数；φd、θd、ψd分别为期望的俯仰角、滚转角、偏航角；Xd、Yd为期望值；X、Y可以由机载传感器通过测量得到。

3.2 滑模PID控制算法

因为通常采用线性滑模面的滑模控制器会有明显的抖振，且无法通过调整参数来消除抖振，所以本文在滑动模态控制算法的基础上进行改进，将滑模面函数设计成误差项的比例、微分、积分3项相加的形式，这种算法即为滑模PID控制算法[19]。这种做法的目的在于改善滑模面的性能，相当于在滑模面附近建立一个“缓冲带”，以有效地抑制抖振。滑模控制器的一般设计步骤为：1)选取适当的PID滑模面函数s；2)设计合适的控制律，使该系统能够到达且保持在期望的滑模面s=0上。

以共轴双旋翼俯仰通道为例，定义跟踪误差为

eφ=φd-φ，

(18)

然后选取滑模面函数为

(19)

式中：λ1、λ2为控制器参数。

再根据趋近律推导控制律方程，选取指数趋近律，即

(20)

式中：ε、k为控制器参数，ε=0.2，k=1.

选取Lyapunov函数为

(21)

则有

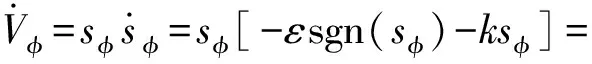
(22)

由此可知，四旋翼系统渐进稳定，跟踪误差最终收敛到0，且满足滑动模态的可达条件。

因此，由

(23)

可得

(24)

式中：c1、c2为控制器参数。

同理可得滚转角、偏航角和高度的控制律分别为

(25)

式中：d1、d2、h1、h2为控制器参数。

4 Adams/MATLAB联合仿真

4.1 仿真模型建立

首先将Solidworks2018软件中建立的装配体进行必要的简化，按照相对运动关系，将原本的202个零部件中在飞行时不存在相对运动的一组生成单个零件，则简化后整个飞行器由18个零件组成。重新将18个零件进行装配后，再依次将每个零件另存为.x_t格式，并导入Adams View中添加约束关系、力和力矩、输入及输出变量，最终输出动力学模型文件。由于Adams不具备空气动力学仿真的能力，公式中的诱导速度、桨叶阻力系数和挥舞角均取自该模型的空气动力学仿真和实验，然后将两副旋翼的拉力和扭矩作用点放置在桨盘中心，力的数值参照(11)式以函数的形式定义。

Adams中的动力学模型如图7所示。输出的文件是Simulink可读取的.slx格式，文件名为adams_sys，打开后如图8所示。动力学模型以adams_sub模块的形式与Simulink中搭建的控制模型连接，其输出就是飞行器当前的3个姿态角和质心空间坐标。

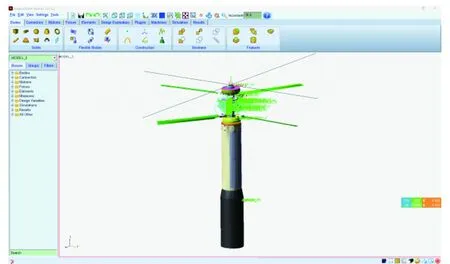
图7 Adams中的动力学模型Fig.7 Dynamics model in Adams

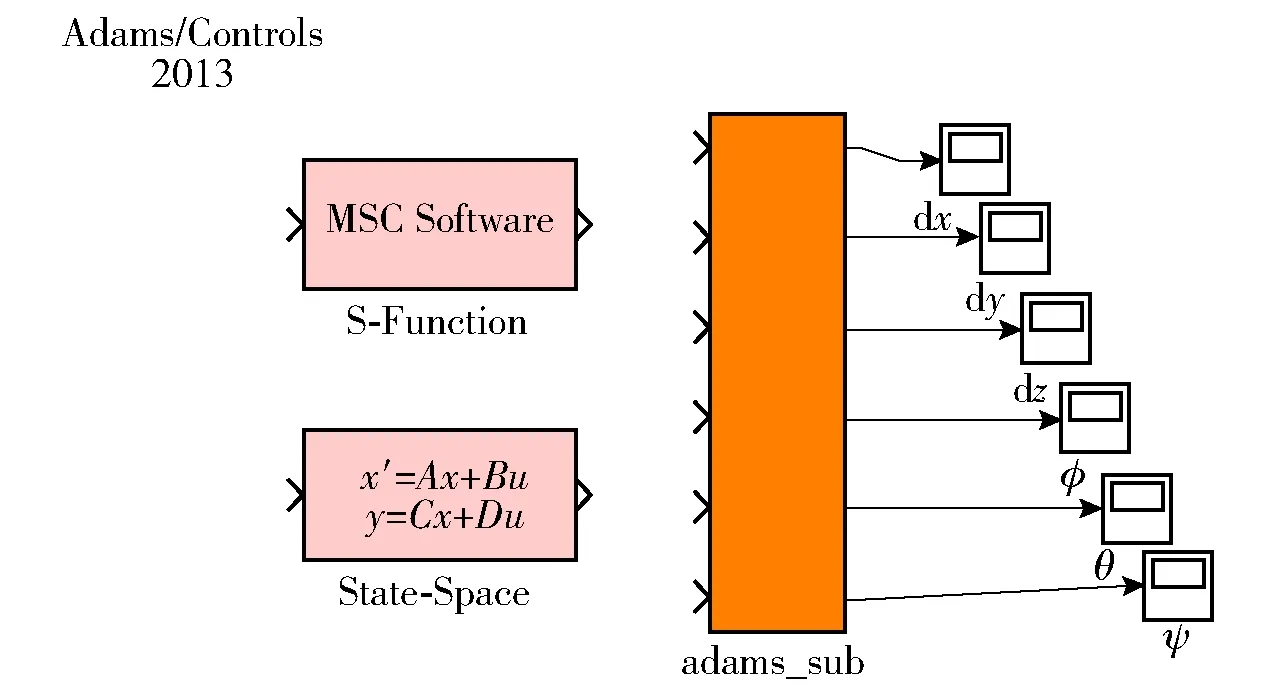
图8 Simulink中的动力学子模块Fig.8 Dynamics submodule in Simulink

在Simulink中将动力学模块的输入量和输出量通过控制算法建立起关系，在MATLAB/Simulink软件中将模块组装成控制器，并添加适当的自定义函数。由于控制律中存在关于飞行器质量和转动惯量等信息，需要在程序运行之前对这些信息进行初始化，本文采用运行m文件的方法，将所有初始化的常量写入同一文件中，运行后上传到Workspace中，运行Simulink的模型后便可以被调用，从而方便了统一修改和管理，比其他方法更加简便[20]。

整个仿真模型搭建完成后如图9所示，橙色模块即为Adams中的动力学模型。

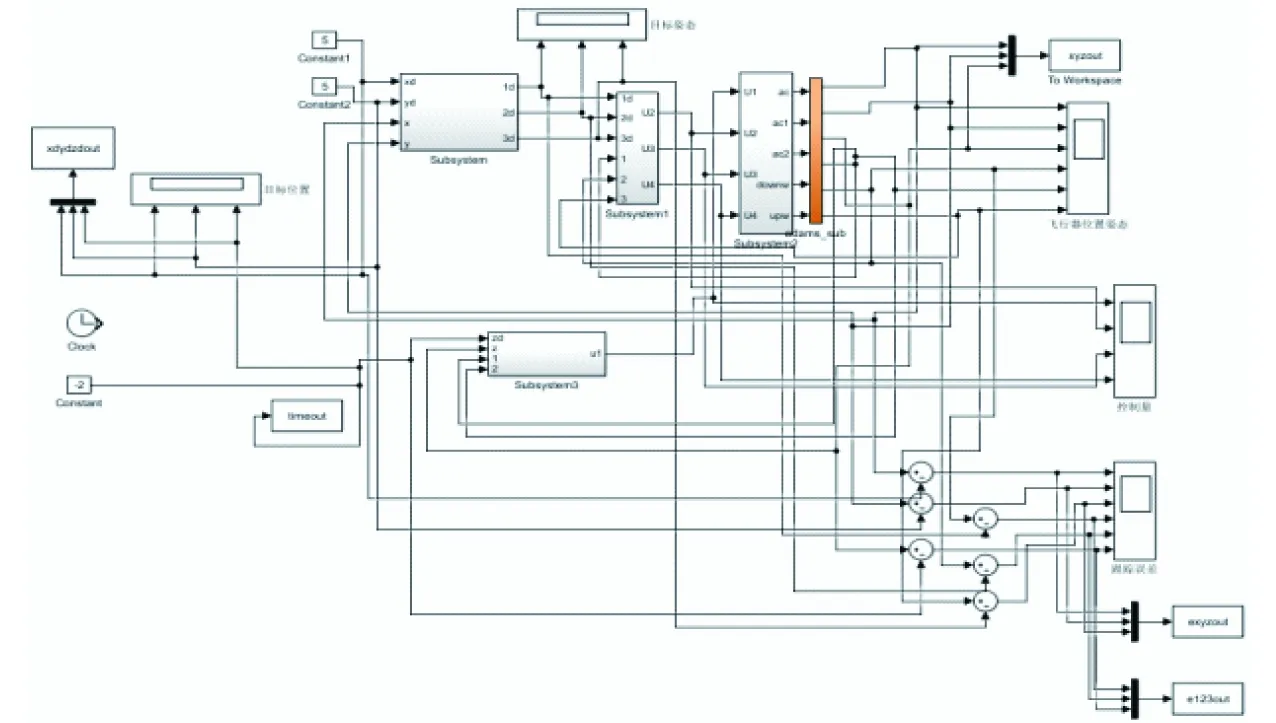
图9 Simulink中的仿真模型Fig.9 Simulation model in Simulink

由于直接对飞行器上的3个舵机进行控制，这里对飞行器动力学模型输入的量为3个舵机偏转角度τ1、τ2、τ3以及上、下2个电动马达的转速ω1和ω2. 3个舵机选用相同型号规格的步进电机，2个电动马达也完全相同，暂不考虑它们内部的响应问题。上文中已经建立了4个控制量U1、U2、U3、U4的关系式，下面对其进行转化，设计一定的规则，将U1、U2、U3、U4转化为τ1、τ2、τ3、ω1和ω2共5个输入量。

(26)

式中：Δz1、Δz2、Δz3分别为3个舵机对上旋翼升力面相应支撑点造成的z轴方向位移范围;Δτ为相应的步进电机转动范围，联立(4)式即可求出5个输入量。

4.2 悬停仿真结果

系统仿真的初始值为

X0=[0 m，0 m，0 m，0 rad，0 rad，0.1 rad，0 m/s，
0 m/s，0 m/s，0 rad/s，0 rad/s，0 rad/s]，

式中：从左至右依次为系统位置x、y、z以及姿态角φ、θ、ψ、速度和角速度。

控制器中的参数按照固定步长在一定范围内循环搜索测试，逐步缩小范围和步长，最终确定了某种意义上的最优参数组合，如表1所示。

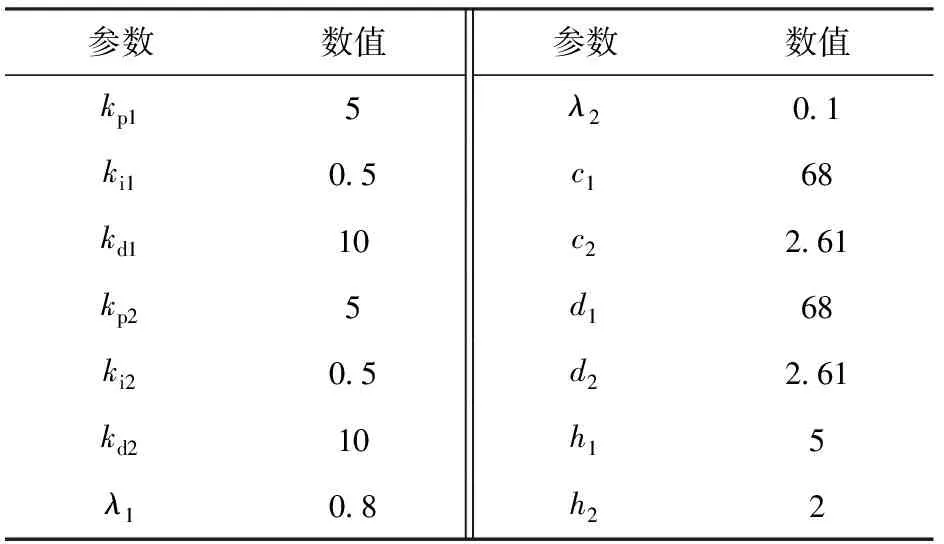
表1 控制器参数表

飞行器结构尺寸参数和气动参数如表2所示。

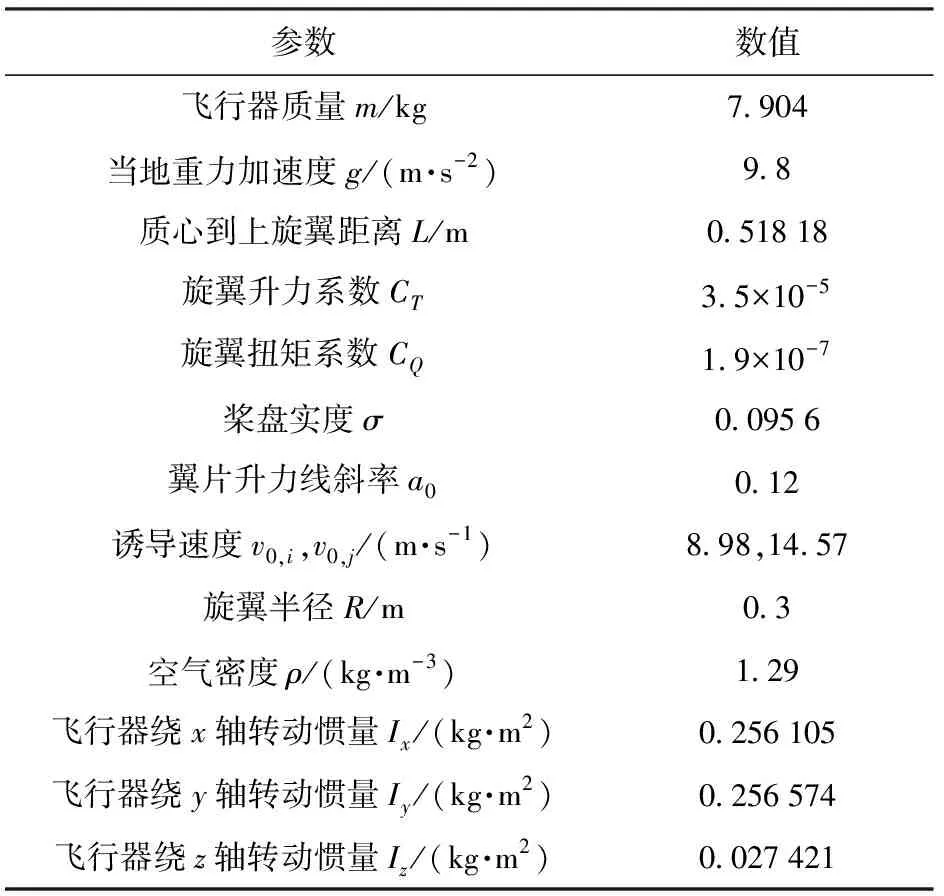
表2 飞行器动力学参数

诱导速度场实际上并不是空间均匀分布的，并且与旋翼转速有关，这里只取1个平均值。当设置目标位置坐标与初始位置相同时，仿真得到的三维运动轨迹以及位置和姿态随时间变化曲线如图10和图11所示。

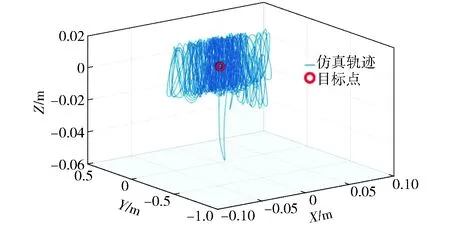
图10 原地悬停轨迹Fig.10 In-place hover trajectory

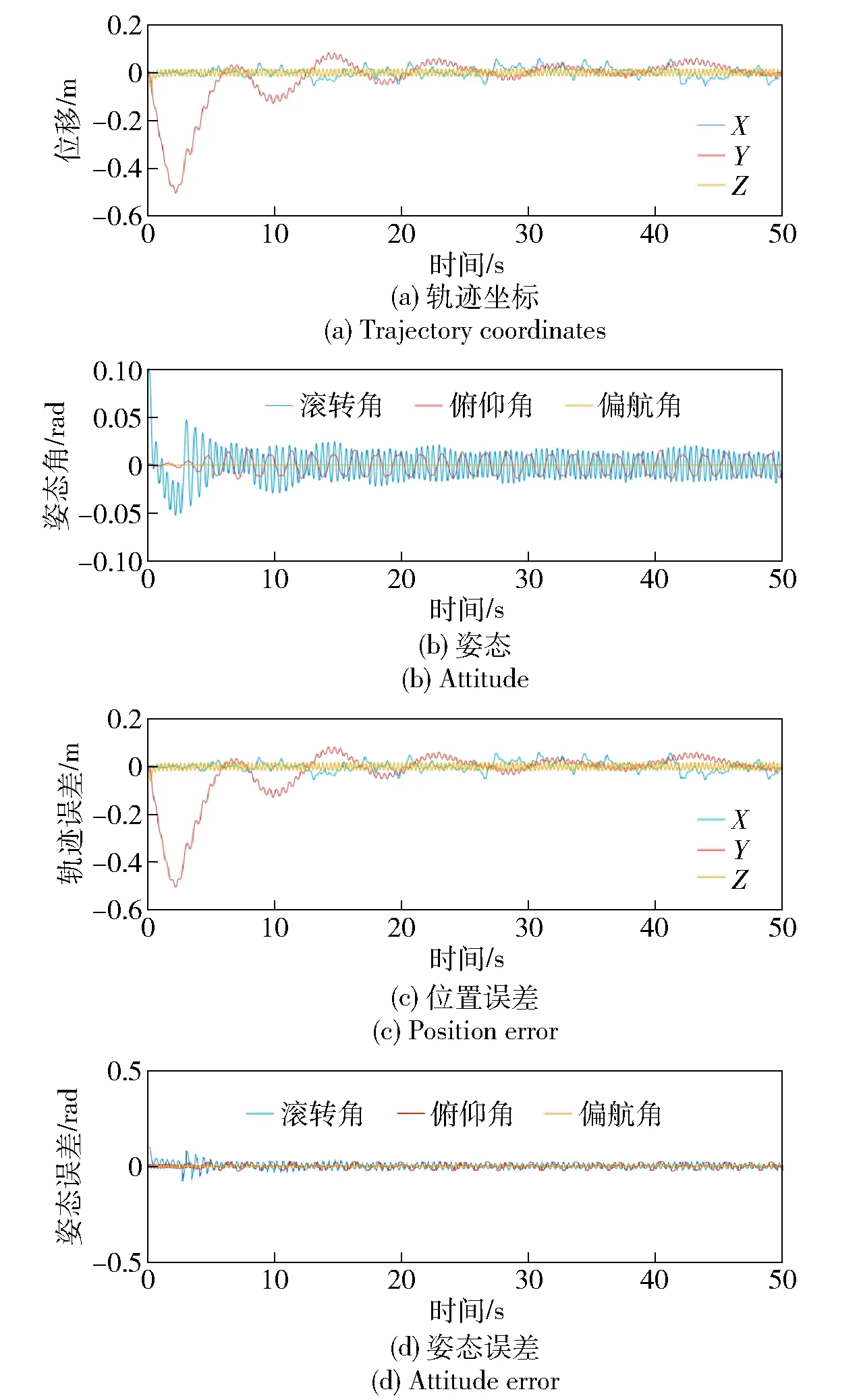
图11 悬停仿真结果Fig.11 Hover simulated results

三维轨迹图中红色圆圈代表悬停的目标位置(0 m，0 m，0 m)，从位移随时间变化曲线中可以看出：飞行器的悬停位置基本稳定，并随时间变化逐渐趋于稳定，后半段的较稳定状态时飞行器的位置三轴坐标均在(-0.05 m，0.05 m)范围内；姿态角一直存在小幅度震荡，这是因为用PID算法计算姿态角动态误差较大以及对系统建模仍然存在一定误差。从位置误差曲线可以看出，在后半段较稳定状态时飞行器的悬停位置误差在(-0.05 m，0.05 m)范围内，姿态角与姿态角期望值之间的误差几乎为0°，表明系统姿态跟踪性能较好。

程序运行完成后，会生成.res文件记录仿真结果。在Adams中导入后可以观察此次运行的动画，通过动画直观感受飞行器的运动状态，找出需要改进的位置。图12采用图像叠加的方法将动画中从某一固定观察角度且相同间隔时刻的画面以不同透明度显示到同一张图片中，更加直观地展示了飞行器运动过程。

图12 悬停动画截图Fig.12 Hover animation screenshots

当设置目标位置坐标与初始位置不同时，设定目标位置坐标(2 m，2 m，2 m)，仿真得到的三维运动轨迹以及位置、姿态随时间变化曲线和动画截图如图13、图14和图15所示。

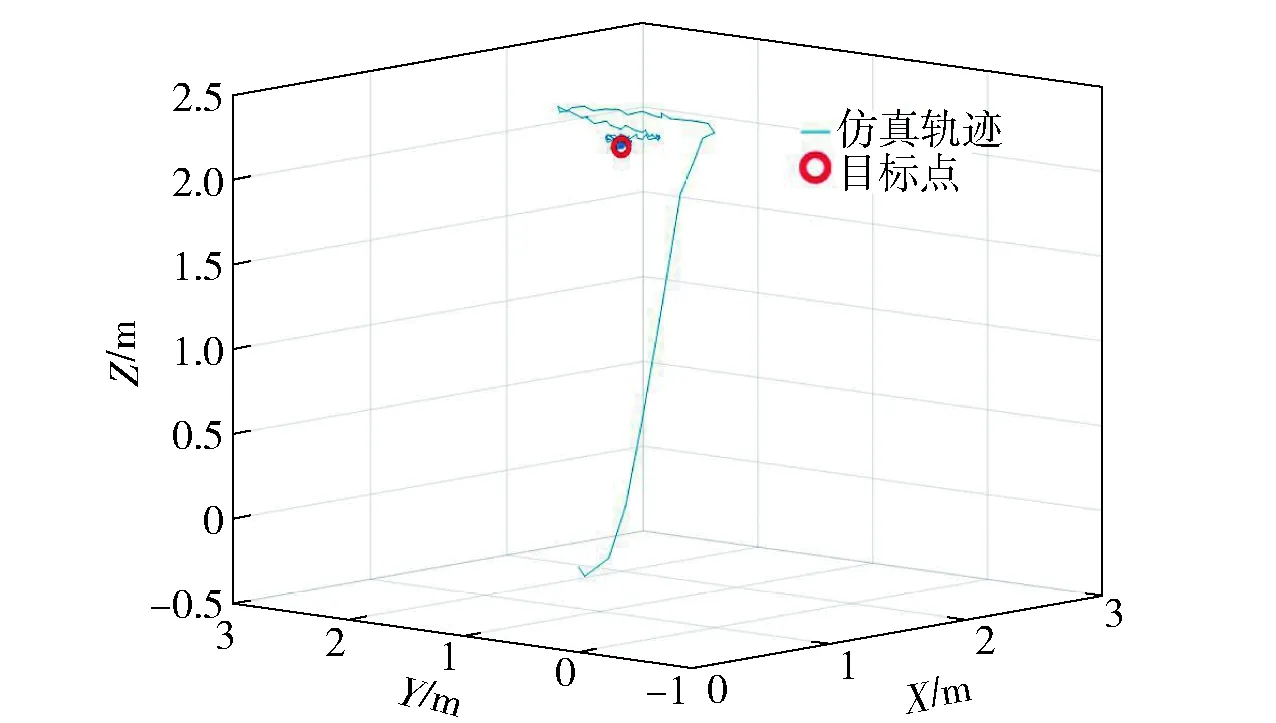
图13 移动悬停轨迹Fig.13 Move-hover trajectory

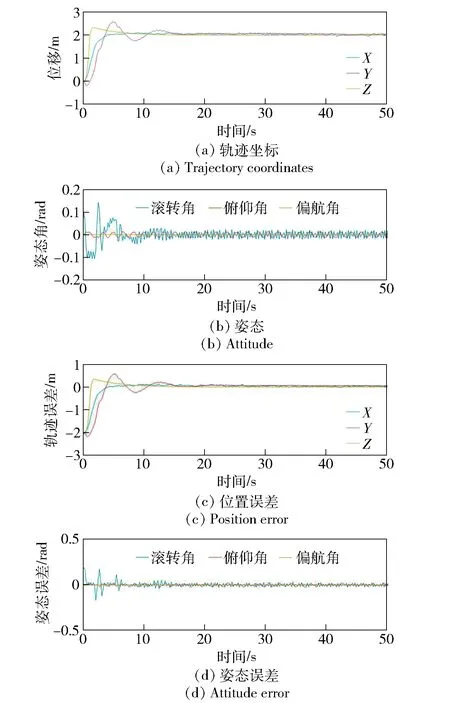
图14 移动悬停仿真结果Fig.14 Move-hover simulated results

图15 移动悬停动画截图Fig.15 Move-hover animation screenshots

由图13～图15可以看到，在经过初始短暂的超调和震荡后，依旧可以稳定在目标位置附近，说明本文所设计的控制器性能可以满足要求。

4.3 抗干扰仿真结果

在Adams View中，在飞行器质心处添加3个正交力和3个正交力矩，数值大小利用随机函数生成，用来模拟施加干扰力和力矩，测试控制器的抗干扰性能。干扰力和力矩的最大值分别为2 N和1 N·m，干扰施加的频率设置为10 Hz，干扰作用的时间范围是仿真开始后的20～25 s. 加入干扰后的仿真结果如图16所示。

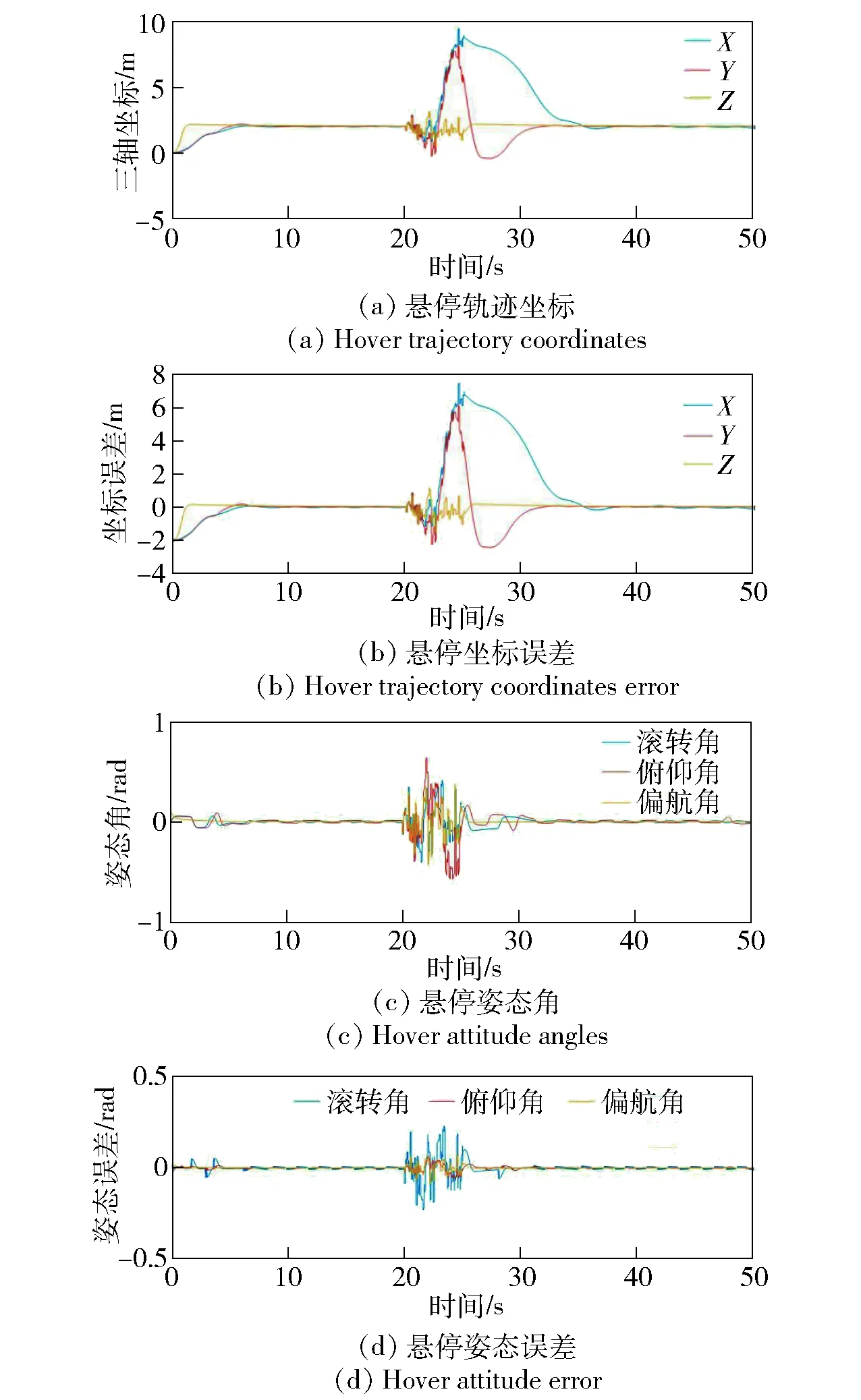
图16 加入干扰后悬停仿真结果Fig.16 Hover simulated results under interference

由图16可以看到，在持续作用的随机干扰结束后，飞行器姿态可以在5 s后恢复到稳定状态，质心位置可以在8 s后恢复到悬停的目标位置。在干扰作用5 s内，姿态角仍然可以稳定在较小的范围内，质心位置有发散趋势，这是因为干扰力变化频率太快，超过了飞行器机动调整能力，使得飞行器姿态误差一直保持在较大的范围内，这种误差经过积分放大后就导致了质心位置的偏移。如果干扰作用时间较短，类似于脉冲形式，则飞行器位置质心受到的影响就大大减小。加入脉冲干扰后悬停轨迹坐标如图17所示。

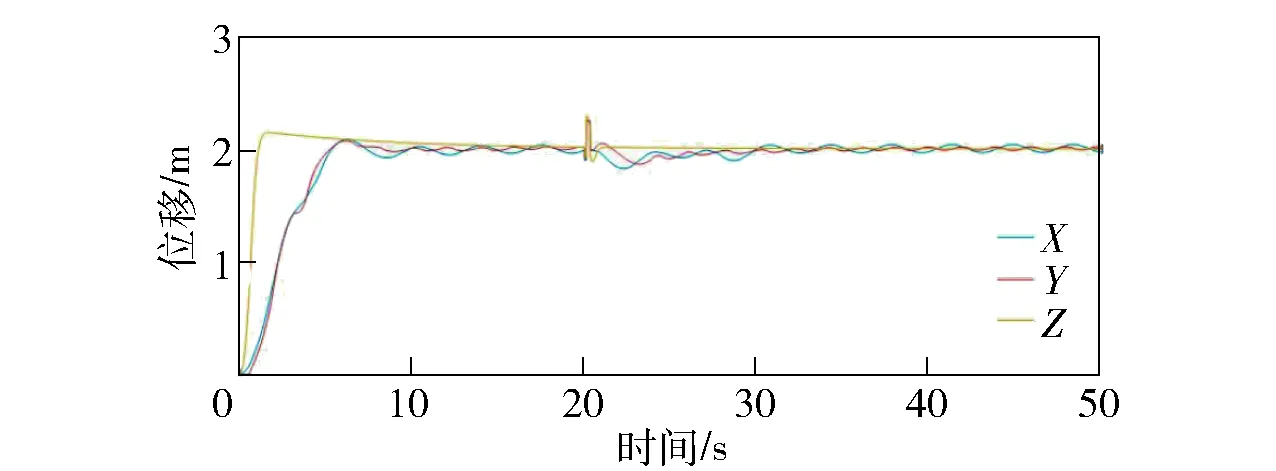
图17 加入脉冲干扰后悬停轨迹坐标Fig.17 Hover simulated results under pulse interference

5 结论

本文首先介绍了实验室在研的一种共轴双旋翼飞行器结构和工作原理；然后结合Pitt-Peters动态入流模型，建立了共轴双旋翼飞行器的动力学模型，并基于滑模PID算法设计了对应的控制器；最后利用Adams/MATLAB联合仿真技术进行了飞行器飞行控制仿真，分别对悬停，移动悬停，悬停中持续干扰和脉冲干扰4种情况的仿真结果进行了分析。所得主要结论如下：

1)本文所设计的控制器直接对飞行器舵机和电动马达进行控制，使MATLAB中控制模型与实际的飞行器飞控芯片内代码非常接近，从而使得仿真结果更具有可信性。

2)从仿真结果中可以看出，飞行器具备了较好的悬停稳定性、抗干扰性能和一定的机动能力。飞行器在控制器作用下的位置和姿态均得到了有效控制，悬停性能完全满足要求。

3)在仿真结果的稳定阶段(t>20 s)，姿态角仍然存在震荡，意味着舵机和电机工作状态也在高频率的震荡，会对舵机和电机的寿命造成一定的损害。主要原因为通过PID算法直接建立期望姿态和水平位置的映射关系时并没有考虑到飞行器动力学属性，下面的工作中重点考虑改进这一部分算法，使飞行器姿态得到更好的收敛。