硬脆材料切割过程中基于线锯速度的切割力自适应控制

安蓓， 李淑娟， 郝政， 赵雯， 王嘉宾， 梁列

(西安理工大学 机械与精密仪器工程学院, 陕西 西安 710048)

0 引言

目前，应用于硬脆材料切割的主要技术是游离磨料和固结金刚石磨料线锯切割技术两种，其中固结金刚石磨料线锯切割技术具有切缝窄、切片质量好、切割效率高等优点[1]，成为硬脆材料切割的主流技术。国内外在该方面进行了很多研究，Ishikawa等[2]观察发现当工件材料直径达到6 inch以上时，采用游离磨料线锯切割技术会增加切割时间，并且切割圆形工件时难以向其中心供应磨料。Hardin等[3]研究用固结金刚石磨粒线锯技术切割单晶SiC时的表面粗糙度，结果表明了该方法切割脆性材料的可行性。Clark等[4]探讨采用固结金刚石磨粒线锯技术切割硬脆材料时各工艺参数对切割力和表面粗糙度的影响，结果表明了该工艺研究的必要性。Liedke等[5]通过实验建立线锯切割加工过程中的宏观力学模型，研究了加工过程中切割力的变化与各工艺参数如进给速度、线锯速度之间的关系。Li等[6]分析SiC单晶切割过程中的工艺因素，通过实验建立了进给速度与切割力的动态切割力模型。Cvetkovi等[7]提出单晶和多晶SiC的划线切割和线锯切割两种加工方法，并对比了这两种方法的优点和缺点。王嘉宾等[8]对切割力的动态变化因素从机理上进行分析，建立了线锯加工圆形工件过程模型，研究了不同加工参数下接触弧长的变化趋势。高玉飞等[9]通过往复式金刚石线锯切割单晶硅片的实验，对线锯速度和进给速度等加工参数对硅片表面质量的影响进行了分析。

综上所述，已有的硬脆材料切割研究大多属于针对切割过程中工艺参数对切割力或表面粗糙度的影响进行分析，部分为线锯切割机理研究。本文在研究进给速度与切割力的控制模型的基础上[6]，以提升切片表面质量为目标，提出了往复式固结金刚石磨粒线锯切割硬脆材料过程中切割力的控制方法。首先分析线锯速度对切割力的影响规律，建立直接数字控制(DDC)系统，并采用最小方差自校正控制(MVC)策略设计切割力控制器，实时测量切割力与线锯速度的对应变化关系，对其进行实时分析和控制；然后采用LabVIEW编程语言开发金刚石线锯切割软件系统；最后通过实验验证了所提出的自适应控制策略的可行性和高效性。本文成果可对硬脆材料切割加工的控制研究提供一定的指导。

1 切割原理和设备

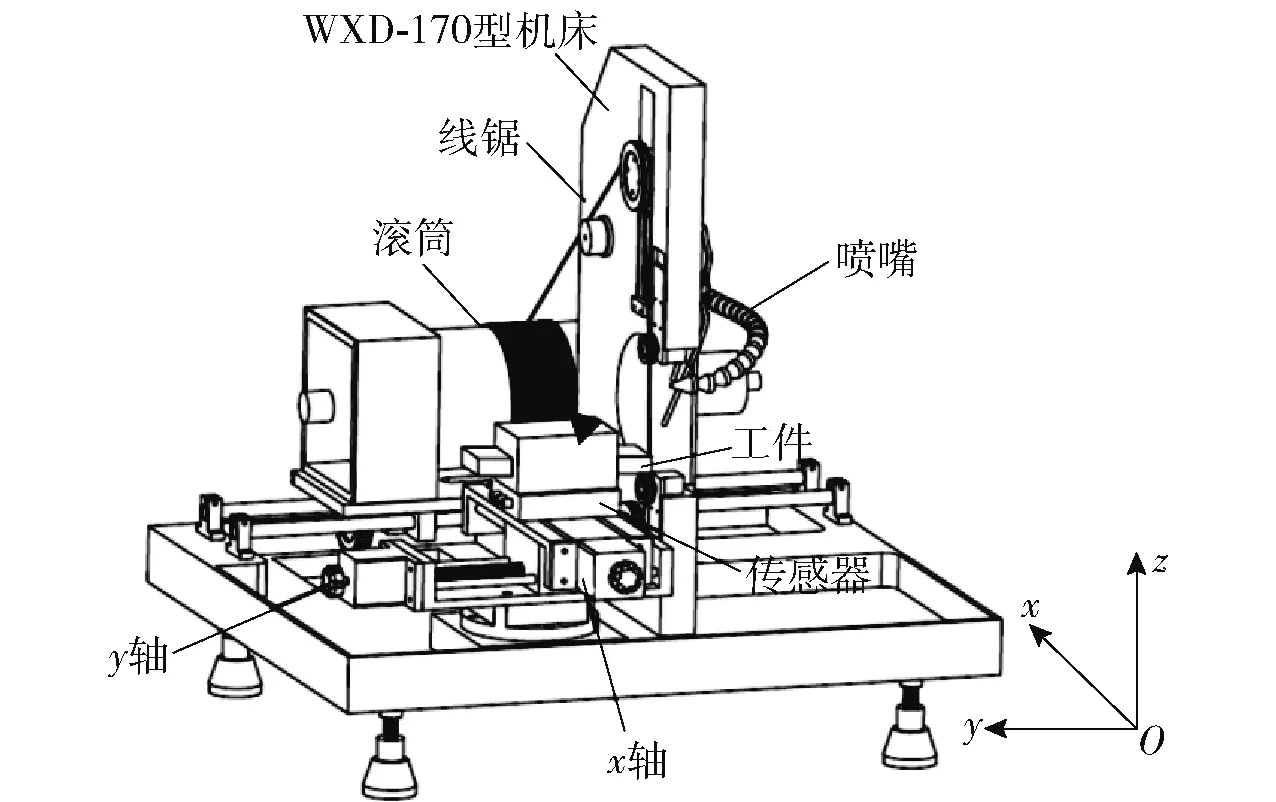
图1 往复式线锯旋转点切割机床简图Fig.1 Schematic diagram of reciprocating wire cutting machine

实验设备选用改装的沈阳麦科材料加工设备有限公司生产的WXD-170型往复式固结金刚石磨粒线锯旋转点切割机床，如图1所示。由图1可见，线锯切割过程由工作台移动和线锯往复运动共同实现。由深圳雷赛公司生产的57两相型步进电机驱动工作台x轴、y轴方向的运动。电机驱动x轴移动平台实现工件的进给运动，进给速度调节范围为0.005～18 mm/min；电机驱动y轴移动平台设定切片厚度，y轴移动行程为0～120 mm. 线锯的往复运动可由正反向旋转的卷线滚筒带动，线锯由一对张紧轮和一对工作导轮进行支撑，线锯速度在0～3 m/s之间无级可调。金刚石线锯胎体为镍，镀有JR2型金刚石磨粒。切割力测量装置采用美国ATI公司生产的GAMMA-R-8-2-M1 USB测力仪，可分别测出x轴、y轴、z轴 3个方向的力，Fx、Fy、Fz的测量范围分别为-65～65 N，-65～65 N，-200～200 N，采样频率设定为1 kHz. 被切割工件选用光学玻璃，其尺寸为220 mm×20 mm×26 mm.

2 建立静态切割力模型

为了充分研究往复式固结金刚石磨粒线锯切割工件时线锯速度与法向切割力的关系模型。实验中分别以线锯速度vs、工件进给速度vx为可变因素，设计如下6组实验。表1为实验中所使用的工艺参数以及切割力的对应情况。表1中Fn为法向切割力，t为切割时间。

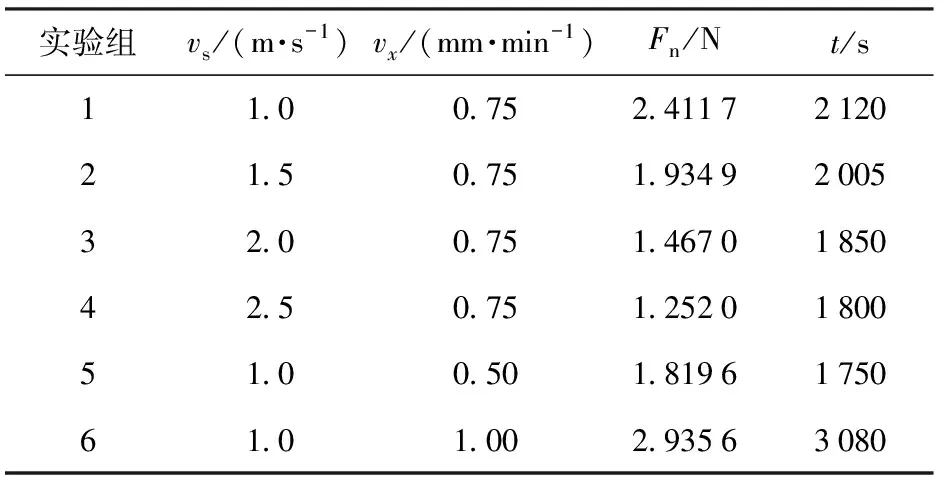
表1 线锯速度和进给速度恒定情况下法向 切割力的对应情况

图2所示为线锯速度分别为1.0 m/s、1.5 m/s、2.0 m/s、2.5 m/s时法向切割力的变化波形图。

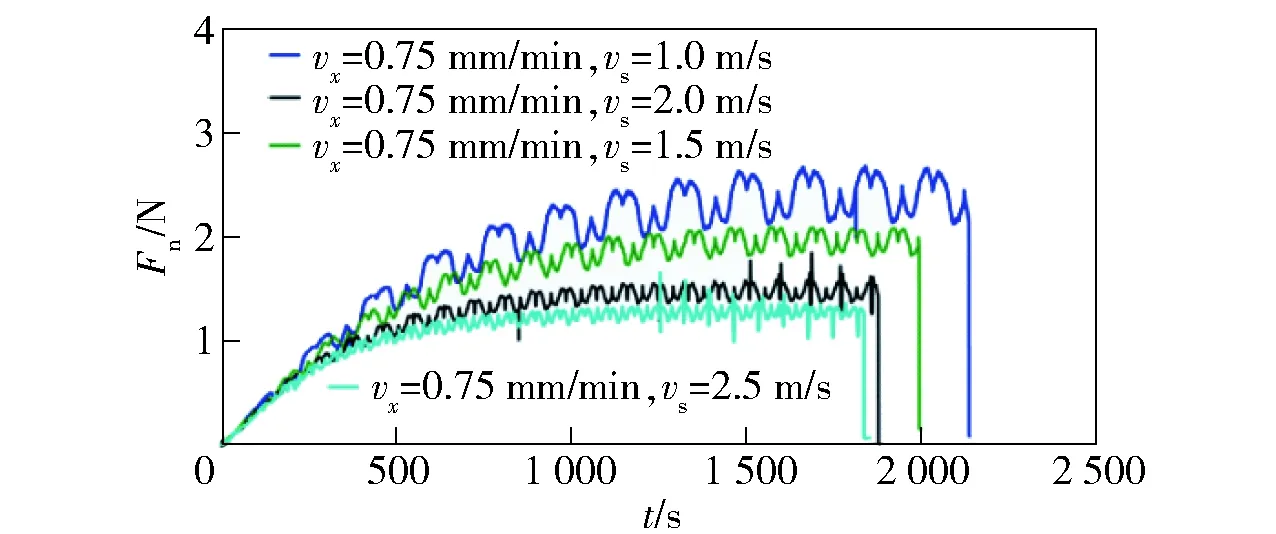
图2 不同线锯速度下法向切割力的变化波形图Fig.2 Normal cutting forces at wire saw velocities of 1.0 m/s, 1.5 m/s, 2.0 m/s, and 2.5 m/s

从图2中可以看出：随着线锯速度的增加，法向切割力越小；线锯速度越大,完成一个往复切割运动的时间越短。图3所示线锯速度为线锯速度为1.5 m/s时法向切割力与线锯速度的对应关系，图4所示为其对应关系的放大图。

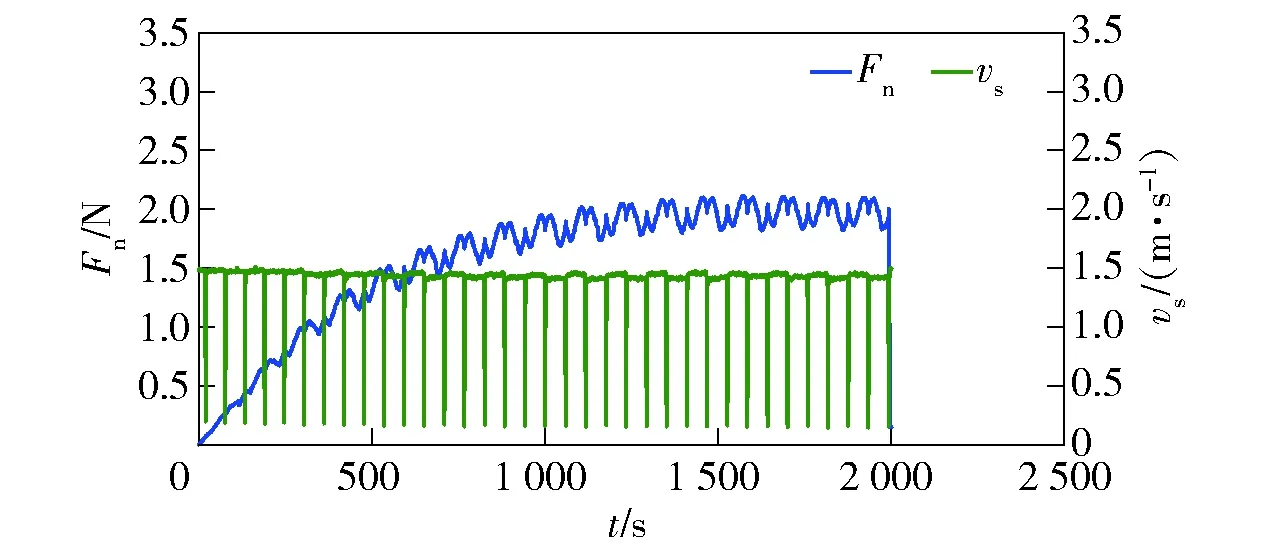
图3 平稳切割阶段线锯速度与法向切割力对应关系图Fig.3 Normal cutting force and wire saw velocity during steady processing

图4 平稳切割阶段线锯速度与法向切割力对应关系 局部放大图Fig.4 Partial enlarged detail of normal cutting force and wire saw velocity during steady processing

建立如下静态切割力模型[10]：

(1)

式中：Kn为系数；α、β分别为工件进给速度和线锯速度的指数系数。

将表1所得的切割力模型实验测量数据代入(1)式，采用最小二乘法拟合得到金刚石线锯切割静态模型参数值为

Kn=2.964 1，α=0.694 1，β=-0.705 9.

(2)

为了保证一定的切割效率，在进行线锯速度与法向切割力的实验研究中，固定进给速度为vx=0.75 mm/min，故可得到线锯速度与切割力的对应变化关系为

(3)

式中：Ks为系数，根据实验拟合结果可得Ks=2.43.

3 切割力的自适应控制过程建模

3.1 切割力自适应控制器的结构

本文所提出的往复式固结金刚石磨粒线锯切割硬脆材料的自适应控制结构框图如图5所示。由图5可知，在对切割过程进行跟踪控制的过程中，Fr表示期望的切割力值，vs(k)为k时刻通过金刚石线锯切割自适应控制系统计算得到的输入线锯速度值，v(k)表示金刚石线锯切割加工系统的振动和噪声等干扰因素，Fn(k)为被控对象在k时刻输出的切割力。将vs(k)和Fn(k)不断输入最小二乘递推参数估计器进行采样辨识，辨识出线锯切割系统的参数。最后，由切割力控制器和参数估计器组成系统自适应控制策略。

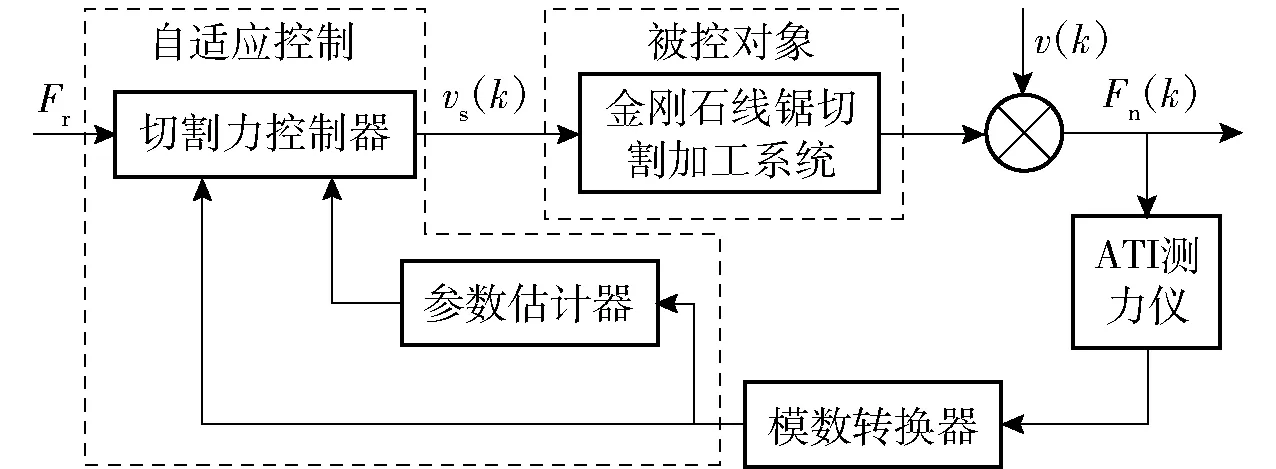
图5 金刚石线锯切割硬脆材料的自适应控制结构框图Fig.5 Block diagram of adaptive control structure for diamond wire saw cutting hard and brittle materials

3.2 最小方差自校正控制律设计

本文采用最小方差间接自校正控制，由于被控对象参数未知，首先利用递推最小二乘法实时在线计算系统参数，然后设计最小方差控制律。根据自动控制理论可知，模型过程的研究包括模型阶次的辨识和模型参数的辨识。

选用行列式比法来判定金刚石线锯切割系统中线锯速度与切割力的模型阶次[11]，选用逆M序列为激励系统的输入信号，根据该往复式切割设备，给定逆M序列中线锯速度的范围为0.5～3.0 m/s，如图6所示。采集到的输出切割力信号如图7所示。

建立金刚石线锯切割系统的过程模型为

(4)

式中：vs(k)为该系统辨识输入信号，即线锯速度；

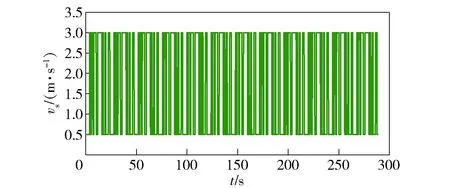
图6 系统辨识输入信号(线锯速度)Fig.6 Input signal identified by system (wire saw velocity)

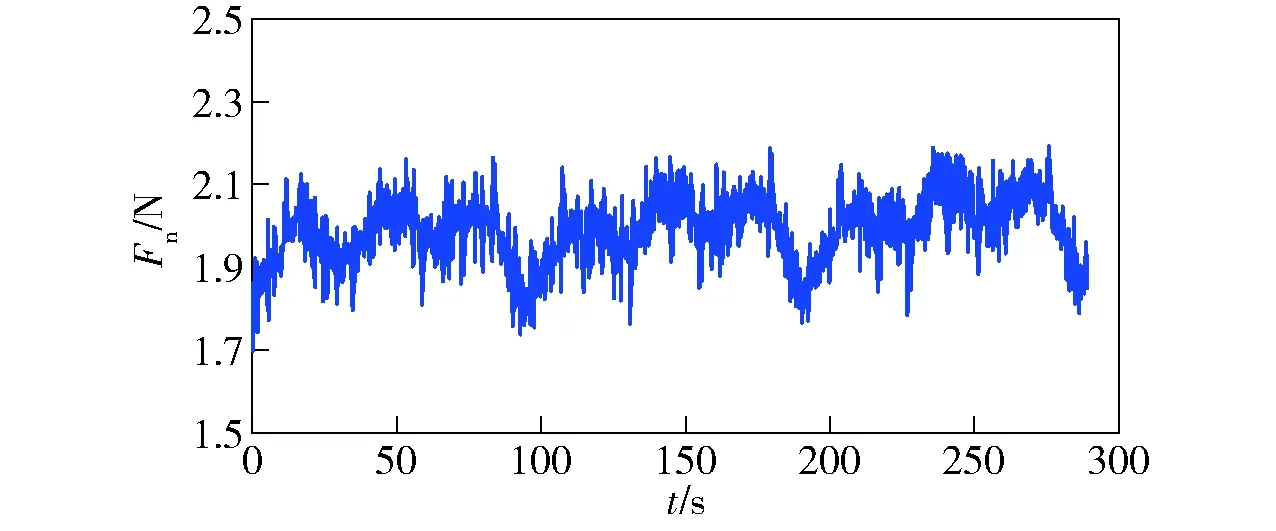
图7 系统辨识输出信号(法向切割力)Fig.7 Output signal identified by system (normal cutting force)

Fn(k)为该系统辨识输出信号，即法向切割力；v(k)为机床运行过程中的噪声以及振动扰动，将其视为白噪声；ai、bi为多项式系数；i为求和运算中的变量；n为模型阶次。

根据上述采集的数据信号，估计模型阶次为n，可得到如下数据矩阵：

(5)

式中：L为所采集的数据长度。

构造金刚石线锯切割系统的行列式比为

(6)

式中：

(7)

当系统阶次n从1开始逐次递增时，若DR(n)比DR(n-1)有显著增加，则可确定系统模型的真实阶次为n0=n. 由行列式比法辨识得到系统模型的阶次如图8所示。

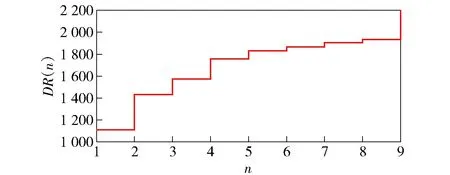
图8 行列式比法辨识的系统模型阶次Fig.8 System model order identified by determinant ratio method

因此，可确定在往复式固结金刚石磨粒线锯切割系统中，线锯速度与法向切割力构成的系统模型阶次为2阶。

工业中采用的自动控制反馈技术均为负反馈，但在固结金刚石线锯切割加工系统中，线锯速度增大，法向切割力反而减小，故该往复式金刚石线锯系统为正反馈系统。因此在构建系统的控制模型中需要采取中间变量，即

(8)

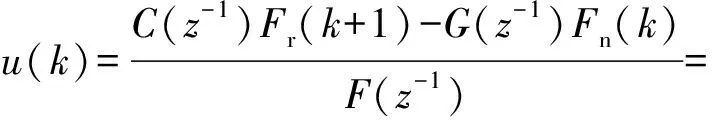
(9)

式中：C(z-1)、G(z-1)、F(z-1)表示丢番方程中的多项式；1、2、0、1为实时估计的模型参数；Fr(k+1)为k+1时刻的参考力，本文中为定值。

故由u(k)=vs(k)-0.705 9可得，输出的线锯速度为

vs(k)=[u(k)]-1.42.

(10)

4 结果分析

4.1 切割力的实验验证

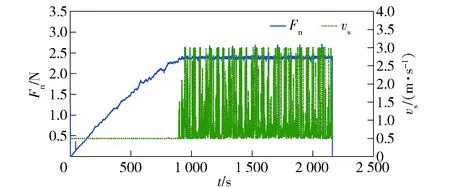
图9 参考力为2.40 N的法向切割力和线锯速度关系图Fig.9 Relation between normal force and wire saw velocity with reference force of 2.40 N

将MVC控制器应用于固结金刚石磨粒线锯切割系统中，跟踪大小不同的参考力，结果如图9～图14所示。参考力Fr分别为2.40 N、1.90 N和1.48 N，对应于进给速度为0.75 mm/min以及线锯速度分别为1.0 m/s、1.5 m/s和2.0 m/s的恒定参数切割。在线锯切割加工初期，线锯速度以最小速度运行，直至达到给定参考力附近时，线锯速度会进行连续变化调节。与定参数切割相比，切割力上下波动很小，只是在换向时线锯速度会发生突变、出现尖点。

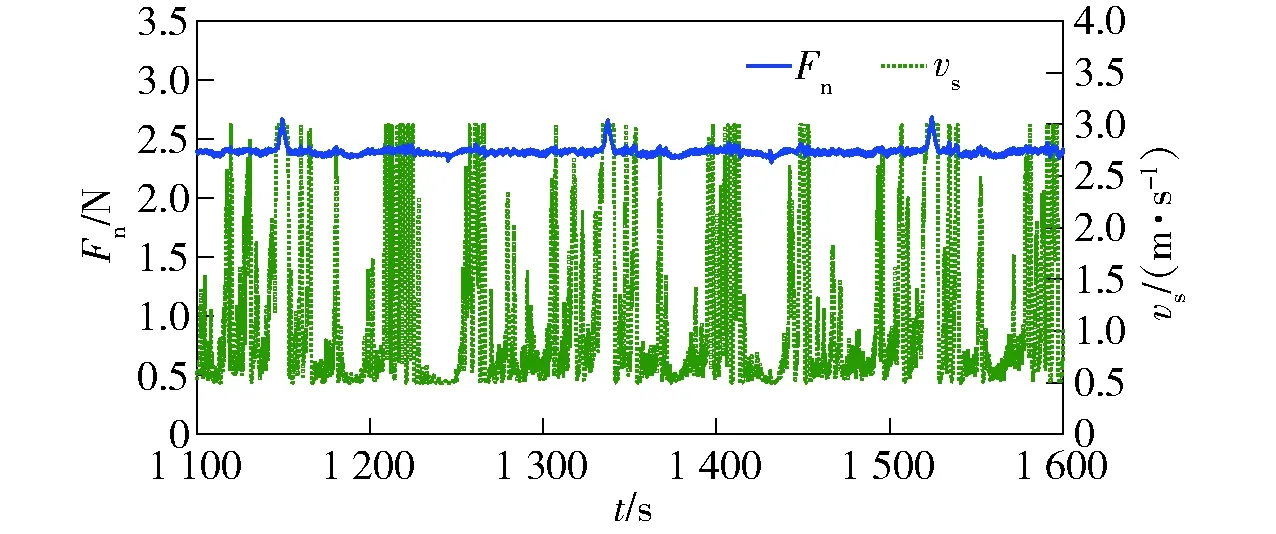
图10 参考力为2.40 N的法向切割力和线锯速度 局部放大图Fig.10 Partial enlarged detail of normal force and wire saw velocity with reference force of 2.40 N

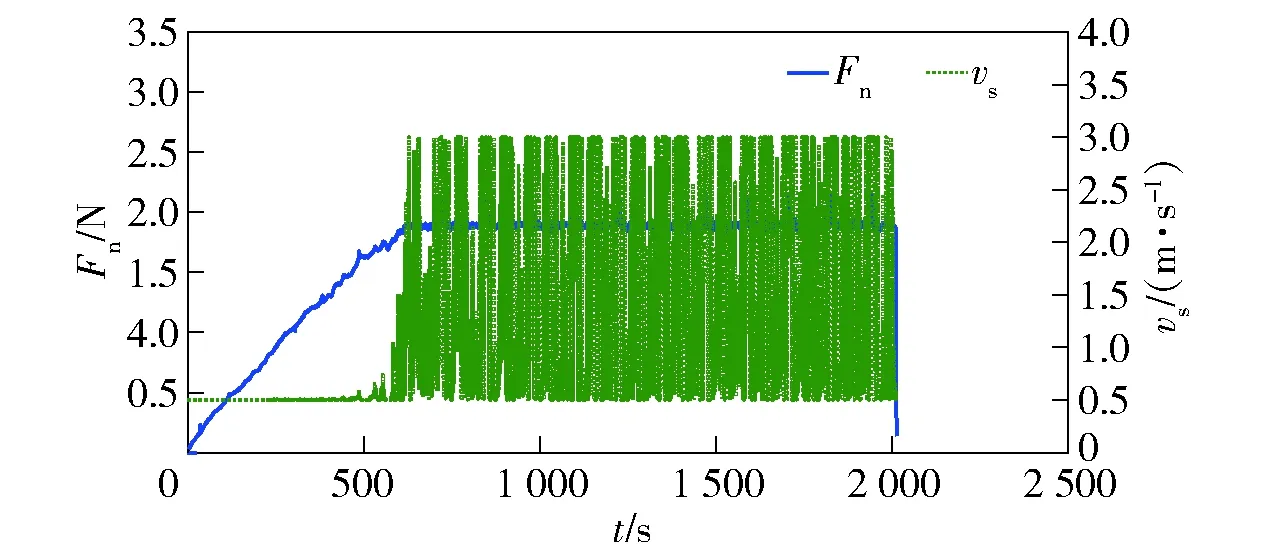
图11 参考力为1.90 N的法向切割力和线锯 速度关系图Fig.11 Relation between normal force and wire saw velocity with reference force of 1.90 N

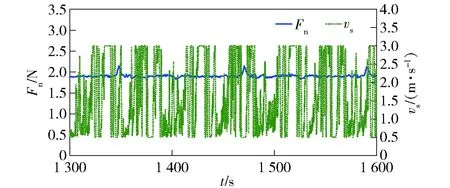
图12 参考力为1.90 N的法向切割力和线锯速度 局部放大图Fig.12 Partial enlarged detail of normal force and wire saw velocity with reference force of 1.90 N

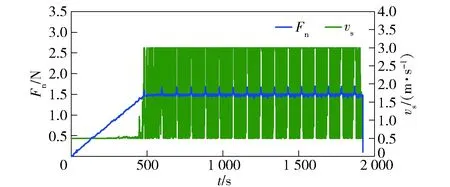
图13 参考力为1.48 N的法向切割力和线锯速度关系图Fig.13 Relation between normal force and wire saw velocity with reference force of 1.48 N

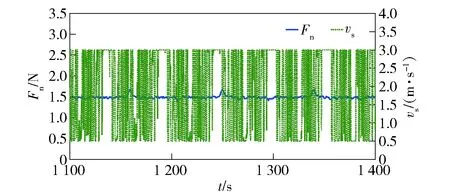
图14 参考力为1.48 N的法向切割力和线锯速度 局部放大图Fig.14 Partial enlarged detail of normal force and wire saw velocity with reference force of 1.48 N

定参数切割和采用最小方差自校正控制策略切割的结果对比如图15和图16所示。

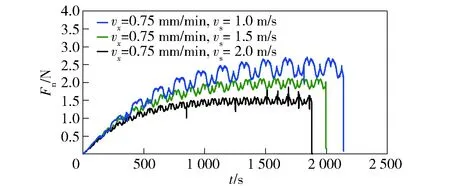
图15 普通定参数加工的切割力Fig.15 Cutting force under the condition of constant parameters

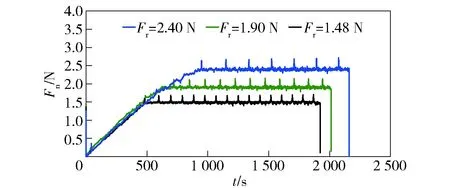
图16 采用MVC控制器加工的切割力Fig.16 Cutting force processed with MVC

4.2 表面粗糙度对比

采用德国徕卡公司的 DCM-3D光学显微镜对恒定参数和采用最小方差自校正控制加工的工件表面形貌[12]进行测量，沿进给方向，在切割力平稳状态每片切片取4个点。测量范围为1.329 9 mm×0.496 1 mm. 选用区域形貌粗糙度评定参数Sa作为切片表面粗糙度的评定标准，Sa的计算公式为

(11)

式中：N和M分别为测量区域中x轴和y轴方向的采样点数；z为测量区域内表面轮廓到基准平面的高度。测量区域的长度方向与工件进给方向相同，测量区域的宽度方向垂直于进给方向。则不同线锯速度下切片的表面形貌图如图17～图22所示。其中：图17、图19、图21为恒定线锯参数下线锯速度分别为1.0 m/s、1.5 m/s和2.0 m/s的表面粗糙度，其值分别为5.89 μm、3.87 μm和2.48 μm；图18、图20、图22为采用最小方差自校正控制的表面粗糙度分别为4.21 μm、2.51 μm和1.55 μm.

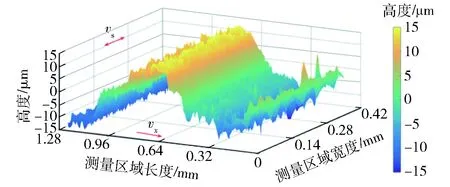
图17 线锯速度1.0 m/s的切片表面形貌图(Sa=5.89 μm)Fig.17 Surface morphology with the wire saw velocity of 1.0 m/s (Sa=5.89 μm)

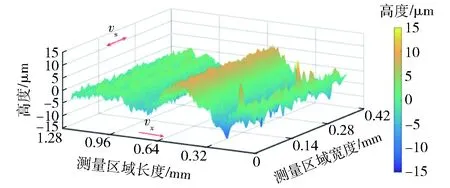
图18 参考力为2.40 N和最小方差自校正控制 的表面粗糙度图(Sa=4.21 μm)Fig.18 Surface roughness for minimum variance self-tuning adaptive control experiment for Fr =2.40 N (Sa=4.21 μm)

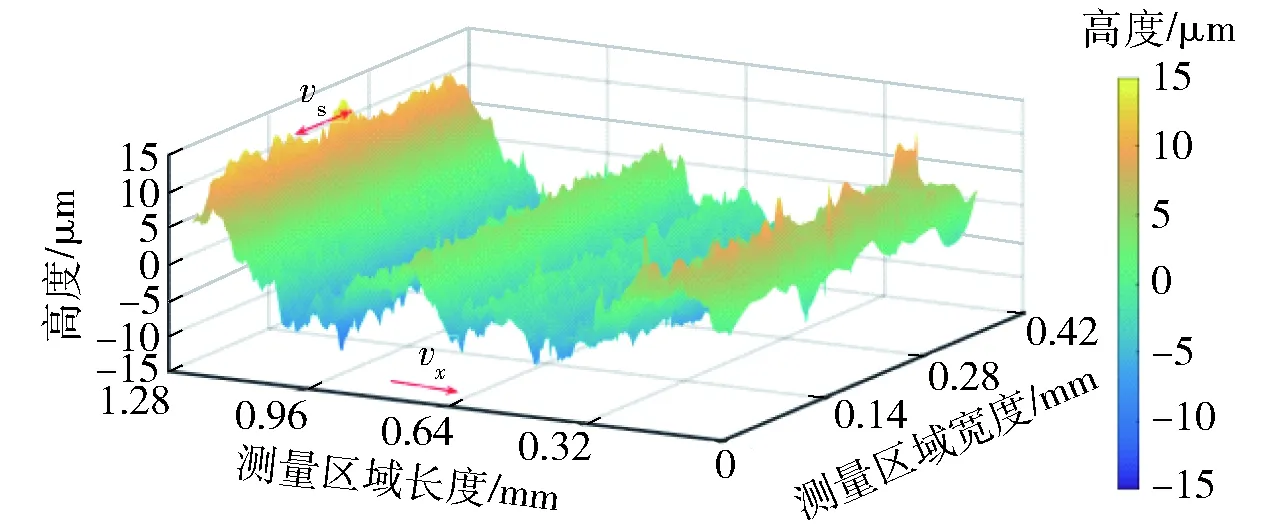
图19 线锯速度1.5 m/s的切片表面形貌图(Sa=3.87 μm)Fig.19 Surface topography with the wire saw velocity of 1.5 m/s (Sa=3.87 μm)

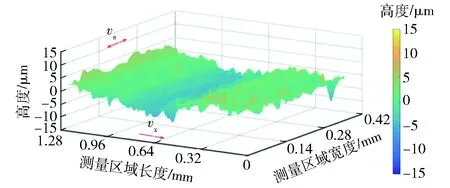
图20 参考力为1.90 N和最小方差自校正控制 的表面粗糙度图(Sa=2.51 μm)Fig.20 Surface roughness for minimum variance self-tuning adaptive control experiment for Fr=1.90 N (Sa=2.51 μm)

图21 线锯速度为2.0 m/s的切片表面形貌图(Sa=2.48 μm)Fig.21 Surface topography with the wire saw velocity of 2.0 m/s (Sa=2.48 μm)

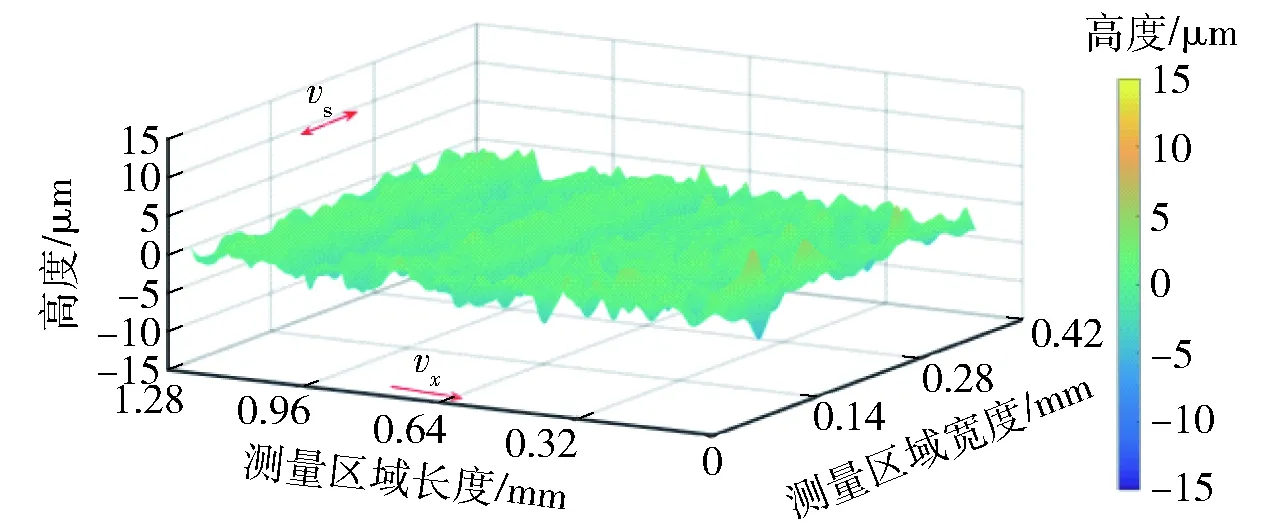
图22 参考力为1.48 N和最小方差自校正控制 的表面粗糙度图(Sa=1.55 μm)Fig.22 Surface roughness for minimum variance self-tuning adaptive control experiment for Fr=1.48 N (Sa=1.55 μm)

从以上实验结果明显可以看出：采用MVC控制器进行控制的切片其表面粗糙度比恒定参数切割的表面粗糙度小很多(粗糙度的标定尺从红色到黄色再到蓝色及黑色，表面粗糙度依次减小)，并且表面形貌也平整很多。由图17～图22中的恒定参数与加入自适应控制的切片表面形貌图可知：

1)往复式固结金刚石磨粒线锯切割机床在定参数切割加工时，切片的表面纹路较明显，表面划痕清晰可见，些许划痕有隆起，局部有少量的剥落微坑。

2)采用MVC控制器切割加工的切片表面形貌变化均匀，无明显的凹凸感，具有更好的表面状态。最小方差控制下变线锯速度切割的表面粗糙度相比于恒线锯速度的表面粗糙度值降低了28.5%～37.5%.

5 结论

为了保证往复式固结金刚石磨粒线锯切割机床在切割过程的稳定性、进一步提高切片的表面质量，本文研究了通过调节线锯速度来保持切割力恒定的方法，并将定参数切割与最小方差自适应跟踪控制切割下的表面粗糙度情况进行了对比。实验结果及数据分析表明：

1)在往复式固结金刚石磨粒线锯旋转点切割机进行定参数的切割过程中，随着切割机线锯速度的增大，切片所受的法向切割力减小，表面粗糙度减小。当线锯经过加速、匀速、减速、停顿换向、再加速、匀速、减速、停顿换向等循环过程后，其变化规律会反映在工件切割表面上，呈现出规律性的加工痕迹。

2)在原有的开放式切割平台上搭建由工控机、测力仪传感器、多功能数据采集卡以及电机调速模块等硬件模块组成的线锯运动控制平台，再辅以LabVIEW软件开发线锯速度与法向切割力的MVC，并通过线锯切割实验验证了控制器的性能。结果表明：最小方差自校正控制能够对过程模型进行在线控制，实时调节控制器的加工参数，很好地解决系统在工况下的时变问题，响应速度也较强。与定参数切割相比，采用MVC进行跟踪控制的切割能够在很大程度上减小切割力的波动，减小切片表面粗糙度，提高表面形貌的均匀度。