一道压轴试题的命题手法探究

黑龙江省伊春一中 (153000) 李翠翠福建省泉州五中 (362000) 杨苍洲

1.试题展示

(Ⅰ)求函数J1(x)与J2(x)的单调区间，并且讨论函数JK(x)的单调性；

(Ⅱ)已知m∈N+，求证：

(ⅰ)方程J2m-1(x)=1有两个根β2m-1,α2m-1；

(ⅱ)若(i)的两个根满足β2m-1>0,α2m-1<0，则β2m-1<β2m+1，α2m+1<α2m-1.

2.命题手法探究

2.1 从函数f(x)=ex的泰勒展开式说起

泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法.

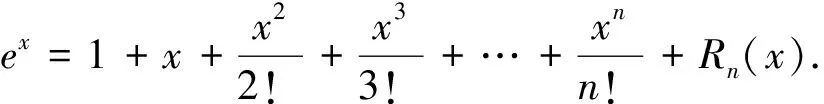
当k为奇数时，函数f(x)的图像恒在函数g(x)的图像的上方；当k为偶数时，x>0时，函数f(x)的图像恒在函数g(x)的图像的上方；x<0时，函数f(x)的图像恒在函数g(x)的图像的下方.其图像增减趋势如图1，2所示.

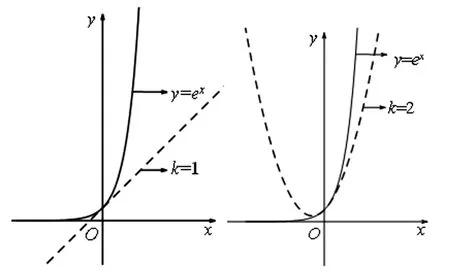
图1 图2

由此可设置试题1的问题(Ⅰ).

图3 图4

接着，我们来观察f(x)，g(x)这两个函数在x=0附近的图像.

观察得，随着k的增大，函数g(x)在x=0附近的图像总是越来越靠近函数f(x)的图像，如图5.

图5 图6

由于k取奇数和k取偶数时的函数图像有着较大的差异，为了研究的方便，为了更加直观地观察f(x)，g(x)这两个函数图像的位置关系，命题者仅研究了k为奇数的情况.此时，Jk(x)在(-∞,0)单调递减，在(0,+∞)单调递增.如图6.

如何说明函数g(x)在x=0附近的图像总是随着k的增大而越来越靠近函数f(x)的图像呢？反应在函数Jk(x)的图像中，直线y=a(a>0且a→0)与函数Jk(x)的图像在y轴两侧各有一个交点，且随着k的增大，这两个交点越来越靠近y轴.

命题者取a=1，由此可设置试题1的问题(Ⅱ).

3.试题解法探究

上述的分析都是基于图像的直观，从图像的直观观察出的函数的性质，下面我们予以证明.

问题(Ⅰ)的解答：

(3)下面用数学归纳法证明：J2m-1(x)的单调递减区间为(-∞,0)，单调递增区间为(0,+∞).

①当m=1时，命题成立；

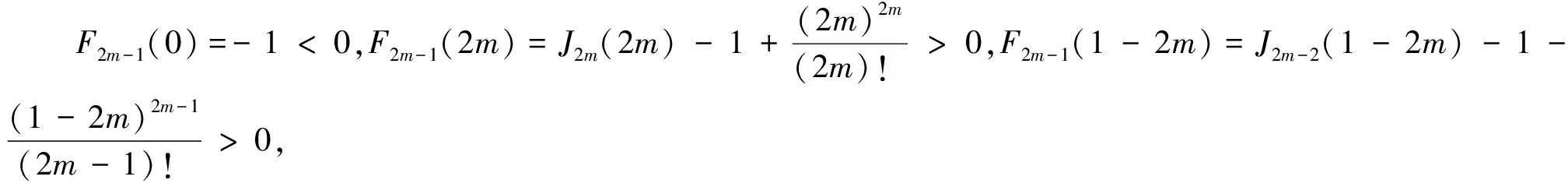
综上述，方程J2m-1(x)=1有两个根β2m-1,α2m-1.

(ⅱ)当x>0时，J2m+1(x)-J2m-1(x)=